GMOコネクトでCTOしている暗号おじさんこと菅野です。
暗号の2030年問題や暗号移行について日々情報を追っているのですが、先日、元セコム松本さんがPQC移行関連の論文が公開しているよ!と共有してくれていたので、内容を確認したのでその結果を整理するという趣旨です。
めっちゃボリュームがあったのでシリーズものになりそうな予感です。
なので、第1回としてますw
- 連載情報
はじめに
「量子計算機が現行の公開鍵暗号を破る」という話を耳にしたことがある方は多いでしょう。
しかし、それがいつ起こり、クラウド環境にどのような影響を与えるのか、そして今なにをすべきかはまだ十分に理解されていません。
本連載では、2025年発表の包括的研究論文 “Future-Proofing Cloud Security Against Quantum Attacks”(Baseri, Hafid, & Lashkari, 2025, arXiv:2509.15653v2)に基づいて 実務者の視点 から量子時代におけるクラウドセキュリティ移行を解説します。
量子計算機の脅威とは
Shor と Grover の2つの量子アルゴリズム
量子計算機が暗号に与える影響は、主に以下の2つのアルゴリズムによってもたらされます。
-
Shorのアルゴリズム(1994年)
- RSA・ECC・DHEなどの公開鍵暗号を効率的に解読可能
- 素因数分解・離散対数問題を多項式時間で解く
- 影響:現行の公開鍵暗号に根本的な安全性低下を招く
- 参考: Shor, 1997, SIAM J. Comput.
-
Groverのアルゴリズム(1996年)
- 対称鍵暗号やハッシュ関数の探索を平方根の速さに短縮
- 有効鍵長が半減(AES-256 → 約128ビット相当)
- 影響:セキュリティ強度の低下
- 参考: Grover, 1996, STOC’96
なぜクラウド環境が特に危険なのか
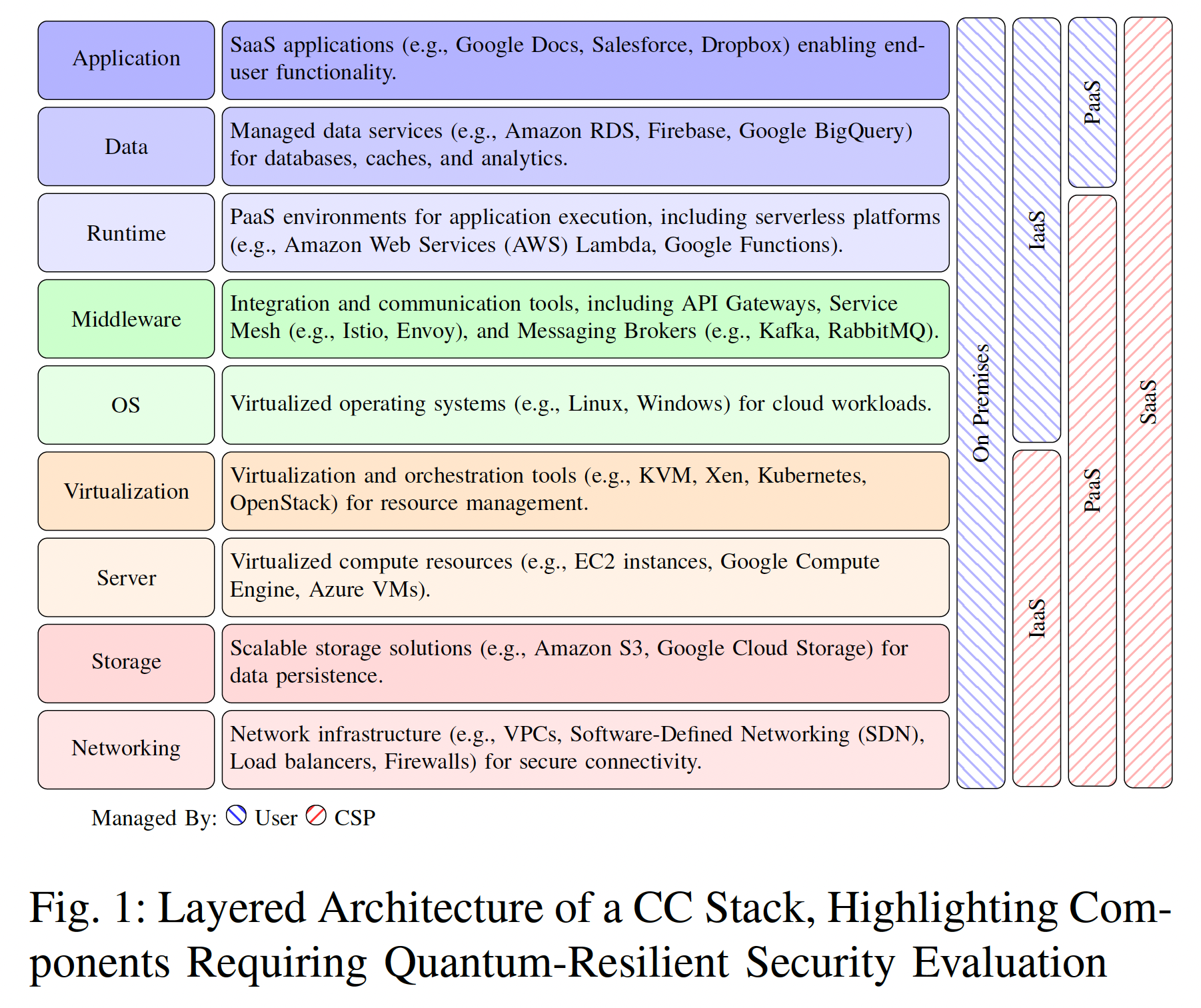
クラウドは多層アーキテクチャを持ち、各層の暗号技術が相互に依存しています。
下記の Baseri et al., 2025 Fig.1 を確認できます。
この図にあるように、ミルフィーユ上に連携していることから一箇所の暗号脆弱性が全体に波及することが伺えます。
1. PKI証明書の脆弱化 → TLS通信の信頼崩壊
PKI(公開鍵基盤)はインターネット通信の信頼の根幹です。
しかし、量子計算機によってRoot CAの署名鍵が解読されると、攻撃者は任意の証明書を発行でき、全通信が中間者攻撃の対象になります。
Root CA秘密鍵解読
↓
偽証明書発行
↓
TLS通信の完全な信頼崩壊
影響例
- HTTPS通信の盗聴(昔で言うところの「緑の鍵マーク」が付いている状態と同じで見かけ上安全)
- 偽サイトによるなりすまし
- コード署名証明書の偽造によるマルウェア配布
- オンラインバンキング・VPN・mTLS通信などへの波及
Root CAの有効期間(10〜30年)を考慮すると、2025年発行の証明書は2035〜2055年まで有効。
量子計算機がその間に実用化されれば、既存証明書はすべて危険にさらされちゃうぞということです。
2. VM移行中の暗号化脆弱性 → マルチテナント環境への波及
Baseri論文では、VM移行時の暗号化不備を「High Risk」と分類しています。
特にハイパーバイザ上で複数VMを稼働させる環境では、暗号強度の低下が横断的被害を招きます【Baseri et al., 2025, Table VIII】。
VM移行プロセスの監視
↓
暗号化されたメモリダンプ傍受
↓
量子計算機で鍵を復元
↓
他テナントVMへの横展開
- リスク:情報開示・改ざん(STRIDE分類)
- 要因:VM Migration時の暗号化不完全性、共有キャッシュ経由のサイドチャネル
- 対策:PQCベースのハイパーバイザ鍵管理、暗号鍵の頻繁なローテーション
3. APIキーの推測・解読 → サービス間連鎖侵害
マイクロサービス間ではAPIキーを用いた認証が多数存在します。
Groverのアルゴリズムにより、探索空間が平方根的に削減されることで、AES-128相当のAPIキーも理論上突破が容易になります。
1つのAPIキー漏えい
→ 認証連鎖を経由し別サービスへ侵入
→ DBや決済APIに波及
Baseri論文ではこれを
“Quantum-Enhanced API Abuse / API Key Leakage” と分類し、STRIDEで「Spoofing」「Tampering」「Elevation of Privilege」に該当すると分析しています。
影響例
- 金融SaaSでの不正送金
- CI/CDパイプライン改ざん(GitHub/GitLabキー)
- クラウド管理APIを通じた全インフラ侵害
15年タイムライン:「今」が対策の臨界点
Global Risk Institute の専門家調査によれば(Baseri論文 Fig.6 引用)、RSA-2048を24時間以内に破壊できる確率は以下の通りです。
| 期間 | 破壊確率 |
|---|---|
| 5年以内 | 約5% |
| 10年以内 | 約22% |
| 15年以内 | 約44% |
| 20年以内 | 約67% |
| 30年以内 | 約82% |
この論文では「15年を標準的リスク評価期間」として採用しています。
したがって、2035年前後を見据えた移行計画 が求められることを意味しており、各国政府機関のPQC移行の期限ともあってますね!
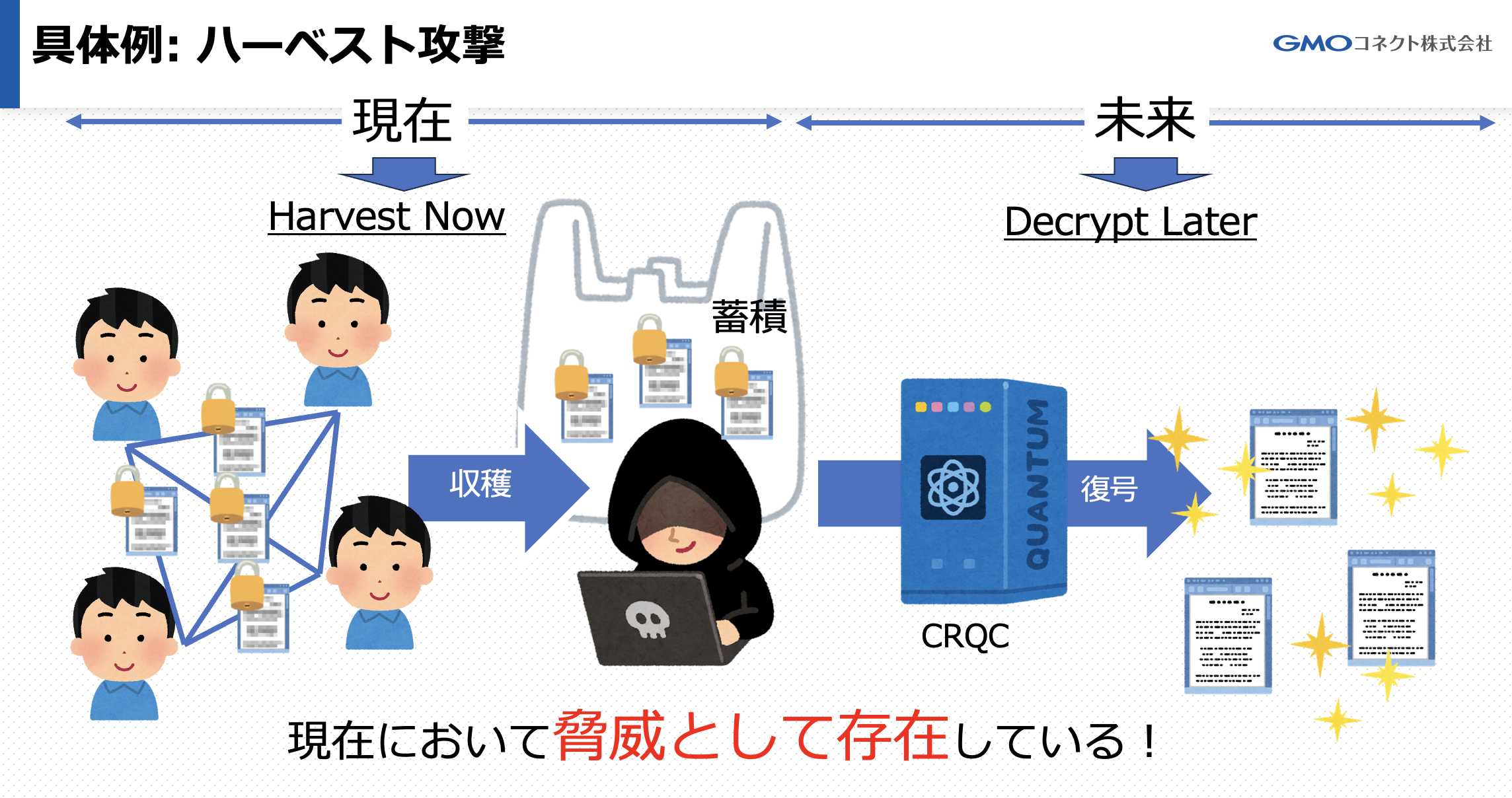
Harvest Now, Decrypt Later(HNDL)攻撃
今暗号化されたデータを保存し、将来量子計算機で解読するという攻撃です。
図で表してみると以下のような感じです。
具体的な年数を入れると、よりグッと来ますね。
現在(2025) 将来(2035〜2040)
暗号化データ → 保存 → 量子計算機で解読
このことから、長期秘匿が必要な情報(医療・政府・企業知財)は、今すぐPQCへの移行が必須ということになります。
クラウド事業者の現状
主要クラウド事業者の量子耐性対応(論文および各社技術ブログ参照):
| プロバイダ | 主な対応 (2024–2025) |
|---|---|
| AWS | ML-KEM (Kyber) ハイブリッドTLS, KMS/ACM対応, PQC鍵管理強化 |
| Google Cloud | ChromeでML-KEMハイブリッドHTTPSを標準化、Cloud KMSでPQC署名を試験提供 |
| Microsoft Azure | SymCryptにML-KEM, ML-DSA, SLH-DSA実装、2033年までの全面対応を目標 |
(出典: Baseri et al., 2025, Section VIII; 各社公式ブログ)
移行の3フェーズ(Baseri et al., 2025, Section VI)
Phase 1: Pre-Transition
├─ 古典暗号資産の棚卸し (Crypto Inventory)
└─ 長期秘匿データの特定
Phase 2: Hybrid Transition
├─ PQC + 現行暗号の併用
├─ 後方互換性維持
└─ 段階的移行
Phase 3: Post-Transition
├─ 完全PQC化
└─ 継続的モニタリングと暗号更新
この論文では、Phase2としてPQ/Tハイブリッド構成を置いていますが、昨今の世の中を見ていると・・・ハイブリッド構成を経由せずにPure PQCへの移行を目指しているのかな?と感じることが多いです。
どうなるか時代が証明してくれると思いますが。
次回予告
第2回では、実務者のためのリスク評価フレームワーク を解説します。
- STRIDEモデルを量子脅威に適用する方法
- Likelihood(発生可能性)と Impact(影響度)の具体的評価
- Crypto Inventory(暗号資産の棚卸し) の実施手順
- あなたのシステムの量子リスクスコアを算出する方法
実際に使える「量子時代のリスク評価」に関する情報を整理します。
まとめ
- 量子計算機(CRQC)による暗号脆弱化は15年以内に現実的脅威として予想されている
- 備えあれば憂いなしの精神ですね
- クラウドは多層構造のため、連鎖的影響が発生しまう脅威があるので注意
- PKI脆弱化 → TLS通信全体が危険に
- VM移行中の暗号化不備 → マルチテナント被害
- APIキー推測 → サービス間連鎖侵害
- HNDL攻撃により、今のデータが将来解読されるリスクは存在している
- 各クラウド事業者はすでにPQC移行に取り組みつつある
- ハイブリッド移行戦略が推奨される
「まだ先の話」ではなく、今始めるべきクラウドセキュリティ課題です。
参考文献
- Baseri, Y., Hafid, A., & Lashkari, A. H. (2025). Future-Proofing Cloud Security Against Quantum Attacks: Risk, Transition, and Mitigation Strategies. arXiv:2509.15653v2
- Global Risk Institute (2022). Quantum Threat Timeline Report
- NIST (2024). Post-Quantum Cryptography Standards (FIPS 203, 204, 205) — https://csrc.nist.gov/projects/post-quantum-cryptography
- P. W. Shor (1997). Polynomial-Time Algorithms for Prime Factorization and Discrete Logarithms on a Quantum Computer. SIAM J. Comput., 26(5), 1484–1509. DOI: 10.1137/S0097539795293172
- L. K. Grover (1996). A Fast Quantum Mechanical Algorithm for Database Search. STOC’96 Proceedings, pp. 212–219. DOI: 10.1145/237814.237866
最後に、GMOコネクトでは研究開発や国際標準化に関する支援や技術検証をはじめ、幅広い支援を行っておりますので、何かありましたらお気軽にお問合せください。