Go to Qiita Advent Calendar Top
LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@sato_ryo

ABC421_解法メモ(Python)

Last updated at Posted at 2025-08-30

はじめに

気になった問題について、自分の考え方や実装方法をまとめます。

C - Alternated

問題

ABC421 C - Alternated

"A" と "B" がそれぞれ N 個ずつ含まれる文字列 S が与えられます。
隣り合う文字を交換していくことで、A と B が交互に並ぶ文字列を作る場合の 最小移動回数 を求める問題です。

例

文字列 AAABBB の場合：

AAABBB → AABABB → ABAABB → ABABAB

と 3 回移動するのが最小です。
よって出力は 3 です。

考え方

1. 最終文字列のパターン

最終的に作れる文字列は次の2パターンです：

  1. ABABAB...（A が偶数番目に入るパターン）
  2. BABABA...（A が奇数番目に入るパターン）

どちらかの文字列にするための最小移動回数の 小さい方 が答えになります。

2. 各 A の最適な割り当て

  • 初期位置が左から順に A を、最終的な目標位置の左から順に割り当てるのが最適です。
  • 理由：順序を入れ替えて割り当てると無駄な移動が発生するからです。

例）

初期: A1 A2
最終: 位置2 位置1 に移動しようとすると余計な移動が必要になる

↓ 多少手抜きですが、Google AI Studioのnano bananaで画像を作ってもらいました。
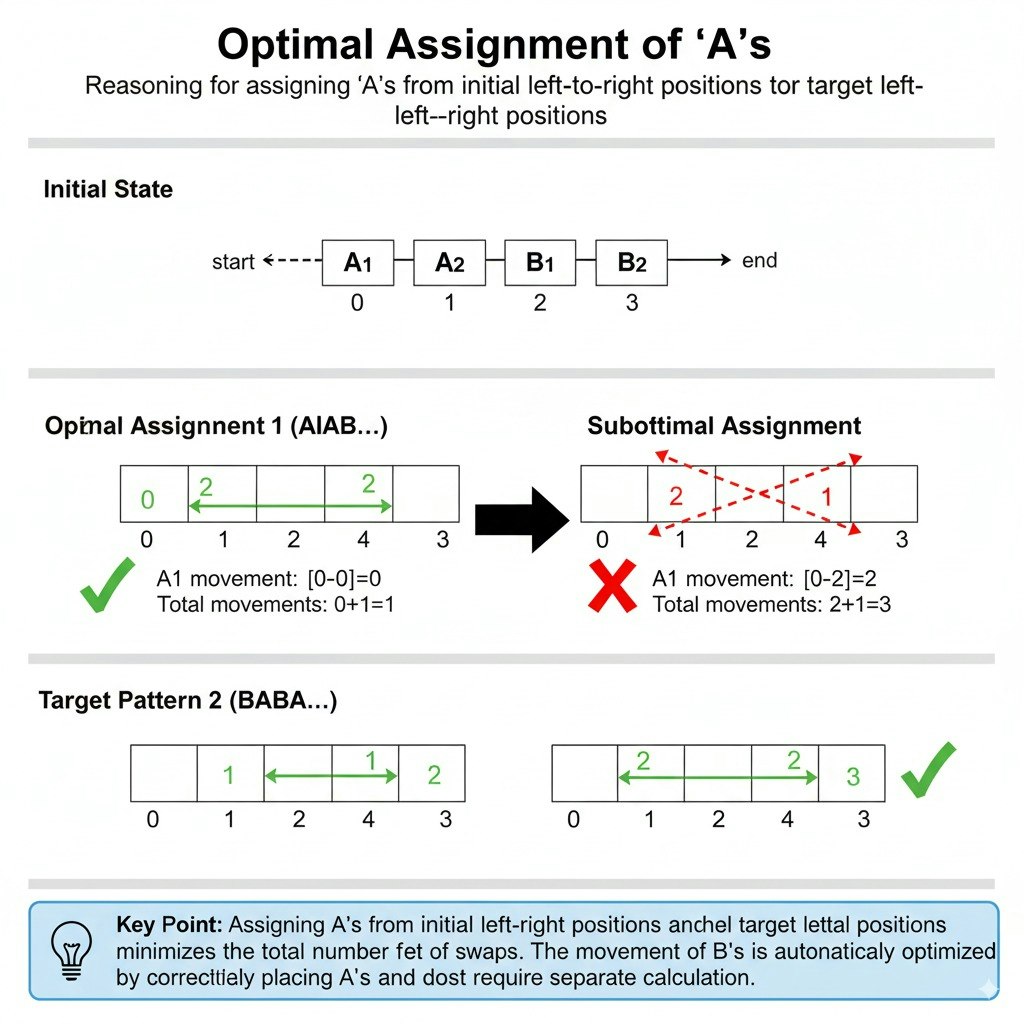
Generated Image August 31, 2025 - 12_27AM.jpeg

3. 移動コストの計算

  • 隣接スワップしかできないため、各 A の初期位置から理想位置までの距離 = 最小移動回数 になります。
  • 1 回の移動で他の A の移動回数を減らしたり増やしたりすることはできないので、各 A の移動回数を合計すれば最小総移動回数が求まります。

4. B について

  • B も交互に並べる必要がありますが、A を正しく配置すれば B は自動的に最適な位置に揃う ため、別途計算する必要はありません。

5. アルゴリズムの手順

  1. A の位置をリストに格納する
  2. ABAB... と BABABA... それぞれで、各 A の理想位置との差（絶対値）の合計を計算
    1. の小さい方が答え

6. Python 実装例

n = int(input())
s = input()

# A の初期位置を取得
aPos = [i for i, c in enumerate(s) if c == "A"]

# ABAB... と BABABA... の理想位置との差分合計
cost1 = sum(abs(aPos[i] - 2*i)   for i in range(n))
cost2 = sum(abs(aPos[i] - (2*i+1)) for i in range(n))

print(min(cost1, cost2))

💡 ポイント

  • 隣接 swap の最小回数 = 転倒数 (inversion number)
  • A を順番通りに左から目標位置に割り当てるだけで最小化できる
  • B の動きは自動的に最適化される

補足: 転倒数について

転倒数（inversion number）とは、数列や順列において、本来あるべき順序と逆になっている要素のペアの数のことです。隣接する要素をスワップする操作は、転倒数をちょうど1つ減らします。したがって、隣接スワップで目的の順列（この問題では ABAB... や BABA...）にするための最小移動回数は、現在の順列の転倒数に等しくなります。

なぜ転倒数が最小移動回数なのか？

隣接スワップは、隣り合う要素の位置を交換する操作です。この操作は、他のどの要素の相対的な順序にも影響を与えません。これにより、転倒数を1つずつ確実に減らすことができます。目的の順列は転倒数が0の状態なので、現在の転倒数と同じ回数だけスワップを行えば、必ず目的の形にすることができます。

今回の問題では、元の文字列 S から A だけを取り出し、その相対的な位置関係を考えます。
例えば、S = "AAABBB" の場合、A の初期位置は 0, 1, 2 です。

目標の文字列が ABABAB の場合、A は位置 0, 2, 4 にあるべきです。
このとき、それぞれの A がどの A に対応するかを考えます。

  • 初期位置 0 の A → 目標位置 0 の A
  • 初期位置 1 の A → 目標位置 2 の A
  • 初期位置 2 の A → 目標位置 4 の A

このように、初期位置が左から順番に、目標位置も左から順番に対応させるのが最適です。そのように対応付けたときに、各 A が移動すべき距離の合計が最小になり、それが転倒数と一致します。

各 A の初期位置と理想位置の差の絶対値の合計は、その A を目標位置に移動させるために必要な隣接スワップの回数を示します。すべての A の移動回数の合計が、文字列全体を理想的な形にするために必要な最小移動回数、すなわち転倒数に他なりません。

D - RLE Moving

問題

ABC421 D - RLE Moving

高橋君と青木君が無限に広いグリッド上で移動します。
二人は同時に1マスずつ、上下左右のいずれかの方向に移動します。
高橋君と青木君の座標が一致する回数を求める問題です。
各移動は移動方向(UDLR)と進む距離の組で与えられます。（ランレングスエンコーディング形式）。

制約

  • 初期座標 (Rt, Ct), (Ra, Ca) は -10^9 から 10^9
  • 総移動回数 N は 10^14
  • ランレングスエンコーディングの区切り数 M, L は 10^5
  • 各移動の距離 Ai, Bi は 10^9
  • N = ΣAi = ΣBi

考え方

N が非常に大きいため、愚直に N 回の移動をシミュレーションすることはできません。しかし、移動の指示がランレングスエンコーディングで与えられることを利用すると、効率的にシミュレーションできます。

ブロックごとの処理

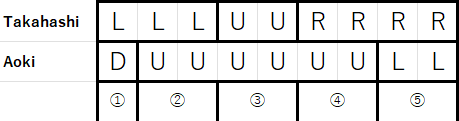
高橋君と青木君の移動方向が切り替わるタイミングごとに区間を「ブロック」として捉え、そのブロック内で二人が衝突するかどうかを考えます。

イメージ図

この説明は解説がかなりわかりやすいです。

(下記、↑の解説の画像です。)
解説から拝借

具体的には、高橋君と青木君が現在の進行方向でそれぞれどこまで進めるかを保持します（zan_t, zan_a）。この zan_t と zan_a の小さい方、つまり両者が同じ進行方向を維持できる期間を1ブロックとして処理を進めます。
このように、min(zan_t, zan_a) を k とし、k 回の移動を一つのブロックとしてまとめて処理します。

各ブロック内での衝突判定

1ブロック（k 回の移動）内で、高橋君と青木君が衝突するかどうかは、二人の進行方向によって以下の3つのケースに分けられます。

1. 高橋君と青木君の進行方向が同じ場合

この場合、高橋君と青木君は同じ速さで同じ方向に進みます。したがって、最初に二人の座標が一致していれば、そのブロックの k 回の移動中ずっと衝突し続けます（一体となって動く）。それ以外の場合は衝突しません。
衝突回数は k 回です。

2. 高橋君と青木君の進行方向が逆方向の場合（例: 高橋君が'U'、青木君が'D'）

この場合、同じ軸上（垂直方向または水平方向）で互いに向かい合って進んでいます。衝突するためには、以下の条件を満たす必要があります。

  • 移動しない方向の座標が一致していること: 例えば、垂直方向の移動であれば、横方向の座標が一致している必要があります。
  • 座標の差が偶数であること: 高橋君と青木君は1回の移動で合計2マスずつ距離が縮まります。移動直後に一致するためには、初期の座標差が偶数でなければなりません。
  • 座標差が狭まる方向であること: 距離が広がる場合は衝突しません。
  • 座標差 / 2 がブロック内で収まること: 衝突するまでに必要な移動回数が k 回以内でなければなりません。

これらの条件を全て満たす場合、このブロック内でちょうど1回だけ衝突します。

3. 高橋君と青木君の進行方向が縦横バラバラの場合（例: 高橋君が'U'、青木君が'R'）

この場合、二人の相対的な位置関係を考慮します。高橋君から見た青木君の相対座標 (diff_r, diff_c) と、高橋君から見た青木君の相対移動ベクトル (diff_dir_r, diff_dir_c) を考えます。

衝突するためには、m 回移動後に相対座標が (0,0) になる必要があります。つまり、diff_r + m * diff_dir_r = 0 かつ diff_c + m * diff_dir_c = 0 となる m が存在し、それが 1 <= m <= k の範囲内にある必要があります。

具体的には、
m = -diff_r / diff_dir_r
m = -diff_c / diff_dir_c
これら2つの m が一致し、かつ 1 <= m <= k を満たす場合に1回だけ衝突します。

シミュレーションの継続

上記ブロックごとの処理を、高橋君と青木君の全ての移動指示が終わるまで繰り返します。計算量は、M と L の合計回数（最大 10^5）を繰り返すため、O(M+L) となり、十分高速に動作します。

実装

上記考え方を元にPythonで実装したコードです。

#!/usr/bin/env python3
r_t,c_t,r_a,c_a = map(int,input().split())
# 方向を座標変化量に変換する辞書
d = {'U':(-1, 0),'D':(1, 0),'L':(0, -1),'R':(0, 1)}
n,m,l = map(int,input().split())
s_a_m = [] # 高橋君の移動指示
for _ in range(m):
    s, a = input().split()
    s_a_m.append((s, int(a)))
t_b_l = [] # 青木君の移動指示
for _ in range(l):
    t, b = input().split()
    t_b_l.append((t, int(b)))

# 現在処理中の移動指示のインデックス
t_cnt,a_cnt = 0,0
# 現在の移動指示で残りの移動回数
zan_t,zan_a = s_a_m[0][1],t_b_l[0][1]
# 現在の移動方向
dir_t,dir_a = d[s_a_m[0][0]],d[t_b_l[0][0]]
# 現在の座標
r_t_now, c_t_now, r_a_now, c_a_now = r_t, c_t, r_a, c_a 
ans = 0

# どちらかの移動指示がなくなるまでループ
while t_cnt < m and a_cnt < l:
    # 共通して進める移動回数
    k = min(zan_t, zan_a) 
    
    # 青木君から高橋君への相対座標 (青木君 - 高橋君)
    diff_r_now, diff_c_now = r_a_now - r_t_now, c_a_now - c_t_now
    # 青木君から高橋君への相対移動方向 (青木君の方向 - 高橋君の方向)
    # 1回の移動で相対座標がどれだけ変化するか
    diff_dir_r, diff_dir_c = dir_a[0] - dir_t[0], dir_a[1] - dir_t[1]

    # ケース1: 相対移動方向がゼロ (両者が同じ方向へ同じ速さで進む)
    if diff_dir_r == 0 and diff_dir_c == 0:
        # 初期座標が一致していれば、ブロック全体で衝突し続ける
        if diff_r_now == 0 and diff_c_now == 0:
            ans += k
    # ケース2: 縦方向のみに相対移動がある (横方向の相対移動はなし)
    elif diff_dir_r == 0:
        # 縦方向の座標差がゼロで、横方向の相対移動で衝突する場合
        if diff_r_now == 0 and (-diff_c_now) % diff_dir_c == 0:
            # 衝突するまでの移動回数を計算
            # -diff_c_now は t回目の移動で青木君が目標とする相対C座標
            # diff_dir_c は 1回の移動での相対C座標の変化量
            # 例: diff_c_now=4, diff_dir_c=2 なら 4/2 = 2回後に衝突
            collision_time = (-diff_c_now) // diff_dir_c
            # 衝突がブロック内で発生し、かつ1回以上の移動後である場合
            if 1 <= collision_time <= k:
                ans += 1
    # ケース3: 横方向のみに相対移動がある (縦方向の相対移動はなし)
    elif diff_dir_c == 0:
        # 横方向の座標差がゼロで、縦方向の相対移動で衝突する場合
        if diff_c_now == 0 and (-diff_r_now) % diff_dir_r == 0:
            collision_time = (-diff_r_now) // diff_dir_r
            if 1 <= collision_time <= k:
                ans += 1
    # ケース4: 両方の軸方向に相対移動がある
    # 衝突するためには、縦と横の衝突までの移動回数が一致する必要がある
    # また、それぞれの軸で割り切れる必要がある
    elif (-diff_r_now) % diff_dir_r == 0 and (-diff_c_now) % diff_dir_c == 0:
        collision_time_r = (-diff_r_now) // diff_dir_r
        collision_time_c = (-diff_c_now) // diff_dir_c
        # 縦と横の衝突時間が一致し、かつブロック内で衝突する場合
        if collision_time_r == collision_time_c and 1 <= collision_time_c <= k:
            ans += 1


    # k回移動後の座標を更新
    r_t_now += dir_t[0] * k
    c_t_now += dir_t[1] * k
    r_a_now += dir_a[0] * k
    c_a_now += dir_a[1] * k

    # 残りの移動回数を更新
    zan_t -= k
    zan_a -= k
    
    # 高橋君の移動指示が完了した場合、次の指示に進む
    if zan_t == 0:
        t_cnt += 1
        if t_cnt < m:
            dir_t = d[s_a_m[t_cnt][0]]
            zan_t = s_a_m[t_cnt][1]
    # 青木君の移動指示が完了した場合、次の指示に進む
    if zan_a == 0:
        a_cnt += 1
        if a_cnt < l:
            dir_a = d[t_b_l[a_cnt][0]]
            zan_a = t_b_l[a_cnt][1]

print(ans)

まとめ

この問題では、N が大きい場合のシミュレーションを、ランレングスエンコーディングされた移動指示を利用して効率的に行うことが重要です。高橋君の移動方向が同じ区間の分割と、青木君の移動方向が同じ区間の分割を合わせた分割を「ブロック」としてまとめ、各ブロック内で相対座標と相対移動ベクトルを考慮して衝突回数を計算することで、O(M+L) の計算量で問題を解くことができます。

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?