はじめに
この記事は「PERSOL PROCESS & TECHNOLOGY Advent Calendar 2020」の13日目の記事になります。
私は三回目の登場です。今年のアドカレMVPは頂きます。
素敵な先輩方と同期が素敵な記事をたくさん書かれているので、是非他もご覧になってみてください。
なろう読んでたら遅れました。ごめんなさい......。
概要
この記事の第一の目的は「競技プログラミングはアルゴリズムを暗記するだけ」「C++以外ではできない」「役には立たない」といった偏見を打破することです(最後は一部否定できませんが...)。
このような出所もよくわからない奇妙な偏見を聞きかじって二の足を踏んでいる方が、弊社でも少なからずいらっしゃることに気づきました。
よって、AtCoderで出題されるような競技プログラミングの問題は、本質的に何を問うているのかという話からしていきます。
私が入社して以来ずっと競技プログラミングを布教しているにも関わらず中々成果が上がっていないのですが、この機会に正しい情報を伝えることが出来れば、弊社にerがもっと増えればいいなと期待してこの記事を書いています。
競技プログラミングを既にやっている人にはあまり面白みのない記事(緑以上の人には何ら得るものがないと思います)なので、その旨ご承知おきください。
導入
突然ですが、今お使いのPCが一秒間に何回の計算を処理出来るかご存じですか?
言語にもよりますし、CPUなどの性能にも大きく左右されますが概ね$ 10^9 $回程度です。日本人が直感的に理解できる体系に即して言うと10億回程度となります。
これを多いと感じるか少ないと感じるかは人によるかと思いますが、競技プログラミングをやっている人間で多いと感じる人間は恐らくいないと思います。
というのも、競技プログラミングで出題される問題の多くは、普通にやっては計算回数が10億回を大きく超えてしまうような(とても数秒では終わらない)タスクを、如何にして数秒以内に処理できるように落とし込むかを問うものになっています。
とても制限時間内に解けそうにないように見える問題を鮮やかな手法で、まるで魔法のように解く。その面白さに魅せられて、またそんなことが出来る上級者に憧れて、私は競技プログラミングを続けています。他の多くの人も、大なり小なりこのような思いを持って日々精進していると思います。
というわけで私が特に魔法のようだと感動した問題とアルゴリズムについて解説しつつ、競技プログラミングとはどのようなものか、どの程度役に立つものかについて以下書き連ねようと思います。
ちなみに言語についてはもうここで言ってしまいますが、大抵のAtCoderの問題では(CodeforcesとかJOIとかは知りません)想定計算量は多くとも$ 10^7 $程度であって、pythonでも十分に計算が終わるように調整されています。
Red Coder(2020/12/14現在で日本に33人しかいない最強存在)でもPythonのみで戦っておられる方がおられるので、赤になることすらやってやれないことは証明されています。
また青葉山のなろうオタク最強エースのようにAwkでコードゴルフがてら1200問以上通している人もいますし、大学の後輩にbrainf*ck縛りで茶色まで到達したヤバい人もいます。
言語に関してはむしろ相当な自由度があると思って良く、勉強中の言語のちょっとしたならし等にも積極的に使っていけるようになっています。
今回の問題に使うアルゴリズム
前提知識として、二分探索について説明します。この世で最も強力なアルゴリズムの一つでしょう。
初心者にもわかりやすく、威力も抜群という花形アルゴリズムです。
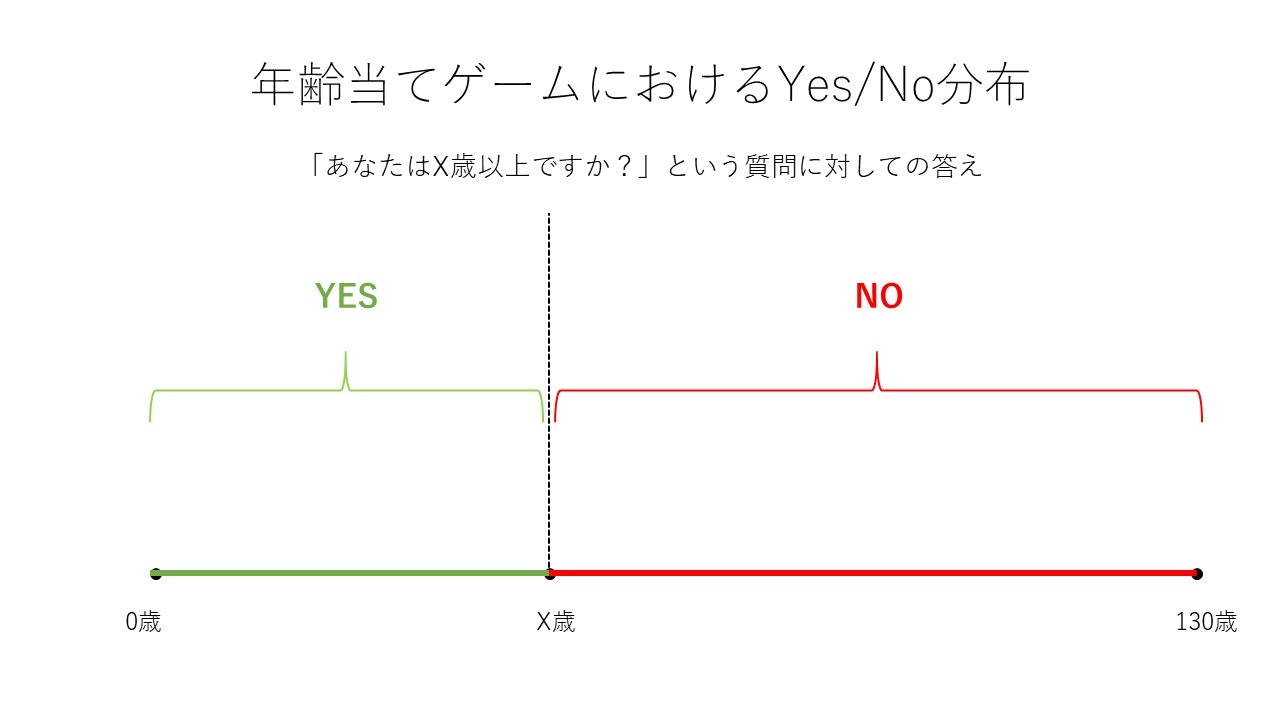
わかりやすく説明されているものとしてけんちょんさんのこの記事の年齢当てゲームのところを読んでみてください。大体イメージがつくと思います(けんちょんさんは偉大ですね......)。
さて、私もこの年齢当てゲームを例にとって説明させていただきます。
ある人の年齢を知りたい時、まず思いつくのは「あり得る答えをすべて聞く」ことです。極端な話、128歳くらいまで生きている人はいなさそうなので、0歳から127歳まで一つ一つ聞いていけばやがて答えに辿り着きます。
しかしこれでは人が長生きであったときに困ってしまいます。仮に人が$ 10^9 $歳まで生きるようになっては大変です。0歳から順に聞いていっては、年齢を当てるまでに更に100歳ほど歳を取ってしまうことでしょう。
これはあまりにも融通がきかない話に聞こえるかもしれませんが、コンピューターはこんなものです。人間にとってそれがどんなに面倒でも、機械は指示されたことを愚直に行い続けます。だからこそ人間が賢いアルゴリズムを与えてやる必要があるのです。
というわけで賢いアルゴリズムである二分探索を適用してみます。
まず人間が127歳まで生きるとして$ 127 $の半分、$ 64 $について「あなたは64歳以上ですか?」と聞き、回答を得ます。
お分かりいただけましたか?実は今の時点で探索範囲が半減しています。
今の問いについてYesであれば、その人は0歳以上64歳未満です。Noであれば64歳以上128歳未満です。
これを続けます。回答をYesとして$ 64 $の半分、$ 32 $について「あなたは32歳以上ですか?」と聞き、回答を得ます。この時探索範囲がまた半減します。
これを繰り返すと、一つの質問ごとに探索範囲が$ 1/2 $されていくため、必ず答えは一つに収束します。そしてこの収束するために要するステップ数は全探索範囲を$X$とすると**$ \log_{2} X $**に一致します。
数式で見るとピンと来ないかもしれませんが、これはハチャメチャにヤバい事実です。
計算してみましょう。今の年齢当てゲームだと全探索範囲Xは$ X = 127-0+1 $として$128$です。そして$ \log_{2} X $とは$ 2 $を何乗するとXになるのかというものを表すものですから$ 128 = 2^7 $なので$ \log_{2} 128 = 7$となります。
つまり探索範囲128の年齢当てゲームは最大でも7回の質問で答えを出せるということになります。一つ一つ全ての年齢を聞いていく手法より18倍程度高速です。すごいですね。
では探索範囲が$ 10^9 $ではどうなるでしょうか?128が7になったから、10億が5千万くらいにはなる?計算してみましょう。
$ \log{2} 1000000000 = 29.8973528... $
はい。30にすら届きません。参考までに$ 2^{30} = 1073741824$です。
10億回が29回に圧縮されてしまいました。人力でも何とかなりそうなレベルですね。
とまあこのように、二分探索は探索範囲の増加にめっぽう強いアルゴリズムです。小学生大好き無量大数すら平気で扱うことができます。
しかしこれを見て「こんなすごいものがあるならあんな問題が解けるじゃん!」と瞬時に思いつける方はどれくらいおられるでしょうか。
「すごいのはわかったけど、人間は10億歳まで生きないし、どこで活かせるのかよくわからないよね。非実用的とまでは言わないけど、実際使えるところは限られるんじゃない?」と考える人の方が多いと思います。
しかしそれは否です。この二分探索、とんでもなく汎用的です。「そんなことにまで活かせるの!?」と驚くこと請け合いです。
というわけで、私が出会ったときに感動した問題を紹介します。
億マス計算
元ネタはAtCoderのこの問題です。
問題概要はこんな感じです↓ 元の問題のサンプルを見るとより理解が深まるでしょう。
長さNの数列Aと数列Bが与えられる。百マス計算のようにそれぞれの数列が縦横に並んでいるので、その積を全て求めたときの小さい方からK番目の数を答えよ
非常にシンプルというか、プログラミングの練習問題くらいの問題設定のように見えます。よって、簡単じゃないか?という風に感じるのは自然です。
要は数列の全ての組み合わせに対して積を求めて小さい順にK番目の数を出してやれば良いので、
vector<long long> ans;
// 全ての組み合わせに対して積を求める
for (int i = 0; i < N; ++i) {
for (int j = 0; j < N; ++j) {
long long tmp = A[i] * B[j];
ans.push_back(tmp);
}
}
// 小さい順にソートしてk番目の値を出す
sort(ans.begin(), ans.end());
cout << ans[k-1] << endl;
こういうコードが考えつくと思います。実際にNが小さければこれでも解けます。
しかし$ N \leq 10^5 $であればどうでしょうか(元の問題では$ N \leq 30000 $です)。どのくらいの回数計算が行われるか考えてみましょう。
まず目につくのは全ての組み合わせに対して積を求めているパートです。これは内側のループがN回処理を終えた後に、外側のループが1回進むという形になっています。
つまり$ N \times N $回の計算が行われることになります。よって$ 10^5 \times 10^5 = 10^{10} $です。
更にソートをしています。数列のソートに必要な計算量は、数列の要素数を$ X $として$ O(X \log X) $です。今回$ X = 10^{10} $であり$ \log_{2} 10^{10} = 33.219280... $なので、全体で$ 3 \times 10^{11} $くらいの計算が必要になります(実際は入力の受け取りなども必要なのでもう少しかかります)。
さて、一般のPCでは1秒間に$ 10^9 $くらいの処理が出来ると前述しました。今の計算量だと、大体五分から十分程度はかかることになります。これではとても制限時間の二秒には間に合いません。
そして今回の場合深刻なのはメモリの使用量です。今回の制約だと各数字は$ 10^9 $まであり得るので、それの積を取るとなると64bit整数を使う必要があります。そしてその数列の要素数は$ 10^{10} $です。
100億個の64bit整数値データを保存するとどのくらいメモリを使うのか計算してみてください。私は計算するのが面倒だったのでうしさんに聞いてみましたが、大体76GBくらいだそうです。
今目の前にあるPCは76GB以上メモリを積んでいます!という方はどのくらいおられるのでしょうか。多くはないでしょう。はっきり言ってこの計算のためにそれだけメモリを確保するのは中々馬鹿げています。
というわけで、全ての組み合わせに対して積を求める方針では解くことができないということがわかりました。
しかしこの問題はこれくらいしかやり方がないように感じられると思います。「どう考えても全ての積を求めないと小さい方からK番目の値なんて出しようがないじゃないか」と考えられているかもしれません。
では、これを二分探索という魔法のようなアルゴリズムで劇的に高速化/省メモリ化していきましょう。
二分探索解
二分探索はどのような問題に適用できるか、その条件を考えてみます。
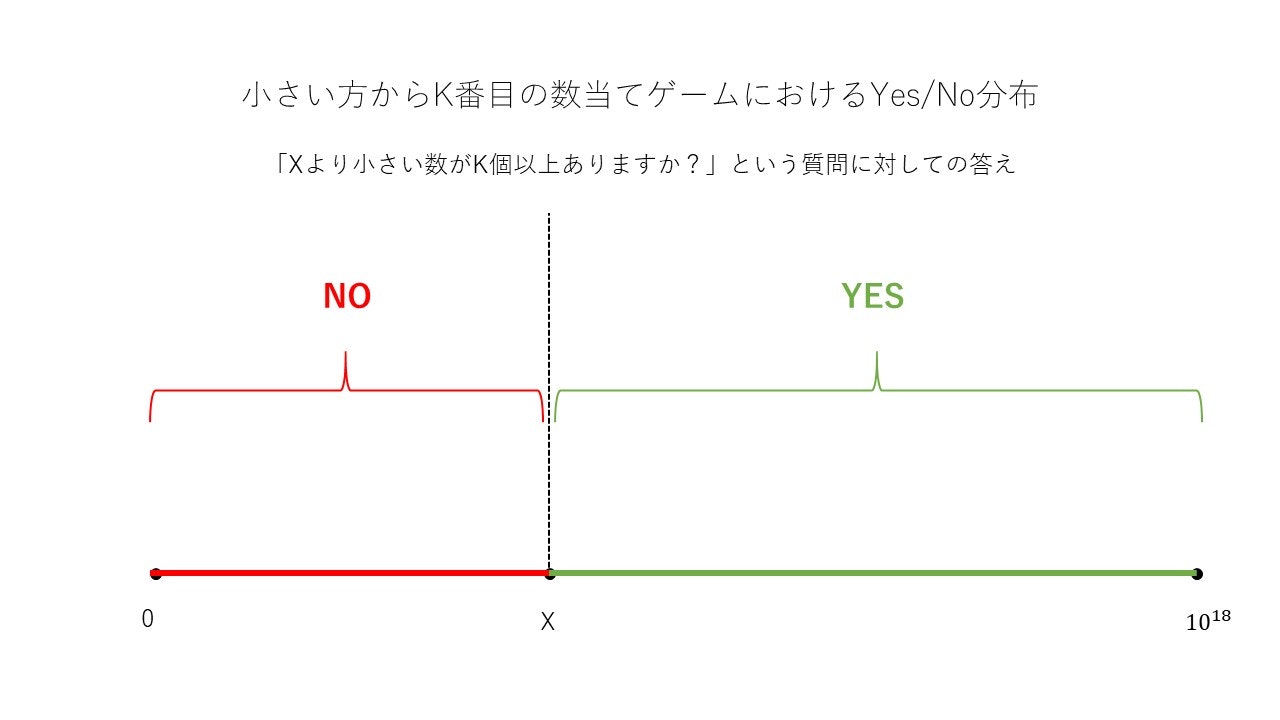
以下図の通り先ほどの年齢当てゲームでは、ある一つの点(その人の年齢)を境に、YesとNoの分布が綺麗に分かれています。
ある一点までは最初から全てYes(またはNo)であり、ある一点から最後までは全てNo(またはYes)となっています。この性質を単調性と呼び、探索空間がこの性質を満たしている時に限り二分探索が適用できます。
つまり、このような単調性を問題の中に見つけることが出来れば、二分探索で解くことが出来るということです。
この問題ではどのような場所に単調性を見出すことができるでしょうか。閃いた方がいるかもしれません。少し難しいので、これを自力で閃くことが出来たのならば競技プログラミングの素質があることは間違いありません。
先ほどは「年齢当てゲーム」でした。それを「小さい方からK番目の数当てゲーム」に言い換えて考えてみます。
「年齢当てゲーム」での質問は「あなたはX歳以上ですか?」でしたから、これも言い換えてみましょう。ここが肝です。**「Xより小さい数(X以下の数)がK個以上ありますか?」**としてみましょう。
すると以下図のように単調性が得られます。
試しに小さいケースで実験してみましょう。
$ N = 3, K = 4, A = {7, 6, 5}, B = {9, 6, 1} $とします。全ての積は$ C = {5, 6, 7, 30, 36, 42, 45, 54, 63} $となって、その四番目なので答えは30です。
この30という数字を「Xより小さい数(X以下の数)がK個以上ありますか?」という質問を繰り返して当ててみます。
- 答えのあり得る範囲を雑に1から100と見積もって$ X = 50 $からスタートします。「50以下の数が4個以上ありますか?」という質問です。7個あるのでYesとなります。
- 50がYesだったので、50より大きい数については考えずとも良くなりました。よって次は$ X = 25 $となります。「25以下の数が4個以上ありますか?」3つしかないのでNoです。
- 25がNoだったので、単調性の境目は25から50の間のどこかとなります。次は$ X = (50+25)/2 = 37 $です。「37以下の数が4個以上ありますか?」5つあるのでYesです。
- 範囲は25から37の間に絞られました。次は$ X = (25+37)/2 = 31 $です。「31以下の数が4個以上ありますか?」4つあるのでYesです。
- 範囲は25から31の間に絞られました。次は$ X = (25+31)/2 = 28 $です。「28以下の数が4個以上ありますか?」3つしかないのでNoです。
- 範囲は28から31の間に絞られました。次は$ X = (28+31)/2 = 29 $です。「29以下の数が4個以上ありますか?」3つしかないのでNoです。
- 範囲は29から31の間に絞られました。次は$ X = (29+31)/2 = 30 $です。「30以下の数が4個以上ありますか?」4つあるのでYesです。
ここで29はNoであり30はYesであることが確認されたので、その境目は30です。よって答えは30となります。合っていますね。
問題の制約を見てみると積のあり得る最大値は$ 10^9 \times 10^9 = 10^{18} $となります。よって探索範囲は$1$から$10^{18}$までとなり、$ \log_{2} 10^{18} = 59.794705...$なので60回で完全に収束する計算になります。十分な効率です。
「ちょっと待て。二分探索で高速に解けるのは分かったけれども、『X以下の数がK個以上ありますか?』という問いに答えるためには結局全ての積を計算しておく必要が生じ、先と同じ問題が発生するのではないか」
こう思われる方がいるかもしれませんが、実は工夫することで十分高速に「X以下の数がK個以上ありますか?」という問いに答えることができます。
「全ての積の中にX以下の数が幾つあるか」を数えます。
ここで競技プログラミングでよくある考え方をしますが、「全ての積の中にX以下の数が幾つあるかを考える」ことはややこしいので、
数列Aの中から数を一つ選び(これをMとします)、数列Bの要素の中でMとの積がX以下になるものが幾つあるか数えることを考えます。
言葉で説明されてもピンと来ないと思うので具体的に操作を説明します。
- 上例の$ A = {7, 6, 5} $のうち最初の$7$を取り出します。よって$ M = 7 $です。
- 上例の1ステップ目を取って$ X = 50 $とします。数列Bの要素の中で$ M = 7 $との積が50以下になるものは?$ 7 \times 9 = 63, 7 \times 6 = 42, 7 \times 1 = 7 $ということで、二つです。
このような操作をします。
これを数列Aの数字全てに対して行うことで「全ての積の中にX以下の数が幾つあるか」を数えることができます。
「結局数列Aと数列Bのすべての組み合わせを見ているじゃないか」と思うかもしれません。実は全ての組み合わせを見る必要はありません。
数えたいものを数式で表現してみます。
$ M \times B_{1-N} <= X $ 数えるべきはこれです。1からNの各Bの値に対してMを書けた値がX以下であるものの数ですね。
ここで式変形をします。
$ B_{1-N} <= X/M $ 両辺をMで割るとこうなります。こうすると求めたいものは各Bの値の中で、$X/M$より小さい値の数となります。
$ M = 7, X = 50 $の例だと、$ 50/7 = 7$よりも小さい値はBの中に幾つあるか?という話になって、これは6と1の二つです。
だからどういうことか?というと、実は 「数列の中である数よりも小さい数は幾つあるか?」という問題は二分探索で高速に解ける ことで有名です。
単調性を得るために最初に数列をソートしておく必要がありますが、それさえ出来れば長さが$ 10^5 $でも最大17回の計算で求めることができます。
念のためC++でコードを書いておくと、upper_boundという配列に対する二分探索をやってくれる便利な関数もあるので
long long S = X/M;
// itr: X/Mよりも大きい数がどの位置にあるかの情報が入る
auto itr = upper_bound(B.begin(), B.end(), S);
// itrの位置から数列Bの先頭位置(B.begin())を引くとX/M以下の数の個数が求まる。
long long count = itr-B.begin();
このようなコードで上記の処理を行うことができます。
よって、「数列Aの中から数Mを一つ選び、数列Bの要素の中でMとの積がX以下になるものが幾つあるかを数える」という問題は最大でも$\log_{2} 10^5 = 17$回の計算で解けることがわかりました。
つまり数列Aの数を全て試しても$10^5 \times 17$程度の計算量で済みます。
以上のことから 「Xより小さい数(X以下の数)がK個以上ありますか?」という二分探索の問いに対して十分高速に解を出すことが出来ることがわかりました。
となれば後は二分探索ですが、先に書いた通り最大でも60回で計算は終了します。
よって計算量は最大でも$ 10^5 \times 17 \times 60 $程度となって、これは1億回程度となりC++であれば十分間に合います。
pythonでは2秒以内に終わるか少し心もとないですが、「Xより小さい数(X以下の数)がK個以上ありますか?」を判定するパートで二分探索ではなくしゃくとり法というアルゴリズムを用いれば更に高速化され、$ 10^5 \times 60 $程度で解けると思います。
そもそもこの問題の元の制約は$ N \leq 30000 $なので、pythonでも十分に解ける制約になっています。話の見栄えのために私が盛りました(堂々)。あとはPyPyなりCythonなりを使っても通せると思います。
ちなみに長々と説明しましたが、実のところコードはあまり複雑ではありません。以下の通り処理部分だけなら20行程度で書くことができます。
# include <bits/stdc++.h>
const long long LINF = 1e18;
typedef long long ll;
using namespace std;
bool check(ll X, ll n, ll k, const vector<ll> &a, const vector<ll> &b) {
ll cnt = 0;
for (int i = 0; i < n; ++i) {
ll s = X/a[i];
cnt += upper_bound(b.begin(), b.end(), s)-b.begin();
}
return (cnt >= k);
}
int main() {
ll n,k; cin>>n>>k;
vector<ll> a(n), b(n);
for (int i = 0; i < n; ++i) cin>>a[i];
for (int i = 0; i < n; ++i) cin>>b[i];
sort(a.begin(), a.end());
sort(b.begin(), b.end());
// 二分探索
ll ng = 0; ll ok = LINF+10;
while (abs(ok-ng) > 1) {
ll mid = (ok+ng)/2;
// 演算結果がX以下となるものがK個以上あるかどうか?
if (check(mid, n, k, a, b)) ok = mid;
else ng = mid;
}
cout << ok << '\n';
return 0;
}
まとめ
いかがでしたか?
この記事の目的は、主に未経験の人が持つ競技プログラミングへの偏見に対して反論し、また競技プログラミングの面白みを伝えることで未経験の人に興味を持ってもらうことです。
二分探索を暗記していたからといって、上述の問題がそう簡単に解けますか?そもそも全ての積を求めてソートする以外の解法を思いつく人が何人いるでしょうか。慣れていない人では、二分探索が適用できることすら見抜けないでしょう。
競技プログラミングで養われる能力は、アルゴリズムを運用する能力、アルゴリズムが適用できる問題を見抜く能力だと私は考えています。
「アルゴリズムを覚えても実務で使うところがない。役に立たない」という考えもよく耳にします。もちろん、フロントエンドでHTMLとCSSを書くような業務では競技プログラミングの知識など役に立ちません。故に一理ありますが、実際のところ「アルゴリズムが活用できる問題を見抜けていない」という側面もあるように思われます。
そうでなくても、何かしらのロジックを組むような業務では多かれ少なかれ、競技プログラミングで培った経験が活きてくることに違いはないでしょう。
実装は速くなるし、綺麗なロジックを書く練習ができます。確かに競技プログラマの書くコードは汚いですが、それは変数の命名やマクロの作法が実装の高速化を第一としているからに過ぎません。ロジック自体は簡潔で分かりやすく組めるようになります(汚いロジックを無理矢理腕力で通す能力もついてしまうことはあります。まあそれはそれで)。
魔法のように鮮やかな手法で課題を解決し、信じられないような速度で正確にバグのないコードを書く。そのような能力が役に立たないはずはないと私は確信しています。