ABC272 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC272(AtCoder Beginner Contest 272)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

A - Integer Sum　Dif:8

Aをリストで受け取り、合計を出力します。
リストの合計は
sum(リスト)
で計算できます。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
N=int(input())
A=list(map(int,input().split()))

# Aの合計を出力
print(sum(A))

B - Everyone is Friends　Dif:139

各舞踏会について、同時に参加していた人の組を二次元配列(=表)へ記録していきます。
二次元配列の名前をPairとしましょう。
例えばPair[1][2]=1なら人1と人2は同じ舞踏会に参加している、=0なら参加していないということを表します。

二次元配列の初期値は全て0とします。二次元配列は以下のように作ります。
表の名前=[[初期値]*(列数+1) for i in range(行数+1)]

Pair=[[0]*(N+1) for i in range(N+1)]

人数はN人ですが、pythonの場合、0行目、1行目、...と0番目から始まるため行数、列数は(N+1)とすることに注意しましょう。
次にk,xを受け取って組を記録していきます。

for a in range(k):
    for b in range(a+1,k):
        Pair[x[a]][x[b]]=1

上記のように書くことで
a b
0 1
0 2
...
0 k-1
1 2
1 3
...
1 k-1
2 3
2 4
...
k-2 k-1
という順番で代入しながら処理ができます。x[a],x[b]はxのa番目、b番目を表します。
すなわちある舞踏会参加者の0番目と1番目、0番目と2番目、...、(k-2)番目と(k-1)番目が一緒に参加していたと記録できるというわけです。

最後に全組について同時に参加しているか確認します。
すなわち人1と人2、人1と人3、...、人2と人3、人2と人4、...、人(N-1)と人Nが同時に参加しているかPairを確認していきます。

for a in range(1,N+1):
    for b in range(a+1,N+1):
        if Pair[a][b]==0:
            print("No")
            exit()

上記のように書くことで
a b
1 2
1 3
1 4
...
1 N
2 3
2 4
...
N-1 N
という順番で代入しながら処理できます。
一組でも同時に参加していない組がある、すなわちPairが0となっている組があれば「No」を出力して終わりです。
全ての組が参加していれば「Yes」を出力します。

【提出】

# 入力の受け取り
N,M=map(int,input().split())

# 同時に参加している人の組の記録
# (例)Pair[1][2]=1なら人1と人2が同時に参加している
Pair=[[0]*(N+1) for i in range(N+1)]

# M回
for i in range(M):
    # リストで受け取り
    kx=list(map(int,input().split()))
    # 0番目がk
    k=kx[0]
    # 1番目以降がx
    x=kx[1:]

    # a=0~(k-1)
    for a in range(k):
        # b=(a+1)~(k-1)
        for b in range(a+1,k):
            # x[a]とx[b](参加者のa番目とb番目)が同時に参加している
            Pair[x[a]][x[b]]=1

# a=1~N
for a in range(1,N+1):
    # b=(a+1)~N
    for b in range(a+1,N+1):
        # 人aと人bが同時に参加していなければ
        if Pair[a][b]==0:
            # 「No」を出力
            print("No")
            # 終了
            exit()

# 全組同時に参加していればここまで来る
# 「Yes」を出力
print("Yes")

C - Max Even　Dif:167

足して偶数になるのは
偶数+偶数
奇数+奇数
のどちらかです。

Aの要素を偶数と奇数に振り分け、大きい順にソートします。
偶数の中で最も大きいもの+偶数の中で次に大きいもの
奇数の中で最も大きいもの+奇数の中で次に大きいもの
をそれぞれ計算し、最大のものを確認します。

Aにある偶数、奇数が2個未満の場合は足し算できないことに注意してください。

【提出】

# 入力の受け取り
N=int(input())
A=list(map(int,input().split()))

# 偶数のリスト
ev=[]
# 奇数のリスト
od=[]

# i=0~(N-1)
for i in range(N):
    # A[i]が偶数⇔2で割った余りが0
    if A[i]%2==0:
        # 偶数リストに追加
        ev.append(A[i])
    # そうでなければ(A[i]が奇数)
    else:
        # 奇数リストに追加
        od.append(A[i])

# 大きい順にソート
ev.sort(reverse=True)
od.sort(reverse=True)

# 答え(初期値は-1)
ans=-1

# 偶数リストの長さが2以上ならば
if 2<=len(ev):
    # ansと「偶数の中で最も大きいもの+偶数の中で次に大きいもの」の大きい方
    ans=max(ans,ev[0]+ev[1])
# 奇数リストの長さが2以上ならば
if 2<=len(od):
    # ansと「奇数の中で最も大きいもの+奇数の中で次に大きいもの」の大きい方
    ans=max(ans,od[0]+od[1])

# 答えの出力
print(ans)

D - Root M Leaper　Dif:804

まず距離がちょうど√Mというのを行方向、列方向の移動量で考えます。
例えばM=5の場合、√(1^2+2^2)=√5であることから
行方向に+1,列方向に+2→(+1,+2)
行方向に+1,列方向に-2→(+1,-2)
行方向に-1,列方向に+2→(-1,+2)
行方向に-1,列方向に-2→(-1,-2)
行方向に+2,列方向に+1→(+2,+1)
行方向に+2,列方向に-1→(+2,-1)
行方向に-2,列方向に+1→(-2,+1)
行方向に-2,列方向に-1→(-2,-1)
この8方向に動けばいいということがわかります。

M≤10^6ですからa=-10^3~10^3,b=-10^3~10^3としてa^2+b^2=Mとなるようなa,bを全探索で探せばいいです。(実装では保険を掛けて-10^3より少し小さい数、10^3より少し大きい数まで探索しています)
※√(a^2+b^2)=√Mとすると少数が発生し、誤差がでる可能性があります。必ず整数のみの計算で確認しましょう。
ちなみにNの大きさを考慮すると探索範囲をもうちょっと小さくできたりもしますが、このやり方でもTLEしないのでそこまで考える必要もないです。

方向がわかったら次に(1,1)からの移動回数を数えていきます。
例として
N M：10 5
としましょう。方向は先程見た通り行方向、列方向に+1,-1,+2,-2進む形です。
イメージ的には以下のように進めたいです。
まず(1,1)に「0」と書きます。

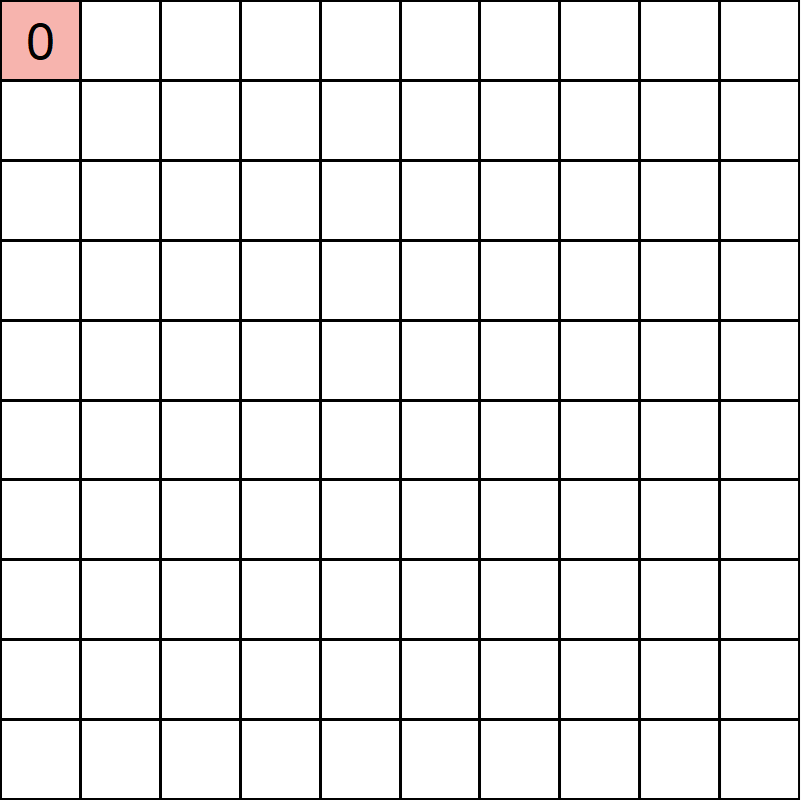
「0」を書いた(1,1)から進める場所に0+1=「1」を書きます。

「1」を書いたマスから進める場所に場所に1+1＝「2」を書きます。
ただしすでに数字が書かれているマスは無視します((3,2)から(1,1)へ進めますが(1,1)にはすでに「0」が書いています)

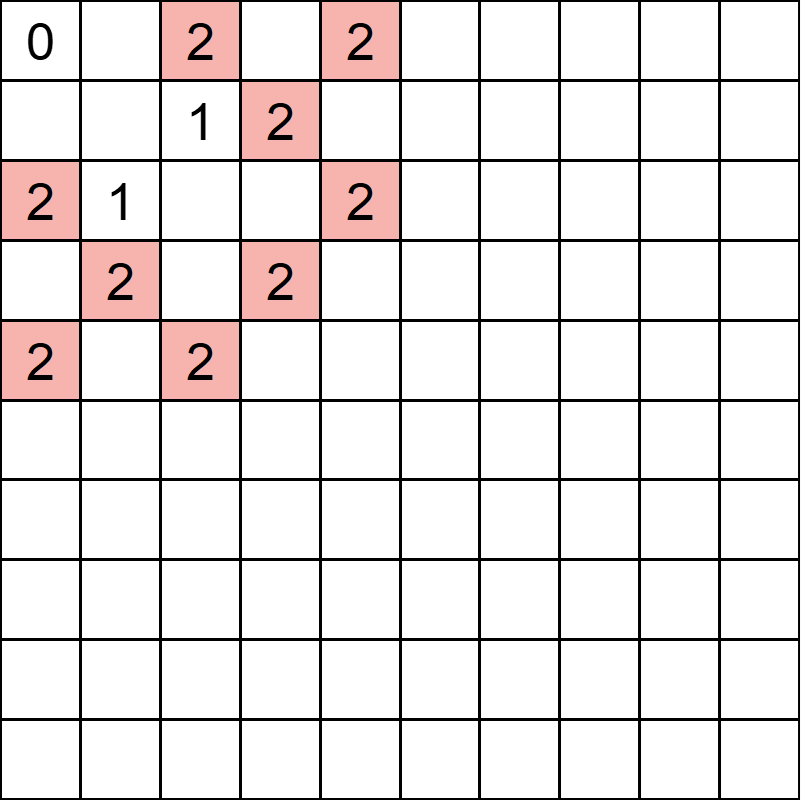
これを繰り返すことで到達できる全てのマスに数字を書くことができます。

各マスから進めるマスの確認のためBFSを使います。
BFSは幅優先探索(breadth first search)の略称で、グラフを探索するアルゴリズムです。

BFSの解説動画を作りましたので、本問が難しいと感じた方は是非御覧ください。

(1)スタート地点(1,1)に「0」を書き込む
(2)キューにスタート地点(1,1)を追加
(3)キューから座標を取り出し(今いる行、今いる列)、書かれている数字を確認
(4)今いるマスから進めるマスについてまだ数字が書き込まれていなければ「今いるマスの数字+1」を書き込み、キューへ追加する
(5)キューが空でなければ(3)へ戻る

最後にマス目の数字を出力すれば終わりです。

pythonでは間に合わないのでpypyで提出します。

【提出】

# pypyで提出

# 入力の受け取り
N,M=map(int,input().split())

# 方向の記録
d=[]

# a=-10^3(より少し小さめ)~10^3(より少し大きめ)
for a in range(-10**3-10,10**3+10):
    # b=-10^3(より少し小さめ)~10^3(より少し大きめ)
    for b in range(-10**3-10,10**3+10):
        # a^2+b^2=Mならば
        if a**2+b**2==M:
            # (a,b)方向へ進める
            d.append([a,b])

# マス目(初期値は「-1」)
Grid=[[-1]*(N+1) for i in range(N+1)]

# (1)スタート地点(1,1)に「0」を書き込む
Grid[1][1]=0

# dequeのインポート
from collections import deque
# キューを用意
que=deque()
# (2)キューにスタート地点(1,1)を追加
que.append([1,1])

# (5)キューが空でなければ(3)へ戻る
while 0<len(que):
    # (3)キューから座標を取り出し(今いる行、今いる列)、書かれている数字を確認
    # キューから座標を取り出し
    NowG,NowR=que.popleft()
    # 今いるマスの数字
    Num=Grid[NowG][NowR]

    # (4)今いるマスから進めるマスについてまだ数字が書き込まれていなければ「今いるマスの数字+1」を書き込み、キューへ追加する
    # dから行方向、列方向の増加量を取り出し
    # Gd,Rd：dの各要素を順に格納
    for Gd,Rd in d:
        # 1≤NowG+Gd≤N(今いるマスから行方向にGd進んだマスがマス目の範囲内)
        # かつ
        # 1≤NowR+Rd≤N(今いるマスから列方向にRd進んだマスがマス目の範囲内)
        if 1<=NowG+Gd<=N and 1<=NowR+Rd<=N:
            # まだ数字が書き込まれていなければ(-1ならば)
            if Grid[NowG+Gd][NowR+Rd]==-1:
                # 「今いるマスの数字+1」を書き込む
                Grid[NowG+Gd][NowR+Rd]=Num+1
                # キューに追加
                que.append([NowG+Gd,NowR+Rd])

# G=1~N
for G in range(1,N+1):
    # G行目の1列目以降を出力(「*」をつけるとカッコなしで出力できる)
    print(*Grid[G][1:])

【広告】

『AtCoder 最速で緑になる 基礎・典型50問詳細解説』

ABC201～250から基礎・典型問題50問をとてつもなく丁寧かつ詳細に解説した本(kindle)、pdf(booth)です。
灰色、茶色コーダーにおすすめ！
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BBB7RKTP

【booth(pdf)】
https://booth.pm/ja/items/4102300

冒頭5問をサンプルとして無料公開しています
https://qiita.com/sano192/items/6361ed72106cb6dd5843

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312