Go to Qiita Advent Calendar 2024 Top
LoginSignup
4
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@sano192

ABC250 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

Last updated at Posted at 2022-05-09

ABC250(AtCoder Beginner Contest 250)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

その他のABC解説、動画などは以下です。

A - Adjacent Squares

辺でつながっているというのは要するに(R,C)の上下左右のマスの意味です。
それぞれのマスの座標は以下のようになります。
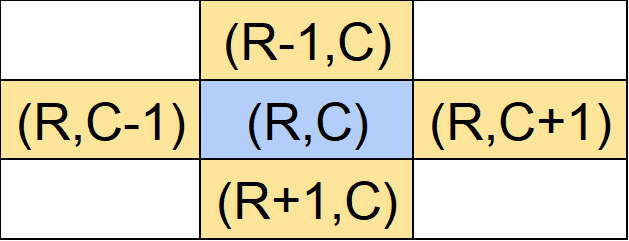
ABC250_A_1.png

それぞれのマスがマス目の中にあるか確認します。
例えばH=10,W=10で(R,C)=(1,5)の場合、
右：(R,C+1)=(1,6)=マスの中
上：(R-1,C)=(0,5)=マスの外
となります。

4つのマスがマス目の中にある条件は以下のようになります。
上(R-1,C)：1≤R-1
下(R+1,C)：R+1≤H
右(R,C+1)：C+1≤W
左(R,C-1)：1≤C-1

条件を満たしたら答えの個数を一個増やすというかたちでカウントしていきます。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
H,W=map(int,input().split())
R,C=map(int,input().split())

# 答えの個数
ans=0

# 上マスがマス目の中にあるか
if 1<=R-1:
    # 答えにプラス1
    ans+=1
# 下マスがマス目の中にあるか
if R+1<=H:
    ans+=1
# 左マスがマス目の中にあるか
if 1<=C-1:
    ans+=1
# 右マスがマス目の中にあるか
if C+1<=W:
    ans+=1

# 答えの出力
print(ans)

B - Enlarged Checker Board

例として以下の入力を考えます。
N：4
A：3
B：3
ABC250_B_1.png
外側のN×Nの部分と、内側のA×Bの部分は分けて考えましょう。

・N=1,3,5,...と奇数の場合
　各行は白B個、黒B個、白B個、黒B個、...(N列)となります。
　これらがA行続きます。
・N=2,4,6,...と奇数の場合
　各行は黒B個、白B個、黒B個、白B個、...(N列)となります。
　これらがA行続きます。

これらをそのままfor文で書ければOKです。

【提出】

# 入力の受け取り
N,A,B=map(int,input().split())

# 外側の行
# NGyou=1~N
for NGyou in range(1,N+1):
    # 奇数の場合
    # ⇔2で割った余りが1
    if NGyou%2==1:
        # a=1~A
        for a in range(1,A+1):
            # 行の中身
            Gyou=""
            # 外側の列
            # NRretu=1~N
            for NRetu in range(1,N+1):
                # 奇数の場合
                # ⇔2で割った余りが1
                if NRetu%2==1:
                    # 白マスがB個
                    Gyou+="."*B
                # 偶数の場合
                else:
                    # 黒マスがB個
                    Gyou+="#"*B
            # 出力
            print(Gyou)

    # 偶数の場合
    else:
        # a=1~A
        for a in range(1,A+1):
            # 行の中身
            Gyou=""
            # 外側の列
            # NRretu=1~N
            for NRetu in range(1,N+1):
                # 奇数の場合
                # ⇔2で割った余りが1
                if NRetu%2==1:
                    # 黒マスがB個
                    Gyou+="#"*B
                # 偶数の場合
                else:
                    # 白マスがB個
                    Gyou+="."*B
            # 出力
            print(Gyou)

C - Adjacent Swaps

xが来るたびにxが書かれたボールがどこにあるか確認しているとTLEします。
あらかじめ全ての番号について書かれたボールがどこにあるか記録しておきましょう。

N=7の場合を考えます。
それぞれのボールの場所を数列Aで表します。すなわち最初は
A：1 2 3 4 5 6 7
となっています。
このとき同時にそれぞれのボールの場=インデックス番号も記録しておきます。
ABC250_C_1.png

x=3が来た場合
3と4を入れ替えます。Aは以下のようになります。
A：1 2 4 3 5 6 7
同時に記録しているインデックス番号も変更します。
3は4番目、4は3番目になりました。
ABC250_C_2.png

こうしてインデックス番号を記録しておくと次にまたx=3が来た場合、
インデックス番号の表から3が4番目にあり、5番目の5と入れ替えればよいということがすぐに(O(1)で)わかります。

実装ではxが右端の場合、すなわちxのインデックス番号=Nの場合とそうでない場合に分けることに注意してください。

Aを出力するときはAの1番目からを出力するのでprint(A[1:])となります。さらに「*」をつけることで[]なしで出力できます。

【提出】

# 入力の受け取り
N,Q=map(int,input().split())

# A=[0,1,2,...,N]
A=list(range(N+1))
# indx=[0,1,2,...,N]
indx=list(range(N+1))

# Q回
for i in range(Q):
    # 入力の受け取り
    x=int(input())

    # xのインデックス番号を確認
    x_indx=indx[x]

    # xのインデックス番号=Nの場合
    if x_indx==N:
        # xの左のボールに書いている番号
        left_x=A[x_indx-1]
        # 入れ替える
        A[x_indx],A[x_indx-1]=A[x_indx-1],A[x_indx]
        # インデックス番号を更新する
        indx[x]=x_indx-1
        indx[left_x]=x_indx

    # xのインデックス番号≠Nの場合
    else:
        # xの右のボールに書いている番号
        right_x=A[x_indx+1]
        # 入れ替える
        A[x_indx],A[x_indx+1]=A[x_indx+1],A[x_indx]
        # インデックス番号を更新する
        indx[x]=x_indx+1
        indx[right_x]=x_indx 

# Aを出力
# 0番目は不要なので1番目~
# 「*」をつけると[]なしで出力できる
print(*A[1:])

D - 250-like Number

変数がいくつか出てくる問題はまず変数のどれかを固定して考えるのがセオリーです。
本文の場合、pを固定すればpq^3≤Nとなる最大の素数qを見つけることができます。
例えばN=1000、p=2であれば2*7^3=686≤1000ですから、q=3,5,7の3つが使えるということがわかります。
※(p,q)=(2,3),(2,5),(2,7)の組が可能ということ
より一般にはpをi番目の素数、pq^3≤Nとなる最大の素数qがk番目の素数だったとして(k-i)個のqが使えます。

素数のリストはエラトステネスの篩を使って用意します。(詳しくは後述の「エラトステネスの篩」を読んで下さい)
用意するのは最大10^6までの素数で良いです。N≤10^18であるため、pが10^6を超えるとp<qよりN<p*q^3となってしまうためです。

各p(=1番目の素数,2番目の素数,...)についてpq^3≤Nとなる最大の素数qは何番目にあるか確認していきます。これは尺取法を使います。
例えばp=5番目の素数だったとき、pq^3≤Nとなる最大の素数qが15番目だったとします。
次にp=6番目の素数を考えますが、このときpq^3≤Nとなる最大の素数qは必ず15番目以下の素数となります。
(5番目の素数<6番目の素数であるからqは15番目の素数以下でなければなりません)
よって16番目以上の素数はqの候補となりません。q=15番目の素数,14番目の素数,...と減らしながらpq^3≤Nとなっているか確認していきます。
このようにpは1つずつ増え、対応するqは1つずつ減らしていくという動きが尺取り虫の動き方に似ているので尺取法といいます。

エラトステネスの篩
エラトステネスの篩は指定した数以下の素数を求めるアルゴリズムの一つです。
手順は以下です。
(1)0~Nまで全てTrueのリストIsPrimeを作る。(最終的にIsPrime=Trueのものが素数)
(2)i=2,3,...,√Nのiについて
　・iが素数でない⇔IsPrime[i]=Falseなら次のiへ
　・iが素数⇔IsPrime[i]=Trueなら
　　i*2,i*3,i*4,...についてIsPrimeをFalseにする(iの倍数は素数ではない)
(3)IsPrimeがTrueになっている数のリストを返す
計算量はちょっとややこしく、O(NloglogN)となります。詳しくは以下のサイトがわかりやすいです。

【提出】

# エラトステネスの篩
def Eratosthenes(N):
    # 素数であるかの判定リスト
    IsPrime=[True]*(N+1)

    # i=2,3,4,...
    i=2
    # i≤√Nまで⇔i^2≤Nまで
    while i**2<=N:
        # iが素数でなければ
        if IsPrime[i]==False:
            # 次のiへ
            i+=1
            continue
        
        # k=2,3,4,...
        k=2
        while i*k<=N:
            # iの倍数は素数でない
            IsPrime[i*k]=False
            # 次のkへ
            k+=1

        # 次のkへ
        i+=1

    # 素数リスト
    PList=[]

    # i=2~N
    for i in range(2,N+1):
        # iが素数ならば
        if IsPrime[i]==True:
            # リストへ入れる
            PList.append(i)

    # リストを返す
    return PList

# 入力の受け取り
N=int(input())
# 10^6以下の素数リストを作成
P=Eratosthenes(10**6)

# 答え
ans=0

# 素数リストの長さ
len_P=len(P)

# 最後の素数の番号
k=len_P-1

# i=0~(len_P-1)
for i in range(len_P):

    # p=i番目の素数
    # q=k番目の素数
    # p*q^3≤Nとなるまでkを減らしていく
    while 0<k and N<P[i]*P[k]**3:
        k-=1

    # k≤iとなったら
    if k<=i:
        # 終了
        break

    # i+1,i+2,...,k番目の素数までqとして使用できる
    # ⇔(k-i)個
    ans+=k-i

# 答えの出力
print(ans)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312

4
4
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
4

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?