More than 1 year has passed since last update.

ABC262 A～C問題ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

Last updated at 2022-08-20Posted at 2022-08-05

ABC262(AtCoder Beginner Contest 262)　A～C問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

A - World Cup　Dif:8

スポーツ大会は4年に1回必ず開催されます。
よって
・Yを4で割った余りが2→西暦Y年に開催
・(Y+1)を4で割った余りが2→西暦(Y+1)年に開催
・(Y+2)を4で割った余りが2→西暦(Y+2)年に開催
・(Y+3)を4で割った余りが2→西暦(Y+3)年に開催
と判定しましょう。

Yを4で割った余りはY%4で計算できます。
判定にはifを使います。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
Y=int(input())

# Yを4で割った余りが2なら
if Y%4==2:
    # Yを出力
    print(Y)
# (Y+1)を4で割った余りが2なら
elif (Y+1)%4==2:
    # (Y+1)を出力
    print(Y+1)
# (Y+2)を4で割った余りが2なら
elif (Y+2)%4==2:
    # (Y+2)を出力
    print(Y+2)
# (Y+3)を4で割った余りが2なら
elif (Y+3)%4==2:
    # (Y+3)を出力
    print(Y+3)

B - Triangle (Easier)　Dif:220

単純無向グラフは多重辺がなく、ループもなく、向きのないグラフです。
※ここでいうループは頂点①から頂点①を結ぶというような辺が存在することを言います
要するに以下のような感じです。(入力例1)

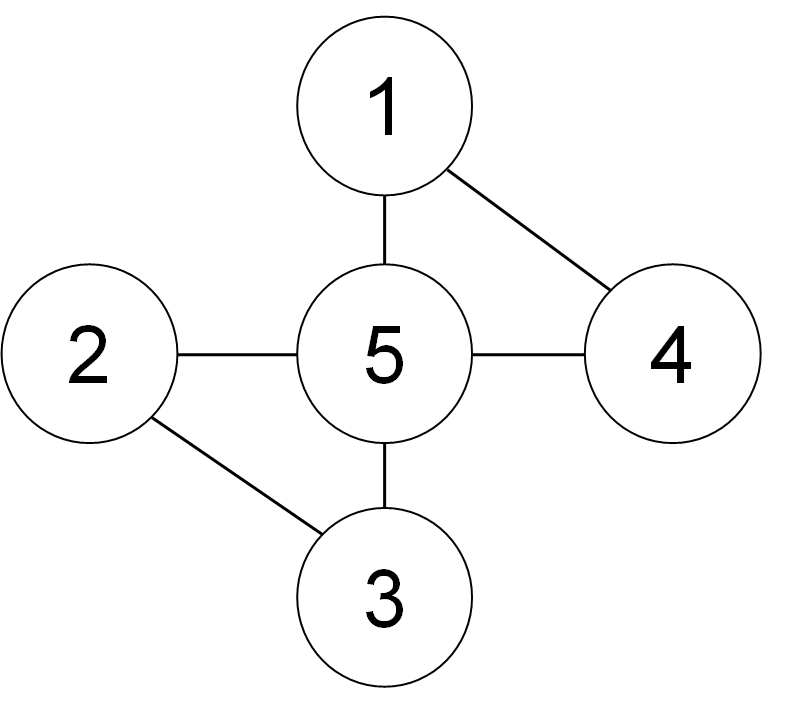
頂点の数は100個以下なので全ての組み合わせを考えても100C3=161700通りしかありません。これなら全組み合わせを確認しても実行制限時間に十分間に合います。

まずどの頂点がつながっているかを記録しましょう。これは二次元配列で、つながっている頂点をTrueとして記録します。
二次元配列connectを用意します。最初は全て初期値Falseとします。
入力U,Vを受け取ってconnect[U][V]とconnect[V][U]をTrueにします。これで記録が完了です。

# つながっている頂点を記録する二次元配列
# 最初は全ての初期値をFalseにする
connect=[[False]*(N+1) for i in range(N+1)]

# M回
for i in range(M):
    # 入力の受け取り
    U,V=map(int,input().split())
    # 頂点Uと頂点Vがつながっている⇔Trueと記録
    connect[U][V]=True
    connect[V][U]=True

次に(a,b,c)を全組作ります。
以下のように書くと全ての組を作れます。

# a=1~N
for a in range(1,N+1):
    # b=(a+1)~N
    for b in range(a+1,N+1):
        # c=(b+1)~N
        for c in range(b+1,N+1):

これで
(a,b,c)
(1,2,3)
(1,2,4)
(1,2,5)
...
(1,3,4)
(1,3,5)
...

(2,3,4)
(2,3,5)
...
(N-2,N-1,N)
といい感じに組が作れます。
あとはa,b,c全てがつながっているかを確認し、つながっているなら答えにカウントしていけばOKです。

【提出】

# 入力の受け取り
N,M=map(int,input().split())

# つながっている頂点を記録する二次元配列
# 最初は全ての初期値をFalseにする
connect=[[False]*(N+1) for i in range(N+1)]

# M回
for i in range(M):
    # 入力の受け取り
    U,V=map(int,input().split())
    # 頂点Uと頂点Vがつながっている⇔Trueと記録
    connect[U][V]=True
    connect[V][U]=True

# 答え
ans=0

# a=1~N
for a in range(1,N+1):
    # b=(a+1)~N
    for b in range(a+1,N+1):
        # c=(b+1)~N
        for c in range(b+1,N+1):
            # a,b,cが全てつながっていれば
            if connect[a][b]==True and connect[b][c]==True and connect[c][a]==True:
                # 答えにプラス1
                ans+=1

# 答えの出力
print(ans)

C - Min Max Pair　Dif:362

入力例1を眺めているとどうやら
(1)ai=i,aj=j
(2)ai=j,aj=i
となっている(i,j)の組ならばよさそうだということがわかります。
別々に数えてみましょう。

(1)ai=i,aj=j
x=1,2,3,...についてax=xとなっているようなものがいくつあるかを数えます。
例えば6個あるならそれらから2個取り出す組み合わせの数ですから
6C2=15
と計算できるわけです。k個あるならkC2=(k(k-1)/2)個です。

(2)ai=j,aj=i
i=1,2,3,...についてai=jとしたとき、aj=iとなっているか確認してけばOKです。
i<jという条件に注意してください。

(1),(2)それぞれを確認して足せば終わりです。

入力を受け取る時、aをリストでそのまま受け取るとa[0]=a1,a[1]=a2,...と一個ずれてめんどうなので、a[0]=0などを埋めておくと良いでしょう。

【提出】

# 入力の受け取り
N=int(input())
# a[0]を適当な数(=0)で埋めておく
a=[0]+list(map(int,input().split()))

# 答え
ans=0

# (1)ai=i,aj=j
# ax=xとなっているものの個数
k=0

# i=1~N
for i in range(1,N+1):
    # a[i]=iならば
    if a[i]==i:
        # kにカウント
        k+=1

# kC2=(k*(k-1)//2)個
ans+=k*(k-1)//2

# (2)ai=j,aj=i
# i=1~N
for i in range(1,N+1):
    # a[i]=j
    j=a[i]
    # i<j　かつ　a[j]=iならば
    if i<j and  a[j]==i:
        # 答えにカウント
        ans+=1

# 答えの出力
print(ans)

【広告】

『AtCoder 最速で緑になる基礎・典型50問詳細解説』

ABC201～250から基礎・典型問題50問をとてつもなく丁寧かつ詳細に解説した本(kindle)、pdf(booth)です。
灰色、茶色コーダーにおすすめ！
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BBB7RKTP

【booth(pdf)】
https://booth.pm/ja/items/4102300

冒頭5問をサンプルとして無料公開しています
https://qiita.com/sano192/items/6361ed72106cb6dd5843

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737