ABC259 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC259(AtCoder Beginner Contest 259)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

A - Growth Record　Dif:34

X≤Mならば身長の伸びが止まっているので答えはTcmです。
M<Xならば(X-M)年Dcmずつ身長が伸びた結果Tになったわけなので答えは(T-(X-M)D)cmです。

これらをifで条件分岐します。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
N,M,X,T,D=map(int,input().split())

# X≤Mならば
if X<=M:
    # Tcm
    print(T)
# そうでなければ(M<X)
else:
    # (T-(X-M)D)cm
    print(T-(X-M)*D)

B - Counterclockwise Rotation　Dif:180

回転行列を知っていれば
回転後のx座標=acos(d)-bsin(d)
回転後のy座標=asin(d)+bcos(d)
とわかります。

回転行列を知らなくても「座標　回転」で検索すればすぐに出てきます。コンテスト中でも知らないことはググりましょう。

sin,cosはmathライブラリで計算できます。
import mathと書いた後、math.sin,math.cosと書くことでそれぞれの計算ができます。
が、これらは度数法ではなく弧度法で値を指定するので、入力の度数法を弧度法に変換する必要があります。
math.radians(度数)と書くことでラジアンへ変換できます。

入力例1のサンプルを試すと
-2.0000000000000004 -1.9999999999999998
と違う値が出てきて焦った人がいるかも知れません。が、これは単に計算の誤差であり、「各出力について、解との絶対誤差または相対誤差が10^−6以下であれば正解として扱われる。」と記述があるので問題ありません。

【提出】

# 入力の受け取り
a,b,d=map(int,input().split())

# mathライブラリのインポート
import math

# 度数法→弧度法へ変換
d=math.radians(d)

# 回転後の座標を計算
x=a*math.cos(d)-b*math.sin(d)
y=a*math.sin(d)+b*math.cos(d)

# 答えの出力
print(x,y)

C - XX to XXX　Dif:451

まず各文字がいくつ続いているのかを二次元配列に記録します。
(例)S：abbbaaac
→[['a', 1], ['b', 3], ['a', 3], ['c', 1]]
このような記録方法をランレングス圧縮と呼びます。

ある文字が2つ以上続いているなら文字数を増やすことが可能です。例えば2つ目の['b', 3]を['b', 6]に変えることはできます。
1文字しかない場合は増やすことができず、また減らすこともできません。

「No」となるのは以下の4パターンです。
・文字の種類数が違う
・文字の種類が違う
・S側よりT側の文字が多く、かつSが1文字
・T側よりS側の文字が多い

これらを順に判定すればOKです。

【提出】

# 入力の受け取り
S=input()
T=input()

# 何文字連続しているか記録するリスト
Slist=[]
# 今連続している文字
Now=S[0]
# 連続している文字数
Count=1
 
# i=1~(N-1)
for i in range(1,len(S)):
    # Sのi文字目＝Nowなら
    if S[i]==Now:
        # カウントを増やす
        Count+=1
    # そうでなければ
    else:
        # リストへ記録
        Slist.append([Now,Count])
        # 次の文字へ
        Now=S[i]
        Count=1
# 最後のカウントを追加
Slist.append([Now,Count])

# Tも同じことをする
Tlist=[]
Now=T[0]
Count=1
 
for i in range(1,len(T)):
    if T[i]==Now:
        Count+=1
    else:
        Tlist.append([Now,Count])
        Now=T[i]
        Count=1
Tlist.append([Now,Count])

# ・文字の種類数が違う
if len(Slist)!=len(Tlist):
    # 「No」を出力
    print("No")
    # 終了
    exit()

# i=0~(Slistの長さ-1)
for i in range(len(Slist)):
    # S側の文字
    SMozi=Slist[i][0]
    # T側の文字
    TMozi=Tlist[i][0]

    # S側の文字数
    SCount=Slist[i][1]
    # T側の文字数
    TCount=Tlist[i][1]

    # ・文字の種類が違う
    if SMozi!=TMozi:
        print("No")
        exit()

    # ・S側よりT側の文字が多く、かつSが1文字
    elif SCount<TCount and SCount==1:
        print("No")
        exit() 
    
    # ・T側よりS側の文字が多い
    elif TCount<SCount:
        print("No")
        exit() 
    
# 「Yes」を出力
print("Yes")

D - Circumferences　Dif:947

2つの円が共通の点を持っている、すなわちある円の円周上を進んで別の円周上に移れることを「乗り換え可能」と表現しましょう。
円が「乗り換え可能」かどうかは中心間距離と半径の合計によって決まります。
以下ページの「中心間の距離と半径」というところがわかりやすいです。

コードにするときは誤差が出ないように2乗して計算します。
例えば外接する場合は
d=r1+r2
ですが
d^2=(r1+r2)^2
とします。

スタートの点からゴールの点にいけるかというのは要するにスタートの点が載っている円から「乗り換え可能」な円をいくつか乗り継いでゴールの点が載っている円に到達できるかということです。
「乗り換え可能」な円をグラフに表した時、連結である円同士は到達可能です。

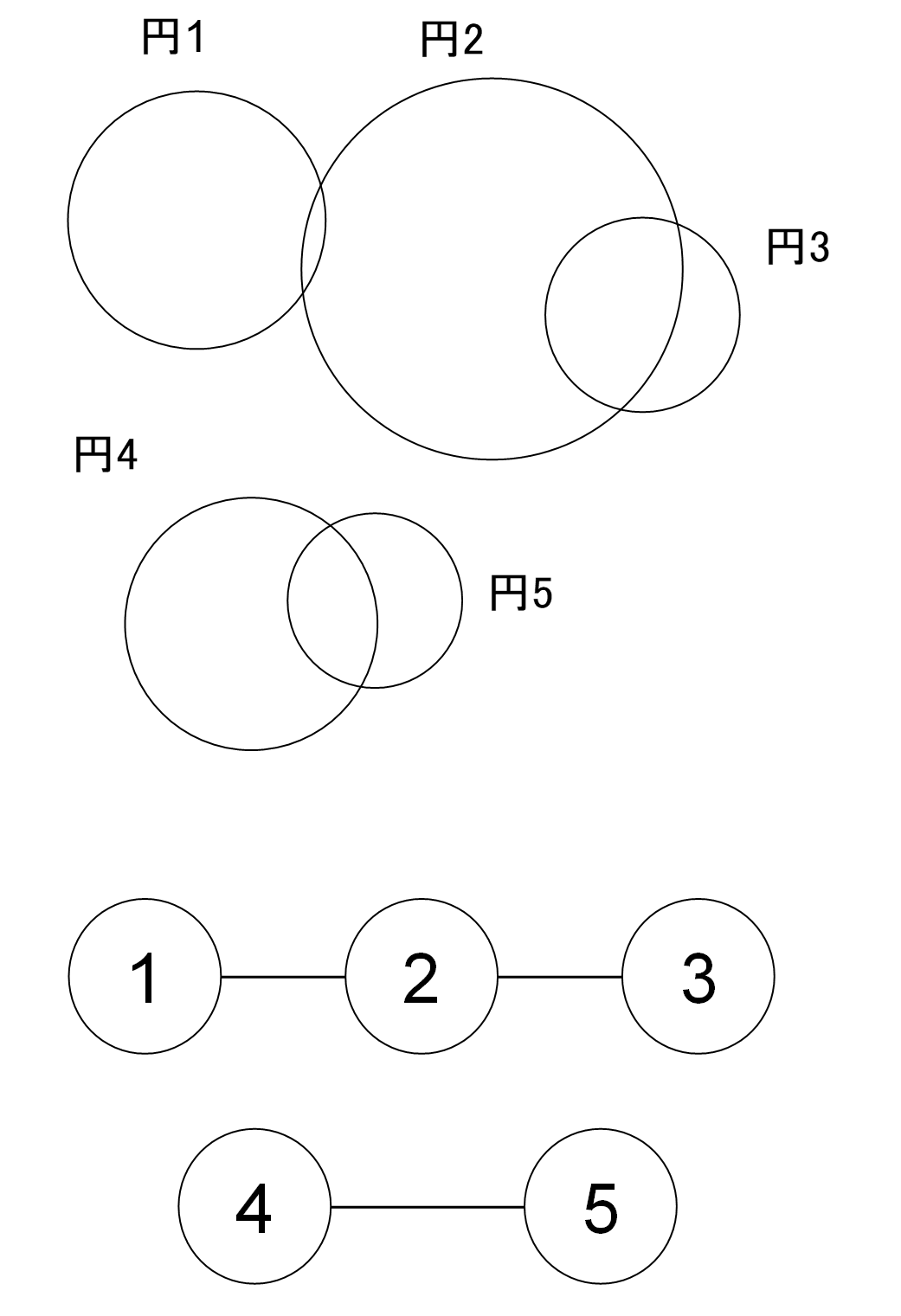
図の例でいうと円1,2,3、円4,5はそれぞれ連結です。

どの円が連結しているかはUnionFindで管理します。

UnionFindはグループ分けを高速でできるデータ構造です。
具体的には以下のことができます。
・a,bを同じグループとする⇔a,bを連結する：【O(logN)くらい】(厳密には違いますがO(logN)くらいと思っておけばOKです)
・a,bが同じグループか判定する⇔a,bが連結か確認する：【O(1)くらい】(厳密には違いますがO(1)くらいと思っておけばOKです)
とにかくめちゃくちゃ速く上記2つができるデータ構造だと覚えましょう。

きちんとした説明はAtCoder公式が解説スライドを作っているのでそちらを御覧ください。

UnionFindの実装はかなり難しいです。ですが問題を解くのにそこまで理解する必要はなく、以下のUnionFindクラスをコピペして使えればOKです。

# UnionFind
class UnionFind:
    def __init__(self,n):
        self.n=n
        self.parent_size=[-1]*n
 
    def leader(self,a):
        if self.parent_size[a]<0: return a
        self.parent_size[a]=self.leader(self.parent_size[a])
        return self.parent_size[a]
 
    def merge(self,a,b):
        x,y=self.leader(a),self.leader(b)
        if x == y: return 
        if abs(self.parent_size[x])<abs(self.parent_size[y]):x,y=y,x
        self.parent_size[x] += self.parent_size[y]
        self.parent_size[y]=x
        return 
 
    def same(self,a,b):
        return self.leader(a) == self.leader(b)
 
    def size(self,a):
        return abs(self.parent_size[self.leader(a)])
 
    def groups(self):
        result=[[] for _ in range(self.n)]
        for i in range(self.n):
            result[self.leader(i)].append(i)
        return [r for r in result if r != []]

上記をコードの最初にコピペしてから以下のように使います。
・初期化：変数名=UnionFind(要素の数)
・グループリーダー(根)の確認：変数名.leader(要素番号)
・グループ化：変数名.merge(要素番号1,要素番号2)
・同一グループかの確認：変数名.same(要素番号1,要素番号2)
　(同一ならTrue,違うグループならFalseを返す)
・所属するグループのサイズ確認：変数名.size(要素番号)
・グループ全体の確認：変数名.groups()

【使用例】

# 初期化：変数名=UnionFind(要素の数)
UF=UnionFind(10)

# グループ化：変数名.merge(要素番号1,要素番号2)
UF.merge(0,2)
UF.merge(1,3)
UF.merge(3,0)

# グループリーダー(根)の確認：変数名.leader(要素番号)
leader_x=UF.leader(1)

# 同一グループかの確認：変数名.same(要素番号1,要素番号2)
if UF.same(1,5)==True:
    print("同一グループ")
else:
    print("別グループ")

# 所属するグループのサイズ確認：変数名.size(要素番号)
size_x=UF.size(1)

# グループ全体の確認：変数名.groups()
print(UF.groups())

連結とは頂点同士をいくつかの辺を使って行き来できる、すなわち頂点同士がつながっているということです。
A,Bをグループ化、というのが頂点の連結、すなわちA,Bに辺を張るということを意味します。

これで「乗り換え可能」可能な円を連結しながら管理します。

あとはスタートの点が載っている円と、ゴールの点が載っている円の組全てについて、連結かどうかを確認します。
連結であれば「Yes」を出力します。

pythonでは間に合わないのでpypyで提出します。

【提出】

# pypyで提出

# UnionFind
class UnionFind:
    def __init__(self,n):
        self.n=n
        self.parent_size=[-1]*n
 
    def leader(self,a):
        if self.parent_size[a]<0: return a
        self.parent_size[a]=self.leader(self.parent_size[a])
        return self.parent_size[a]
 
    def merge(self,a,b):
        x,y=self.leader(a),self.leader(b)
        if x == y: return 
        if abs(self.parent_size[x])<abs(self.parent_size[y]):x,y=y,x
        self.parent_size[x] += self.parent_size[y]
        self.parent_size[y]=x
        return 
 
    def same(self,a,b):
        return self.leader(a) == self.leader(b)
 
    def size(self,a):
        return abs(self.parent_size[self.leader(a)])
 
    def groups(self):
        result=[[] for _ in range(self.n)]
        for i in range(self.n):
            result[self.leader(i)].append(i)
        return [r for r in result if r != []]

# 入力の受け取り
N=int(input())
sx,sy,tx,ty=map(int,input().split())

# 円の情報
p=[]

# N回
for i in range(N):
    # 入力の受け取り
    x,y,r=map(int,input().split())
    # 記録
    p.append([x,y,r])

# UnionFindを用意
UF=UnionFind(N)

# i=0~(N-1)
for i in range(N):
    # k=(i+1)~(N-1)
    for k in range(i+1,N):
        # 座標と半径を取り出し
        ix,iy,ir=p[i]
        kx,ky,kr=p[k]

        # 中心間距離の二乗
        d=(ix-kx)**2+(iy-ky)**2

        # 外接
        if d==(ir+kr)**2:
            # 円iと円kは「乗り換え可能」
            # ⇔連結
            UF.merge(i, k)
        # 2点で交わる
        elif (ir-kr)**2<d<(ir+kr)**2:
            UF.merge(i, k)
        # 内接
        elif d==(ir-kr)**2:
            UF.merge(i, k)

# スタートの点が載っている円
Start=[]
# ゴールの点が載っている円
Goal=[]

# i=0~(N-1)
for i in range(N):
    # 中心、半径の取り出し
    ix,iy,ir=p[i]

    # スタートの点が円周上にあれば
    if (sx-ix)**2+(sy-iy)**2==ir**2:
        # 記録
        Start.append(i)
    # ゴールの点が円周上にあれば
    if (tx-ix)**2+(ty-iy)**2==ir**2:
        # 記録
        Goal.append(i)
# x：スタートの点が載っている円
for x in Start:
    # y：ゴールの点が載っている円
    for y in Goal:
        # 連結なら
        if UF.same(x,y):
            # 「Yes」を出力
            print("Yes")
            # 終了
            exit()

# 「No」を出力
print("No")

【広告】

『AtCoder 最速で緑になる 基礎・典型50問詳細解説』

ABC201～250から基礎・典型問題50問をとてつもなく丁寧かつ詳細に解説した本(kindle)、pdf(booth)です。
灰色、茶色コーダーにおすすめ！
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BBB7RKTP

【booth(pdf)】
https://booth.pm/ja/items/4102300

冒頭5問をサンプルとして無料公開しています
https://qiita.com/sano192/items/6361ed72106cb6dd5843

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312