NOMURA プログラミングコンテスト2022(AtCoder Beginner Contest 253) A~E問題の解説記事です。
灰色~茶色コーダーの方向けに解説しています。
その他のABC解説、動画などは以下です。
更新時はツイッターにて通知します。
https://twitter.com/AtCoder4
野村ホールディングス株式会社様について
本コンテストは野村ホールディングス株式会社様が主催されています。
興味のある方は以下のページを御覧ください。
A - Median? Dif:17
中央値は真ん中の値ですから、大きさがa,b,cかc,b,aの順番になっていればbが中央値になります。
よってa≤b≤cかc≤b≤aになっていれば「Yes」です。この条件をifで確認します。
「Yes」「No」は文字列なので出力の際、"Yes","No"とダブルクオーテーションをつけることに注意してください。
入力の受け取り、出力がわからない方は以下の記事を参考にしてください。
【提出】
# 入力の受け取り
a,b,c=map(int,input().split())
# a,b,cまたはc,b,aの順になっていれば
if a<=b<=c or c<=b<=a:
# 「Yes」を出力
print("Yes")
# そうでなければ
else:
# 「No」を出力
print("No")
B - Distance Between Tokens Dif:57
駒の移動を行方向、列方向へ分けて考えましょう。
例えば駒がそれぞれ(1,5),(3,4)においてある場合
行方向:1→3=|1-3|=2の移動
列方向:5→4=|5-4|=1の移動
と計算できます。
一般に駒の座標が(x1,y1),(x2,y2)の場合
行方向:x1→x2=|x1-x2|の移動
列方向:y1→y2=|y1-y2|の移動
となりますから、これらを足せば答えになります。
駒の座標を特定するときはまず入力を1行ずつ受け取り、更にSを1文字ずつ「o」になっているか?と確認します。
駒の行、列を確認できたら配列へ格納してしまえばよいでしょう。
絶対値はabs(値)と書けば計算できます。
【提出】
# 入力の受け取り
H,W=map(int,input().split())
# 駒の座標格納用リスト
p=[]
# 行:G=0~(H-1)
for G in range(H):
# 入力の受け取り
S=input()
# 列:R=0~(W-1)
for R in range(W):
# SのR文字目が「o」ならば
if S[R]=="o":
# 座標を記録
p.append([G,R])
# 行方向の移動量
Gmove=abs(p[0][0]-p[1][0])
# 列方向の移動量
Rmove=abs(p[0][1]-p[1][1])
# 答えの出力
print(Gmove+Rmove)
C - Max - Min Query Dif:518
公式の想定解はC++のstd::multisetなのですがpythonにはこれにあたる機能が標準でありません。
残念ながらpythonではかなり遠回りした解法が必要になります。
考え方としては以下のようになります。
・defalutdictでそれぞれの数がSに入っている数を管理する
・heapで最大値、最小値を高速で取り出す
・defalutdictでそれぞれの数がSに入っている数を管理する
まずSにそれぞれの数がいくつ入っているかどのように管理するか考えます。リストに入れてcountで数えるではリストが長くなったときにTLEしますから、工夫がいります。
そこでdefalutdictを使います。
defaultdict(連想配列)について
辞書または連想配列と言います。
キー:値
というような対応付を行えるデータ構造です。
連想配列はdict()と書くことでも使えますが、デフォルトの値(初期値)が設定できません。そのため存在チェックなど色々面倒が発生します。
その面倒を避けるためにdefaultdictを使います。
import:from collections import defaultdict
作成(デフォルト0):変数名=defaultdict(int)
キー、値の登録:変数名[キー]=値
値の取り出し:変数名[キー]
【使用例】
# インポート
from collections import defaultdict
# 作成(デフォルト0):変数名=defaultdict(int)
dictionary=defaultdict(int)
# キー、値の登録:変数名[キー]=値
dictionary[5]=1
# 値の取り出し:変数名[キー]
x=dictionary[5]
詳しく知りたい人は以下を参照してください。
Countというdefalutdict(連想配列)を作り、数xがSにk個入っているなら
Count[x]=k
となるようにするわけです。例えばSに「1」が3個入っているならCount[1]=3です。
これならクエリ1でxを追加するときはCount[x]をプラス1すればいいし、クエリ2でxを取り出すときはCount[x]からmin(c,Sに含まれるxの個数(=Count[x]))を引けばO(1)で処理できるわけです。
・heapで最大値、最小値を高速で取り出す
リストから単純に最大値、最小値を探すのは計算量がO(リストの長さ)かかりますからやはりTLEします。
最小値、最大値を高速で取り出すと言えばheapです。
heapについて
heapはリストから最小値をO(logN)で取り出せるデータ構造です。
import:import heapq
リストのheap化 O(N):heapify(リスト)
要素の追加 O(logN):heappush(リスト,要素)
最小値の参照 O(1):リスト[0]
最小値の取り出し O(logN):heappop(リスト)
【使用例】
# インポート
import heapq
# リストを用意
que=list()
# リストのheap化 O(N):heapify(リスト)
heapq.heapify(que)
# 要素の追加 O(logN):heappush(リスト,要素)
heapq.heappush(que, 6)
heapq.heappush(que, 1)
# 最小値の参照 O(1):リスト[0]
print(que[0])
# 最小値の取り出し O(logN):heappop(リスト)
min_x=heapq.heappop(que)
詳しく知りたい人は以下のページを見てください。
まず「最小値を取り出す用」のheap que(MinQue)と「最大値を取り出す用」のheap que(MaxQue)を用意します。
xを受け取ると同時に両方のheap queへxをぶちこみます。ただしheap queは最小値しか取り出せませんから「最大値を取り出す用」のheap que(MaxQue)には「-x」をぶちこみます。
クエリ3が来たら最小値、最大値をそれぞれのMinQue、MaxQueから取り出します。
ただしMaxQueには「-x」の形で格納されているので取り出すときに(-1)を掛けてプラスにしましょう。
さて、取り出した最小値、最大値ですがクエリ2によってすでに全部削除されて0個になっているかもしれませんね。
そこでdefaultdictに記録した個数の出番です。取り出した最小値、最大値がまだあるか?をCountから確認します。
例えば取り出した最小値が「1」であった場合、Count[1]=0ならばもう「1」はSに入っていないので次の最小値をMinQueから取り出し直します。
まだある場合、つまり1≤Count[1]ならば「1」を最小値として記録した後、「1」をMinQueへ戻します。
最大値も同様です。
【提出】
# 入力の受け取り
Q=int(input())
# defaultdictのインポート
from collections import defaultdict
# それぞれの数がSにいくつ入っているか確認する連想配列
# 初期値は0
Count=defaultdict(int)
# heapqのインポート
import heapq
# 最大値を取り出す用
MaxQue=[]
# 最小値を取り出す用
MinQue=[]
# Q回
for i in range(Q):
# 入力の受け取り
# クエリの種類によって長さが違うからリストで受け取り
query=list(map(int,input().split()))
# クエリ1
if query[0]==1:
# xを確認
x=query[1]
# xがSに1個増えた
Count[x]+=1
# heap queへ入れる
heapq.heappush(MinQue,x)
# heap queは最小値しか取り出せないから最大値の方へは「-x」を入れる
heapq.heappush(MaxQue,-x)
# クエリ2
elif query[0]==2:
# x,cを確認
x=query[1]
c=query[2]
# Sからmin(c,Sに入っている個数)個のxを削除
Count[x]-=min(c,Count[x])
# クエリ3
else:
# Sの最小値を取り出し
SMin=heapq.heappop(MinQue)
# SMinが0個である場合
while Count[SMin]==0:
# 次の最小値を取り出し
SMin=heapq.heappop(MinQue)
# Sの最大値を取り出し
SMax=heapq.heappop(MaxQue)
# マイナスを取る⇔(-1)を掛ける
SMax*=-1
# SMaxが0個である場合
while Count[SMax]==0:
# 次の最大値を取り出す
SMax=heapq.heappop(MaxQue)
# マイナスを取る⇔(-1)を掛ける
SMax*=-1
# (最大値-最小値)を出力
print(SMax-SMin)
# 最小値、最大値をheap queへ戻す
heapq.heappush(MinQue,SMin)
heapq.heappush(MaxQue,-SMax)
D - FizzBuzz Sum Hard Dif:520
包除原理を使います。
包除原理なんて大層な名前がついていますが要するに高校数学でやる
(AまたはB)=A+B-(AかつB)
というやつです。
1~Nの和からAの倍数とBの倍数を引き算します。
例えば1~15の和から4の倍数と6の倍数を引くことを考えます。
1~15の和:1+2+3+4+5+6+7+8+9+10+11+12+13+14+15
4の倍数の和:4+8+12
6の倍数の和:6+12
このまま(1~15の和)-(4の倍数の和)-(6の倍数の和)と計算すると「12」を二重で引くことになってしまいますね。この「12」というのは4と6、つまりAとBの最小公倍数です。
よって答えは
(1~15の和)-(4の倍数の和)-(6の倍数の和)+(12の倍数の和)
となります。
一般には
(1~Nの和)-(Aの倍数の和)-(Bの倍数の和)+(AとBの最小公倍数の倍数の和)
となります。
それぞれの計算は等差数列の和ですから公式「(n/2)*(2a+(n-1)d)」(n:項数 a:初項 d:公差)で計算できます。
Aの倍数の和であれば項数は(N//A)となります。
ちなみにpythonでは最小公倍数を計算する機能はありませんが、最大公約数はmathのgcdで計算できます。A,Bの最小公倍数は(A*B)//(A,Bの最大公約数)で計算できます。
【提出】
# 最小公倍数の計算を行う関数
import math
def lcm(x, y):
return (x * y) // math.gcd(x, y)
# 入力の受け取り
N,A,B=map(int,input().split())
# 等差数列の和
# n:項数 a:初項 d:公差
def TousaSum(n,a,d):
return n*(2*a+(n-1)*d)//2
# 答え
# 1~Nまでの和
ans=TousaSum(N,1,1)
# Aの倍数の和を引く
ans-=TousaSum(N//A,A,A)
# Bの倍数の和を引く
ans-=TousaSum(N//B,B,B)
# 最小公倍数
ABlcm=lcm(A,B)
# A,Bの最小公倍数の和を引く
ans+=TousaSum(N//ABlcm,ABlcm,ABlcm)
# 答えの出力
print(ans)
E - Distance Sequence Dif:1073
DPで解きます。
DPとは「ある状態までの答えがわかっていれば→その次の状態の答えも出せる」という手続きを何度も行って最終的な答えを出す方法です。
DPの解説動画を作りましたので、本問が難しいと感じた方は是非御覧ください。
具体的な手順は以下です。
(1)表を作る
(2)すぐにわかるところを埋める
(3)表の小さい方から答えにたどり着くまで埋める
(4)答えを出力する
入力例として
N:4
M:9
K:3
を考えます。
(1)表を作る
今回作る表は「長さiの数列で末尾がxのものの個数」とします。名前はdpとします。

(2)すぐにわかるところを埋める
すぐにわかるのはi=1の行です。i=1ということは「長さ1の数列で末尾がxのものの個数」となります。
例えばdp[1][1]は長さ1で末尾が1ですから(1)の1個しかありません。
dp[1][2]は長さ1で末尾が2ですから(2)、dp[1][3]は同様に(3)、...とそれぞれ1個しかありません。
よってi=1の行はすべて1が入ります。
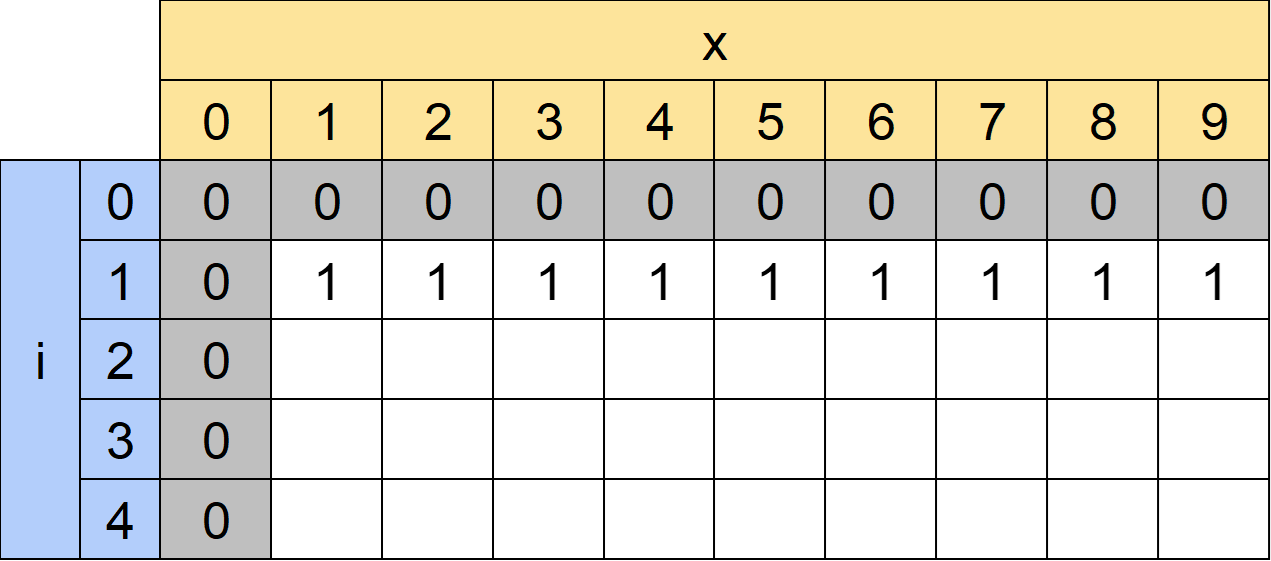
一般には以下のように表せます。
・(1≤x≤M)dp[1][x]=1
なお、i=0またはx=0の部分(灰色の部分)は長さ0、末尾0の数列となりますが便宜上0を入れておきます。
(3)表の小さい方から答えにたどり着くまで埋める
i=2の行を考えましょう。「長さ2の数列で末尾がxのものの個数」となります。
例えばdp[2][1]は「長さ2の数列で末尾が1のものの個数」となります。K=3ですから以下6個が考えられます。
(4,1)
(5,1)
(6,1)
(7,1)
(8,1)
(9,1)
同様にdp[2][2]は「長さ2の数列で末尾が2のものの個数」ですから以下5個が考えられます。
(5,2)
(6,2)
(7,2)
(8,2)
(9,2)
dp[2][3]も同じように考えると4個になります。
dp[2][4]はどうでしょうか。書き出してみると以下のようになります。
(1,4)
(7,4)
(8,4)
(9,4)
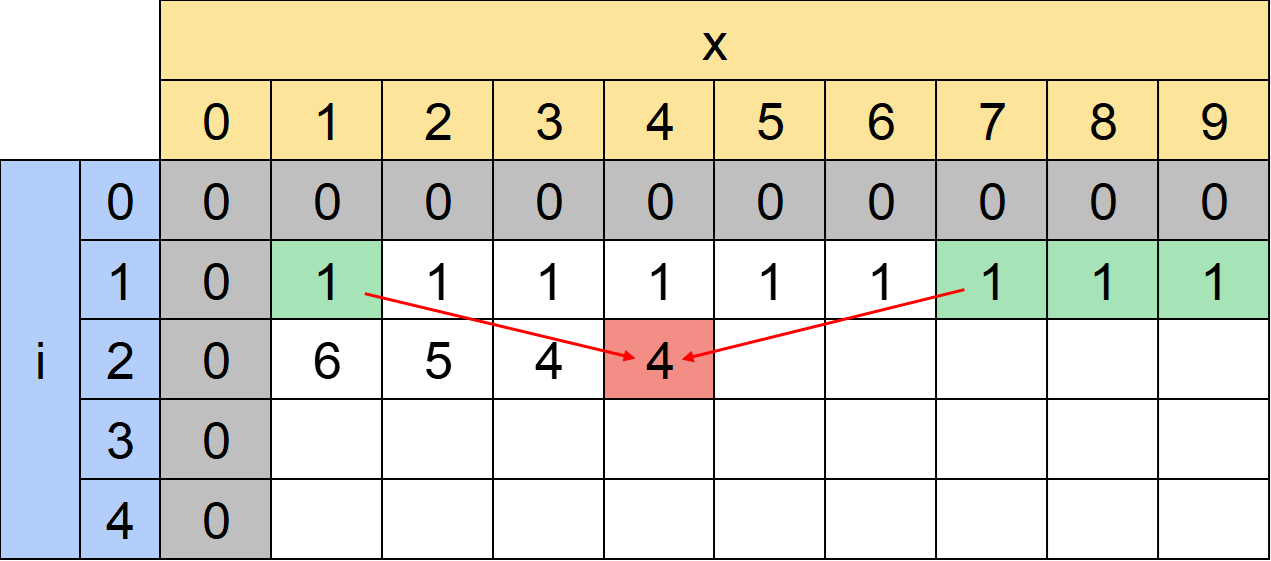
これは長さ1の数列(1)に「4」をくっつける、長さ1の数列(7)に「4」をくっつける、...という操作で作れることがわかります。
つまり長さ1の数列のうち、末尾(1項目)と4の差の絶対値がK以下であるものをもってきて「4」をくっつければいいわけです。
これは表でいうと緑の部分をすべて足すことに相当します。つまりdp[2][4]=dp[1][1]+dp[1][7]+dp[1][8]+dp[1][9]です。
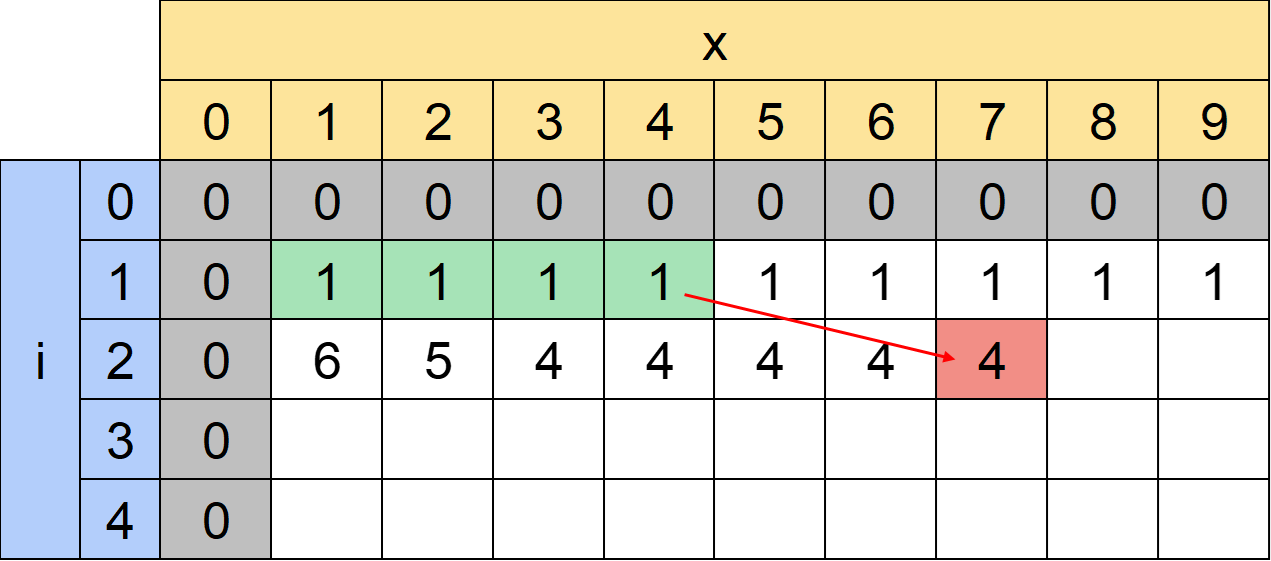
もう少し右側、例えばdp[2][7]であれば右側に差の絶対値がK以下であるものがないので以下のように左側だけ足す形になります。
一般には以下のように計算できます。
・(2≤i)dp[i][x]=(dp[i-1][1]+dp[i-1][2]+...+dp[i-1][x-K])+(dp[i-1][x+K]+dp[i-1][x+K+1]+...+dp[i-1][M])
ただしx-K<1(xが左側によっている場合)、またはM<x+K(xが右側によっている場合)のケースもあるので正確には以下のようになります。
・(2≤i,x-K<1)dp[i][x]=dp[i-1][x+K]+dp[i-1][x+K+1]+...+dp[i-1][M]
・(2≤i,M<x+K)dp[i][x]=dp[i-1][1]+dp[i-1][2]+...+dp[i-1][x-K]
・(2≤i,それ以外)dp[i][x]=(dp[i-1][1]+dp[i-1][2]+...+dp[i-1][x-K])+(dp[i-1][x+K]+dp[i-1][x+K+1]+...+dp[i-1][M])
これで表が埋まります・・・と言いたいところですがMが大きい場合、和の計算に時間がかかりすぎてTLEします。
要するに区間和が計算できればいいわけですから、i行目を計算するときに予め(i-1)行目の累積和(Cumulative sum)を計算しておきます。
例えばi=3行目を計算するときはi=2行目の累積和を予め計算しておきます。
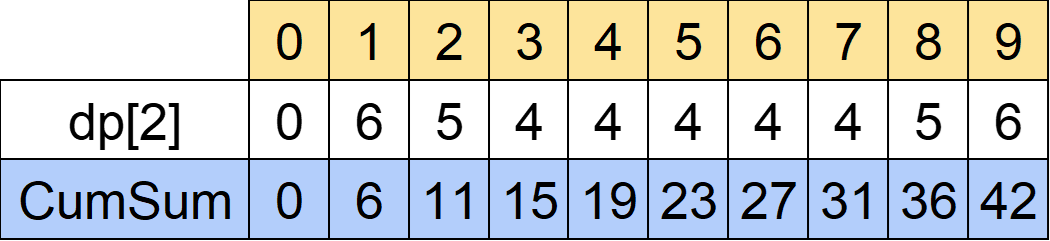
CumSum[x]はdp[2]のx番目までの和を意味します。
例えばCumSum[4]=dp[2][0]+dp[2][1]+dp[2][2]+dp[2][3]+dp[2][4]=0+6+5+4+4=19です。
実際に計算するときはx=1,2,3,...についてCumSum[x]=CumSum[x-1]+dp[i-1][x]とすればO(M)で計算できます。
累積和を使えばある区間の和は簡単に計算できます。
例えばdp[2][3]~dp[2][6]の和は
dp[2][3]~dp[2][6]の和=CumSum[6]-CumSum[3-1]=CumSum[6]-CumSum[2]=27-11=16
と計算できます。なぜこうなるかはCumSumの中身を書き下してみるとわかります。
CumSum[6]-CumSum[3-1]
=CumSum[6]-CumSum[2]
=(dp[2][0]+dp[2][1]+dp[2][2]+dp[2][3]+dp[2][4]+dp[2][5]+dp[2][6])-((dp[2][0]+dp[2][1]+dp[2][2])
=dp[2][3]+dp[2][4]+dp[2][5]+dp[2][6]
といい感じにいらないところが消えてくれます。
これで区間和の計算を前計算O(M)、一回あたりO(1)でできるようになりました。
後は計算を進めていくことで表を埋められます。
と、思ったらまだ終わりではありません。この問題は厄介なことにK=0のパターンが存在します。
K=0の場合
・(2≤i,それ以外)dp[i][x]=(dp[i-1][1]+dp[i-1][2]+...+dp[i-1][x-K])+(dp[i-1][x+K]+dp[i-1][x+K+1]+...+dp[i-1][M])
を計算するときにdp[i-1][x-K]とdp[i-1][x+K]が同じ値になってしまうので計算が合わなくなります。よってK=0の場合だけ特殊なケースとして
・(2≤i)dp[i][x]=dp[i-1][1]+dp[i-1][2]+...+dp[i-1][M]
と計算します。
これでようやっと表の計算ができます。一般化した式をまとめましょう。
・(1≤x≤M)dp[1][x]=1
K=0
・(2≤i)dp[i][x]=dp[i-1][1]+dp[i-1][2]+...+dp[i-1][M]
0<K
・(2≤i,x-K<1)dp[i][x]=dp[i-1][x+K]+dp[i-1][x+K+1]+...+dp[i-1][M]
・(2≤i,M<x+K)dp[i][x]=dp[i-1][1]+dp[i-1][2]+...+dp[i-1][x-K]
・(2≤i,それ以外)dp[i][x]=(dp[i-1][1]+dp[i-1][2]+...+dp[i-1][x-K])+(dp[i-1][x+K]+dp[i-1][x+K+1]+...+dp[i-1][M])
見づらいので累積和CumSumを使って書き直します。
・(1≤x≤M)dp[1][x]=1
K=0
・(2≤i)dp[i][x]=CumSum[M]
0<K
・(2≤i,x-K<1)dp[i][x]=CumSum[M]-CumSum[x+K-1]
・(2≤i,M<x+K)dp[i][x]=CumSum[x-K]
・(2≤i,それ以外)dp[i][x]=(CumSum[M]-CumSum[x+K-1])+CumSum[x-K]
なお、上記は「x-K<1かつM<x+K」の場合が入っておらず、厳密ではありません。(「x-K<1かつM<x+K」の場合、dp[i][x]=0となります)
ですが実装でそこまで考えて条件分岐を書くと面倒なので、以下のように条件を満たした場合だけ足し算するという形にするのが楽です。
if 1<=x-K:
dp[i][x]+=CumSum[x-K]
if x+K<=M:
dp[i][x]+=CumSum[M]-CumSum[x+K-1]
計算の途中で桁が大きくなるとTLEする可能性があるので、都度余りを取るように注意してください。
(4)答えを出力する
答えは長さNの数列の個数の和、すなわちdp[N][1]~dp[N][M]の和です。
計算して出力すれば終わりです。お疲れ様でした。
pythonでは間に合わないのでpypyで提出します。
【提出】
# pypyで提出
# 入力の受け取り
N,M,K=map(int,input().split())
# 余りの定義
Mod=998244353
# (1)表を作る
dp=[[0]*(M+1) for i in range(N+1)]
# (2)すぐにわかるところを埋める
# ・(1≤x≤M)dp[1][x]=1
# i=1~M
for i in range(1,M+1):
# 1を埋める
dp[1][i]=1
# (3)表の小さい方から答えにたどり着くまで埋める
# i=2~N
for i in range(2,N+1):
# 累積和の計算
CumSum=[0]*(M+1)
# x=1~M
for x in range(1,M+1):
CumSum[x]=CumSum[x-1]+dp[i-1][x]
CumSum[x]%=Mod
# x=1~M
for x in range(1,M+1):
# K=0
# ・(2≤i)dp[i][x]=CumSum[M]
if K==0:
dp[i][x]=CumSum[M]
# 0<K
else:
# ・(2≤i,x-K<1)dp[i][x]=CumSum[M]-CumSum[x+K-1]
# ・(2≤i,M<x+K)dp[i][x]=CumSum[x-K]
# ・(2≤i,それ以外)dp[i][x]=(CumSum[M]-CumSum[x+K-1])+CumSum[x-K]
# 条件を満たしている場合だけ足し算する
if 1<=x-K:
dp[i][x]+=CumSum[x-K]
if x+K<=M:
dp[i][x]+=CumSum[M]-CumSum[x+K-1]
# 余りを取る
dp[i][x]%=Mod
# (4)答えを出力する
# 答え
ans=0
# dp[N][1]~dp[N][M]の和
# x=1~M
for x in range(1,M+1):
ans+=dp[N][x]
# 余りを取る
ans%=Mod
# 答えの出力
print(ans)
【広告】
『AtCoder 凡人が『緑』になるための精選50問詳細解説』
AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段:100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/
【booth(pdf)】
https://sano192.booth.pm/items/3179185
1~24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf
『AtCoder ABC201~225 ARC119~128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』
ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV
【booth(pdf)】
https://booth.pm/ja/items/3698647
ARC119~128の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/
【booth(pdf)】
https://sano192.booth.pm/items/3698668
『AtCoder ABC226~250 ARC129~139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』
ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS
【booth(pdf)】
https://sano192.booth.pm/items/4025713
ARC129~139の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF
【booth(pdf)】
https://sano192.booth.pm/items/4025737
『Excelでリバーシを作ろう!! マクロ、VBAを1から学ぶ』
Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です!
マクロ、VBAが全くわからない人でも大丈夫! 丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます!
値段:300円(Kindle Unlimited対象)
サンプルとして「準備」~「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb
【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW
【booth(pdf】
https://sano192.booth.pm/items/3785312