Go to Qiita Advent Calendar 2024 Top
LoginSignup
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

More than 1 year has passed since last update.

@sano192

ABC243 A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

Last updated at Posted at 2022-03-13

ABC243(AtCoder Beginner Contest 243)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

A - Shampoo

実際にシャンプーがなくなるまで使ってみましょう。
シャンプーのもとの量がVで
父が使うとA
母が使うとB
高橋君が使うとC
減っていきます。

Vからそれぞれ引き算し、Vがマイナスになった時点で誰が使っていたのか確認します。

for i in range(最後の数):
と書くことでi=0~(最後の数-1)まで代入しながら処理が行なえます。
本問ではiの値はどうでもいいのですが、このように書くことで(最後の数)回の処理=「シャンプーを使う」ができるということです。
(最後の数)はとりあえず馬鹿みたいに大きい数を入れておきましょう。どうせシャンプーの残量がマイナスになった時点で終了するので処理回数が多くても問題ないです。
【提出】では(最後の数)=10^10にしています。

プログラムを途中終了する時は
exit()
と書きます。
シャンプーの残量がマイナスになった時点で答えを出力して終了します。

「F」「M」「T」は文字列なので出力の際、"F","M","T"とダブルクオーテーションをつけてください。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
V,A,B,C=map(int,input().split())

# シャンプーを使う
# i=0~(10^10)
for i in range(10**10):
    # 父が使う
    V-=A
    # 残量がマイナスになったら
    if V<0:
        # 「F」を出力
        print("F")
        # 途中終了
        exit()

    # 母が使う
    V-=B
    # 残量がマイナスになったら
    if V<0:
        # 「M」を出力
        print("M")
        # 途中終了
        exit()

    # 高橋君が使う
    V-=C
    # 残量がマイナスになったら
    if V<0:
        # 「T」を出力
        print("T")
        # 途中終了
        exit()

B - Hit and Blow

問題文の「言い換えると～」の部分を実装できればOKです。

  1. Ai=Biを満たす整数iの個数
    これはi=0~(N-1)についてA[i]=B[i]となる個数を数えればOKです。(pythonは0インデックスなのでA1=A[0],A2=A[1],...となることに注意してください)

  2. Ai=Bj,i≠jを満たす整数の組(i,j)の個数
    これはi=0~(N-1),j=0~(N-1)についてA[i]=B[j]かつi≠jとなる個数を数えればOKです。
    for i in range(N):
    　for j in range(N):
    と書くことで
    i=0についてj=0,1,2,...
    i=1についてj=0,1,2,...
    i=2についてj=0,1,2,...
    という順に処理ができます。
    i≠jという条件は「i!=j」と書きます。

【提出】

# 入力の受け取り
N=int(input())
A=list(map(int,input().split()))
B=list(map(int,input().split()))

# 1番目の答え
ans1=0

# i=0~(N-1)
for i in range(N):
    # A[i]=B[i]ならば
    if A[i]==B[i]:
        # カウント
        ans1+=1

# 答えを出力
print(ans1)

# 2番目の答え
ans2=0

# i=0~(N-1)
for i in range(N):
    # j=0~(N-1)
    for j in range(N):
        # A[i]=B[j] かつ i≠j ならば
        if A[i]==B[j] and i!=j:
            # カウント
            ans2+=1

# 答えの出力
print(ans2)

C - Collision 2

衝突するケースを考えましょう。
Y座標が同じ人のうち、「左に動く人」が「右に動く人」より右にいれば衝突します。
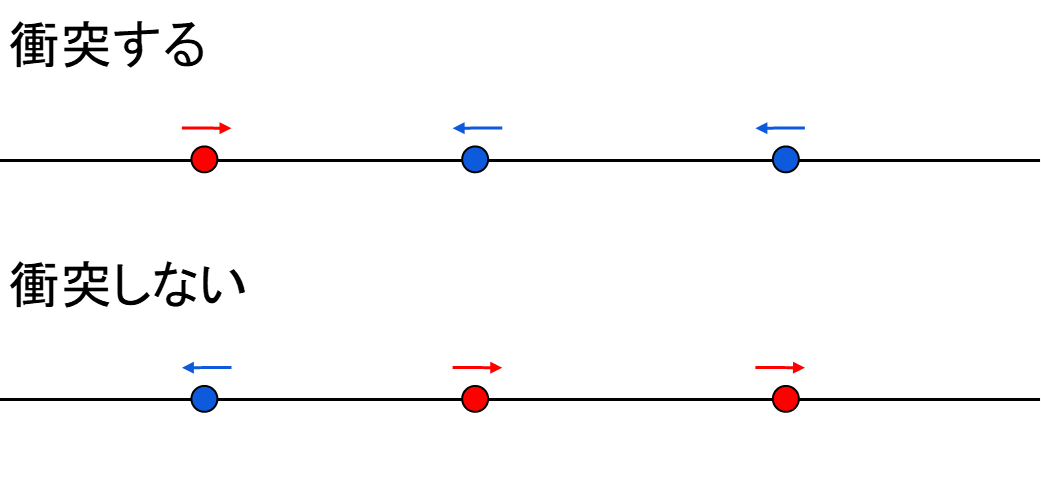
ABC242_C_1.png

つまり各Yについて1つでも以下が成り立てば衝突します。
「右に動く人のうち、最も左にいる人のx座標(最小のx座標)」<「左に動く人のうち、最も右にいる人のx座標(最大のx座標)」

各Y座標の「右に動く人のx座標」「左に動く人のx座標」の記録について考えましょう。
素朴にやるなら二次元配列を作ってY座標がyで「右に動く人」「左に動く人」を記録すればよさそうです。
例えばY座標が3のうち、「右に動く人のx座標」がそれぞれ2,4,5だったら
directionR[3]=[2,4,5]
とするわけです。
しかしYの制約が最大で10^9であるため、MLE(メモリ制限超過)します。
そこで連想配列(defaultdict)を使います。

defaultdict(連想配列)について
辞書または連想配列と言います。
キー：値
というような対応付を行えるデータ構造です。
連想配列はdict()と書くことでも使えますが、デフォルトの値(初期値)が設定できません。そのため存在チェックなど色々面倒が発生します。
その面倒を避けるためにdefaultdictを使います。
import：from collections import defaultdict
作成(デフォルト0)：変数名=defaultdict(int)
キー、値の登録：変数名[キー]=値
値の取り出し：変数名[キー]
【使用例】

# インポート
from collections import defaultdict

# 作成(デフォルト0)：変数名=defaultdict(int)
dictionary=defaultdict(int)

# キー、値の登録：変数名[キー]=値
dictionary[5]=1

# 値の取り出し：変数名[キー]
x=dictionary[5]

詳しく知りたい人は以下を参照してください。

「左に動く人のx座標」(=directL)
「右に動く人のx座標」(=directR)
を連想配列で記録していきます。
今回デフォルトの値は空のリストにしたいため、
変数名=defaultdict(list)
と書きます。

座標の入力を受け取る時、y座標をsetに記録しておきます。
こうすることで人がいるy座標の一覧を作ることが出来ます。

あとは人がいるy座標のそれぞれについて、
・「右に動く人のうち、最も左にいる人のx座標(最小のx座標)」<「左に動く人のうち、最も右にいる人のx座標(最大のx座標)」であれば
　→衝突
というように条件を確認できます。

【提出】

# 入力の受け取り
N=int(input())

# 座標
p=[]
# 人がいるy座標の記録セット
y_set=set()
# N回
for i in range(N):
    # 入力の受け取り
    X,Y=map(int,input().split())
    # 座標を記録
    p.append([X,Y])
    # y座標を記録
    y_set.add(Y)

# 入力の受け取り
S=input()

# defaultdictをインポート
from collections import defaultdict

# 左に動く人のx座標の記録
directL=defaultdict(list)
# 右に動く人のy座標の記録
directR=defaultdict(list)

# i=0~(N-1)
for i in range(N):
    # 人iのx,y座標
    x,y=p[i]
    # S[i]が「L」ならば
    if S[i]=="L":
        # 左に動く人として記録
        directL[y].append(x)
    # そうでなければ(S[i]が「R」ならば)
    else:
        # 右に動く人として記録
        directR[y].append(x)

# 各yについて
for y in y_set:
    # 左に動く人と右に動く人がそれぞれ1人以上いれば
    if 1<=len(directL[y]) and 1<=len(directR[y]):
        # 「右に動く人のうち、最も左にいる人のx座標(最小のx座標)」<「左に動く人のうち、最も右にいる人のx座標(最大のx座標)」
        if min(directR[y])<max(directL[y]):
            # 「Yes」を出力
            print("Yes")
            # 終了
            exit()

# 「No」を出力
print("No")

D - Moves on Binary Tree

Nはそこまで大きくないので普通にシミュレーションすれば解けそう・・・ですがこれは失敗します。
例えば最初頂点1にいて、「L」が1000回続けば移動後は2^1000にたどり着くことになります。さすがに桁が大きすぎて計算が間に合いません。

Sについて「LU」や「RU」がある場合、その間の移動は
子に移動→親に戻る
なので実質的に移動していないとの同じことになります。よってこの移動は無視して構いません。
具体的には例えば
S=ULURULRULU
⇔S=U(LU)(RU)L(RU)(LU)
⇔S=UL
となります。

よって以下のように実装します。
「実質的な移動」をmoveに記録する。
i=0,1,2,...について
・moveが空→S[i]を記録
・moveが空でない
　・S[i]が「L」または「R」→S[i]を記録
　・S[i]が「U」 かつ moveの右端が「L」または「R」→moveの右端を消す
　・S[i]が「U」 かつ moveの右端が「U」→「U」を記録

あとはmoveの文字を確認しながらシミュレーションを行えば終わりです。

【提出】

# 入力の受け取り
N,X=map(int,input().split())
S=input()

# 移動の記録
move=[]

# i=0~(N-1)
for i in range(N):
    # ・moveが空
    if len(move)==0:
        # S[i]を記録
        move.append(S[i])
    
    # ・moveが空でない
    else:
        # ・S[i]が「L」または「R」
        if S[i]=="L" or S[i]=="R":
            # S[i]を記録
            move.append(S[i])
        # ・S[i]が「U」
        else:
            # ・moveの右端が「L」または「R」
            if move[-1]=="L" or move[-1]=="R":
                # 右端を消す
                move.pop()
            # ・moveの右端が「U」
            else:
                # 「U」を記録
                move.append("U")

# シミュレーション
for s in move:
    # 「L」ならば2Xへ移動
    if s=="L":
        X*=2
    # 「R」ならば(2X+1)へ移動
    elif s=="R":
        X=2*X+1
    # 「U」ならばX//2へ移動
    else:
        X//=2

# 答えの出力
print(X)

【広告】

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312

0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?