エイシングプログラミングコンテスト2022(ABC255) A～D問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

ABC255(AtCoder Beginner Contest 255)　A～D問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

エイシング様について

エイシング様は、2016年に設立されたスタートアップで、AIの開発を行っています。
興味のある方は公式ホームページを御覧ください。

A - You should output ARC, though this is ABC.　Dif:13

R,Cの組み合わせは(1,1),(1,2),(2,1),(2,2)の4パターンしかありません。
これくらいなら全パターンifで条件分岐してしまえばOKです。

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出】

# 入力の受け取り
R,C=map(int,input().split())
A11,A12=map(int,input().split())
A21,A22=map(int,input().split())

# (R,C)=(1,1)の場合
if R==1 and C==1:
    # 答えの出力
    print(A11)
# (R,C)=(1,2)の場合
elif R==1 and C==2:
    # 答えの出力
    print(A12)
# (R,C)=(2,1)の場合
elif R==2 and C==1:
    # 答えの出力
    print(A21)
# (R,C)=(2,2)の場合
elif R==2 and C==2:
    # 答えの出力
    print(A22)

B - Light It Up　Dif:351

もし明かりを持っている人が一人だけなら答えはその人から一番遠い人までの距離となります。
と、いうことは複数人いるなら明かりを持っている人それぞれと全員との距離を計算し、必要な半径を計算すればよいです。
これは表にして確認することでよりわかりやすくなります。

「例」
N K：5 3
A：1 3 5
X1 Y1：0 0
X2 Y2：5 5
X3 Y3：2 4
X4 Y4：6 6
X5 Y5：5 8

明かりを持っている人は人1、人3、人5です。これを行方向に、他の人を列方向にとってそれぞれの距離を計算します。

例えば(行,列)=(3,4)の部分は人3と人4の距離を表します。
X3 Y3：2 4
X4 Y4：6 6
距離は√((2-6)^2+(4-6)^2)=√(16+4)=4.47...となるわけです。

この表を列方向へ確認しましょう。1列目なら人1を照らすのに必要な距離がそれぞれ書いているわけですから、そのうち一番小さい半径が答えの候補になります。
同様にそれぞれの列について最も小さい値を書いてみます。

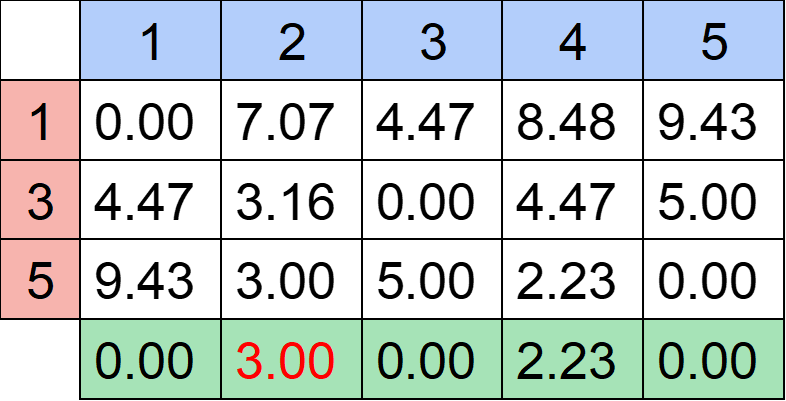
このうち一番大きいのは2列目の3.00です。
つまり人2を照らすには最低でもR=3.00が必要ということがわかります。
一般には(列ごとの最小値)の最大値が答えになります。

表を作るには二次元配列を作ります。
配列名=[[初期値]*(列数) for i in range(行数)]
と書くことで二次元配列を作れます。ただしこのままでは0インデックスとなり、ちょっとややこしいので実装では
dist=[[0]*(N+1) for i in range(K)]
と、行数を(N+1)としています。

値を更新したり取り出したりするときは
配列名[行][列]
と書きます。

ルートの計算は
from math import sqrt
と書くことでsqrt(数値)として(数値)のルートが計算できます。

【提出】

# 入力の受け取り
N,K=map(int,input().split())
A=list(map(int,input().split()))

# 座標の格納リスト
# 0番目を埋めるために[0,0]を入れておく
p=[[0,0]]

# N回
for i in range(N):
    # 入力の受け取り
    x,y=map(int,input().split())
    # 座標の記録
    p.append([x,y])

# 表を作る
dist=[[0]*(N+1) for i in range(K)]

# ルートの計算のためmathからsqrtをインポート
from math import sqrt

# 人aと人bの距離の計算関数
def CalcDist(a,b):
    return sqrt((p[a][0]-p[b][0])**2+(p[a][1]-p[b][1])**2)

# 行：Gyou=0~(K-1)
for Gyou in range(K):
    # 列：Retu=1~N
    for Retu in range(1,N+1):
        # 距離を計算して表を更新
        dist[Gyou][Retu]=CalcDist(A[Gyou],Retu)

# それぞれの列の最小値を確認するリスト
RetuMin=[0]*(N+1)

# 列：Retu=1~N
for Retu in range(1,N+1):
    # 距離
    d=10**10
    # 行：Gyou=0~(K-1)
    for Gyou in range(K):
        # d=ここまでのdと表の値の小さい方
        d=min(d,dist[Gyou][Retu])
    
    # 最小値を記録
    RetuMin[Retu]=d

# (列ごとの最小値)の最大値
print(max(RetuMin))

C - ±1 Operation 1　Dif:574

要するにXがSのどの要素の間にあるかわかればいいわけです。
例えば
X：5
S：1 4 7 11
であればXは4と7の間にあります。Xを4にするには操作1回、7にするには操作2回が必要なので小さい方の1回が答えとわかります。
しかし制約Nが大きいので、Xがどの要素の間にあるかSの小さい方から順に確かめていくとTLEします。
そこで二分探索を使います。

二分探索
二分探索は区間の中央の値が条件を満たすか確認し、徐々に区間を狭めて目的の値を得るアルゴリズムです。
探索を行う前に対象の数列は単調増加、または減少となっている必要があります。
(1)区間[左,右]を指定する
左端=最小値(単調減少なら最大値)のインデックス番号
右端=最大値(単調減少なら最小値)のインデックス番号
(2)中央=(左+右)//2が条件を満たすか確認
(3)(2)の結果より左または右を更新する
　・中央が条件を満たす：右(または左)=中央と更新
　・中央が条件を満たさない：左(または右)=中央と更新
(4)1<(右-左)となっている間(2)~(4)を繰り返す

Dの値がプラスの場合はX以下の値のうち、最大のものが何番目にあるか確認します。
Dの値がマイナスの場合はX以上の値のうち、最小のものが何番目にあるか確認します。

「例」
X：7
A D N：1 2 7
Sを作ってみると以下のようになります。
S：1 3 5 7 9 11 13

(1)区間[左,右]を指定する
　左=0
　右=7(項数N)
(2)中央=(左+右)//2が条件を満たすか確認
　左=0
　右=7
　中央=(0+7)//2=3
　S(3)=5
(3)(2)の結果より左または右を更新する
　5≤7(=X)です。この場合は左=中央(=3)と更新します。
(4)1<(右-左)となっている間(2)~(4)を繰り返す
　右-左=7-3=4です。(2)へ戻ります。

(2)中央=(左+右)//2が条件を満たすか確認
　左=3
　右=7
　中央=(3+7)//2=5
　S(5)=9
(3)(2)の結果より左または右を更新する
　7(=X)<9です。この場合は右=中央(=5)と更新します。
(4)1<(右-左)となっている間(2)~(4)を繰り返す
　右-左=7-5=2です。(2)へ戻ります。

(2)中央=(左+右)//2が条件を満たすか確認
　左=3
　右=5
　中央=(3+5)//2=4
　S(4)=7
(3)(2)の結果より左または右を更新する
　7≤7(=X)です。この場合は左=中央(=4)と更新します。
(4)1<(右-左)となっている間(2)~(4)を繰り返す
　ここで右-左=5-4=1となり終了です。

結局XはS(4)=7とS(5)=9の間にあるということがわかります。
よって7-7=0と9-7=2の小さい方、0回の操作でXを「良い数」にすることができます。

Dがマイナスのときは『(3)(2)の結果より左または右を更新する』の部分を逆に処理する二分探索が必要になります。
公式解説にある通りDをプラスに変えても答えは変わらないので、2つ二分探索を書くのが面倒ならそのようにしてもよいです。

【提出】

# 入力の受け取り
X,A,D,N=map(int,input().split())

# Sのi項目を計算する関数
def S(i):
    return A+(i-1)*D

# Dがプラスの場合の二分探索
def NibutanPlus(X):

    # (1)区間[左,右]を指定する
    l=0
    r=N

    # (4)1<(右-左)となっている間(2)~(4)を繰り返す
    while 1<r-l:
        # (2)中央=(左+右)//2が条件を満たすか確認
        # (3)(2)の結果より左または右を更新する
        c=(l+r)//2

        if S(c)<=X:
            # 左=中央と更新
            l=c
        else:
            # 右=中央と更新
            r=c

    # l,rを返す
    return l,r

# Dがマイナスの場合の二分探索
def NibutanMinus(X):
    l=0
    r=N

    while 1<r-l:
        c=(l+r)//2

        if S(c)<=X:
            r=c
        else:
            l=c

    return l,r

# Dが0の場合
if D==0:
    # |A-X|が答え
    print(abs(A-X))

# Dがプラスの場合
elif 0<D:
    # Xが初項より小さい場合
    if X<A:
        # (A-X)が答え
        print(A-X)
    # Xが末項より大きい場合
    elif S(N)<=X:
        # (X-末項)が答え
        print(X-S(N))
    # 上記以外
    else:
        # 二分探索でどの項の間にあるか確認
        l,r=NibutanPlus(X)
        # 差が小さいほうが答え
        print(min(X-S(l),S(r)-X))

# Dがマイナスの場合
else:
    # Xが初項より大きい場合
    if A<X:
        # (X-A)が答え
        print(X-A)
    # Xが末項より小さい場合
    elif X<=S(N):
        # (末項-X)が答え
        print(S(N)-X)
    # それ以外
    else:
        # 二分探索でどの項の間にあるか確認
        l,r=NibutanMinus(X)
        # 差が小さいほうが答え
        print(min(S(l)-X,X-S(r)))

D - ±1 Operation 2　Dif:788

Aの各要素とXの差の絶対値の合計が答えになりますが、一個一個計算していたら当然TLEします。
以下の例を考えます。
A：6 11 2 5 5
X：5

とりあえずAをソートしましょう。数列が出てきたときにソートしても答えが変わらないならとりあえずソートしてみるというのは有効な場合が多いです。
A：2 5 5 6 11

AをX以下の部分とXより大きい部分に分けて考えます。
・X以下の部分
2 5 5の部分です。
(X-2)+(X-5)+(X-5)=(5-2)+(5-5)+(5-5)=3+0+0=3
よって3回の操作が必要なことがわかります。
式変形すると
(X-2)+(X-5)+(X-5)=3*X-(2+5+5)=3*X-(A1~A3の和)
となります。なんか解けそうな気がしてきましたね。

・Xより大きい部分
6 11の部分です。
(6-X)+(11-X)=(6-5)+(11-5)=1+6=7
よって7回の操作が必要なことがわかります。
式変形すると
(6-X)+(11-X)=(6+11)-2*X=(A4~A5の和)-2*X
となります。

要するにXがAlとA(l+1)の間にあるなら操作回数は
(X*l-(A1~Alの和))+(A(l+1)~ANの和)-X*(N-l))
となるというわけです。

区間の和は累積和を使って求めます。

区間和(累積和による)
予め累積和を計算しておくことで区間和をO(1)で計算することができます。
Aの累積和(Cumulative sum)をACumとすると区間[l,r]の和はACum[r]-ACum[l-1]と計算できます。
累積和は以下のように計算することでO(N)で計算できます。
i=1,2,3,...,Nについて
ACum[i]=A_cum[i-1]+A[i]
※A[0]=0で埋めておきます

「例」
A：1 3 5 7 9 11 13 15 について区間[3,5]の和を求める場合
まず累積和を求めます。ACum[x]はA[1]~A[x]までの和を意味します。
例えばACum[3]=A[1]+A[2]+A[3]=1+3+5=9です。

ACum[2]=4
ACum[5]=25
ですので区間[3,5]の和は
ACum[5]-ACum[3-1]=ACum[5]-ACum[2]=25-4=21
となります。
なぜこのように計算できるかはACumを開いてみるとわかりやすいです。
ACum[5]-ACum[2]
=(A[1]+A[2]+A[3]+A[4]+A[5])-(A[1]+A[2])
=A[3]+A[4]+A[5]
と、いい感じにいらないところを引き算できるというわけです。

XがAのどの要素の間にあるかは二分探索で確認します。

二分探索
二分探索は区間の中央の値が条件を満たすか確認し、徐々に区間を狭めて目的の値を得るアルゴリズムです。
探索を行う前に対象の数列は単調増加、または減少となっている必要があります。
(1)区間[左,右]を指定する
左端=最小値(単調減少なら最大値)のインデックス番号
右端=最大値(単調減少なら最小値)のインデックス番号
(2)中央=(左+右)//2が条件を満たすか確認
(3)(2)の結果より左または右を更新する
　・中央が条件を満たす：右(または左)=中央と更新
　・中央が条件を満たさない：左(または右)=中央と更新
(4)1<(右-左)となっている間(2)~(4)を繰り返す

本問ではX以下の値のうち最大のものが何番目にあるか確認します。
「例」
X：5
A：1 2 3 4 5 6 7 8

(1)区間[左,右]を指定する
　左=1
　右=8(=N)
　※累積和を計算する都合上Aの受け取り時にA[0]をてきとうな値で埋めておき、1インデックスにすると楽です。
(2)中央=(左+右)//2が条件を満たすか確認
　左=1
　右=8
　中央=(1+8)//2=4
　A[4]=4
(3)(2)の結果より左または右を更新する
　4≤5(=X)です。この場合は左=中央(=4)と更新します。
(4)1<(右-左)となっている間(2)~(4)を繰り返す
　右-左=8-4=4です。(2)へ戻ります。

(2)中央=(左+右)//2が条件を満たすか確認
　左=4
　右=8
　中央=(4+8)//2=6
　A[6]=6
(3)(2)の結果より左または右を更新する
　5(=X)<6です。この場合は右=中央(=6)と更新します。
(4)1<(右-左)となっている間(2)~(4)を繰り返す
　右-左=6-4=2です。(2)へ戻ります。

(2)中央=(左+右)//2が条件を満たすか確認
　左=4
　右=6
　中央=(4+6)//2=5
　A[5]=5
(3)(2)の結果より左または右を更新する
　5≤5(=X)です。この場合は左=中央(=5)と更新します。
(4)1<(右-左)となっている間(2)~(4)を繰り返す
　ここで右-左=6-5=1となり終了です。

よってX以下の値のうち最大のものが5番目にあるということがわかります。
要するにXはA[5]とA[6]の間にあるということです。

あとは計算するだけです。もう一度計算式を思い出しましょう。
XがAlとA(l+1)の間にあるなら操作回数は
(X*l-(A1~Alの和))+(A(l+1)~ANの和)-X*(N-l)

l=5ですから以下のようになります。
=(5*5-(A1~A5の和))+(A(5+1)~A8の和)-5*(8-5)
=25-15+21-15
=16

【提出】

# 入力の受け取り
N,Q=map(int,input().split())
# A[0]を埋めておき、1インデックスにする
A=[0]+list(map(int,input().split()))

# Aをソート
A.sort()

# 二分探索
def Nibutan(X):
    # (1)区間[左,右]を指定する
    l=1
    r=N

    # (4)1<(右-左)となっている間(2)~(4)を繰り返す
    while 1<r-l:
        # (2)中央=(左+右)//2が条件を満たすか確認
        # (3)(2)の結果より左または右を更新する
        c=(l+r)//2

        if A[c]<=X:
            l=c
        else:
            r=c

    # 左端を返す
    return l

# 累積和の計算
ACum=[0]*(N+1)
for i in range(1,N+1):
    ACum[i]=ACum[i-1]+A[i]

# Q回
for i in range(Q):
    # 入力の受け取り
    X=int(input())

    # X<A1なら
    if X<A[1]:
        # (A1~ANの和)-X*N
        ans=ACum[N]-X*N
    # AN≤Xなら
    elif A[N]<=X:
        # X*N-(A1~ANの和)
        ans=X*N-ACum[N]
    # 上記以外
    else:
        # Xが何番目の要素の間にあるか確認
        l=Nibutan(X)

        # (X*l-(A1~Alの和))+(A(l+1)~ANの和)-X*(N-l)
        ans=X*l-ACum[l]+(ACum[N]-ACum[l])-X*(N-l)

    # 答えの出力
    print(ans)

【広告】

『AtCoder 最速で緑になる 基礎・典型50問詳細解説』

ABC201～250から基礎・典型問題50問をとてつもなく丁寧かつ詳細に解説した本(kindle)、pdf(booth)です。
灰色、茶色コーダーにおすすめ！
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BBB7RKTP

【booth(pdf)】
https://booth.pm/ja/items/4102300

冒頭5問をサンプルとして無料公開しています
https://qiita.com/sano192/items/6361ed72106cb6dd5843

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312