日鉄ソリューションズプログラミングコンテスト2022(ABC257) A～C問題 ものすごく丁寧でわかりやすい解説 python 灰色～茶色コーダー向け #AtCoder

日鉄ソリューションズプログラミングコンテスト2022(AtCoder Beginner Contest 257)　A～C問題の解説記事です。
灰色～茶色コーダーの方向けに解説しています。

その他のABC解説、動画などは以下です。

更新時はツイッターにて通知します。
https://twitter.com/AtCoder4

日鉄ソリューションズ(NSSOL)様について

本コンテストは日鉄ソリューションズ(NSSOL)様が主催されています。

A - A to Z String 2　Dif:22

実際に「A」をN個、「B」をN個、...と文字列を作ってしまいましょう。
例えば(文字列)に「A」をN個くっつけるときは
(文字列)+="A"*N
となります。

そうしてからX番目の文字を出力します。ただしpythonでは先頭を0文字目、次を1文字目、...と数えるのでX文字目=S[X-1]と1個ずれることに注意してください。
【提出1】

さすがに26行書くのはめんどくせえという人はchrを使いましょう。
文字には文字コードという番号が振られています。
「A」の文字コードは65
「B」の文字コードは66
...
「Z」の文字コードは90
です。

chr(数字)とすることで数字→文字コードと変換ができます。
i=65~90まで順に代入してchr(i)をくっつけていけば同様に文字を作ることができます。
【提出2】

入力の受け取り、出力がわからない方は以下の記事を参考にしてください。

【提出1】

# 入力の受け取り
N,X=map(int,input().split())

# 空の文字列を用意
S=""

# 「A」をN個くっつける
S+="A"*N
# 「B」をN個くっつける
S+="B"*N
S+="C"*N
S+="D"*N
S+="E"*N
S+="F"*N
S+="G"*N
S+="H"*N
S+="I"*N
S+="J"*N
S+="K"*N
S+="L"*N
S+="M"*N
S+="N"*N
S+="O"*N
S+="P"*N
S+="Q"*N
S+="R"*N
S+="S"*N
S+="T"*N
S+="U"*N
S+="V"*N
S+="W"*N
S+="X"*N
S+="Y"*N
S+="Z"*N

# 答えを出力
print(S[X-1])

【提出2】

# 入力の受け取り
N,X=map(int,input().split())

# 空の文字列を用意
S=""

# i=65~90
for i in range(65,91):
    # (文字コードi)の文字をN個くっつける
    S+=chr(i)*N

# 答えを出力
print(S[X-1])

B - 1D Pawn　Dif:91

実際にマス目を用意して駒を置いてみましょう。
マス目をSとします。
S[i]=0ならば駒が置いていない
S[i]=1ならば駒が置いている
とします。

まずAの情報からマス目に駒を置きます。
A[0],A[1],A[2],...のマス目には駒が存在しますから、i=0~(K-1)についてS[A[i]]=1とすればOKです。

次にLの情報から駒を動かしていきます。
まずL[i]番目の駒がどこにあるか確認しましょう。1番目のマス、2番目のマス、...と順にマス目を確認し、駒があればカウントします。
カウントがL[i]になったらそれがL[i]番目の駒があるマスです。そのマスをNowとします。

Nowが一番右のマスである場合はNow=Nとなります。逆に1番右のマスでないならNow<Nです。
Nowの右隣のマスに駒がない場合はS[Now+1]=0です。

以上より駒を右に動かす条件は
Now<N　かつ　S[Now+1]=0
となります。この場合だけ駒を右に動かします。具体的には
S[Now]は駒がなくなる⇔S[Now]=0
S[Now+1]に駒が移動する⇔S[Now+1]=1
となります。

移動が終わったら駒のあるマスを再度確認します。
i=1~Nについて
S[i]=1ならば駒がある⇔iを記録する
としていきます。

最後に記録したマス目を出力します。
print(*(リスト))
とすることでリストの[]なしで出力することができます。

【提出】

# 入力の受け取り
N,K,Q=map(int,input().split())
A=list(map(int,input().split()))
L=list(map(int,input().split()))

# Nマスのマス目を用意
# 0ならば駒がない
# 1ならば駒がある
S=[0]*(N+1)

# i=0~(K-1)
for i in range(K):
    # A[i]番目のマスに駒を置く
    S[A[i]]=1

# i=0~(Q-1)
for i in range(Q):
    # 何番目の駒か数える
    Count=0
    
    # Now=1~N
    # Now=今確認しているマス目
    for Now in range(1,N+1):
        # もしマス目Nowに駒が置いてあれば
        if S[Now]==1:
            # カウントする
            Count+=1
            # もしL[i]番目の駒ならば
            if Count==L[i]:
                # もしNow<N(一番右のマスでない)　かつ　1つ右のマスに駒がないならば
                if Now<N and S[Now+1]==0:
                    # 一つ右に駒を移動
                    S[Now+1]=1
                    # もとのマスに駒はなくなる
                    S[Now]=0
                    # 次のiへ
                    break

# 答え
ans=[]

# i=1~N
for i in range(1,N+1):
    # i番目のマスに駒があれば
    if S[i]==1:
        # 答えに追加
        ans.append(i)

# 答えの出力
# (「*」をつけると[]なしで出力できる)
print(*ans)

C - Robot Takahashi　Dif:678

大人と子どもを分けて、Xについてどの値がいいのかを考えていきます。
例を見ましょう。

S：101010
W：30 20 10 25 50 30

まず大人と子どもを分けて更に小さい順にソートします。

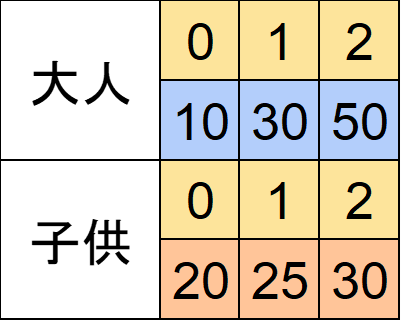
大人側から考えます。
Xの候補は10,20,30です。

(1)X=10
X=10の場合、大人側では3人を正しく判定できます。
これは大人リストの長さ=3から「10」のインデックス番号0を引いて3-0=3人と計算できます。

子供側は一番小さい人が20なので正しく判定できる人は0人です。
合計で3+0=3人を正しく判定できます。

(2)X=30
X=30の場合、大人側では2人を正しく判定できます。
同様に大人リストの長さ=3から「30」のインデックス番号1を引いて3-1=2人と計算できます。

子供側は20,25の2人を正しく判定できます。
合計で2+2=4人を正しく判定できます。

(3)X=50
X=50の場合、大人側では1人を正しく判定できます。
同様に大人リストの長さ=3から「50」のインデックス番号2を引いて3-2=1人と計算できます。

子供側はどうでしょうか。
ここで重要なことはXはどんどん大きくなっていくため、さっきX=30で正しく判定できた20,25の人はX=50でも確実に正しく判定できるということです。
つまりさっき正しく判定できた20,25の2人は確定で、2番目の30の人を正しく判定できるかだけ確認すればよいということです。
30の人も正しく判定できます。
合計で1+3=4人を正しく判定できます。

では次に子供側を考えましょう。
今度は子供リスト、大人リストを大きい順にソートします。

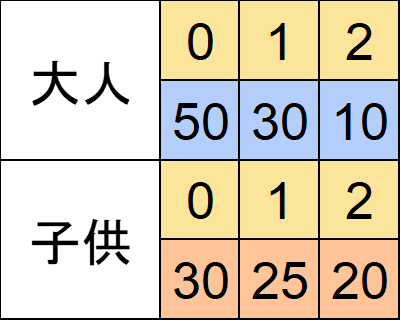
X未満を子供と判定するため、X=30,25,20とすると正しく判定してくれません。
そこで0.1ずつプラスしてX=30.1,25.1,20.1を候補とします。

(1)X=30.1
X=30.1の場合、子供側では3人を正しく判定できます。
これは子供リストの長さ=3から「30」のインデックス番号0を引いて3-0=3人と計算できます。

大人側は50の人のみ正しく判定できて1人です。
合計で3+1=4人を正しく判定できます。

(2)X=25.1
X=25.1の場合、子供側では2人を正しく判定できます。
同様に子供リストの長さ=3から「25」のインデックス番号1を引いて3-1=2人と計算できます。

今度はXはどんどん小さくなっていくため、X=30.1で正しく判定できた50の人はX=25.1でも確実に正しく判定できます。
つまりさっき正しく判定できた50の1人は確定で、1番目の30の人を正しく判定できるかだけ確認すればよいです。
30の人も正しく判定できます。
合計で2+2=4人を正しく判定できます。

(3)X=20.1
X=20.1の場合、子供側では1人を正しく判定できます。
同様に子供リストの長さ=3から「20」のインデックス番号2を引いて3-2=1人と計算できます。

同様に考えてX=25.1で正しく判定できた50,30の2人はX=20.1でも確実に正しく判定できます。
2番目の10の人は正しく判定できません。

合計で1+2=3人が正しく判定できます。

正しく判定できた人の最大は4人でしたから、答えは4となります。

【提出】

# 入力の受け取り
N=int(input())
S=input()
W=list(map(int,input().split()))

# 子供リスト
Child=[]
# 大人リスト
Adult=[]

# i=0~(N-1)
for i in range(N):
    # 子供なら
    if S[i]=="0":
        # 子供リストへ追加
        Child.append(W[i])
    # 大人なら
    else:
        # 大人リストへ追加
        Adult.append(W[i])

# リストの長さを確認
Clen=len(Child)
Alen=len(Adult)

# 答え
Ans=0

# ソート
Child.sort()
Adult.sort()

# 正しい判定をされる子供の人数
k=0
# i=0~(Adultの長さ)
for i in range(Alen):
    # X=大人の小さい方からi人目
    X=Adult[i]
    # 正しい判定をされる大人の人数
    tmpAns=Alen-i

    # k<(子供リストの長さ)　かつ　小さい方からk番目の子供<Xならば
    while k<Clen and Child[k]<X:
        # 正しい判定をされる子供の人数をカウント
        k+=1
    
    # 正しい判定をされる子供の人数をプラス
    tmpAns+=k

    # これまでの答えより多ければ答えを更新
    Ans=max(Ans,tmpAns)

# 大きい順にソートし直す
Adult.sort(reverse=True)
Child.sort(reverse=True)

# 正しい判定をされる大人の人数
k=0
# i=0~(Childの長さ)
for i in range(Clen):
    # X=子供の大きい方からi人目+0.1
    X=Child[i]+0.1
    # 正しい判定をされる子供の人数
    tmpAns=Clen-i

    # k<(大人リストの長さ)　かつ　大きい方からk番目の大人≤Xならば
    while k<Alen and X<=Adult[k]:
        # 正しい判定をされる大人の人数をカウント
        k+=1
    
    # 正しい判定をされる大人の人数をプラス
    tmpAns+=k

    # これまでの答えより多ければ答えを更新
    Ans=max(Ans,tmpAns)

# 答えの出力
print(Ans)

【広告】

『AtCoder 最速で緑になる 基礎・典型50問詳細解説』

ABC201～250から基礎・典型問題50問をとてつもなく丁寧かつ詳細に解説した本(kindle)、pdf(booth)です。
灰色、茶色コーダーにおすすめ！
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BBB7RKTP

【booth(pdf)】
https://booth.pm/ja/items/4102300

冒頭5問をサンプルとして無料公開しています
https://qiita.com/sano192/items/6361ed72106cb6dd5843

『AtCoder　凡人が『緑』になるための精選50問詳細解説』

AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段：100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/

【booth(pdf)】
https://sano192.booth.pm/items/3179185

1～24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf

『AtCoder ABC201～225 ARC119～128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV

【booth(pdf)】
https://booth.pm/ja/items/3698647

ARC119~128の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/

【booth(pdf)】
https://sano192.booth.pm/items/3698668

『AtCoder ABC226～250 ARC129～139 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』

ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif：0～1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。

サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733

Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える？】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。

値段：300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS

【booth(pdf)】
https://sano192.booth.pm/items/4025713

ARC129～139の部分のみ抜粋した廉価版 もあります。
値段：200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF

【booth(pdf)】
https://sano192.booth.pm/items/4025737

『Excelでリバーシを作ろう!!　マクロ、VBAを1から学ぶ』

Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です！
マクロ、VBAが全くわからない人でも大丈夫！　丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます！
値段：300円(Kindle Unlimited対象)

サンプルとして「準備」～「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb

【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW

【booth(pdf】
https://sano192.booth.pm/items/3785312