ウルシステムズプログラミングコンテスト2023(AtCoder Beginner Contest 286) A~E問題の解説記事です。
灰色~茶色コーダーの方向けに解説しています。
その他のABC解説、動画などは以下です。
更新時はツイッターにて通知します。
https://twitter.com/AtCoder4
ウルシステムズ株式会社様について
【新卒採用】
https://ulsystems-recruit.snar.jp/jobboard/apply.aspx
【中途採用】
https://hrmos.co/pages/ulsystems/jobs
A Dif:30
A問題にしては少し難しい問題だったと思います。
まずAの要素をリストで受け取り、1~P-1,P~Q,Q+1~R-1,R~S,S+1~Nの5箇所へ分けましょう。
入力例4であれば
10 2 4 7 9
22 75 26 45 72 81 47 29 97 2
1~P-1(=1~1):22
P~Q(=2~4):75 26 45
Q+1~R-1(=5~6):72 81
R~S(=7~9):47 29 97
S+1~N(=9~10):2
となります。
Bを出力するときは
「1~(P-1)」+「R~S」+「(Q+1)~(R-1)」+「P~Q」+「(S+1)~N」
とつなげればOKです。
リストのA番目からB番目を取り出すときは
リスト[A:B+1]
と書きます。リスト[A:B]としないように注意してください。
pythonはリストの先頭を0番目と数えるため、問題文のA1がA[0],A2がA[1],...と一つずつずれてしまいます。
こういうときはリストを受け取るときに先頭に[0]などてきとうな数を埋めておくと、A1=A[1],A2=A[2],....というようにできて楽です。
入力の受け取り、出力がわからない方は以下の記事を参考にしてください。
【提出】
# 入力の受け取り
N,P,Q,R,S=map(int, input().split())
# 最初に[0]を埋めて番号をずらす
A=[0]+list(map(int, input().split()))
# 1~P-1
A1=A[1:P]
# P~Q
A2=A[P:Q+1]
# Q+1~R-1
A3=A[Q+1:R]
# R~S
A4=A[R:S+1]
# S+1~N
A5=A[S+1:N+1]
# つなげる
B=A1+A4+A3+A2+A5
# 出力(「*」をつけるとかっこなしで出力できる)
print(*B)
B Dif:32
pythonでは
文字列.replace(変換前の文字,変換後の文字)
として文字を変換できます。これを使えば簡単です。
【提出】
# 入力の受け取り
N=int(input())
S=input()
# "na"→"nya"へ変換
S=S.replace("na","nya")
# 出力
print(S)
C Dif:565
C問題なので全探索(全パターンを試す)ができないかなと考えてみましょう。
B円の操作しかなければS[0]とS[N-1],S[1]とS[N-2],...,S[i]とS[N-i-1]が同じでなけばB円払って、片方をもう片方へ合わせるということを繰り返すことで回文を作れます。
これをi=0,1,2,...,(N//2-1)について確認し、合計金額を確認すればOKです。
これを
A円の操作をしない場合
A円の操作を1回した場合
A円の操作を2回した場合
...
A円の操作を(N-1)回した場合
それぞれについて確認し、金額が最も小さいものを探します。
先頭の文字を消す、という操作は普通に文字列のままでやるとO(N)かかるので、dequeを使って処理します。
dequeについて
dequeはリストのようなものですが、先頭から要素を取り出す操作をO(1)で行うことができます。
(リストだとO(N)かかります)
インポート:from collections import deque
作成:変数名=deque()
先頭(左端)に要素追加【O(1)】:変数名.appendleft(要素)
末尾(右端)に要素追加【O(1)】:変数名.append(要素)
先頭(左端)から要素を取り出して削除【O(1)】:変数名.popleft()
末尾(右端)から要素を取り出して削除【O(1)】:変数名.pop()
【使用例】
# インポート:from collections import deque
from collections import deque
# 作成:変数名=deque()
que=deque()
# 先頭(左端)に要素追加【O(1)】:変数名.appendleft(要素)
que.appendleft(1)
# 末尾(右端)に要素追加【O(1)】:変数名.append(要素)
que.append(3)
# 先頭(左端)から要素を取り出して削除【O(1)】:変数名.popleft()
x=que.popleft()
# 末尾(右端)から要素を取り出して削除【O(1)】:変数名.pop()
y=que.pop
詳しく知りたい人は以下のページを見てください。
pythonでは間に合わないのでpypyで提出します。
【提出】
# pypyで提出
# 入力の受け取り
N,A,B=map(int, input().split())
S=input()
# dequeのインポート
from collections import deque
# Sを1文字ずつリストへ展開
S=list(S)
# dequeへ入れる
S=deque(S)
# 答え(初期値は大きい数)
ans=10**15
# Ac=0~(N-1):操作Aの回数
for Ac in range(N):
# 操作Bの回数
Bc=0
# k=0~(N//2-1)
for k in range(N//2):
# S[k]とS[N-1-k]が違う場合
if S[k]!=S[N-1-k]:
# 操作Bを行う
Bc+=1
# 合計金額が安ければ更新
ans=min(A*Ac+B*Bc,ans)
# 操作Aを行う
# Sの先頭の要素を取り出し
Sf=S.popleft()
# 先頭の要素を末尾へ
S.append(Sf)
# 答えの出力
print(ans)
D Dif:607
全パターン試してみましょう。
例えば入力が
2 30
10 2
5 3
だった場合、
まず10円が2枚あるので10,20円が作れます。全く使わない場合もあるので0円も作れます。
これらをセットに記録します。セットの名前はMoneyとしておきましょう。
Money=(0,10,20)
次に5円が3枚です。0,5,10,15円が作れます。
0円に0円足して0円
0円に5円足して5円
0円に10円足して10円
0円に15円足して15円
10円に0円足して10円(重複なのでセットには記録されません)
10円に5円足して15円(重複なのでセットには記録されません)
10円に10円足して20円
10円に15円足して25円
20円に0円足して20円(重複なのでセットには記録されません)
20円に5円足して25円(重複なのでセットには記録されません)
20円に10円足して30円
20円に15円足して35円
最後の35円はX=30より大きいので記録する意味がないです。
よってMoney=(0,5,10,15,20,25,30)となります。
Moneyの中にX=30があるので答えはYesです。
実装では以下の手順で行います。
(1)Moneyに0を追加する。
(2)入力を受け取る。
(3)tmpMoneyというリストを用意する。これはMoneyの要素に作れる金額を足した結果を格納するセット。
(4)Moneyの各要素へ作れる金額を足す。ただし合計がXを超えたら無視。
(5)MoneyをtmpMoneyへ置き換える
最後にXがMoneyの中にあれば「Yes」となります。
pythonでは間に合わないのでpypyで提出します。
【提出】
# pypyで提出
# 入力の受け取り
N,X=map(int, input().split())
# セットを用意
Money=set()
# 0を追加
Money.add(0)
# N回
for i in range(N):
# 入力の受け取り
A,B=map(int, input().split())
# Moneyの要素に作れる金額を足した結果を格納するセット
tmpMoney=set()
# m:Moneyの各要素
for m in Money:
# i=0~B
for i in range(B+1):
# A円をi枚使う、合計の金額がX以下なら
if m+A*i<=X:
# 追加
tmpMoney.add(m+A*i)
# 更新
Money=tmpMoney
# XがMoneyの中にあれば
if X in Money:
# 「Yes」を出力
print("Yes")
# そうでなければ
else:
# 「No」を出力
print("No")
E Dif:1128
ちょっとややこしい最短経路問題ですね。
最短経路といえば「ダイクストラ法」か「ワーシャルフロイド法」だ!とならなければこの問題は解けません。
今回はワーシャルフロイド法を使います。
ワーシャルフロイド法は「経由していい頂点を1個ずつ増やしながら各頂点間の最短経路を探す」というようなアルゴリズムです。
例を見てみましょう。
入力例1で考えます。
5
30 50 70 20 60
NYYNN
NNYNN
NNNYY
YNNNN
YNNNN
まず各都市間に直行便があるかを表で示します。直行便がある場合は距離=直行便の本数を1、そうでなければ∞としておきます。
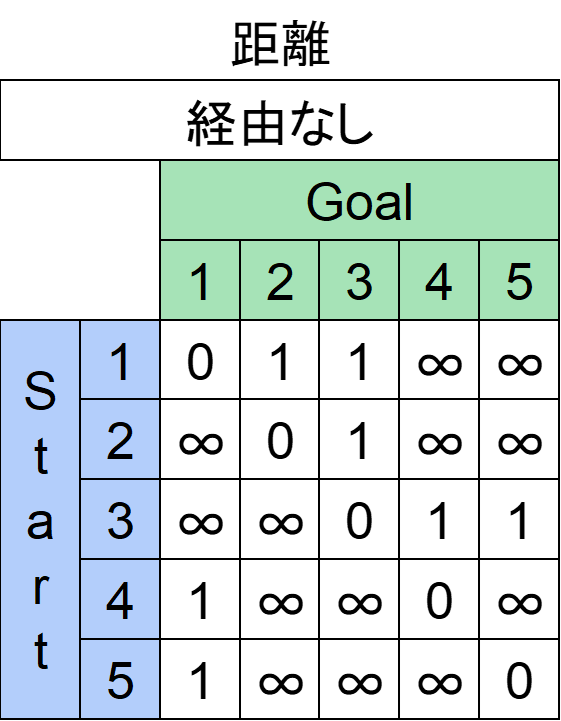
これがどこの都市も経由してはいけない場合の最短経路です。
ついでに買えるお土産の情報も表にまとめておきます。この表にはStartからGoalへ進んだとき、Goalの地点で買えるお土産の価値だけ書きます。
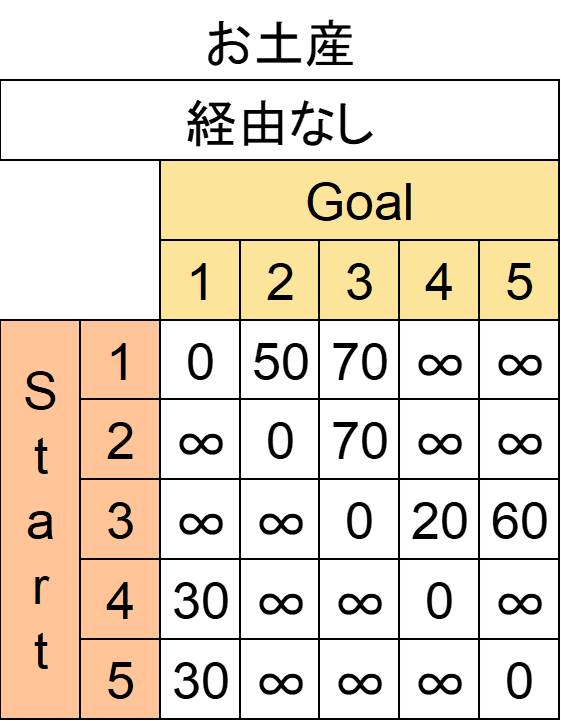
ではまず1つ目、「都市1までを経由してよい場合」を考えましょう。
結論から言うと以下のようになります。
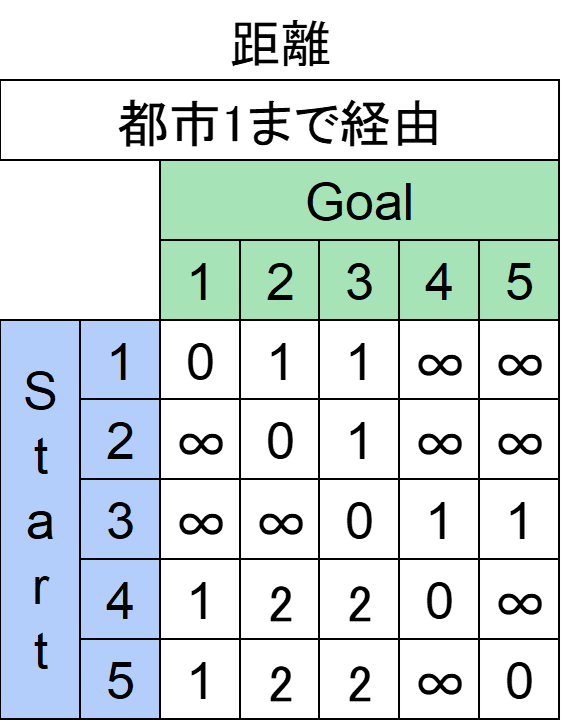
いくつか「2」が増えました。
例えば都市4→都市2へ行く場合、直行便はありませんが、都市4→都市1→都市2と進むことができます。そのため直行便の本数=2が埋まりました。
ではお土産の価値はどうなるでしょうか。
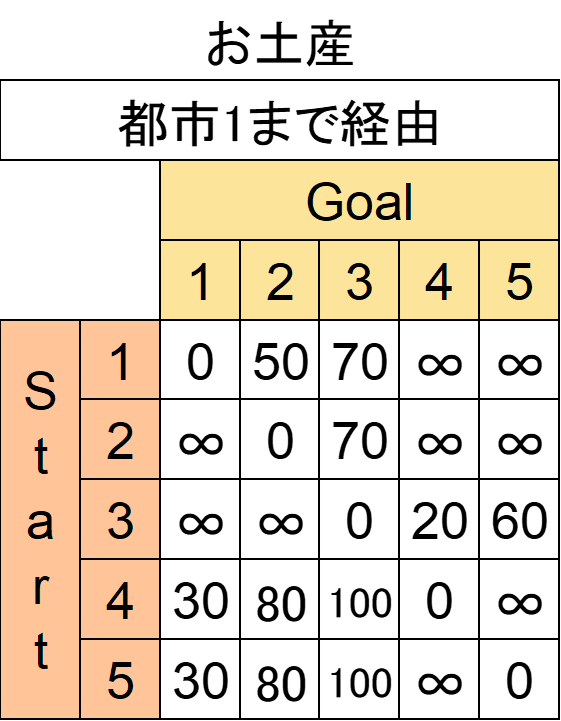
都市4→都市1→都市2と進む場合、この場合も出発点である都市4のお土産は無視して、都市1,都市2のお土産だけ記載します。
都市1は価値30、都市2は価値50なので合計80になるわけです。
他の経路も同様に計算しています。
次に「都市2までを経由してよい場合」を考えます。重要なのは「都市2を経由してよい」ではなく「都市2までを経由してよい」ということです。
つまり都市1も経由してよいということです。
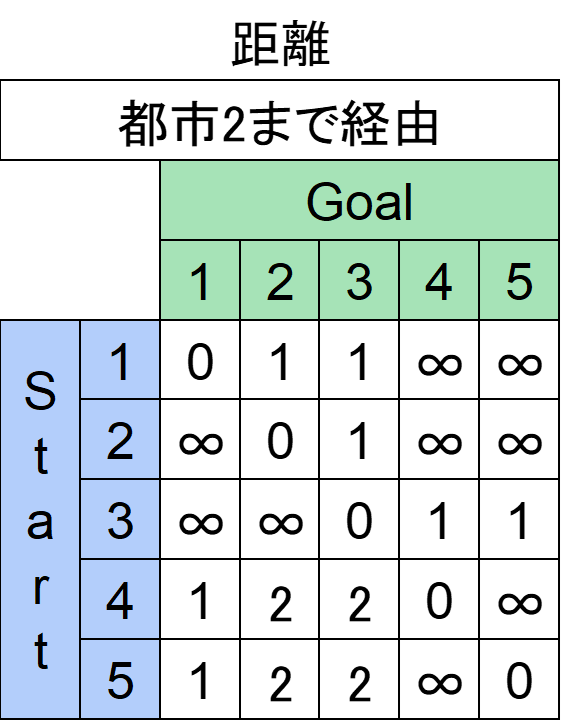
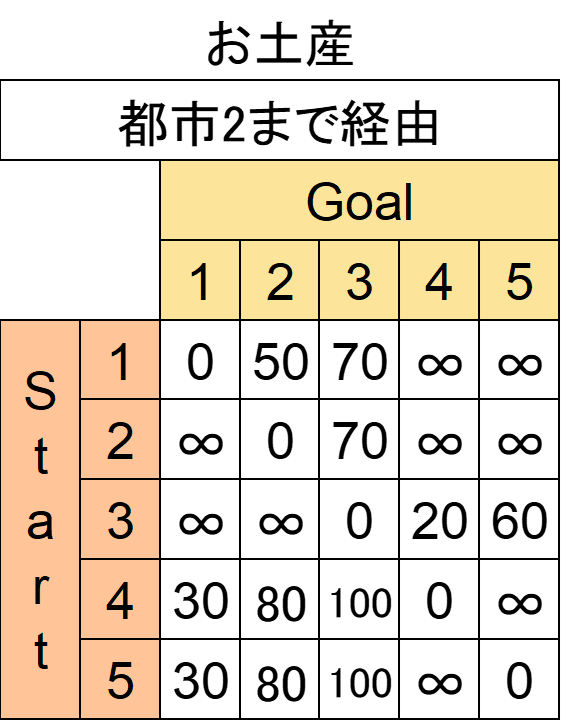
何も変わっていませんね。
都市2が経由できる場合、例えば都市5から都市3へ行くために都市5→都市1→都市2→都市3というルートが考えられます。
しかし都市1が経由できる場合の時点で都市5から都市3は直行便の本数2が埋まっていました。ですのでわざわざ直行便本数を増やす上記のルートで3に更新する意味がありません。
つまり更新するのは経由することで距離がより小さくなる場合のみです。距離の表をd[S=スタート地点][G=ゴール地点]として、もし都市kを経由した方が小さければ更新とするので、
・d[S][k]+d[k][G]<d[S][G]の場合:d[S][G]=d[S][k]+d[k][G]
となります。この時お土産も都市k、都市Gで買うとして(都市Sは無視して)、お土産の表をvとした時v[S][G]=v[S][k]+v[k][G]と更新します。
では距離=直行便本数が同じルート、すなわちd[S][k]+d[k][G]=d[S][G]の場合はどうでしょうか。
この場合はお土産の価値で判断します。すなわちv[S][G]<v[S][k]+v[k][G]であればそれまでに記録したルートより合計価値の高いお土産が買えるので更新します。
これらをまとめます。
・d[S][k]+d[k][G]<d[S][G]の場合(都市kを経由した方が直行便本数が少ない)
d[S][G]=d[S][k]+d[k][G]
v[S][G]=v[S][k]+v[k][G]
・d[S][k]+d[k][G]=d[S][G] かつ v[S][G]<v[S][k]+v[k][G](都市kを経由した方がより合計価値の高いお土産が買える)
v[S][G]=v[S][k]+v[k][G]
これらの式を使ってk=1,2,3,...,Nについて、表を更新していきます。
k=Nまで処理を行えば「都市Nまでを経由してよい場合」すなわち全ての都市を経由してよい場合について最短の直行便本数と、お土産の価値が得られているので後はそれを出力すればOKです。
ただし、お土産の価値についてはスタート地点で買えるお土産の価値を出力前に足すことを忘れないようにしましょう。
pythonでは間に合わないのでpypyで提出します。
【提出】
# pypyで提出
# 入力の受け取り
N=int(input())
# 0番目を[0]で埋めて番号を1インデックスにする
A=[0]+list(map(int, input().split()))
# 到達不能距離(大きければ何でもOK)
inf=10**10
# 距離=直行便本数の表
d=[[inf]*(N+1) for i in range(N+1)]
# お土産の価値
v=[[0]*(N+1) for i in range(N+1)]
# i=1~N
for i in range(1,N+1):
# 入力の受け取り(0文字目を埋めて1インデックスに)
Stmp="0"+input()
# j=1~N
for j in range(1,N+1):
# Sのj文字目が「Y」ならば
if Stmp[j]=="Y":
# 都市i→都市jの直行便が存在
d[i][j]=1
# 都市jで買えるお土産の価値を記録
v[i][j]=A[j]
# ここはなくてもOK
# i=1~N
for i in range(1,N+1):
# i=1~N
for i in range(1,N+1):
# 都市i→都市iの距離を0に
d[i][i]=0
# k=1~N
for k in range(1,N+1):
# S=1~N
for S in range(1,N+1):
# G=1~N
for G in range(1,N+1):
# 都市kを経由した方が距離が短い⇔直行便本数が少ない
if d[S][k]+d[k][G]<d[S][G]:
# 更新
d[S][G]=d[S][k]+d[k][G]
v[S][G]=v[S][k]+v[k][G]
# 距離が同じ かつ 都市kを経由した方がお土産の合計価値が高い
elif d[S][k]+d[k][G]==d[S][G] and v[S][G]<v[S][k]+v[k][G]:
# 更新
v[S][G]=v[S][k]+v[k][G]
# 入力の受け取り
Q=int(input())
# Q回
for i in range(Q):
# 入力の受け取り
U,V=map(int, input().split())
# 都市U→都市Vが到達不能
if d[U][V]==inf:
# 「Impossible」を出力
print("Impossible")
# 都市U→都市Vが到達可能
else:
# 距離と合計価値を出力
# 合計価値は出発地点の分を足す
print(d[U][V],A[U]+v[U][V])
【広告】
『AtCoder 最速で緑になる 基礎・典型50問詳細解説』
ABC201~250から基礎・典型問題50問をとてつもなく丁寧かつ詳細に解説した本(kindle)、pdf(booth)です。
灰色、茶色コーダーにおすすめ!
値段:100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BBB7RKTP
【booth(pdf)】
https://booth.pm/ja/items/4102300
冒頭5問をサンプルとして無料公開しています
https://qiita.com/sano192/items/6361ed72106cb6dd5843
『AtCoder 凡人が『緑』になるための精選50問詳細解説』
AtCoderで緑になるための典型50問をひくほど丁寧に解説した本(kindle)、pdf(booth)を販売しています。
値段:100円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/gp/product/B09C3TPQYV/
【booth(pdf)】
https://sano192.booth.pm/items/3179185
1~24問目まではサンプルとして無料公開しています
https://qiita.com/sano192/items/eb2c9cbee6ec4dc79aaf
『AtCoder ABC201~225 ARC119~128 灰・茶・緑問題 超詳細解説 AtCoder 詳細解説』
ABC201~225、ARC119~128 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを5問分公開しています
https://qiita.com/sano192/items/3258c39988187759f756
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC119~128の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVK3SLV
【booth(pdf)】
https://booth.pm/ja/items/3698647
ARC119~128の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B09TVKGH17/
【booth(pdf)】
https://sano192.booth.pm/items/3698668
『AtCoder ABC226~250 ARC129~139 灰・茶・緑問題 超詳細解説』
ABC226~250、ARC129~139 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを4問分公開しています
https://qiita.com/sano192/items/f8f09ea769f2414a5733
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC129~139の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G13QMS
【booth(pdf)】
https://sano192.booth.pm/items/4025713
ARC129~139の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0B7G337YF
【booth(pdf)】
https://sano192.booth.pm/items/4025737
『AtCoder ABC251~275 ARC140~151 灰・茶・緑問題 超詳細解説』
ABC251~275、ARC140~151 の 灰・茶・緑DIfficulty問題(Dif:0~1199) を解説しています。
とにかく 細かく、丁寧に、具体例を豊富に、実装をわかりやすく、コードにコメントをたくさん入れて 解説しています。
サンプルを4問分公開しています
https://qiita.com/sano192/items/810a4a7d5cf61321bb05
Qiitaにて無料公開している『ものすごく丁寧でわかりやすい解説』シリーズをベースにしていますが、 【キーワード】【どう考える?】【別解】を追加 し、 【解説】と【実装のコツ】を分ける ことでよりわかりやすく、 具体例や図もより豊富に 書き直しました。
Qiitaには公開していない ARC140~151の灰・茶・緑DIfficulty問題も書き下ろし ています。
値段:300円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BRNTM9Z4
【booth(pdf)】
https://sano192.booth.pm/items/4455120
ARC140~151の部分のみ抜粋した廉価版 もあります。
値段:200円(Kindle Unlimited対象)
【kindle】
https://www.amazon.co.jp/dp/B0BRNRXPCV
【booth(pdf)】
https://sano192.booth.pm/items/4455133
『Excelでリバーシを作ろう!! マクロ、VBAを1から学ぶ』
Excelのマクロ(VBA)で「三目並べ」「マインスイーパー」「リバーシ」を作る解説本です!
マクロ、VBAが全くわからない人でも大丈夫! 丁寧な解説と図でしっかり理解しながら楽しくプログラミングを学ぶ事ができます!
値段:300円(Kindle Unlimited対象)
サンプルとして「準備」~「三目並べ」を無料公開しています。
https://qiita.com/sano192/items/9a47e6d73373d01e31fb
【kindle】
https://www.amazon.co.jp/dp/B09XLM42MW
【booth(pdf】
https://sano192.booth.pm/items/3785312