PyTorchチュートリアルをみていたら、機械学習のウォーミングアップとしてとてもシンプルなプログラムの紹介があったので、少し手を動かして追ってみました。これは Numpy だけを使った機械学習のエッセンスです。Pytorch も使っていません。 自分用の備忘録であるとともに、これから機械学習を勉強しようという方のためにも少しは役立つかもしれません。
PyTorchチュートリアル/1. PyTorch基礎/[5] 例題を用いた、PyTorchの各要素の解説
【関連記事】
MNIST手書き数字のCNN画像認識 - Qiita
CNN 畳み込み層のメモ - Qiita
Softmax+CrossEntropy の実装 - Qiita
機械学習のウォーミングアップ(Numpy) - Qiita
1. 線形ノードの誤差逆伝播法
このプログラムで使われている各ノードについて予め見ておきたいと思います。
線形ノードでの誤差逆伝播法の詳細が知りたいときは、以下の過去記事を参照してください。
【機械学習】誤差逆伝播法のコンパクトな説明 - Qiita
機械学習ネットワークの線形関数ノード(MatMul,行列積)の誤差逆伝播法
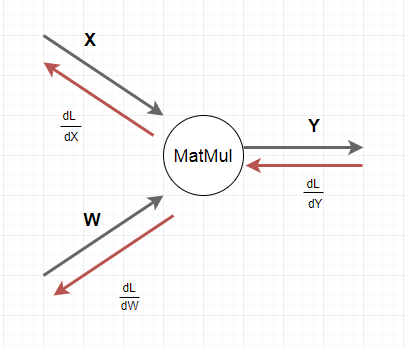
- X: 入力ベクトル
- Y: 出力ベクトル
- W: 行列パラメータ、 Y = X・W
この時、損失計算L の 行列パラメータW による微分 $\frac{\partial L}{\partial W}$ と、入力ベクトルX による微分 $\frac{\partial L}{\partial X} $ は以下のように求められます。ここで $\frac{\partial L}{\partial Y}$ は逆向きに線形ノードに入ってくる 損失計算L の出力ベクトルY による微分になります。
\begin{align}
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\\
&[1]\quad \frac{\partial L}{\partial W} = X^T \times \frac{\partial L}{\partial Y}\\
\\
&[2]\quad \frac{\partial L}{\partial X} = \frac{\partial L}{\partial Y} \times W^T
\\
\end{align}
同様にReLU 関数ノードの誤差逆伝播法は以下のようになります。
ReLU 関数ノードの誤差逆伝播法
- X: 入力ベクトル
- Y: 出力ベクトル
\begin{align}
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\\
\quad Y = &\left\{
\begin{array}{ll}
X & (X \geq 0) \\
0 & (X \lt 0)
\end{array}
\right.
\\
\\
[3]\quad \frac{\partial Y}{\partial X} = &\left\{
\begin{array}{ll}
1 & (X \geq 0) \\
0 & (X \lt 0)
\end{array}
\right.
\\
\end{align}
損失関数の誤差逆伝播法
Y: 入力ベクトル
T: 正解データ
\begin{align}
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\\
& loss(Y,T) = \sum_i (Y_i - T)^2\\
\\
& Yベクトルの成分Y_iごとに微分すると、他の成分Y_jは定数と考えられるので、\\
& \frac{\partial loss(Y,T)}{\partial Y_i} = 2(Y_i-T)\\
\\
&つまりまとめて書くと、\\
&[4]\quad \frac{\partial loss(Y,T)}{\partial Y} = 2(Y-T)
\\
\end{align}
2. ウォーミングアップ
ここでは PyTorchチュートリアル にウォーミングアップとして紹介してある、Numpy による機械学習の骨格の実装を紹介したいと思います。とてもシンプルな実装なので、上で紹介した 誤差逆伝播法 の知識さえ理解していれば、簡単に理解できるでしょう。
PyTorchチュートリアル/1. PyTorch基礎/[5] 例題を用いた、PyTorchの各要素の解説
2-1. 計算グラフもどき
まずは、ここで使われる機械学習ネットワークの計算グラフもどきを示しておきたいと思います。L1 と L2 は線形ノードです。誤差逆伝播法では、ここに上の式[1][2][3][4]が適用されます。損失関数で言えば、lossの入力ベクトルは Y=y_pred で、 正解データが T = y であることに注意してください。
x h = x.dot(w1) h_relu = np.maximum(h, 0) y_pred = h_relu.dot(w2) np.square(y_pred - y).sum()
--- L1 ------------- relu --------------------------- L2 ------------------------- loss ---------------------------
| grad_h grad_h_relu | grad_y_pred = 2.0 * (y_pred - y) [4]
| = grad_h_relu[3] = grad_y_pred.dot(w2.T) [2] |
| grad_w1 = x.T.dot(grad_h) [1] | grad_w2 = h_relu.T.dot(grad_y_pred) [1]
w1 w2
2-2. ウォーミングアップ:Numpy
このような小さなプログラムで、誤差逆伝播法を含めた、機械学習のフレームワークを表現できていることに驚きです。入力データが全く意味を持たないダミーなので、逆に仕組みの部分だけがクローズアップされる感じです。
# -*- coding: utf-8 -*-
import numpy as np
# N:バッチサイズ D_in:入力層の次元数
# H:隠れ層の次元数 D_out: 出力層の次元数
N, D_in, H, D_out = 64, 1000, 100, 10
# 乱数により入力データと目標となる出力データを生成
x = np.random.randn(N, D_in)
y = np.random.randn(N, D_out)
# 乱数による重みの初期化
w1 = np.random.randn(D_in, H)
w2 = np.random.randn(H, D_out)
learning_rate = 1e-6
for t in range(500):
# 順伝播: 予測値yの計算
h = x.dot(w1)
h_relu = np.maximum(h, 0)
y_pred = h_relu.dot(w2)
# 損失の計算と表示
loss = np.square(y_pred - y).sum()
if t % 100 == 99:
print(t, loss)
# 逆伝搬:損失に対するW1とw2の勾配の計算
grad_y_pred = 2.0 * (y_pred - y)
grad_w2 = h_relu.T.dot(grad_y_pred)
grad_h_relu = grad_y_pred.dot(w2.T)
grad_h = grad_h_relu.copy()
grad_h[h < 0] = 0
grad_w1 = x.T.dot(grad_h)
# 重みの更新
w1 -= learning_rate * grad_w1
w2 -= learning_rate * grad_w2
実行結果は以下の通りになります。損失値がゼロに近づいていく様がわかります。
99 698.9261552653923
199 5.4262507825288235
299 0.07003111577934468
399 0.0010654694386880146
499 1.7590186185590355e-05
今回は以上です。