統計学入門のお供 Julia (1) - 標準得点、偏差値得点 - Qiita
統計学入門のお供 Julia (2) - ピアソンの積率相関係数 - Qiita
統計学入門のお供 Julia (3) - 順位相関係数と自己相関係数 - Qiita
統計学入門のお供 Julia (4) - 最小二乗法と決定係数 - Qiita
統計学入門のお供 Julia (5) - ベイズの定理 - Qiita
統計学入門のお供 Julia (6) - ド・メレの問題 = Oiita
統計学を勉強するため「統計学入門」(東京大学出版会)を読み始めました。練習問題があるのですが、これも勉強中のJuliaを使って計算していきたいと思います。
「確率論入門」(ちくま学芸文庫、赤攝也)も参考にしています。確率論の基礎的なところの考え方を詳細に説明してあります。特に多重試行の説明は詳しいです。文庫本なので持ちやすく読みやすいです。
組み合わせの計算には、Julia言語のBaseのMathematicsカテゴリのbinomial関数を使います。BaseなのでMathematicsカテゴリの関数は特に何もしなくとも利用できます。
Mathematics
https://docs.julialang.org/en/v1/base/math/
1.ド・メレの問題
P85 問4.1
問 i)
サイコロを4回投げるとき、6の目が少なくとも1回出るのに賭けるか、1回も出ない方に賭けるか?
3通りの方法で解いてみます。
\begin{align}
&サイコロを振りどの目が出るかを確認する試行を考える。\\
&\Omega : 全事象 \\
&E_i \quad (i=1,2,3,4): \Omega の部分集合とするとき以下のように定義する。\\
&(E_1, E_2, E_3, E_4) \equiv \{ (a_1, a_2, a_3, a_4) | a_i \in E_i \quad
i=1,2,3,4\}\\
&これは4回続けてサイコロを振る事象を表している。\\
\\
&今サイコロを振った時に、6が出る事象をEとする。\\
\\
&4回続けてサイコロを振った時に少なくとも1回は6が出る事象は、\\
&4回連続して6以外が出る事象の補集合と考えられる。\\
&また4回連続して6以外が出る事象は以下のように表現できる。\\
&F^{(4)} \equiv (E^c, E^c, E^c, E^c)\\
\\
&故に\\
&P(F^{(4)}) = P(E^c) P(E^c) P(E^c) P(E^c) = P(E^c)^4=(5/6)^4\\
\\
&求める確率は 1-(5/6)^4 = 0.5177469135802468\\
\\
\\
\\
&************************************\\
\\
&別解です。\\
&補集合で考えるのではなく、もう少し正面から解いてみます。\\
\\
&4回続けてサイコロを振った時に、少なくとも1回は6が出る事象は以下のように表現される。\\
&E^{(4)} \equiv (E, \Omega, \Omega, \Omega) \cup (\Omega, E, \Omega, \Omega) \cup (\Omega, \Omega, E, \Omega) \cup (\Omega, \Omega, \Omega, E) \tag{1}\\
\\
\\
&加法の定理 : P(A \cup B) =P(A) + P(B) - P(A \cap B) \tag{2}\\
\\
&加法の定理を繰り返し使うことで、以下が導かれる\\
&P(A \cup B \cup C \cup D) = P(A) + P(B) + P(C) +P(D)\\
&\quad
- P(A \cap B) - P(A \cap C) - P(A \cap D) - P(B \cap C) - P(B \cap D) - P(C \cap D)\\
&\quad + P(A \cap B \cap C) + P(A \cap B \cap D) + P(A \cap C \cap D) + P(B \cap C \cap D)\\
&\quad - P(A \cap B \cap C \cap D) \tag{3}\\
\\
&A=(E, \Omega, \Omega, \Omega), \quad B= (\Omega, E, \Omega, \Omega), \\
&C=(\Omega, \Omega, E, \Omega),\quad D=(\Omega, \Omega, \Omega, E)として(3)を置き換える。\\
\\
\\
&P(E^{(4)}) =P(E, \Omega, \Omega, \Omega)+P(\Omega, E, \Omega, \Omega)+P(\Omega, \Omega, E, \Omega)+P(\Omega, \Omega, \Omega, E)\\
&-P(E, E, \Omega, \Omega)-P(E, \Omega, E, \Omega)-P(E, \Omega, \Omega, E)-P(\Omega, E, E, \Omega)\\
&-P(\Omega, E, \Omega, E)-P(\Omega, \Omega, E, E)\\
&+P(E, E, E, \Omega)+P(E, E, \Omega, E)+P(E, \Omega, E, E)+P(\Omega, E, E, E)\\
& - P(E, E, E, E)\\
&=4*(1/6) -6*(1/6)^2+4*(1/6)^3-(1/6)^4=0.5177469135802469
\\
\\
&誤差を除いて、計算結果は同じです。\\
&最初の方が簡単だけど、別解の方が全体の構造が良くわかり汎用性があります。\\
\\
\\
&************************************\\
\\
&別解2です。\\
&2項分布の考え方で解いてみます。\\
\\
&確率変数 X_i^{(4)} を以下のように定義する。\\
\\
&X_i^{(4)}(a_1,a_2,a_3,a_4) = 1 \qquad (a_i \in E)\\
&X_i^{(4)}(a_1,a_2,a_3,a_4) = 0 \qquad (a_i \notin E)\\
\\
&この時、確率変数S^{(4)}を以下のように定義する。\\
\\
&S^{(4)} \equiv X_1^{(4)} + X_2^{(4)} + X_3^{(4)} + X_4^{(4)}\\
\\
&S^{(4)}(a_1,a_2,a_3,a_4) = k は、\\
&a_1,a_2,a_3,a_4 のうちEに属するものの個数がk個であることを意味します。\\
&当然、0 \leqq k \leqq 4 が成り立ちます。\\
\\
&\{ S^{(4)}=k \} \equiv \{(a_1,a_2,a_3,a_4) \in (\Omega,\Omega,\Omega,\Omega) \quad | \quad S^{(4)}
(a_1,a_2,a_3,a_4)=k \}
\\
\\
&例えばk=3の時は、以下のように4個から3個を選び出す組み合わ数\begin{pmatrix} 4 \\3 \end{pmatrix} 通りの\\
&お互いに背反な事象に分割されます。\\
\\
&\{ S^{(4)}=3 \} = (E,E,E,E^c) \cup (E,E,E^c,E) \cup (E,E^c,E,E) \cup (E^c,E,E,E)
\\
\\
\\
&一般に\{ S^{(4)}=k \}は、4個からk個を選び出す組み合わ数\begin{pmatrix} 4 \\k \end{pmatrix} 通りの\\
&お互いに背反な事象に分割されます。\\
&それぞれの事象の確率は、k個のEと、(4-k)個のE^cですからP(E)^k(1-P(E)^{(4-k)}です。\\
&P(\{ S^{(4)}=k \}) = \begin{pmatrix} 4 \\k \end{pmatrix} P(E)^k(1-P(E))^{(4-k)}\\
\\
\\
&各 \{ S^{(4)}=k \} \quad i=1,2,3,4は明らかに排反だから、求めるものは以下のようになる。\\
&P(\{ S^{(4)}=1 \})+P(\{ S^{(4)}=2 \})+P(\{ S^{(4)}=3 \})+P(\{ S^{(4)}=4 \})\\
\\
&後はJuliaのプログラムで解いてみたいと思います。
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\\
\end{align}
以下のプログラムはより汎用になっていますが、n=4、k=1で実行すれば問題と同じものです。
function mybinomial(k, n, p)
s = 0.0
for i in k:n
s += binomial(n,i)*(p)^i*(1-p)^(n-i)
end
s
end
mybinomial(1,4,1/6)
0.5177469135802469
2項分布で解いても同じ結果ですね。
問 ii)
サイコロを2回同時に24回投げるとき、(6,6)の目が少なくとも1回出るのに賭けるか、1回も出ない方に賭けるか?
(6,6)の目以外が24回連続して出る確率は以下の計算で求まる。
(35/36)^24
0.5085961238690966
2項分布でも求まる
(6,6)の目が少なくとも1回出る確率
mybinomial(1,24,1/36)
0.49140387613090303
(6,6)の目以外が24回連続して出る確率
1-mybinomial(1,24,1/36)
0.508596123869097
2.ホイヘンスの問題
P85 問4.2
2個のサイコロを何回投げれば、そのうちの1回は目の和が12の成る確率が0.9を越えるか?
本書の解答とは別会です。2項分布を使って以下のように確かめられます。
mybinomial(1,big(81),1/36)
8.97903928782527159074445136...e-01
mybinomial(1,big(82),1/36)
9.00739930760790253942017745...e-01
つまり82回投げればよい。
bigを使わないとOverflowErrorになります。big様ですね。
3.看護婦の問題
P85 問4.3
30人の看護婦を15人ずつの2組の交代勤務に分ける分け方は何通りか?
組み合わせの問題ですね。
binomial(30,15)
155117520
4.誕生日の問題
P85 問4.4
r人の集団中に同じ誕生日の人が少なくとも2人いる確率を考える問題です。
どうもしっくりこないので.....少し問題の文章を自分なりに噛み砕いてあります。確率における試行の意味を明確にしたかっただけですので、本質は変わりません。
\begin{align}
\\
&r人の集団を考える。\\
&壺の中に365個の玉があり、それぞれ1,2,3,..,365の番号が振られている。\\
\\
&神様はr人の誕生日を以下のrステップの手順で決める。\\
&(1)神様が壺から1個取り出し、1人目の誕生日を決める。印をつけて玉は戻す。\\
&(2)神様が壺から1個取り出し、2人目の誕生日を決める。印をつけて玉は戻す。\\
&.....\\
&(r)神様が壺から1個取り出し、r人目の誕生日を決める。印をつけて玉は戻す。\\
\\
&同じ誕生日の人が一組もいないことは、\\
&壺の中に、2つ以上の印ついているボールが存在しないことと同じ意味です。(*)\\
&そのような確率を、各ステップにおいて求めてみましょう。\\
\\
&(1)ステップにおいて印のついていない玉を選択する確率は1です。\\
&(2)ステップにおいて印のついていない玉を選択する確率は(365-1)/365です。\\
&(3)ステップにおいて印のついていない玉を選択する確率は(365-2)/365です。\\
&.....\\
&(r)ステップにおいて印のついていない玉を選択する確率は(365-r+1)/365です。\\
\\
&つまり2つ以上の印ついているボールが存在しない確率は以下の式になります。\\
\\
&P = ((365-1)/365)((365-2)/365).....((365-r+1)/365)
\\
&\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad\\
\end{align}
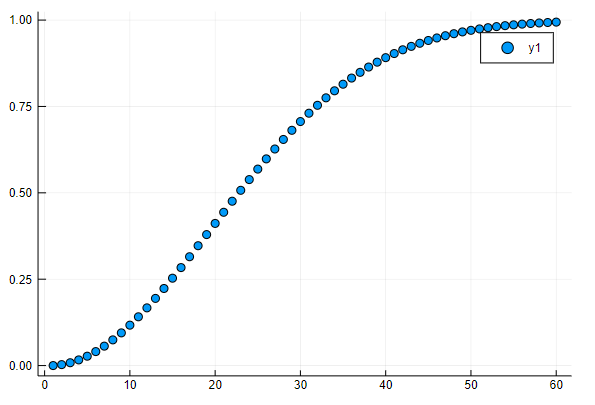
確率を求める式がわかったので、juliaでプログラムします。rをパラメータにして、1から60まで変化させ、それぞれの確率を計算します。最後にグラフとして描画します。
n=60
rs=zeros(n)
ps=zeros(n)
function mybirth(r)
p = 1.0
for i in 1:r
p *= ((365-i+1)/365)
end
1-p
end
function mybirth_r()
for r in 1:n
p = mybirth(r)
println("r=",r," p=",p)
rs[r] = r
ps[r] = p
end
1
end
mybirth_r()
using Plots
plot(rs,ps,seriestype=:scatter)
出力結果は以下の通りです。
r=1 p=0.0
r=2 p=0.002739726027397249
...
r=5 p=0.02713557369979347
...
r=10 p=0.11694817771107768
...
r=15 p=0.25290131976368646
...
r=20 p=0.41143838358058027
r=21 p=0.443688335165206
r=22 p=0.4756953076625503
r=23 p=0.5072972343239857
r=24 p=0.538344257914529
r=25 p=0.568699703969464
...
r=30 p=0.7063162427192688
...
r=35 p=0.8143832388747153
...
r=40 p=0.891231809817949
...
r=50 p=0.9703735795779884
...
r=60 p=0.994122660865348
60人いると、同じ誕生日ペアが、99%以上の確率で存在することになります。
rをx軸、確率をy軸にして描いたグラフは以下の通りです。
またこの問題は、以下のサイトで詳しく説明されています。
同じ誕生日の二人組がいる確率について - 高校数学の美しい物語
今回は以上です。