テレビゲームのRTAにおける最適チャート追求の部分的な理論化：「進め！キノピオ隊長」の場合

An English version (by Google Translate) is here.

お知らせ（本記事の執筆者によるRTAガイドの作成）

「進め！キノピオ隊長」Any% - Switch (Solo)のRTAガイドを作成しました。このゲームのRTA挑戦に興味がある方は、よかったらご覧ください。

本記事で得られた結果を手っ取り早く知りたい方は

計算結果をご覧ください。

改訂履歴

• 2023-01-03:
  • RTA in Japan Winter 2022出場結果を追記
• 2022-12-26:
  • 第1最適と第2最適（の1つ）の異なる部分について動画へのリンクを追記
• 2022-12-25:
  • プログラミングコードの いけてない部分 修正した部分について追記
• 2022-12-22:
  • RTA in Japan Winter 2022出場予定を追記
  • 参考を追記
• 2022-12-21:
  • 特定のステージのクリアにかかるタイムのサンプル値を追記
• 2022-12-19:
  • 取り得るチャートが何通りあるかの推定値を追記
• 2022-12-15:
  • 世界記録を更新したことを追記
• 2022-12-11:
  • ほかのRTAプレイヤーの記録で選択されているチャートを追記
• 2022-09-09:
  • 世界記録を樹立したことを追記
• 2022-05-15:
  • 解説図とその説明を追記
  • 計算結果の説明を追記
  • 発展の考察を追記
• 2022-05-02:
  • 解説図を追記
• 2022-04-06:
  • 計算結果を改訂
  • GitHubのリポジトリーを更新 (v1.2としてリリース)
• 2022-03-13:
  • 計算結果を改訂
  • GitHubのリポジトリーを更新 (v1.1としてリリース)
• 2022-01-15:
  • 入力データの例を追記
• 2022-01-14:
  • 計算結果を追記
  • 入力データに関する記載を追記
  • GitHubのリポジトリーを更新 (v1.0としてリリース)
• 2022-01-12 (初版)

ネタバレ注意

本記事は、「進め！キノピオ隊長」というテレビゲームソフトや、そのほかのスーパーマリオシリーズのゲームソフトのネタバレを含みます。それでもかまわない方のみ、読み続けてください。

RTA in Japan Winter 2022

(2022-12-22: 追記)
2022-12-26～2022-12-31の日程で開催される半年に一度の日本最大のRTAイベント「RTA in Japan Winter 2022」に「進め！キノピオ隊長」(Any% - Switch (Solo))で出場します！

予定

私の出番は27(火)午前です。最新のスケジュール表はこちらです。
スケジュールはイベントの進行状況によってリアルタイムに変わり、随時この表に反映されると聞いているので、イベントを視聴される方はこまめにチェックください。

結果

(2023-01-03: 追記)
楽しかったです。
タイムは1h20m02sで、この追記時点での自己ベスト（＝世界記録）から02m01sほど遅かったです。自己ベストとの差はあるものの、イベントでの一発勝負でこのタイムをだせる走者はなかなかいないと思うので、ある程度自分の力がだせて及第点の走りといったところでしょうか。なお、イベントの環境はふだんプレイしている環境とモニターのサイズや自分との距離が異なり、画面の細かいところを見たりジャイロのためにコントローラーを動かすのに影響が出たため、記録更新という高望みはしないでプレイしました。
クリアタイムが安定しているという理由で第2最適チャートを採用しましたが、第1最適チャートと唯一異なる3-26というステージで溶岩に落下して数十秒よけいにかかってしまいました。後述のとおり第2最適チャートで採用する3-26はクリアタイムが毎回ほぼ同じですが、ごくまれに今回のように失敗することがあり、その場合はステージの最初からやり直すことになるので数十秒よけいにかかります。これに対して第1最適チャートで採用する3-12は、クリアタイムは毎回変動して、場合によっては3-26の通常のクリアタイムより時間がかかってしまうことがあるものの、3-26で失敗した場合よりも遅くなることはまずありません。タイムが中くらいの範囲でブレる第1最適を選ぶか、ほとんどタイムは同じだがごくまれに大きく時間がかかってしまうリスクを持つ第2最適を選ぶか、悩ましくも興味深いトピックを残してくれた、RTA in Japanでの走りでした。

テレビゲームのRTAと数理最適化

テレビゲームの楽しみ方の一つに、何らかの設定された条件のもとでゲームソフト上の指定された地点や状態などから別の指定された地点や状態などに至るまでを人力操作によりできるだけ短時間で達成することを目指す「RTA」があります。例えば、「スーパーマリオブラザーズ」でゲームをスタートさせてからマリオやルイージを操作してできるだけ短時間でピーチ姫を救出する、などです。Speedrun.comに代表されるRTA記録集サイトには、日々、世界中から、多くのゲームソフトの高速プレイ録画リンクが提出され、録画動画の審査を経て、ランキング表が更新されています。RTAプレイヤーは、このランキング表の上位を目指して競っている、あるいは、自己ベストタイムを縮めることに挑戦をしています。

RTAにおいては、「チャート」と呼ばれる「短時間で目標を達成し得る操作の一連の流れ」を発見および改良することと、できるだけチャートどおりに操作を実践することの両面で、プレイヤーによる研究や鍛錬が進んでいます。前者については、コミュニティー内において、時折、チャートの（専門用語ではない通常の日本語のニュアンスとしての）最適化や、理論的に達成可能な最短タイム、といった言葉が登場します。ですが、理論的最短タイムを実現し得る真の最適チャートを探しだすことは、バグを含むゲームソフトのコードやそれが動くゲーム機の挙動の完全な把握が必要になることと、操作の選択が1秒間だけでも数十回（例えば、秒間60フレームのゲームソフトの場合、1秒間に60回）発生しそれがタイムぶん生じて膨大な総数になることから、たいへん困難です。そのため、チャートの発見・改良は、プレイヤーによる試行錯誤によるものがほとんどです。

さて、「何らかの与えられた条件のもとで目的とする評価値を最小あるいは最大にする解を求める」手法群である「数理最適化」が、チャートの発見・改良に役立てられないか？完全に理論的な最短タイムの導出は無理ではあるが、一部に仮定を置き、仮定していない部分について数理最適化を用いてチャートを導出することで、「もしその仮定が正しければこのチャートは理論的な最短タイムを実現し得る」という、条件付きの理論化ができないか？というのが、本記事の執筆動機になります。

ただし、ゲームソフトにはさまざまなジャンルやシステムのものがあり、一律に同一の数理最適化手法を適用することはできないので、本記事では特定の一つのソフトを対象にします。そして最後に、ほかのソフトへの応用可能性について言及します。

対象：「進め！キノピオ隊長」

本記事では、「進め！キノピオ隊長」というゲームソフトを対象にします。このゲームは「スーパーマリオ 3Dワールド」のスピンオフとして開発されたものです。Wii U版が2014年に、Nintendo Switch版とニンテンドー3DS版が2018年に発売されました。
ソフトのジャンルは、3Dパズルアクションです。独立した複数のステージが存在し、各ステージについて、主人公であるキノピオ隊長やキノピコ、ギミックなどを操作して動かし、用意されたゴール地点を目指すものです。

数理最適化の適用範囲

「進め！キノピオ隊長」のチャートのどの部分を数理最適化を用いて導出するかを明確にするため、以下、整理をします。

RTAのカテゴリー

RTAでは、通常、一つのゲームソフトに対して、達成目標が異なる複数の「カテゴリー」が設定されており、達成タイムのランキング表はカテゴリー別に掲載されています。本記事では、Speedrun.comで設定されているカテゴリーのうち、「Any% - Switch (Solo)」を対象とします。これは、Nintendo Switch版を1人でプレイするという前提で、プレイヤーの操作キャラであるキノピオ隊長を動かし始めてから3-28のゴール地点というところに到達するまでの時間を計測するカテゴリーです。その道中に関しては特に何もルールはありません。

ゲームソフトの進行構成

ゲームソフトが進行していく様子の特徴をまとめます。番号付き箇条書き部分は抽象的に、番号なし箇条書き部分は「進め！キノピオ隊長」のRTAのAny%カテゴリーにおいて具体的に対応しているものを、それぞれ記載します。

1. ゲームソフトは複数のワールド（エピソード）からなる。最短タイムは、ワールド番号の小さいものから大きいものへという順番でクリアしなければ達成できない。

   • エピソード1～エピソード3

2. 各ワールドには複数のステージ（ページ）がある。最短タイムは、ステージ番号の小さいものから大きいものへという順番でクリアしなければ達成できない。

   • エピソード1には、1-01～1-18の18ページ
   • エピソード2には、2-01～2-18の18ページ
   • エピソード3には、3-01～3-28の28ページ

3. 各ステージには、1つあるいは複数の進行アイテム（ダイヤ）が配置されている。そのステージは進行アイテムを取得しなくてもクリアできる。

   • 各ページに、3つのダイヤ

4. 訪れてクリアをしなくてもよい（スキップしてもよい）ワールドやステージが存在してもよい

   • 1-06
   • （中略）
   • 3-26

5. あるステージをクリアすることで、アンロックされる1つないし複数のステージがある

   • 1-01をクリア → 1-02がアンロック
   • （中略）
   • 3-27をクリア → 3-28がアンロック

6. さらに、一部のステージを訪れるには、一定数の進行アイテム（ダイヤ）を取得済みである必要がある

   • 1-10を訪れるには、12個のダイヤが必要
   • （中略）
   • 3-27を訪れるには、155個のダイヤが必要

仮定

必要となる仮定を厳密に網羅して列挙することは難しいのですが、少なくともこれはなければならないと思われるものを列挙します。

1. ゲームソフトの進行構成をスキップできるようなバグは存在しない
2. 各ステージについて、進行アイテムを0個、1個、…、最大個取得する場合の最短クリアタイムは、それぞれわかっているものとする

適用範囲

仮定の2つ目が強すぎるというか、その部分の理論的な最短チャートこそ知りたいものだと思われるかもしれません。しかしながら、ステージ内においては、前述のように、操作の選択が発生する機会が1秒あたり数十回もあり、それらをゲームソフトのコードやそれが動くゲーム機の挙動と照らし合わせる必要があるため、ステージ内の動きについて理論的に最適なものを求めるのは困難です。

本記事では、各ステージ内でどう操作すればよいかはRTAプレイヤーによる試行錯誤で発見された一連の操作を（最適なものと仮定して）採用し、「どのステージをクリアないしスキップをし、クリアする各ステージでは何個の進行アイテムを取得するか」という部分の最適な選択を、数理最適化を用いて行います。

数理最適化によるステージ選択・進行アイテム取得

数理最適化には適用する対象に応じてさまざまな手法があります。本記事で扱う「進め！キノピオ隊長」のAny%カテゴリーのRTAにおける最適なステージ（ページ）選択と各ステージの進行アイテム（ダイヤ）取得数を導出できる手法もいくつかあります。どの手法を選んでも手計算ないしコンピューターで計算プログラムを動かすことになるので、計算時間が短くてすむ手法がよいです。そして、その手法が適用できるように、対象の捉え方を工夫する必要があります。

動的計画法の適用（今回の場合は、どちらかというと非巡回有向ネットワークに対するダイクストラ法）

本記事で行う工夫として、どのステージをクリアしたか、進行アイテムを何個所持しているかという、RTAの道中の「状態」と、プレイを進めてある状態から別の状態へ「遷移」することを考えます。そして、状態と遷移を表現するにあたり、数学の「グラフ理論」における「グラフ」を拡張した「ネットワーク」（リンク1、リンク2）というものを使用することにします（必ずしもネットワークで表現する必要はなく、漸化式や多次元の表を使用してもかまいません）。

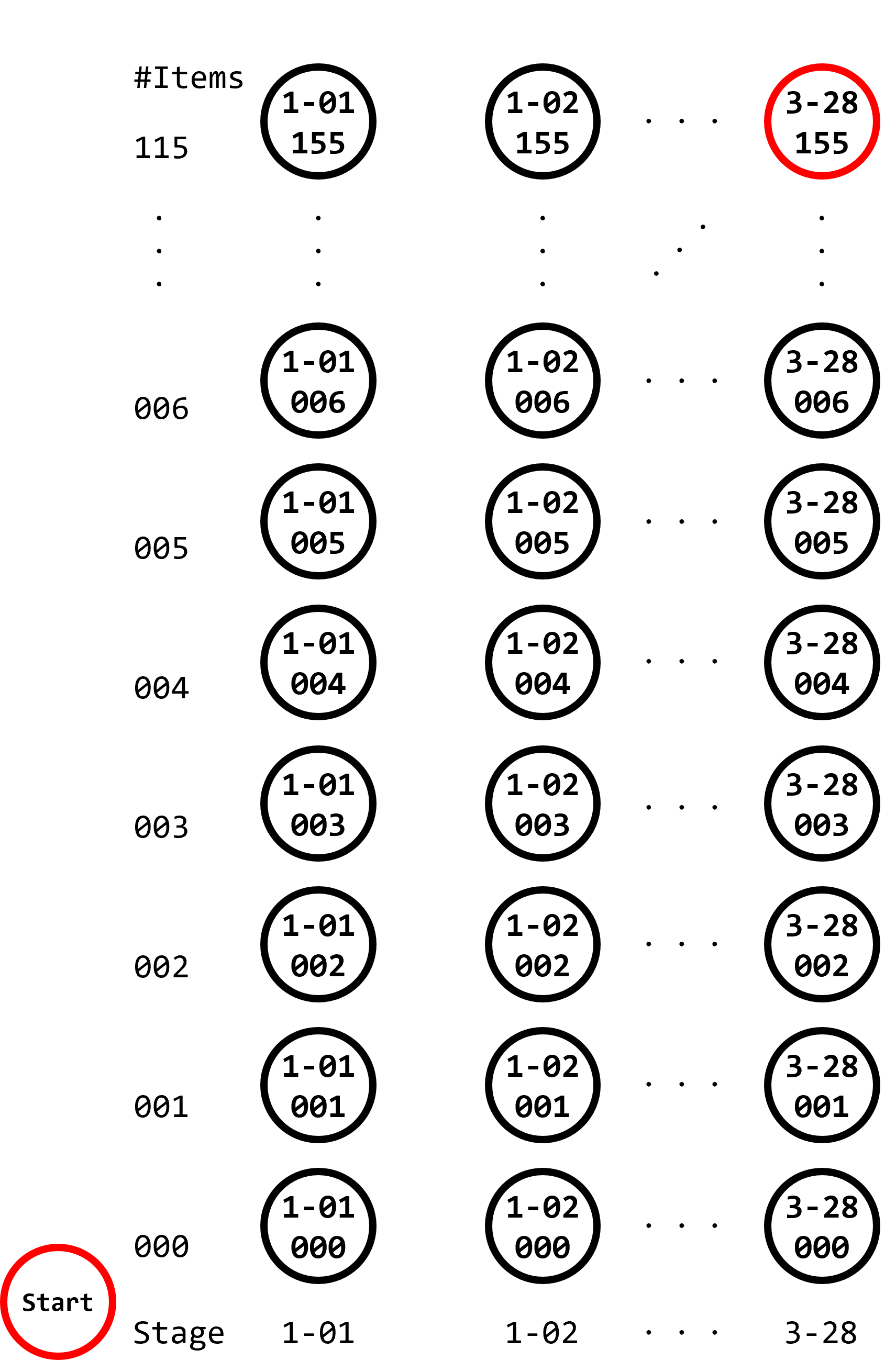
まず、状態として、RTAの「スタート」および、各ステージ（ページ）のクリア時点を考えます。ただし、同じステージのクリア時であっても、進行アイテム（ダイヤ）数の保有数に応じて状態を区別します。例えば、「1-01クリア時点、ダイヤ保有数0個」「1-01クリア時点、ダイヤ保有数1個」といったものです。Any%カテゴリーではダイヤを155個保有すれば3-28のゴール地点まで到達できますし、156個以上のダイヤを取得するには余計なタイムがかかるため、ダイヤ保有数は0～155までを考えます。以下に図例を示します。丸印が状態を表します。

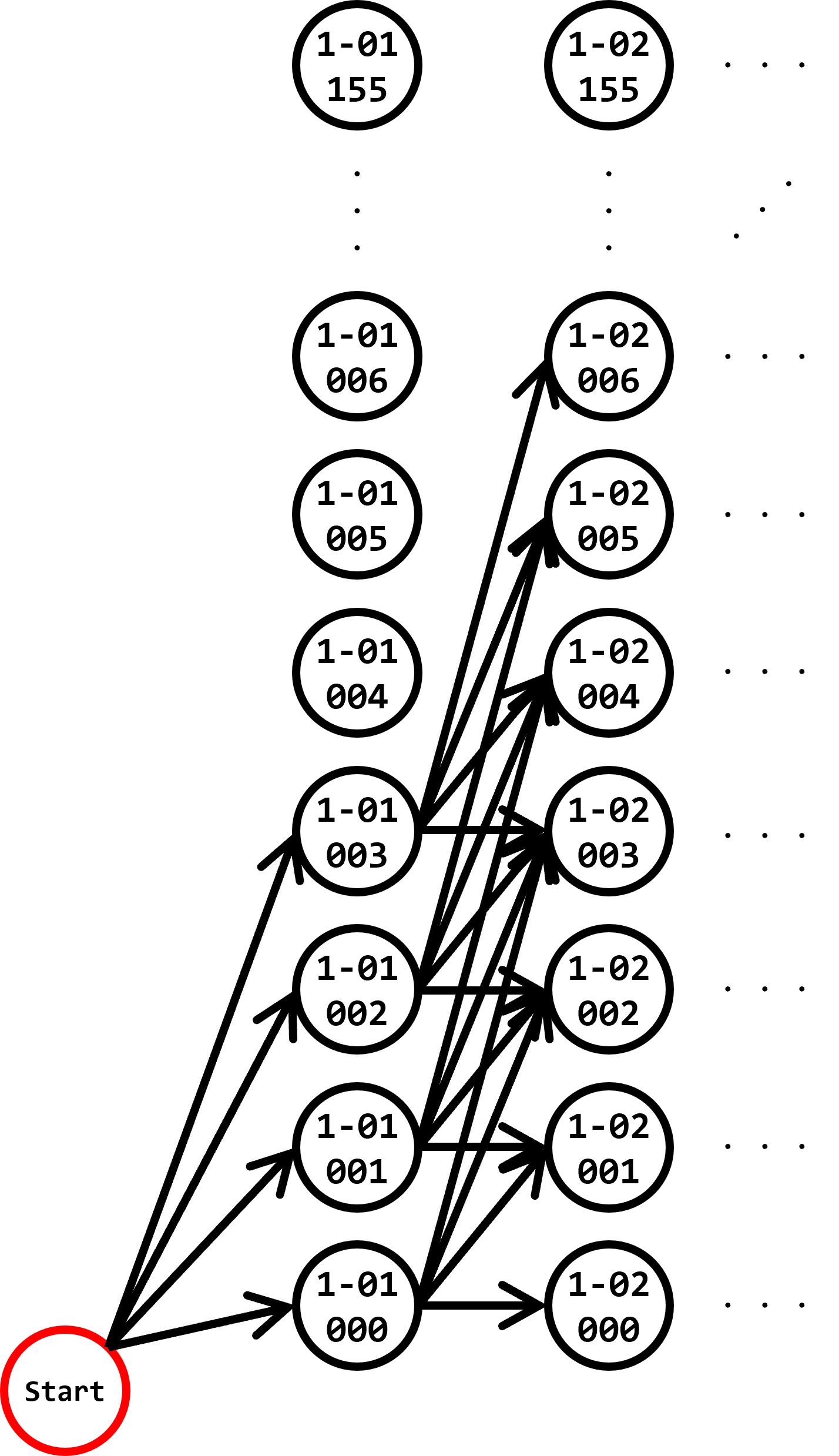
次に、状態間の遷移を、ゲームソフト中のいくつかの場面の例に挙げて考えます。まず、「スタート」から始めて次に遷移できる状態としては、その時点でアンロックされているステージ（ページ）が1-01しかなく、1-01で取得できる進行アイテム（ダイヤ）が最大3個なので、「1-01クリア時点、ダイヤ保有数0個」～「1-01クリア時点、ダイヤ保有数3個」までの状態に遷移できます。次に、1-01のクリアから次に遷移できる状態ですが、1-01をクリアすると1-02がアンロックされ、1-02でもダイヤを0～3個取得することができるため、「1-01クリア時点、ダイヤ保有数0個」からは「1-02クリア時点、ダイヤ保有数0個」～「1-02クリア時点、ダイヤ保有数3個」までが、（中略）、「1-01クリア時点、ダイヤ保有数3個」からは「1-02クリア時点、ダイヤ保有数3個」～「1-02クリア時点、ダイヤ保有数6個」までが、それぞれ可能です。以下に図例を示します。矢印が遷移を表します。

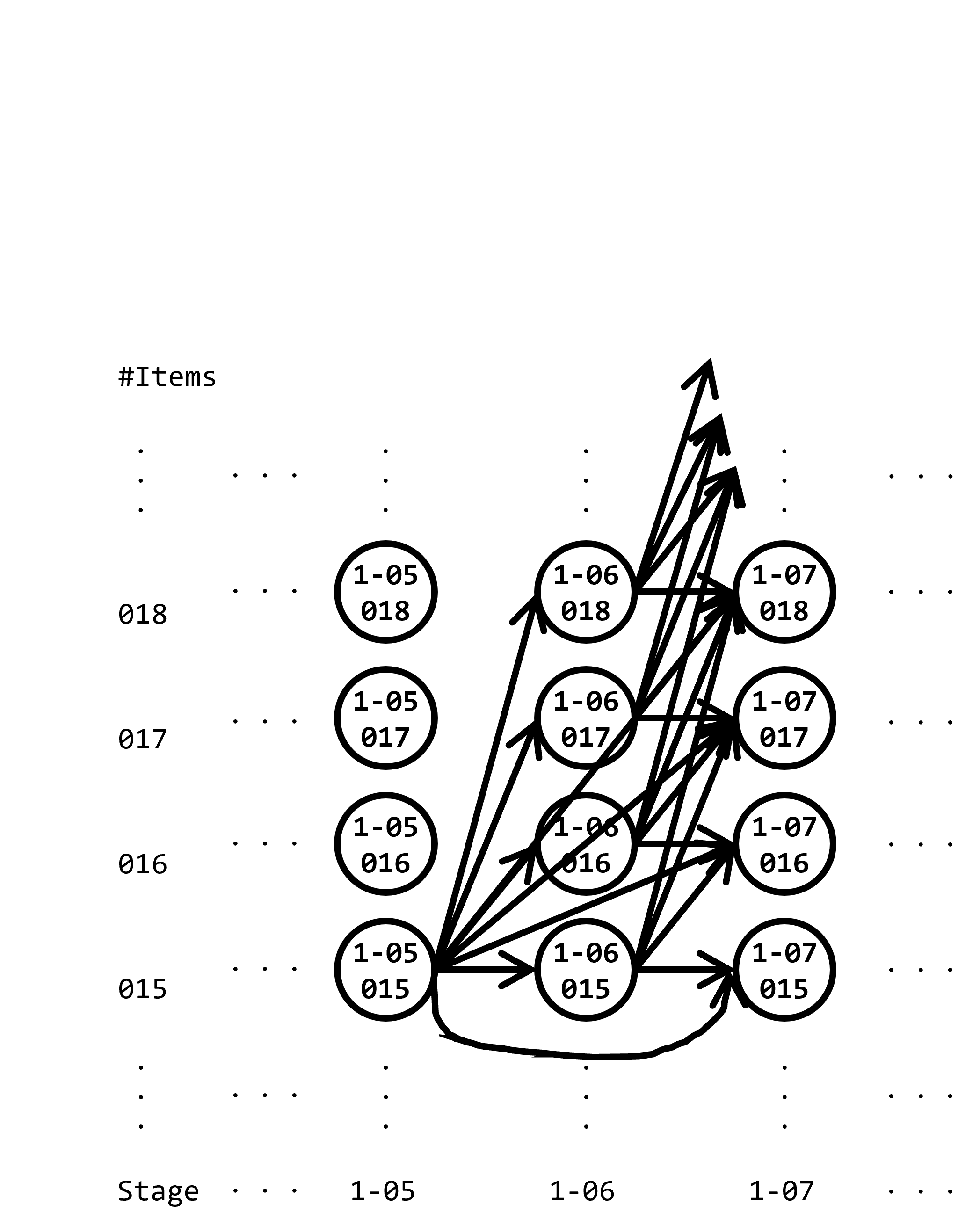
別の例として、ここでは保有ダイヤ数については説明を省略しますが、1-05をクリアすると1-06と1-07がアンロックされるため、1-05からは1-06と1-07の両方への遷移ができます。一方、1-06をクリアしてもどのページもアンロックされませんが、次に1-07を訪れることができるため、1-06から1-07に遷移ができます。似た例として、2-10をクリアすると2-11、2-12、2-13がアンロックされ、2-11と2-12はクリアしてもアンロックされるページがないという場面を挙げます。このとき、2-10からは2-11、2-12、2-13へ、2-11からは2-12、2-13へ、それぞれ遷移が可能です。ここで、2-12についてですが、2-12をクリアした後に2-11を訪れることはプレイ上は可能なものの、2-11をクリアした後に2-12を訪れたほうがゲームソフトのUI操作に要する時間が短いため、2-12から2-11への遷移はないものとします。ゲームソフトの進行構成のところで述べた、最短タイムはワールドやステージ番号の小さいものから大きいものへという順番でクリアしなければ達成できないという特徴の一例が、これにあたります。1-05～1-07について、以下に図例を示します。なお、1-05クリア時点では、保有ダイヤ数は最大で15個です。

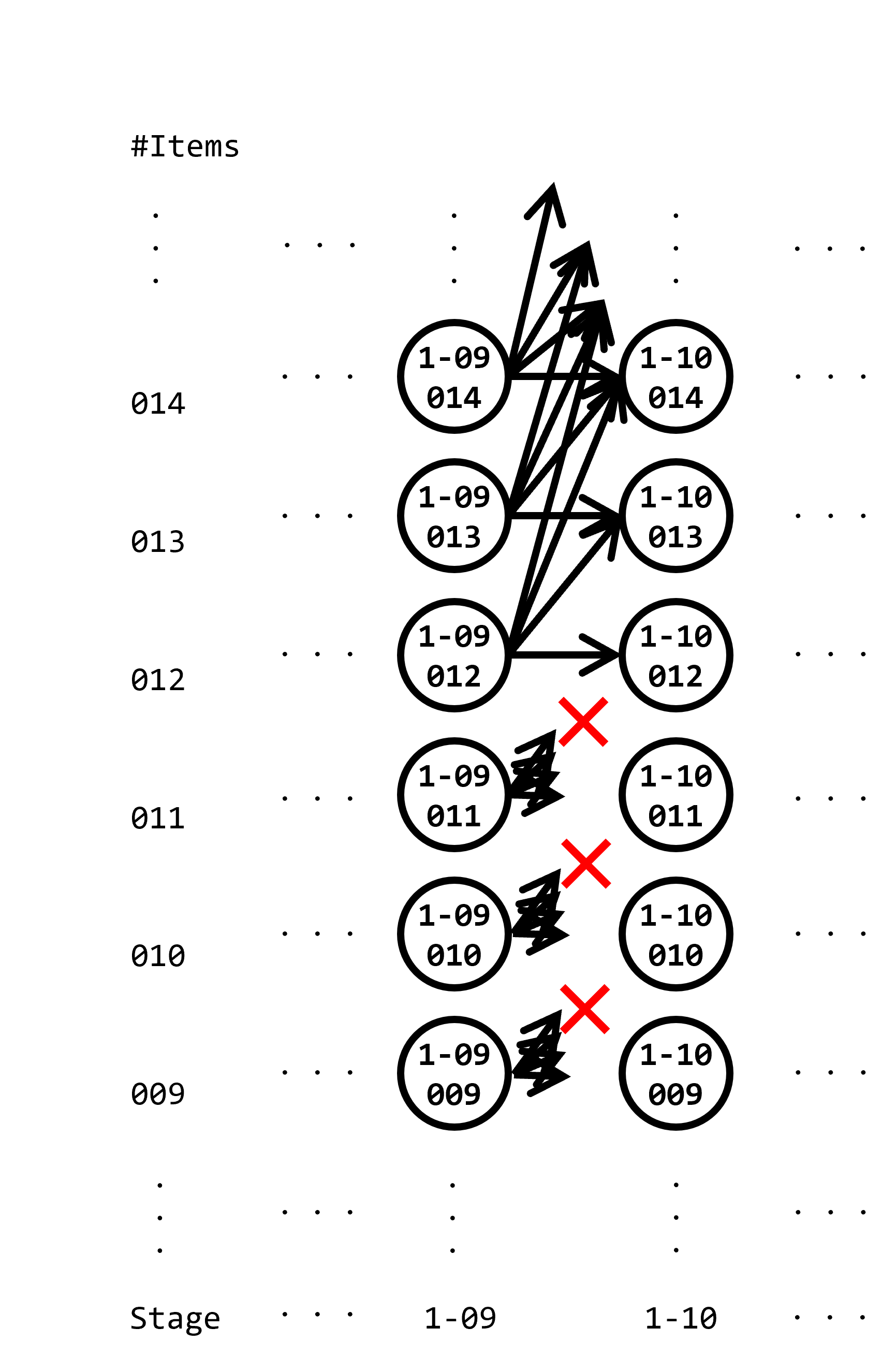
ほかの例として、1-10への遷移を考えます。1-10を訪れるには12個のダイヤが必要のため、1-09クリア時点で（あるいは、1-09はスキップできるので、そうする場合は1-08クリア時点で）12個以上のダイヤを保有している必要があります。なので、「1-09クリア時点、ダイヤ保有数0個」～「1-09クリア時点、ダイヤ保有数11個」という状態たちは、遷移先がありません。似た例として、1-18を訪れるには30個のダイヤが必要のため、「1-17クリア時点、ダイヤ保有数0個」～「1-17クリア時点、ダイヤ保有数29個」という状態たちは、遷移先がありません。1-09と1-10について、以下に図例を示します。

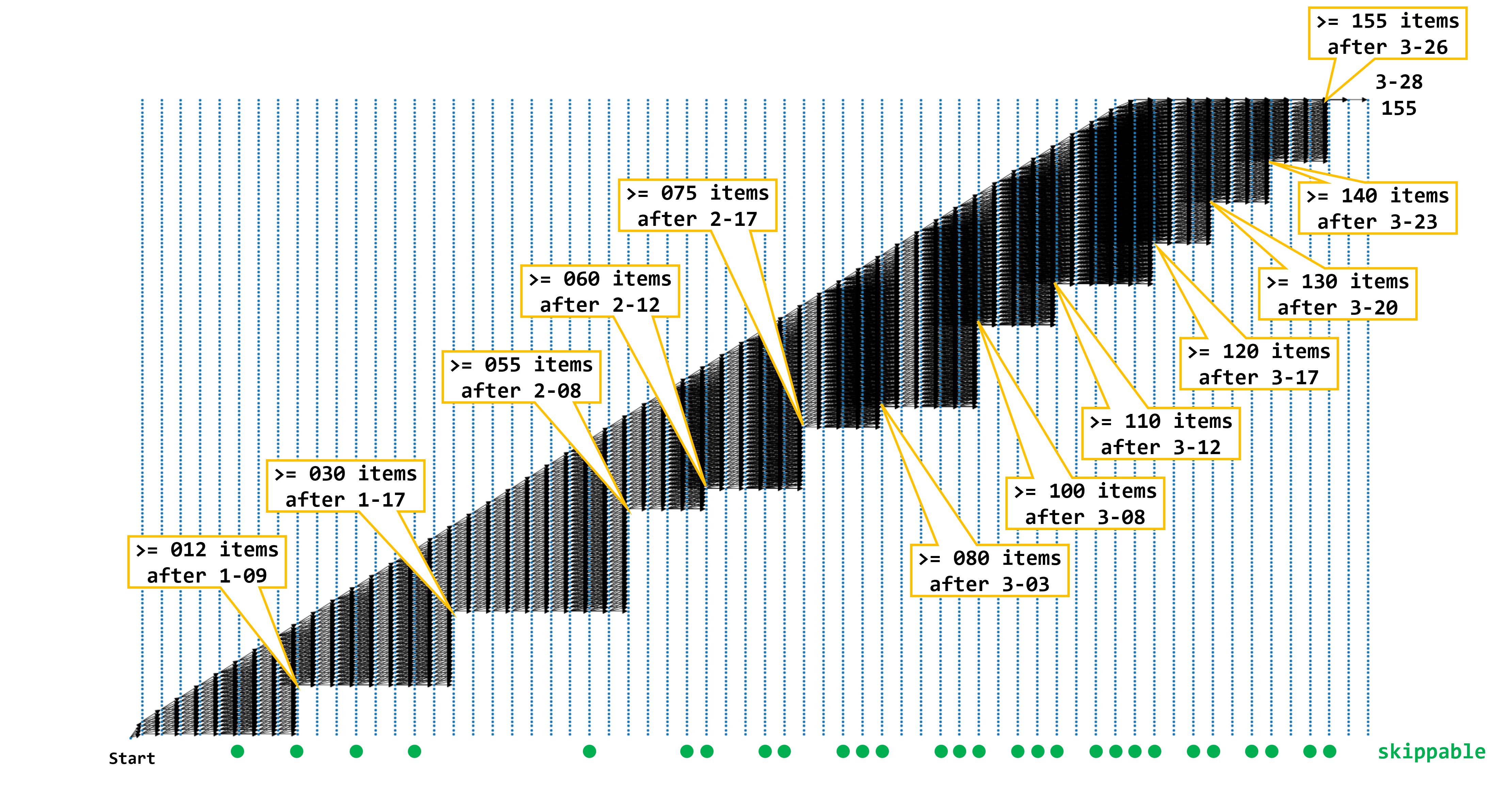
状態と可能な遷移を網羅的に列挙して可視化したのが、下の図になります。これまでの図と同様に、横軸がStartから始まり1-01, 1-02, ..., 3-28までのステージの並び、縦軸が0から始まり1, 2, ..., 155までの進行アイテム累計取得数を表します。緑の丸がついているステージは、スキップ可能なステージです。たくさんあって見えづらいですが、「Start」から「3-28 155」へとつながる黒矢印全体が、ゲーム開始からAny%カテゴリークリアまでのチャートを構成します。例えば、「Start」から右上にまっすぐ伸びていく推移は、スキップ可能なステージを含む全ステージを訪れ（155つに達するまで）各ステージで進行アイテムを3つ取得することを表しています。図の下側が階段状に見えるのは、階段になっているステージのクリア時点で一定数以上の進行アイテムを取得していなければ先に進むことができないことを表しています。

次に、各遷移（上図の一つ一つの矢印）について、仮定により判明している最短クリアタイムをひも付けます。例えば「スタート」から「1-01クリア時点、ダイヤ保有数0個」への遷移には、エピソード1のプロローグでキノピオ隊長を動かし始めてから、1-01でダイヤを全く取得しないでクリアするまでのタイムを付与します。実際には、自分自身のプレイ、あるいは、ほかのRTAプレイヤーの動画から、タイムを計測することになります。遷移元の状態における保有ダイヤ数の違いによって遷移先のステージのクリアタイムが変わることはないため、全ページについてダイヤを0個取得した場合のタイム～ダイヤを3個取得した場合のタイムと、UI上でページを1つや2つなどめくってほかのページに移動するのにかかるタイムを計測すれば、全ての遷移に対してタイムがひも付けられます。

状態と遷移、そして各遷移にかかる時間をネットワークで表現することで、「進め！キノピオ隊長」のAny%カテゴリーのRTAを最短時間で実現し得るステージ（ページ）選択と進行アイテム（ダイヤ）取得は、数理最適化の中の「動的計画法」（リンク1、リンク2、リンク3）という手法、あるいは、「（非巡回有向ネットワークに対する）ダイクストラ法」という手法により、求めることができるようになります（繰り返しになりますが、必ずしもネットワークで表現してダイクストラ法を適用する必要はなく、漸化式や多次元の表を使用して考えてもかまいません）。本記事の説明は、どちらかというと後者寄りです。「ダイクストラ法」（リンク1、リンク2）は、カーナビが現在位置から目的地まで最短時間で到着できる道路の経路を求めたり、鉄道の乗り換え案内サービスがある駅からある駅まで最短時間で移動する列車や乗り換えの経路を求めたりする際に使用できる手法です。本記事で表現したネットワークにダイクストラ法を適用して、「スタート」という状態から「3-28クリア時点、ダイヤ保有数155個」という状態までの累計タイムが最短になる遷移を求めることで、「進め！キノピオ隊長」のAny%カテゴリーのRTAにおいて、どのページを訪れ、各ページではいくつのダイヤを取得することが最適なのかが、明らかになるわけです。

本来ならば、ここから動的計画法、ないし、（非巡回有向ネットワークに対する）ダイクストラ法の内容を紹介すべきなのですが、本記事の執筆者はここまでの記事執筆で力尽きてしまいました。申し訳ありません。本記事から貼られている各手法のリンクの先のウェブページは、理論的にやや厳密な記述が多いため、手法名を検索エンジンにかけて表示される別のウェブページをご覧になったほうが、理解しやすいかもしれません。

なお、本記事で紹介した手順とはやや異なりますが、「ナップサック問題」（リンク1、リンク2）を動的計画法で解くことも参考になります。

(2022-12-19: 追記)
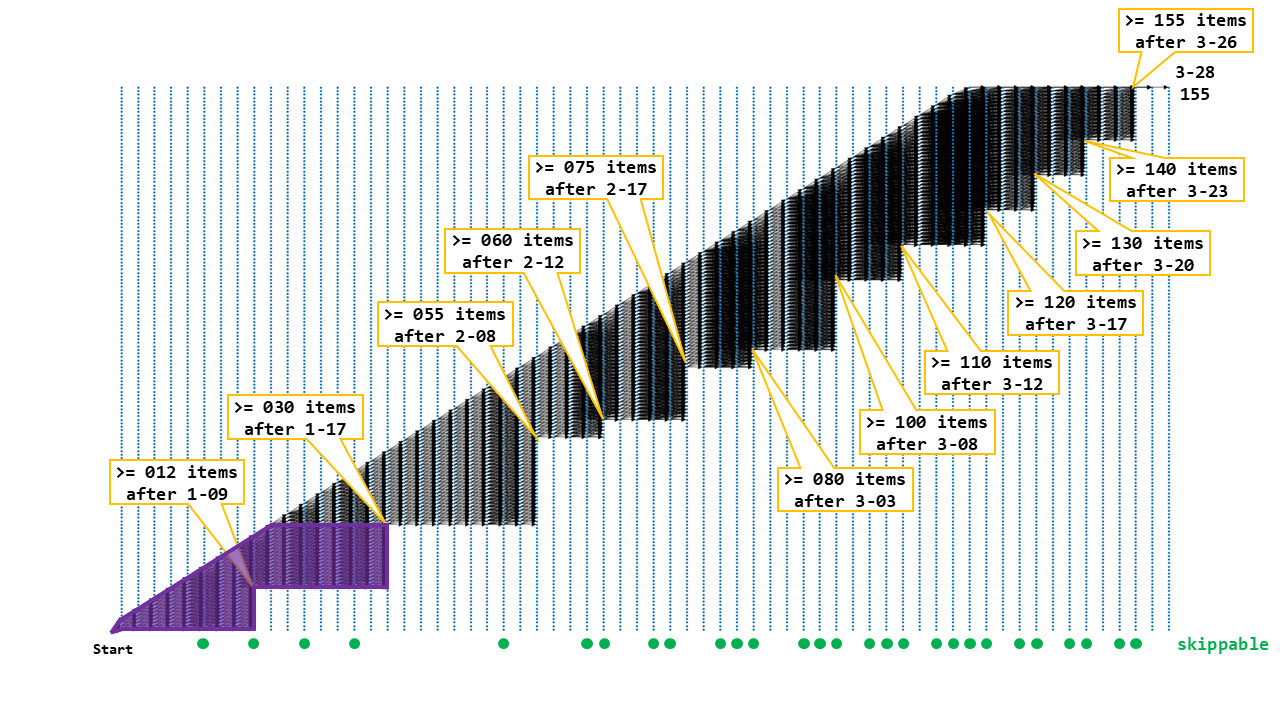
ちなみに、Any%カテゴリークリアまでのチャートとして取り得る推移が全部で何通りあるか、プログラムを書いてコンピューターに数え上げさせようとしましたが、膨大な数になるようで、正確な数はわかりませんでした。その代わり、ワールド（エピソード）1クリアまでを対象とする、つまり、「スタート」という状態から「1-17クリア時点、ダイヤ保有数30個」という状態までチャートとして取り得る推移（下の図の紫で囲った範囲）を数え上げさせたところ、1,660,552,560通りになりました（数え上げにかかった計算時間ですが、Python言語で（メモ化などをしない）単純な「深さ優先探索」（リンク）を実装し手元のPCで動かして3, 4時間程度でした）。Any%カテゴリーでは続けてエピソード1と同等以上のページ数とダイヤ数があるエピソード2とエピソード3をクリアしなければならないため、Any%カテゴリークリアまでのチャートとして取り得る推移の総数は少なく見積もっても10億の3乗通りになります。最適チャートを求めるのに単純な全探索では難しく動的計画法などにより効率的に求めなければならないことがわかりますね。

プログラミングコード

「進め！キノピオ隊長」のAny%カテゴリーで登場するステージ（ページ）数・進行アイテム（ダイヤ）数であれば、手計算でもできるのですが、面倒なのでプログラムを書いてコンピューターに計算させます。Python言語で実装したものを、以下に置いています。

動的計画法というよりかは非巡回有向ネットワークに対するダイクストラ法に近い実装になっております。また、Python/Codes/main.pyのnum_strategies: int = 1という変数の値を変えることで、1番目～num_strategies番目に最適なチャートまでを出力するようになっています（第num_strategies最適なチャートまで求める部分の実装には、ダイクストラ法で各頂点が保有するラベル数を1つではなくnum_strategiesつにするという素朴な拡張を採用しています）。

(2022-12-25: 追記)
プログラムを久々に見返したのですが、 実装がいけていない箇所として、以下の2つがあることを思い出しました。 恥ずかしい実装があったので修正しました。

• 非巡回有向ネットワークの場合は、ダイクストラ法でラベルを確定する頂点を選ぶ部分について、頂点のトポロジカル順序の順に選ぶことができますが、(面, ダイヤ数)ペアの辞書式順はトポロジカル順序の条件を満たしているので、面とダイヤ数の2重のfor文により順番に頂点を選択する実装にしました
• 各頂点が保有するnum_strategiesつのラベルを格納するデータ構造として、Python言語組み込みのheapqを使用する実装にしました

↓ いけてない実装だったときの言い訳

• (面, ダイヤ数)ペアの辞書式順はこのグラフのトポロジカル順序の条件を満たしているので、頂点の探索順を(面, ダイヤ数)ペアの辞書式順としているが、探索順を求めるのにPython言語組み込みの優先度付きキューを採用している（これを採用しても(面, ダイヤ数)ペアの辞書式順に頂点が選ばれる）
  • 本来ならば面, ダイヤ数の2重のfor文で回すのがよい
• 各頂点が保有する num_strategies つのラベルを格納するデータ構造として言語組み込みの配列を採用し、要素を並び替えるのにも言語組み込みのソート機能を使っている
  • 本来ならば連結リストにでもしたうえで、ソートの箇所は自前で整列したほうがよい

「進め！キノピオ隊長」のAny%カテゴリーのインスタンスサイズは大きくないことから、いずれも面倒くさがって自前での実装をサボり、計算量が増えることには目をつぶって言語組み込みの機能を使っていました。プログラム内の該当箇所にはコメントを記載しました。

入力データについて、仮定で述べた「各ステージについて、進行アイテムを0個、1個、…、最大個取得する場合の最短クリアタイム」、および、UI上でステージ間を移動するのにかかるタイムは、本記事の執筆者のプレイに基づく値を入れています。現状、世界で最も速くクリアするプレイヤーのタイムではないことにご注意ください。タイムははおおむね0.5秒単位の精度で計測しています。なお、どの状態の遷移をたどっても共通して発生する部分（幕あいのアニメーションなど）のタイムは、計測から省いています。「9017.00」という数値が入っているところがありますが、これは対応する状態が最適なステージ選択・進行アイテム取得数の遷移の列に明らかに含まれないことがわかるため（例えば、訪れてクリアをしなくてもよいステージを進行アイテムを取得せずにクリアするよりも、そのステージを訪れないことのほうが、タイムは短くなるため、訪れてクリアをしなくてもよいステージを進行アイテムを取得せずにクリアすることはない）、計測を行わず、代わりに適当に定めた大きな値を入れていることを表しています。

入力データの例を以下に示します。1つ目の図は、各ページについて、そのページを訪れるのに必要なダイヤ数（必要ない場合は空白）、そのページでダイヤを0個、1個、2個、3個取得する場合のクリアタイム、そのページをクリアするとアンロックされるステージのリストです。

2つ目の図は、UI上でページ間を移動するのにかかるタイムです。

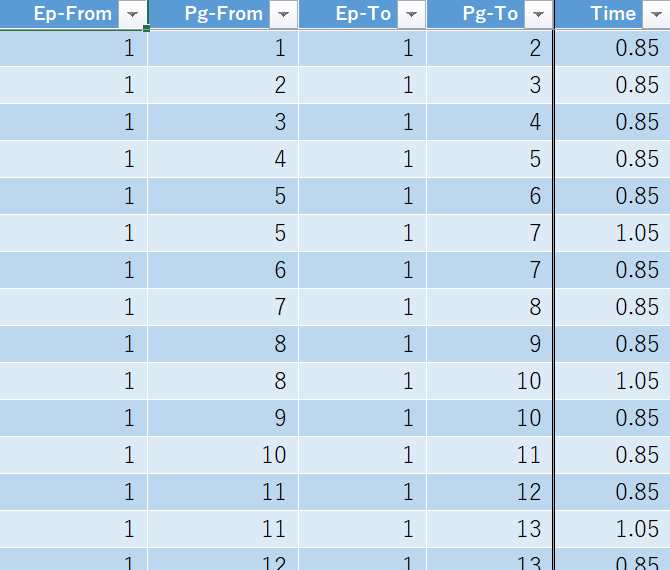
この2つの図のタイムを足したものが、ある状態からある状態への遷移に付与されるタイムになります。例えば、「1-01クリア時点、ダイヤ保有数0個」から「1-02クリア時点、ダイヤ保有数3個」、「1-01クリア時点、ダイヤ保有数1個」から「1-02クリア時点、ダイヤ保有数4個」、「1-01クリア時点、ダイヤ保有数2個」から「1-02クリア時点、ダイヤ保有数5個」、「1-01クリア時点、ダイヤ保有数3個」から「1-02クリア時点、ダイヤ保有数6個」への遷移には、共に0.85 + 50.50 = 51.35という値が付与されます。

計算結果

最適なステージ選択・進行アイテム取得数は以下のようにでました。数値が表しているのは「ワールド名-ステージ名(ステージクリア時の累計進行アイテム数)」です。結果を見る際に注意しなければいけないのは、入力データとして本記事の執筆者のプレイに基づく値を採用しているので、本記事の執筆者にとって最適なチャートであるということです。

1-01(003) -> 1-02(006) -> 1-03(009) -> 1-04(012) -> 1-05(015) -> 1-07(018) -> 1-08(021) -> 1-10(024) -> 1-11(027) -> 1-12(030) -> 1-13(033) -> 1-14(036) -> 1-15(039) -> 1-16(042) -> 1-17(045) -> 1-18(048) -> 2-01(051) -> 2-02(054) -> 2-03(057) -> 2-04(060) -> 2-05(062) -> 2-07(065) -> 2-08(068) -> 2-09(071) -> 2-10(074) -> 2-11(077) -> 2-12(080) -> 2-13(083) -> 2-14(085) -> 2-16(088) -> 2-17(090) -> 2-18(093) -> 3-01(096) -> 3-02(099) -> 3-03(102) -> 3-04(105) -> 3-05(108) -> 3-06(111) -> 3-07(114) -> 3-08(117) -> 3-09(120) -> 3-11(123) -> 3-12(126) -> 3-13(129) -> 3-15(132) -> 3-17(135) -> 3-18(138) -> 3-20(140) -> 3-21(143) -> 3-22(146) -> 3-23(149) -> 3-24(152) -> 3-25(155) -> 3-27(155) -> 3-28(155)

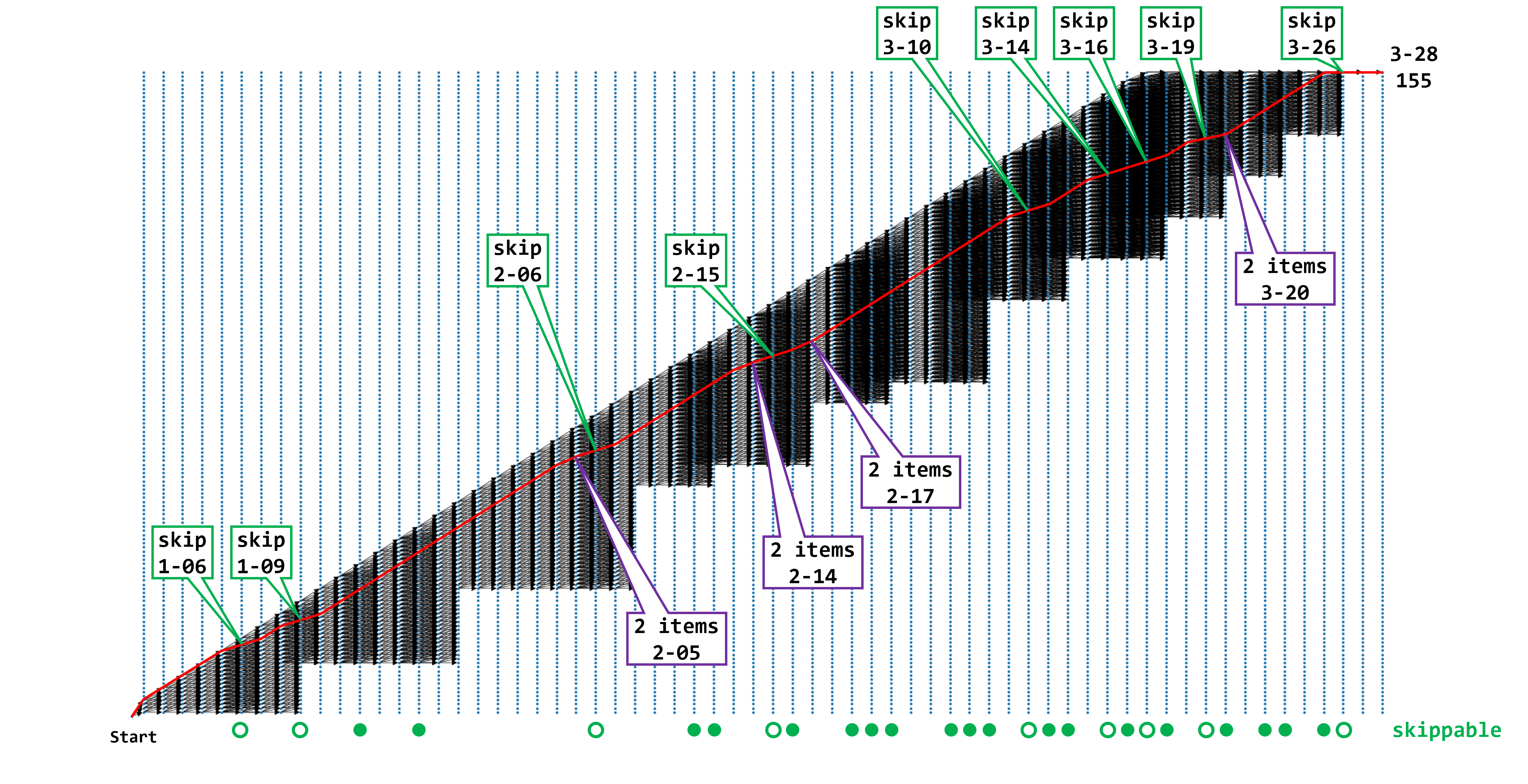
状態と可能な遷移を網羅的に列挙して可視化したものの上に最適チャートをプロットすると、下の図のようになります。簡単でクリアに時間がかからない序盤のステージでダイヤを多く取得することがわかります。一方で、スキップするステージは序盤・中盤・終盤からまんべんなく選ばれています。

第1最適チャート～第6最適チャートまでの順位と、特に着目すべきチャートの順位を計算してみました。タイム差と、各チャートでステージ選択・進行アイテム取得数が異なるところをピックアップしたのが下の表です。「×」は、そのステージを訪れないことを表します。

(2022-04-06: 計算結果を改訂)
3-03でダイヤを3つ取得してクリアするタイムを改善したので、GitHubのリポジトリーのデータを更新(v1.2としてリリース)して再計算したところ、大きく結果が変わりました。

順位	1位とのタイム差	1-06	1-11	2-10	2-17	3-03	3-12	3-14	3-20	3-26	備考
1	---	×	3	3	2	3	3	×	2	×	2022-04-06時点での世界記録のチャート
2	+ 3.5 s	×	3	2	3	3	3	×	2	×
2		×	3	3	3	3	×	2	2	×
2		×	3	3	2	3	×	×	2	3	2022-04-06時点での本記事の執筆者のチャート
5	+ 5.5 s	×	2	3	3	3	3	×	2	×
6	+ 7.0 s	×	3	2	3	3	×	×	2	3
...	...	...	...	...	...	...	...	...	...	...
19	+ 10.5 s	×	3	3	2	3	3	2	×	×
19		3	3	3	2	3	×	×	2	×
...	...	...	...	...	...	...	...	...	...	...
29	+ 11.5 s	×	3	3	3	x	3	2	2	x
...	...	...	...	...	...	...	...	...	...	...
57	+ 14.0 s	×	3	3	2	3	×	2	×	3

計算を行った2022-04-06時点での世界記録のチャートは第1最適である計算結果になりました。ところで、新たにRTAを始めるプレイヤー向けに有志が作成したガイドというものが複数あり、そこでは、2022-04-06時点での世界記録のチャートをベースにして、オプションの選択肢として「1-06（ダイヤ3つ取得）」「3-14（ダイヤ2つ取得）」「3-26（ダイヤ3つ取得）」を訪問することも提示されています。上記の第6最適までのチャートと照らし合わせると、3-12を3-26に変えること（=本記事の執筆者が2022-04-06時点で採用しているチャート）が、第2最適タイ(1位とのタイム差は3.5秒)という結果になりました。一方で、3-20を3-14に変えるのは全体の中では第19最適(1位とのタイム差は10.5秒)であり、あまりよいチャートとは言えません。3-20でダイヤを2つ取得しつつ短時間でクリアするにはテクニックがいるのですが、身につければ非常に効果が大きいことがわかります。また、1-06を訪れるチャートの中で最もよいものも第19最適(1位とのタイム差は10.5秒)という結果になっており、1-06を訪れるのもあまりよいチャートとは言えません。一方、ガイドでは触れられていない選択肢として「2-10でダイヤを3つではなく2つ取得し、2-17でダイヤを2つではなく3つ取得する」「2-17でダイヤを2つではなく3つ取得し、3-14を訪れダイヤを2つ取得する」というものが第2最適タイ(1位とのタイム差は3.5秒)として計算により発見されています。

さて、執筆者がこの結果を見て、今後、第1最適なチャートを採用するか否かですが、結論としては、採用しません。理由は、3-12ではダイヤを取得するためにゲームコントローラーのアナログスティックを使って的当てのようなことを行わなければならないのですが、執筆者の場合、短時間でできる場合もあればかなり時間がかかる場合もあり、タイムが大きくぶれやすいためです。では第2最適タイである3つのチャートの中で、現在採用しているチャート（いちばん下）以外のものはどうでしょうか。3つのうち、いちばん上のものは3-12を訪問を訪問するので採用しませんが、真ん中の「2-17でダイヤを3つ取得する、3-12を訪れない、3-14を訪れる、3-26を訪れない」は、検討に値すると思います。ですが、現在採用しているチャートと比べて安定性が増すようには感じられないので、しばらくは現在のチャートのもとでタイムを詰めていこうと考えています。

(2022-12-21: 追記)
第1最適チャートと執筆者の採用している第2最適チャートでステージ選択が異なる部分について、サンプルとしてクリアタイムを計測してみました。計測にはゲーム内である条件を満たすと現れるカウントアップタイマーを使用しました。そのため、入力データとは値が異なっており、粒度も1秒単位となっています。
平均値・中央値とも第1最適チャートのほうがわずかに上回るという結果がでましたが、やはり3-12はクリアタイムがブレてますね。この結果を受けて執筆者ももう一度考えたのですが、Any%カテゴリーでクリアしなければならないステージ数が58あり、ほかにも（難しかったり、乱数要素があったりで）タイムがブレやすいステージがあることを思うと、心理的なプレッシャーを1つでも減らすために第2最適チャートのほうを引き続き採用するという結論は変えません。

ステージ（ページ）	1回目	2回目	3回目	4回目	5回目	(平均値)	(中央値)	(最大-最小)
3-12 (第1最適)	50 s	54 s	51 s	47 s	49 s	50.2 s	50 s	7 s
3-26 (第2最適)	51 s	51 s	51 s	51 s	51 s	51.0 s	51 s	0 s

(2022-12-26: 追記)
3-12と3-26をクリアする様子のサンプル動画を作成しました。2022-12-21の追記（↑）では「結論は変えない」と書きましたが…？
https://twitter.com/samuelladoco/status/1607405267339350016

ほかに着目すべき点として、3-03を訪れないチャートで最もよいものは第29最適タイ(1位とのタイム差は11.5秒)という結果になりました。3-03でダイヤを3つ取得してクリアするタイムを改善したことで、3-03を訪れないという選択肢はなくなりました。筆者が以前採用していた「3-12を3-26に変え、3-20を3-14に変える」チャートは第57最適タイ(1位とのタイム差は14.0秒)という計算結果がでました。

(2022-09-09: 追記)
執筆者が2022-04-06時点で採用していたチャートで継続的にRTAを行ったところ、Speedrun.com上で世界記録を樹立することができました(下図)。

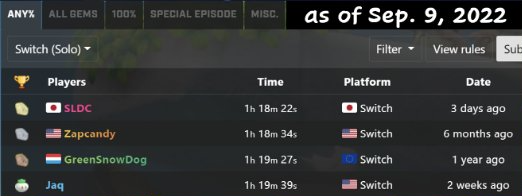
(2022-12-15: 追記)
同じチャートでさらに継続的にRTAを行ったところ、世界記録を1h18m01sに更新できました。

(2022-12-11: 追記)
このゲームのほかのRTAプレイヤーの記録で選択されたチャートに目を向けると、執筆者がプレイしているSwitch版の2～4位の記録(上図)、および、Wii U版の1位の記録では、第1最適チャートが採用されています。第1最適チャートで登場する3-12（ダイヤ3つ取得）について、最短タイムでクリアする場合と記録で実際にかかったタイムを比較しました。また、3-26（ダイヤ3つ取得）は何度やってもほぼ毎回、最短タイムでクリアできるので、それとも比較しました。結果を下表に示します。3-12を選択してよかった場合もあれば、そうでなかった場合もありますね。

記録	3-12を最短タイムでクリアする場合との差	3-26を最短タイムでクリアする場合との差
Switch版2位の記録	+ 1.0 s	- 2.5 s
Switch版3位の記録	+ 3.5 s	0.0 s
Switch版4位の記録	+ 1.0 s	- 2.5 s
Wii U版1位の記録	+ 9.5 s	+ 7.0 s

一方、Switch版の5位やWii U版の2～4位の記録では、執筆者と同じチャートが採用されています。ただし、Wii U版の3-26はSwitch版とコース形状やギミックが異なり、3-26ではなく3-12を選択した場合に最大で1.5秒しか有利にならないため、3-26がより選択されやすくなっていると考えられます。

繰り返しになりますが、入力データとして使用したのは、現時点での本記事の執筆者のプレイに基づく各ステージのクリアタイムです。そのため、今後、執筆者が特定のステージをより短いタイムでクリアできるようになったり、このゲームのRTAプレイヤーによりあるステージをより短時間でクリアする操作法が発見された場合は、入力データを更新して、再度計算をする必要がでてきます。別の捉え方をすると、どこかのステージのクリアタイムが短くなれば、更新された入力データを使ってもう一度プログラムを動かすことで、最適なステージ選択・進行アイテム取得数をすぐに導出し直すことができると言えます。これは、RTAのチャート構築の一部に数理最適化とプログラミングを使うことにより生じる、大きな利点です。

なお、プログラムは手元のPCで動かしたのですが、第100最適解まで計算しても、処理時間は4秒程度でした。

発展

本記事では、各ステージについて、進行アイテムを0個、1個、…、最大個取得する場合のクリアタイムとして、それぞれ最短タイムだけを使用しましたが、代わりに数十回～数百回プレイした際のクリアタイムの分布を使用することが考えられます。クリアタイムの分布を離散確率分布にすることで、各ステージのクリアタイムのブレや難しい操作の成功率を考慮してステージ選択・アイテム取得を決定することができると予想します。数理最適化の中にはこのように確率を考慮して答えを出す手法もあるので、その場合にどのようなチャートが答えとしてでるか、興味があります。もしかしたら、本執筆者が現在採用しているチャートが最もよいという結果がでるかもしれません。また、失敗する可能性が少なく、かつ、それなりにタイムが速くなるチャート、RTA用語でいうところの「安定チャート」を求めることもできるかもしれません。安定チャートを求めることができれば、決められた持ち時間の中でクリアすることが求められるRTAのイベントに応募・出場する際に役に立つでしょう。

ほかのゲームソフトへの応用可能性

ほかのゲームソフトについて、「進め！キノピオ隊長」と同様に、ステージ選択と各ステージでのアイテム取得数の最適化を動的計画法（または、非巡回有向ネットワークに対するダイクストラ法）で求めることができるかを考えます。なお、世の中にはたくさんのゲームソフトがありますが、本記事の執筆者のゲーム知識の限界により、ここでは、最近のスーパーマリオシリーズ本編のみを考察の対象とします。

同じ手法が応用できそうなもの

最近の3Dマリオシリーズの中では、「スーパーマリオ 3Dランド」が、ゲームソフトの進行構成が「進め！キノピオ隊長」と近いので、同じ手法が適用できるのではないかと推測しています。ただし、番号の小さいワールドから大きいワールドへとワープが可能なシステムがあるので、ネットワークの構築方法を多少変更しなければならないのではないかと考えています。「スーパーマリオ 3Dワールド」も、キノピオ隊長ステージやミステリーハウスステージなど一部のステージはいつ訪れるかの自由度があり、ワールド間で相互に行き来できるワープもあるものの、全体としてはゲームソフトの進行構成が近いため、同じ手法が適用できる可能性はあるかもしれないと推測しています。

同じ手法が応用できなさそうなもの

一方、同じ最近の3Dマリオシリーズでも、「スーパーマリオ オデッセイ」や、「スーパーマリオ 3Dワールド ＋ フューリーワールド」内の「フューリーワールド」は、ゲームソフトの進行構成として、進行アイテム（ムーン、ネコシャイン）の取得場所をステージと捉えた場合、ステージの訪問順に大きな自由度があるため、「進め！キノピオ隊長」と同じ手法は適用できません。これらのゲームで、どの場所の進行アイテムをどの順で取得すれば最短時間になり得るかは、「Prize Collecting Traveling Salesman Problem (PCTSP)」として捉えることができるのではないかと推測しています。PCTSPは、ステージ数が多ければ高速なコンピューターを用いても現実的な時間内に最短時間となるルートを導出できませんが、Speedrun.comで設定されているカテゴリーのうち、フューリーワールド（Any%と100%の両方）はステージ（ネコシャイン）数が最大100であり、オデッセイのAny%はワールドごとに分割して考えることができ、各ワールドのステージ（ムーン）設置箇所数はAny%クリア前であれば少ないので、これらのカテゴリーについては最新のPCであれば現実的な時間内に最短時間となるルートを導出できるのではないかと予測しています。

最近の2Dマリオシリーズは、各ステージに進行アイテムとして「スターコイン」が複数ありますが、RTAのカテゴリーによって、スターコインを取らなくてもよいか、全て取らなければならないかのどちらかなので、本記事の手法は適さないのではないかと推測しています。

参考

(2022-12-22: 追記)
「クッキークリッカー100万枚RTA」でも動的計画法によりチャートを考えておられる方がいました！しかもこの方なんと、私と同じ日にRTA in Japan Winter 2022に出場されます。

余談

「進め！キノピオ隊長」で、キノピオ隊長が各ステージをクリアしたときに発する音声が「バーボン！」に聞こえます🍄