はじめに
CIM(Coherent Ising Machine)は、光の干渉や非線形増幅を利用して組合せ最適化問題を解くために設計された物理システムです。
実際のCIMは、光パラメトリック発振器(Optical Parametric Oscillator; OPO)という光学デバイスをベースにしています。
OPOはざっくり言えば、光を「増幅しながら二つの状態のどちらかに落ち着かせる」性質をもつ発振器で、この振る舞いがスピンの二値化(±状態)に対応します。
その動作は本来かなり複雑な連立微分方程式で記述されますが、根底にあるのは「二値的な安定点をもつ非線形ダイナミクス」というシンプルな構造です。
CIMは実機だけでなく、シミュレータによる再現・解析も活発に行われています。
シミュレータでの実装にも興味がある方は、手前味噌ですが cim-optimizer を用いたシミュレーション記事 もあわせてご覧いただければと思います。
本記事では、CIMがどのように二値的な組合せ問題を解くのか、その基本的な性質を、単純化されたモデル方程式を用いて数値的に確かめていきます。
この記事の実装コードは、Google Colab こちら から試せます。
モデル方程式 ― 簡略化した非線形ダイナミクス
CIMの振る舞いは、スピンを連続変数として扱ったイジングモデルとして近似的に表すことができます。
その最も基本的な形は、次のような方程式です(参考:Yamamoto et al. 2020)。
\frac{dx_i}{dt} = -(x_i^2 - a)x_i - \sum_j J_{ij}x_j
ここで、各記号は以下の通りです:
| 記号 | 意味 | 備考 |
|---|---|---|
| $x_i$ | ノード $i$ に対応する振幅(OPO出力の実数成分などの近似) | 時間とともに変化する連続変数 |
| $a$ | ポンプ強度または利得パラメータ | $a>0$ のとき発振が起こり、$\pm\sqrt{a}$ 付近で安定 |
| $J_{ij}$ | ノード間の結合係数 | 問題構造(イジング結合)を規定し、符号整列を制御する項 |
この式は、離散スピン変数 ($s_i = \pm1$) を連続変数 ($x_i$) に置き換えた近似モデルです。
各ノードは自分の状態を安定させつつ、結合項 ($J_{ij}$) を通じて互いに影響し合い、最終的に符号パターン(+と−の並び)が全体として落ち着く方向へと進みます。
結合度とのバランスが大事
結合 ($J_{ij}$) が強すぎると、自己安定化とのバランスが崩れて不安定になることがあります。
そのため、ここでの式はあくまでCIMの基本的な性質をざっくり再現した近似モデルとして見るのが自然だと思います。
実際のCIMでは、この結合部分にフィードバック制御を組み込むことで、バランスを保ちながら安定した動作を実現しています(参考:cim-optimizer 公式ページ)。
自己項 ― ±方向に安定化するしくみを見てみる
まず、他のノードとの相互作用を無視して、1つのノードが自分自身だけでどう安定するのかを考えます。
このときの方程式は次のように書けます。
\frac{dx}{dt} = -(x^2 - a)x = -x^3 + a x
この式は、変数 $x$ が「自分の状態(振幅)」を少しずつ変化させながら、最終的に安定な値に落ち着いていく様子を表しています。
実はこれは、次のポテンシャル関数(エネルギーのようなもの)の傾きとして書けます。
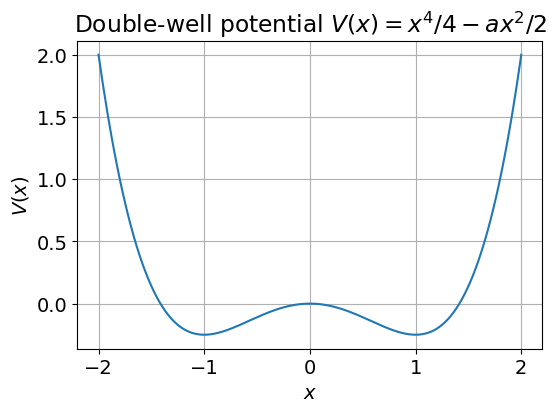
V(x) = \frac{1}{4}x^4 - \frac{a}{2}x^2
グラフで示すと以下のようになります。
この $V(x)$ は二重井戸ポテンシャルと呼ばれる形をしており、$x=0$ では不安定、$x=\pm\sqrt{a}$ では安定になります。
CIMではこの「$\pm\sqrt{a}$ の安定点」をスピンの「±1」状態として対応づけており、真ん中の 0 付近からはじめて、左右どちらかの谷(±状態)に落ち着くような動きをします。
エネルギー関数との関係
先ほどのダイナミクス:
\frac{dx_i}{dt} = -(x_i^2 - a)x_i - \sum_j J_{ij}x_j
は、次のエネルギー関数の勾配($x_i$ に関する偏微分)に基づいています。
E(\mathbf{x}) =
\sum_i \left( \frac{1}{4}x_i^4 - \frac{a}{2}x_i^2 \right)
+ \frac{1}{2}\sum_{i,j} J_{ij} x_i x_j
すなわち、
\frac{dx_i}{dt} = -\frac{\partial E}{\partial x_i}
となります。
ここで、エネルギー関数の各項の意味は以下の通りです:
| 項 | 役割 | 意味 |
|---|---|---|
| $\displaystyle \frac{1}{4}x_i^4 - \frac{a}{2}x_i^2$ | 自己ポテンシャル | $x_i = \pm\sqrt{a}$ に安定点を持つ二重井戸ポテンシャル。スピンが「±1」に落ち着く性質を連続的に再現。 |
| $\displaystyle \frac{1}{2}\sum_{i,j} J_{ij}x_i x_j$ | 結合エネルギー | ノード間の相互作用。イジングモデルの $\sum J_{ij}s_is_j$ に対応し、系全体の秩序を決める。 |
この $E(\mathbf{x})$ は、連続的なイジング系のエネルギー構造を再現したものと捉えられます。
第一項は、各ノードが ±方向に落ち着くようにする自己安定化ポテンシャルを表し、第二項はノード間の相互作用(結合) を表しています。
たとえば $x_i = \pm\sqrt{a}$ に落ち着くとき、第一項はその点で最小化され、安定な二値状態が得られます。
そのうえで第二項が、CIMにおける光学的な結合を反映し、ノード同士が“どのように符号を揃えるか”を決定します。
実際に試してみる
ここでは、CIMで見られるスピンの二値化挙動を、先に示した方程式をもとに実装してみます。
具体的には、
- ノード数:300
- 自己フィードバック係数:$a = 1$(各ノードが ±1 付近で安定)
- 結合行列 $J_{ij}$:平均0、標準偏差0.1のランダムな値
とします。
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams["font.size"] = 14
# === ランダム結合行列生成関数 ===
def make_random_dense_J(N, sigma=0.25, seed=0):
rng = np.random.default_rng(seed)
W = rng.normal(0.0, sigma, size=(N, N))
J = (W + W.T) / 2.0 # 対称化
np.fill_diagonal(J, 0)
return J
# === パラメータ設定 ===
N = 300
a = 1.0
dt = 0.01
steps = 5000
# === ランダム密結合行列 ===
J = make_random_dense_J(N, sigma=0.1, seed=42)
# === 初期値 ===
x = np.random.randn(N) * 0.1
x_history = [x.copy()]
E_history = []
# === エネルギー関数 ===
def energy(x, J, a):
term1 = np.sum(0.25 * x**4 - 0.5 * a * x**2)
term2 = 0.5 * np.sum(J * np.outer(x, x))
return term1 + term2
# === 時間発展 ===
for _ in range(steps):
dx = -x**3 + a*x - np.dot(J, x)
x += dx * dt
x_history.append(x.copy())
E_history.append(energy(x, J, a))
x_history = np.array(x_history)
E_history = np.array(E_history)
t = np.arange(steps+1) * dt
# === 可視化 ===
fig, axes = plt.subplots(2, 1, figsize=(8,7), sharex=True)
# (1) 振幅の時間変化
colors = plt.cm.PuOr(1 - np.linspace(0, 1, N))
for i in range(N):
axes[0].plot(t, x_history[:, i], lw=1, color=colors[i], alpha=0.95)
axes[0].set_ylabel("Amplitude $x_i$")
axes[0].set_title(f"Simplified CIM-like dynamics (N={N}, random dense J)")
axes[0].grid(True)
# (2) エネルギーの時間変化
axes[1].plot(t[1:], E_history, color="tab:purple")
axes[1].set_xlabel("Time")
axes[1].set_ylabel("Energy $E$")
axes[1].grid(True)
plt.tight_layout()
plt.show()
上図のように時間が経過すると、各ノードは自発的に ±1(a=1 のとき)付近へ落ち着きます。これは、自己安定化の力によって各ノードが自分を ±1 に保とうとするためです。
なお、実際に問題へ適用する際は、最後に sign(x) によって値を ±1 に変換します。この操作は、自己安定化項によってゼロ付近に滞在しにくくなる性質があるからこそ、はじめてこうした方法で値を決められるのだと思います。
補足:“揺らぎ”という最適化の入り口 ― 実際のCIMとの違い
ここまでのモデルは、エネルギーを下って安定するような理想的な系として描かれていますが、実際に研究されているCIMの理論モデルは、より複雑な構造をもっています。
私の現時点での理解としては、CIMでは方程式自体にノイズや揺らぎを時間的に変動させながら加えることで、局所解に収束するのを避けつつ、より良い解を探索しているのだと思います(参考:Leleu et al. 2018, 2021)。
また、Marandi et al. (2016) による実機を用いたCIMの研究では、どんな組み合わせ問題にも万能というわけではなく、特定の条件下では比較的解きやすいパターンも存在することが報告されています。
単純に考えれば、局所解が少ないシンプルな構造の方が探索しやすいのかもしれません。
最近は、実機による研究と理論モデルのかみ合いにも注目が集まっており、自然現象そのものが最適化を実現しているという点は非常に興味深く感じています。 私自身も、そうした仕組みを少しずつ学びながら理解を深めていければと思っています。
まとめ
本記事では、CIM(Coherent Ising Machine)の基本的なしくみを、できるだけシンプルな数式モデルで確かめてみました。
実際のCIMはもっと複雑で、ノイズや揺らぎを含みながら動いていますが、その中には“自然が自ら最適化を行う仕組み”が潜んでおり、それが現代のコンピュータによる最適化アルゴリズムにもつながる可能性を感じました。
これから少しずつ、そうした世界も探っていければと思っています。
この記事が、同じように興味をもつ方の何かのきっかけや参考になれば嬉しいです。