D-Wave Leapで簡単に量子アニーリングマシンに問題を解かせるようになったので、実際に使ってみました。ただ解くだけのはさみしいので、いろいろこじつけて実用を考えながら自然言語処理のToy問題を作ってやりました。
- 内容でいうと、word2vecで単語のグラフを作ってその上でmax cutやminimum vertex coverをD-Waveマシンにやらせました。
アニーリングマシンの原理はややこしいので個々では解説しません。ゲートマシンについてはこちらで基本的なことを解説しています。
D-Wave Leapについて
D-Waveの量子アニーリングマシンについて解説や学習資料、実際に動かすためのリソースなどをまとめたサービスです。詳細についてはこちらの動画がおすすめです。
D-Wave Leapに登録すると最初はいくぶんかの無料時間をもらえて実際にD-Waveのマシンで遊べます。初期特典は使わないとすぐ消えてしまいますが、gitのアカウントを登録すると月1分間だけ実行時間をもらえます。(自分がやった感じで)一度ハミルトニアンを作って計算させるとだいたい0.017秒程度消費するので、1分間あれば3000回試せます。遊ぶ分には十分かなと思います。お金で買うとなると今現在(2018年12月)1時間20万円、1分あたり350円ぐらいだそうです。ふむふむ。。。5分ぐらいなら買いたい気がします。
インストール、セッティング等
-
D-Wave Oceanを使います。
pipでイケます。 - 詳細についてはドキュメントが豊富です。
-
使い方の例もいろいろ載っているので、これを
パクって参考にしてやっていきます。 - D-Wave Leapのアカウントを使わずにシミュレータだけで解くこともできますが、実機で動かすにはこちらの手順でセッティングします。その際に必要となる
API endpoint URLとかAuthentication tokenとかsolverとかはログイン画面に載っています。
動かしてみる
何はともあれ、まずはやってみよう。
import networkx as nx
from dimod.reference.samplers import ExactSolver
import dwave_networkx as dnx
from dwave.system.samplers import DWaveSampler
from dwave.system.composites import EmbeddingComposite
# 実機で動かすためのもの
with open('./tk.txt') as f:
tk = f.readline().replace('\n', '')
sampler = EmbeddingComposite(DWaveSampler(token=tk, solver='DW_2000Q_2_1'))
sampler_sim = ExactSolver()
-
networkxはpythonでグラフと戯れるものです。 - dwave_networkxは
networkxで作ったグラフでdwaveの量子アニーリングマシンと戯れるものです。 - D-Wave Leapのアカウント登録がめんどくさいか登録にトラブった方は
sampler(実機を使う)の代わりにsampler_sim(シミュレータを使う)でこの記事のコードを実行できます。
と、いうことでグラフを作ります。
s5 = nx.star_graph(6)
nx.draw(s5, with_labels=True)
minimum vertex cover(最小被覆問題)問題を解いてみます。
- この点の集まり(ノードの集合)を取ればすべてのエッジが必ず集まりの中のどれかの点につながっている、というのは
vertex cover - vertex coverの中で点の数がもっとも少ないものは
minimum vertex cover
シミュレータで解きます。
dnx.min_vertex_cover(s5, sampler_sim)
[0]
0番目のノード、つまり真ん中の点が答えだそうです。はい、合っていますね。
次は実機で解きます。
res = dnx.min_vertex_cover(s5, sampler)
print(res)
[0]
おなじこたえになりました。
え、ちょっと拍子抜けですね。量子なんぞ知らんでも使えてしまう感じです。それでいいかどうかは別として、次はmax cut(最大カット)の問題です。
- この点の集まりを取れば、この点集まりの中の点とそれ以外の点をつなぐ枝が一番多い、そのような点の集まり(ノードの集合)をmax cutです
res = dnx.maximum_cut(s5, sampler_sim)
print(res)
{0}
res = dnx.maximum_cut(s5, sampler)
print(res)
{0}
はい!
タスクを実行するとD-Wave Leapの画面で実行記録とまだ使える実行時間を確認できます。
遊ぶ
グラフ理論のことは真面目に勉強したことがないですが、max cutの問題もminimum vertex coverの問題も、眺めていると、なんとな〜く全体のつながりのなかで重要な部分を選び出している感じがします。つながりの中で重要な部分を選びだせると言われれば、なるほど確かに物流・通信・金融・エンターテイメントなどのネットワーク問題に応用できそうな気がしてきますね。
word2vecについて
単語をベクトル表現に表現するやつです。
- 論文は1万回以上も引用されているというスゴイやつです。
- 目的の単語を周りの単語から予測したり、あるいは目的の単語を使って周りの単語を予測したり、「単語の意味はその文脈で決まる」という考え方に基づいて、すべての単語をベクトルに表現するものです。
- ムズカシイことはこちらの動画か、例の「ゼロから作るなんとか」本がおすすめです。
理論を知らなくても(理論はおもしろいけれど)使い方だけ覚えればひとまず事足ります。手軽に作るにはgensimがいいです。ここで使うモデルは予め日本語のwikipediaをコーパスにしてMecabとmecab-ipadic-neologdで分かち書きして作っておいたものです(ちなみに、gensimで日本語と戯れたい方におすすめな記事をふたつ、①対義語、②連想ゲーム、2つ目は下ネタ注意です)。
モデル
読み込み
from gensim.models import word2vec
import numpy as np
model_file = '../../nlp/models/wiki.model'
model = word2vec.Word2Vec.load(model_file)
wv = model.wv
warr = np.array(wv.index2word)
warr.shape
(221980,)
ちょっと、確認
wv.similar_by_word('サザエ')
[('ワカメ', 0.7819216251373291),
('マスオ', 0.7575982809066772),
('カツオ', 0.7378748655319214),
('タラオ', 0.7053970098495483),
('アワビ', 0.6775985956192017),
('鯛', 0.6705299615859985),
('アサリ', 0.6596939563751221),
('ハマグリ', 0.6487918496131897),
('鰯', 0.645553708076477),
('イクラ', 0.6388252973556519)]
こんな感じで単語の類似度を出せます。またベクトルなので足し算引き算ができます。
wv.most_similar(positive=['甥', '女'], negative=['男'])
[('姪', 0.7586474418640137),
('従弟', 0.7545753121376038),
('叔父', 0.7317503690719604),
('従兄', 0.7282092571258545),
('従兄弟', 0.7233381867408752),
('外孫', 0.7197000980377197),
('義弟', 0.7162268161773682),
('伯父', 0.7105128765106201),
('曾孫', 0.7003189921379089),
('従姉', 0.699201226234436)]
グラフ
ここではわかりやすくするために、比較的に少ない数の単語を使ってグラフを作ります。
word_list = np.array(['易', '理論', '製図', '計算', 'CAD', '算盤', '数学', '測量', '算', '大工', '集大成', '手本', '関数', '模範', '算術', '暗算', '釈', '土木', 'コンピュータ'])
グラフ
import networkx as nx
def init_graph(lst, edge_type='discrete'):
gph = nx.DiGraph()
for idx, x in enumerate(lst):
gph.add_node(idx)
for idx, x in enumerate(lst):
for idy, y in enumerate(lst):
if edge_type == 'discrete':
if y == x:
pass
else:
if wv.similarity(x, y) > 0.5:
gph.add_edge(idx, idy)
return gph
ここでは類似度が0.5以上の単語を似ているものと判断して辺を繋いてグラフを作ります。
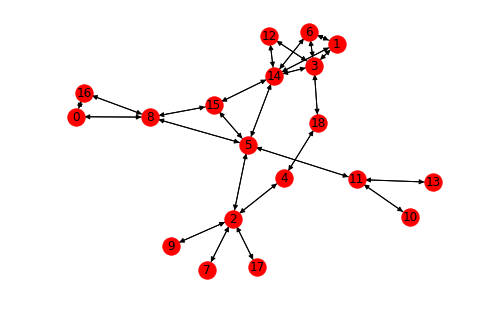
word_graph = init_graph(word_list)
nx.draw(word_graph, with_labels=True)
なんかいい感じのグラフに見えるのは、こうなるように単語を選んたからです(「算盤」から出発して「コンピュータ」に近づくようにランダムに単語を選びました)。一般的にword2vecの単語ベクトルはこのようになっているかどうかはわかりません。
D-Waveで解く
最小被覆問題を解いてみます。
%%time
res = dnx.min_vertex_cover(word_graph, sampler)
print(res)
res_min_vertex_cover = res
[1, 2, 3, 8, 11, 14, 15, 16, 18]
CPU times: user 56.6 ms, sys: 4.51 ms, total: 61.1 ms
Wall time: 2.89 s
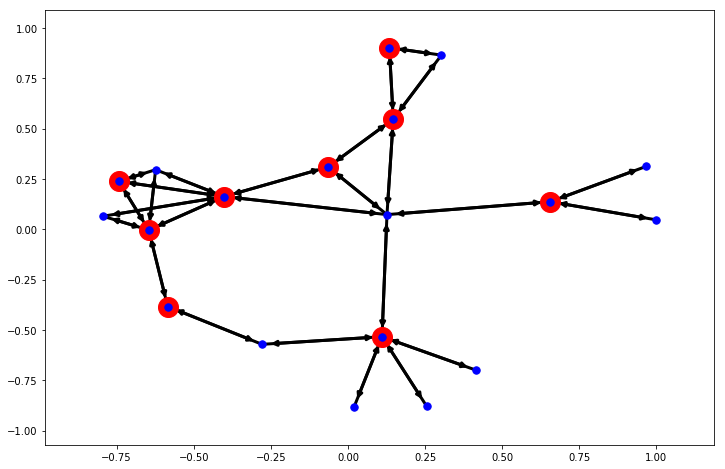
グラフ上ではこんな感じになりました。
node_sele = res_min_vertex_cover
plt.figure(figsize=(12, 8))
pos = nx.spring_layout(word_graph)
nx.draw_networkx_nodes(word_graph, pos, node_size=400, nodelist=node_sele, node_color='r')
nx.draw_networkx_nodes(word_graph, pos, node_size=55, nodelist=range(0, 19), node_color='b')
nx.draw_networkx_edges(word_graph, pos, alpha=1, width=3)
pass
単語にすると次のようになります。
len(res_min_vertex_cover), word_list[res_min_vertex_cover]
(9, array(['理論', '製図', '計算', '算', '手本', '算術', '暗算', '釈', 'コンピュータ'],
dtype='<U6'))
次は最大カット問題です。
%%time
res = dnx.maximum_cut(word_graph, sampler)
print(res)
res_max_cut = res
{0, 1, 2, 3, 4, 8, 11, 14, 15, 17}
CPU times: user 43.9 ms, sys: 3.08 ms, total: 47 ms
Wall time: 2.18 s
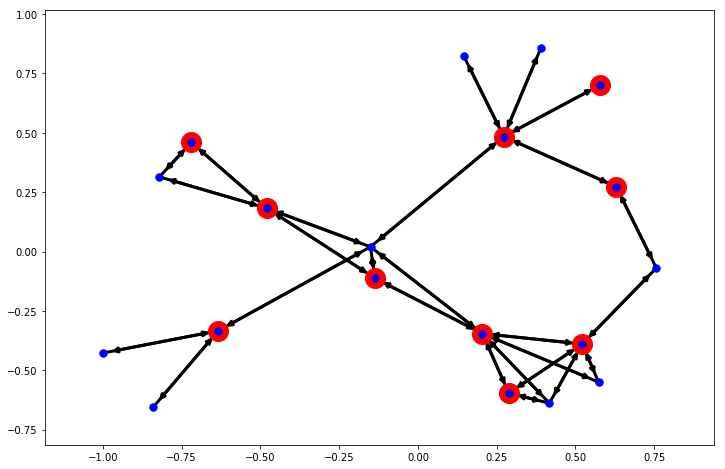
グラフ
node_sele = res_max_cut
plt.figure(figsize=(12, 8))
pos = nx.spring_layout(word_graph)
nx.draw_networkx_nodes(word_graph, pos, node_size=400, nodelist=node_sele, node_color='r')
nx.draw_networkx_nodes(word_graph, pos, node_size=55, nodelist=range(0, 19), node_color='b')
nx.draw_networkx_edges(word_graph, pos, alpha=1, width=3)
pass
うむ。。。右上はちょっと変な気もしますが、この問題は実行するたびに答えが変わりやすい感じがします。正解がいくつある場合はこうなりやすいでしょう。またもっと本質的にはアニーリングマシンが確率的に正しい答えが求まりやすいだけなので、常に正しい答えが返ってくるわけではありません。
単語でみる。
len(res_max_cut), word_list[list(res_max_cut)]
(10, array(['易', '理論', '製図', '計算', 'CAD', '算', '手本', '算術', '暗算', '土木'],
dtype='<U6'))
- 今回は19個程度の単語でグラフを作って問題を解きましたが、この程度ならシミュレータでも実機でも解けます。
- 単語数が30あたりになると、シミュレータではかなり時間がかかって答えが返ってこなくなりました。一方で実機の方は単語50個のグラフでも結果が返ってくることは確認できました。
まとめ
- やったこと:word2vecで言葉グラフを作ってD-waveマシンと遊びました。
- 成果: 結果を眺めて面白がることができました。
- 考察:「だから、ナニ」「それでなにがうれしいの」と問われると、ちょっとつらいところです。
今後の方向としてはこんな感じなものがあるかと思います。
- 今回はテキトーな単語リストを使ったが、もうちょっとマシなセットを工夫する。
- 単語ベクトルどもはクラスタになって高次元空間に疎らに住んでいるようです(例)。全体をクラスタした上でグラフ構造を調べるのが面白い、かも。
- ある文章の中の単語か、何らかの方法で選んだキーワード群に対して解析を行う
- アルゴリズムの工夫をする。
- 最小被覆と最大カット以外にも応用できる問題があるのでそれをやってみる
- 量子・古典ハイブリッドモデルで工夫する
- 自然言語処理のタスク向けに最適化問題を考える。
- あといろいろ…
終わりに
量子デバイスの発展に伴い、量子性を用いて今まで解けなかった問題にアプローチできるかもしれないという期待が膨らんでいる時期です。現在様々なことが提案されていて、今のテクノロジーでは到底無理なものもあれば、本当に近い内に実現して産業応用できるかもしれないものもあって、これから何かをしたいと思っていても進む方向に迷ってしまいます。最後にこちらのD論で見つかった面白い引用を共有したいと思います。
The importance of accelerating approximating and computing mathematics by factors like 10,000 or more, lies not only in that one might thereby do in 10,000 times less time problems which one is now doing...but rather in that one will be able to handle problems which are considered completely unassailable at present.
The projected device, or rather the species of which it is to be the first representative, is so radically new that many of its uses will become clear only after it has been put into operation, and after we have adjusted our mathematical habits and ways of thinking to its existence and possibilities. Furthermore, these uses which are not, or not easily, predictable now, are likely to be the most important ones...because they are farthest removed from what is now feasible.
要約:
計算が桁違いに速くなることの意味は単に同じことをするのに短い時間で済むことではない。今まで手を出すことができなかった問題にアプローチできることの意義の方が遥かに大きい。
そういう新しいデバイスの用途については、現時点で分かる程度のものは些細なものに過ぎないでしょう。我々がこれらのデバイスに慣れ、物事の考え方を合わせられるようになってから初めて、真の使いみちが見えてくるでしょう。
この言葉が発せられたのは、1945年、フォン・ノイマンが手紙に書いたものです。1945年といえばペンシルバニア大学で ENIACが開発されていたころです。コンピュータが生まれたことによって、それまで注目されなかった問題や視点が大きな価値を持つようになったように、量子コンピュータで解けるようになることで初めて意味を持つようになる問題とものの見方が生まれるのではないかと期待しています。