LoginSignup
30
27

More than 3 years have passed since last update.

量子コンピュータAdvent Calendar 2018Day 10
@s_zh

Cirqで動かしながら学ぶ、量子コンピュータ入門

Last updated at Posted at 2018-12-09

この記事では実際にプログラムで動かしながら量子コンピュータの基本的なことについて説明していきます。目指す対象は

  • 量子力学も量子情報も詳しくないけれど、量子コンピュータが速いと言われているが、それはなぜなのか、そして現在どういう問題があって実現できなくて、またこれからどういう発展ができそうか、などについて自分なりの感覚を持つようになるために必要となる基礎を知りたい人
  • 理論物理のバックグランドがあって量子力学はよく知っているけれど量子情報を全然知らないので、ざっくりとした感覚を掴みたい人

の両方です。前半は数学も物理も必要としないように努力しました。後半は量子力学の基本的な枠組がわかることを仮定しています。

notebookはこちら

Cirqについて

Cirqはgoogleから今年の７月に公開した量子コンピュータのフレームワークです。ここによりますとNISQをサポートする、らしい。

量子コンピュータというと素因数分解を古典コンピュータより指数的に早く解くショアのアルゴリズムが有名ですが、最近は量子サポートベクターマシンや量子カーネル法なども提唱されていて夢が広がっております。が、これらのアルゴリズムの多くは一定の精度を得るためにたくさんの量子ゲートが必要で、量子ゲートごとにノイズが重なるため、現在の技術で実用するのが難しいとされています。

そこで、ノイズとうまく付き合ってなんとか近いうちに作れる量子コンピュータで古典コンピュータでは計算できない問題を解いてしまおう、と頑張るのはNISQ（Noisy Intermediate Scale Quantum）です。

NISQで活躍が期待される量子化学計算のOpenFermionをCirq拡張したOpenFermion-Cirqも発表されたり、量子オートエンコーダのサンプルコードが公開されたり、いろいろワクワクする話が出ています。

と、盛り上がったところで、今回はこれらの高度な話に入らず（すいません）、Cirqを動かしながら量子コンピュータがなぜすごいか、ナニが難しいか、の基礎的な部分について解説していきます。

ライブラリのインストールとインポート

こちらに従い、pip install ほにゃららで入るかと思います。注意すべきなのは、Cirqが執筆時点でアルファ版なので、バージョンによってはソースコードが動かないことがあります。こちらで使っているのは0.3.1.35です。

import cirq
import numpy as np
import matplotlib.pyplot as plt

cirq.__version__

'0.3.1.35'

hello qubit

量子コンピュータは０と１の状態を持った量子ビット(quantum bit, qubit)の集まりで計算します。
こんな感じで一個作ってみます。

qubit = cirq.GridQubit(0, 0)

（０，０）の引数は量子ビットを二次元で並べるためにあるものです（NISQなど実際のデバイスを連想してしまいます）。量子コンピュータで計算をするときは量子ビットに様々な操作を加えて全体として一つの回路を作りますが、その一連の操作をcircuitで定義します。最初なので、とりあえずテキトーになんかやって測定する回路を作ってみます。

circuit = cirq.Circuit.from_ops(
    cirq.RotXGate(half_turns=0.2)(qubit),  
    cirq.measure(qubit, key='m')  # Measurement.
)

RotXGateはテキトーなナニかで（ $e^{i\theta \hat{X}}$ みたいなもの）、とりあえずは気にしません。肝心なのは量子コンピュータとはいえ、最後の結果を得るには測定が必要であり、それが最後のcirq.measureです。引数のkeyはなんでもいいみたいです。

print("Circuit:")
print(circuit)

Circuit:
(0, 0): ───X^0.2───M('m')───

回路ができたので、走らせます。

simulator = cirq.google.XmonSimulator()
result = simulator.run(circuit, repetitions=200)

量子力学の世界ではものごとが確率的に決まっているので、結果を知るには何度も測定します。その回数をrepetitionsで渡します。さあ、結果を見てみましょう。

print("Results:")
print(result)

Results:
m=00000000000000010001000000000001000000000000000000000000100000000100000000000000000000000000000001000000000000010001000100010000000000001000000000001000000010000000000000000000000000000100000000000000

ここでは、一個一個の数字が一回一回の測定結果に対応していおり、測定のたびに結果が異なるのが見て取れると思います。実行結果について集計すると次のようになります。

result.histogram(key='m')

Counter({0: 186, 1: 14})]

測定前の量子ビットの状態は、0と１がおおよそ次の比率で入っていることがわかります。

res_count = result.histogram(key='m')
res_count[0]/res_count[1]

13.285714285714286

ついでに理論値も（わからない人は気にしないでください）。

np.tan(0.2*0.5*np.pi)**(-2)

9.472135954999581

qubitを動かす：量子ゲート

量子ビットを操作する手段が様々ありますが、とりあえずアダマールゲートと$\hat{X}$ゲートをみてみます。

アダマールゲート

qubit = cirq.GridQubit(0, 0)
# Create a circuit
circuit = cirq.Circuit.from_ops(
    cirq.H(qubit),  
    cirq.measure(qubit, key='m')  # Measurement.
)

print("Circuit:")
print(circuit)

Circuit:
(0, 0): ───H───M('m')───

実行結果

simulator = cirq.google.XmonSimulator()
result = simulator.run(circuit, repetitions=200)

print("Results:")
print(result)

Results:
m=01110101110000101110100000011101000101110100101010011111011100011110100101100000011011000010001001111110000010101100100100101111110000110011010011000000110010010101110000111110100000101100110011011000

result.histogram(key='m')

アダマールゲートは次のような式で表現されます(式がわからなくても大丈夫です)。
$$
\begin{eqnarray}
\hat{H} \ |0 \rangle = \frac{1}{\sqrt{2}}(|0\rangle + |1\rangle) \\
\hat{H} \ |1 \rangle = \frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)
\end{eqnarray}
$$
肝心なことは

  • アダマールゲートは0の状態も1の状態も0と1が半分ずつ混ざった状態しすること
  • アダマールゲートを二回作用させると、量子ビットの状態が元に戻る 二点です。

次に$\hat{X}$ゲート

qubit = cirq.GridQubit(0, 0)
# Create a circuit
circuit = cirq.Circuit.from_ops(
    cirq.X(qubit),  
    cirq.measure(qubit, key='m')  # Measurement.
)

print("Circuit:")
print(circuit)

Circuit:
(0, 0): ───X───M('m')───

実行結果

simulator = cirq.google.XmonSimulator()
result = simulator.run(circuit, repetitions=200)

print("Results:")
print(result)

Results:
m=11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111

おおよその比率

result.histogram(key='m')

Counter({1: 200})

Xゲートは０と１の状態を入れ替え、二回作用するともとに戻ります。数式で表現する場合は状態ベクトルの定義によっては書き方が異なることがあります。
$$
\begin{eqnarray}
\hat{X} \ |0 \rangle = |1\rangle \\
\hat{X} \ |1 \rangle = |0\rangle
\end{eqnarray}
$$
と書かれる場合もあれば、
$$
\begin{eqnarray}
\hat{X} \ |0 \rangle = -i \ |1\rangle \\
\hat{X} \ |1 \rangle = i \ |0\rangle
\end{eqnarray}
$$
と書かれる場合もあるようです。シミュレーターの方はどちらで実装されているかを確認できます。

qubit = cirq.GridQubit(0, 0)
# Create a circuit
circuit = cirq.Circuit.from_ops(
    cirq.X(qubit),  
#     cirq.X(qubit) 
)

print("Circuit:")
print(circuit)

Circuit:
(0, 0): ───X───

simulator = cirq.google.XmonSimulator()
result = simulator.simulate(circuit)

result.final_state

array([6.123234e-17+0.j, 0.000000e+00-1.j], dtype=complex64)

後者だったようです。

多ビット量子状態と量子優越性

アダマールゲートを作用させるともともと０か１の状態にある量子ビットが０と１が半分ずつ混ざった状態になることを確認しました。この０と１が混ざる状態を扱えることが量子コンピュータの強さの本質です。以下それを具体的に見ていきます。

def get_result_list(result):
    res_hist = result.histogram(key='m')
    res_state = list(res_hist.keys())
    res_state.sort()
    res_list = [[state, res_hist[state]] for state in res_state]
    return np.array(res_list)

n_qubits = 5
n_samples = 5000

qubits = [cirq.GridQubit(i, 0) for i in range(n_qubits)]

circuit = cirq.Circuit()
simulator = cirq.google.XmonSimulator()

circuit.append(cirq.H.on(q) for q in qubits)

circuit.append(cirq.measure(*qubits , key='m'))
result = simulator.run(circuit, repetitions=n_samples)

res_list = get_result_list(result)

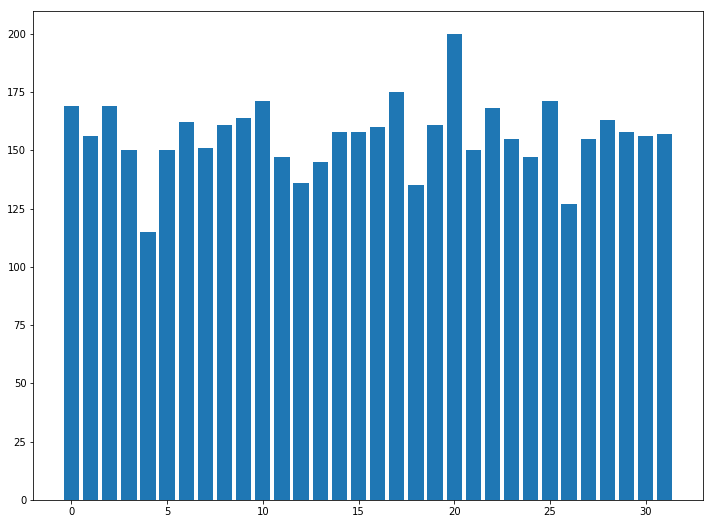
ここで量子ビットを五個用意して、それぞれの量子ビットにアダマールゲートを作用させてから測定してみます。結果は次のようになります。

plt.figure(figsize=(12,9))
plt.bar(res_list[:,0], res_list[:,1])

png

最初は０の状態にある量子ビットにアダマールゲートを作用させるとおのおのの量子ビットが０と１の混合状態になり、全体としては０００００、００００１、０００１１、…、１１１１０、１１１１１のように２の５乗個の状態がすべて同じ重みで重ね合わさった状態になります。これに測定を行うと３２個の状態がほぼ同じぐらいの確率で観測されました。

ここで注目すべきことは今５回の操作(５つのアダマールゲート)しか行っていないのに、$2^5=32$通りの結果が観測されたことです。
古典コンピュータは一度に一つの数字しか表せないが、量子ビットでは重ね合わせを利用していろんな状態を一度に扱うことができます。これを量子並列性といいます。

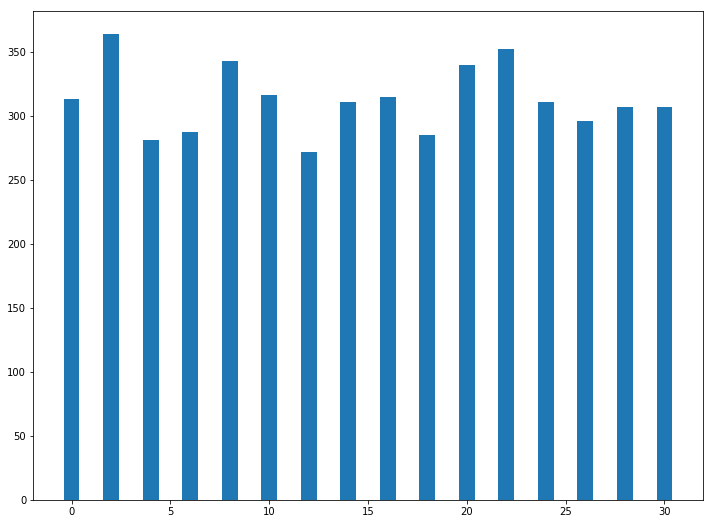
たとえば３２個の状態が均等に実現される量子回路に対して、最初の量子ビットにだけもう一度アダマールゲートを作用させると次のようになります。

n_qubits = 5
n_samples = 5000

qubits = [cirq.GridQubit(i, 0) for i in range(n_qubits)]

circuit = cirq.Circuit()
simulator = cirq.google.XmonSimulator()

circuit.append(cirq.H.on(q) for q in qubits)
circuit.append(cirq.H.on(qubits[-1]))

circuit.append(cirq.measure(*qubits , key='m'))
result = simulator.run(circuit, repetitions=n_samples)

res_list = get_result_list(result)

plt.figure(figsize=(12,9))
plt.bar(res_list[:,0], res_list[:,1])

output_50_1.png

奇数の状態が全部消えて、偶数の状態だけが残りました。アダマールゲートは二度作用するともとに戻ることを考えればこの結果は当たり前にみえるかもしれません。しかし見方を変えると、ここで一度の操作で３２の数字が記録された媒体から奇数をすべて消したことになります。同じことを古典ビットで行おうとすると１６回操作が必要です。

一般的に$n$個の量子ビットを考えると、全体の状態の数は$2^n$になり、古典ビットでは$2^{n-1}$回の操作が必要になるところを量子ビットで一回で済ませることができます。ここに量子コンピュータの可能性を感じます。

もちろん、ここで行った操作がごく簡単なものであり、実際には量子ビット上にある大量の状態を意のままに扱うことができないし、一度にたくさんの状態に対して何らかの操作をしたとしても、最後には観測を通じて結果を得る必要があるため、実際に量子コンピュータを用いてなんらかの現実的な計算を行うにはさまざまな工夫が必要です。また、量子コンピュータがすべての問題に対して強力というわけではありません。次節ではこれらのことを詳しく見ていきますが、まず$2^n$がスゴイことをみていきます。

$45$ビットの量子回路を考えてみましょう。この量子状態を記述するためには$2^{45} \sim　32*10^{12}$の状態の重みを指定する必要があります。古典コンピュータの上でこれを表現する場合、各々の状態の複素数重みをdouble型（８バイト）として全体では$0.5 * 10^{15}$バイト、つまり$0.5$ペタのメモリが必要になります。これはスーパーコンピュータを使ってやっとできるレベルです。そしてさらに４ビット増やして$49$ビットになれば８ペタのメモリが必要なので、スーパーコンピュータでも扱うことが難しくなります（京のメモリが１ペタ余り）。 ちなみに私のmacbook Proで試したところ、$26$ビットはかろうじて動きますが、$27$ビットはフリーズしかけてしまい、ちょっと、慌てました。

このように量子ビット数が５０を超えるあたりから量子回路の中でで起きている現象を従来の古典コンピュータで扱いきれなくなってくるので、ナントなくこのあたりで量子コンピュータをうまく使えば古典コンピュータでは現実的な時間以内（例えば。。。太陽が冷めるまで、とか）で解けないことをやってのけられるかもしれません。それを量子優越性（quantum supremacy）と呼ばれたりしています。こちらの記事をみると、各社の開発がちょうどこのあたりに来ているようです。

量子優越性が目前にあるのもいいですが、それゆえに困ってしまうこともあります。量子コンピュータを作った場合、作ったものが正しく動作することを検証するためには古典コンピュータ上で量子ビットのシミュレーションをする必要があるからです。皮肉ですね。IBMの研究者は量子ビットの状態の情報をハードディスクに避難させ、一部だけをメモリに乗せてシミュレーションしたりしているようです。

４９ビットならメモリに乗らない情報をハードディスクに移すことでシミュレーションができるかもしれませんが、これが３００ビットになるとどうだろう。今度は必要となる重みの数が宇宙にある観測可能の原子の数を超えてしまいますので、情報をハードディスクに記録することさえも不可能になってしまいます。そうなると量子コンピュータの動作確認にはもっと洗練された方法を考える必要が出てきます。

ようするに、５０ビットは結構偉い！３００ビットはもう未知の領域

量子アルゴリズム

ここまでは数式に頼らずに理解できるように努力してきましたが、此処から先は数式を避けては通れないと思います。んで、ここまで読んで頂いたが数式が嫌だという方、御用とお急ぎの方のためにマトメを先に書きます。

  • 量子アルゴリズムはうまい具合にハマると指数的に早くなる（Bernstein-Vaziraniアルゴリズム）
  • ハンパにハマる場合もあって、そのときはハンバに早くなる（groverアルゴリズム）
  • 量子ビット間のコヒーレンスが重要だが、これがノイズに弱い(だから冷やしたりする)
  • 多くのアルゴリズムでは量子ゲートを多数回作用させるので、これもノイズに弱い

-> すぐに何かをしたい場合はNISQでがんばろう

さて、ここからはブラケットの基本的な演算は知っているものと仮定して進めます。

Bernstein-Vaziraniアルゴリズム

量子コンピュータの強さは重ね合わせ状態にあり、たくさんの状態を一度に扱うことができることです。

「じゃあ、とりあえずたくさんの状態をいっぺんに作ってナニかにぶ〜んとなげて、んでこう…なんかこう…うまい具合やれば、スゴイことができそうじゃない？」

と考えてしまうのは自然の流れかと思います。この虫のいい話シンプルなアイディアを具体的な形に落とし込むのはDeutsch-JozsaアルゴリズムやBernstein-Vaziraniアルゴリズムです。

ここではBernsein-Vaziraniの方を説明していきます。

理論

Bernstein-Vaziraniアルゴリズムで解く問題は次の通りです。

今とあるブラックボックスがありました。パラメータ$s_1 \cdots s_n$を持っており、$n$個の入力ビット$x_1\cdots x_n \in {0, 1 }^n $に対して

$$
\begin{eqnarray}
f_s(x) = \sum^{n}_{i=1} s_i x_i \ \ \ (mod \ 2)
\end{eqnarray}
$$

を返します。パラメータ$s_i$を推定せよ。

$f_s(x)$の値は$0$か$1$しか取りません。古典的にこの問題を解く場合、$i$番目のパラメータ$s_i$を知りたければ、$i$番目の入力$x_i$だけが$1$の入力を作ってブラックボックスに入れればいいです。この場合、すべてのパラメータ$s_i$を特定するためにはすべての$x_i$を試す必要があり、$f_s(x)$を$n$回評価することになります。

一方で量子性を利用するとこれが一回で済みます。

アルゴリズムに入る前に、準備として問題のブラックボックスを数式で表現します。次のようになります。
$$
\begin{eqnarray}
U_f \ |x\rangle \otimes |y\rangle　= |x\rangle \otimes |f_s(x) \oplus y\rangle
\end{eqnarray}
$$
$U_f$はオラクル（神託）と呼ばれ、入力$x_i$に対し、結果$f_s(x_i)$の値を補助ビット（ancilla、$|y\rangle$）を通してわれわれに伝えるイメージです。$f_s(x) \oplus y$は排他的論理和で、$f_s(x)$と$y$の片方が$0$、もう片方が$1$のときにのみ$1$の値を取り、それ以外の場合は$0$の値を取ります。入力値$x_i$に対する出力$f_s(x)$を得るときにブラックボックスに問い合わせる行為は状態$|x\rangle$に対して$U_f$を作用させることに対応します。量子力学の線形性から、いったん個々の$|x\rangle$に対して$U_f$が与えられれば、問い合わせに使う状態をさまざまな$\sum_{x'} |x'\rangle$の重ね合わせ状態を使うことができます。そこで一度の問い合わせで様々な$|x\rangle$に対する答えがエンコーディングされた状態を得ることができます。ただし、その答えがエンコーディングされた状態からほしい答えを引き出すのが一般的に容易ではなく、今の問題に対しては知りたい情報をうまく取り出す方法が見つかっていて、それがBernstein-Vaziraniアルゴリズムです。

Bernstein-Vaziraniアルゴリズムは次の通りです。
1. $1$から$n$番目の量子ビット（入力ビット）にアダマールゲートを作用させ、$n+1$番目の量子ビット（補助ビット）には$X$ゲートを作用させてからアダマールゲートを作用させます。
2. オラクルに問い合わせます（$U_f$を作用させます）。
3. $1$から$n$番目の量子ビット（入力ビット）に再びアダマールゲートを作用させます。
4. $1$から$n$番目の量子ビット（入力ビット）を観測して、それぞれの値が$s_i$に対応します。

最初にすべてのビットは$|0\rangle$の状態にあり、$X$ゲートは$|0\rangle$を$|1\rangle$に変えるので、ステップ１のあとで量子ビットの状態が次のようになります。
$$
\begin{eqnarray}
|0\rangle^{\otimes n+1}
\rightarrow
\frac{(|0\rangle + |1\rangle)^{\otimes n}}{\sqrt{2^{n}}} \otimes
\frac{|0\rangle - |1\rangle}{\sqrt{2}}
= \frac{1}{\sqrt{N}} \sum_{x=0}^{2^n-1} |x\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}}
\end{eqnarray}
$$

ステップ２でオラクル$U_f$を作用させると次のようになります。
$$
\begin{eqnarray}
\frac{1}{\sqrt{N}} \sum_{x}^{2^n-1} |x\rangle \otimes \frac{|f_s(x)\oplus 0\rangle - |f_s(x) \oplus 1\rangle}{\sqrt{2}}
= \frac{1}{\sqrt{N}} \sum_{x=0}^{2^n-1} (-1)^{f_s(x)} |x\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}}
\end{eqnarray}
$$
イコールでは$|f_s(x)\oplus 0\rangle - |f_s(x) \oplus 1\rangle=(-1)^{f_s(x)}(|0\rangle - |1\rangle)$を使いました。$f_s(x)$が$0$と$1$の場合を代入すると簡単に確認できます

ステップ３で$|x\rangle$の重ね合わせ状態にアダマールゲートを作用させると$|s\rangle$に変わります。
$$
\begin{eqnarray}
\frac{1}{\sqrt{N}} \sum^{2^n - 1}_{x=0}(-1)^{f_s(x)} H^{\otimes n} |x\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}}
= |s\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}}
\end{eqnarray}
$$

上の式を導出するには$(-1)^{f_s(x)}|x\rangle = \prod_{i=1}^n (-1)^{s_i x_i} |x_i\rangle$に注意して、$\frac{1}{\sqrt{N}} \sum_x (-1)^{f_s(x)} |x\rangle = \prod_i^n \frac{|0\rangle + (-1)^{s_i}|1\rangle}{\sqrt{2}}= \prod_i^n \frac{H|s_i\rangle}{\sqrt{2}}$となるので、最後に$HH=1$を使えばいいです。

最後にステップ４でビットの値を観測すれば$s_i$が求められます。

実装

では、Bernstein-Vaziraniアルゴリズムを実装していきます。今まで見てきたように、実装…とオオゲサに言っても、$X$ゲートとアダマールゲートを作用させるだけですね。

入力ビット数を与えて、入力ビットと補助ビットを作ります。

def init_circuit(qubit_count):
    circuit = cirq.Circuit()
    input_qubits = [cirq.GridQubit(i, 0) for i in range(qubit_count)]
    ancilla_qubit = cirq.GridQubit(qubit_count, 0)
    return circuit, input_qubits, ancilla_qubit

ステップ１、補助ビット（ancilla_qubit）に$X$ゲートを作用させてからアダマールゲート、入力ビットにはアダマールゲートだけを作用させます。

def step1(circuit, input_qubits, ancilla_qubit):
    circuit.append([
        cirq.X(ancilla_qubit),
        cirq.H(ancilla_qubit),
        cirq.H.on_each(input_qubits),
    ])
    return circuit

次にオラクルを作用…させたいですが、これはちょっとめんどう自明じゃない…ので一旦置いておいて、あとでやります。このアルゴリズムの本質はオラクルが既存(与えられたもの)として、それをどう推定するかです(つまり誰かが持ってきたブラックボックスの中身を調べるのが仕事)。オラクルの実装そのものが本質ではありません。

# 一旦飛ばす
def step2(circuit, input_qubits, ancilla_qubit):
    return circuit

そして、ステップ３はまたアダマールゲートを作用させるだけですが、もうステップ４の測定も一緒にやってしまいましょう

def step3to4(circuit, input_qubits, ancilla_qubit):
    circuit.append([
        cirq.H.on_each(input_qubits),
        cirq.measure(*input_qubits, key='result')
    ])
    return circuit

これで関数ができたので、あとは呼び出して実行ですね。

circuit_sample_count = 3
n_qubits = 8

circuit, input_qubits, ancilla_qubit = init_circuit(n_qubits)
circuit = step1(circuit, input_qubits, ancilla_qubit)
circuit = step2(circuit, input_qubits, ancilla_qubit)
circuit = step3to4(circuit, input_qubits, ancilla_qubit)

def bitstring(bits):
    return ''.join(str(int(b)) for b in bits)

simulator = cirq.google.XmonSimulator()
result = simulator.run(circuit, repetitions=circuit_sample_count)
frequencies = result.histogram(key='result', fold_func=bitstring)
print('Sampled results:\n{}'.format(frequencies))

Sampled results:
Counter({'00000000': 3})

オラクルが実装されていないので、こうなりました。何もしないオラクルでは補助ビットが常にそのままで、すべての$s_i$が$0$の状況に対応するので、出力もすべて０になります。

オラクル

本質ではない部分なので時間をかけることにあまり気乗りしないですが、これをやらないと実行して何かを確認することもできません。なのでオラクルを実装しましょう（量子ゲートを理解するのにいい練習だと思います）。オラクルの定義は

$$
\begin{eqnarray}
U_f \ |x\rangle \otimes |y\rangle　= |x\rangle \otimes |f_s(x) \oplus y\rangle
\end{eqnarray}
$$

入力ビット$|x\rangle$の値に応じて補助ビット$|y\rangle$の値を変えるので、これを実現するには各々のビット$|x_i\rangle$に応じて補助ビットを変えるゲートが必要になります。CNOT（Controlled NOT）ゲートを使います。

$$
\begin{eqnarray}
\hat{C}_{NOT} |x\rangle \otimes |y\rangle = |x\rangle \otimes |x \oplus y \rangle
\end{eqnarray}
$$

この作用は$|x\rangle$の値によって$|y\rangle$の値を変えるので、初見だと違和感を覚えるかもしれません。CNOTは決して$|x\rangle$を測定してから$|y\rangle$を操作するものではなく、単にこういうタイプの相互作用です。「CNOT implementation」で検索すればさまざまな実現方法が出てきます。また、実際に行列表現に書き起こせばユニタリ性をチェックすることもできます。

$$
\begin{eqnarray}
C_{NOT} = \left(
\begin{array}{cccc}
1 & 0 & 0 & 0\\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1\\
0 & 0 & 1 & 0
\end{array}
\right)
\end{eqnarray}
$$

ただし、ここではベクトルの成分は$|00\rangle, |01\rangle, |10\rangle, |11\rangle$となっています。

CNOTを使ってオラクルを実装しましょう。定義$a \oplus b = a+b \ (mod \ 2)$と結合則を使うと
$$
\begin{eqnarray}
\sum_{i} s_i x_i \oplus y
= \sum_{i} s_i x_i + y \ (mod \ 2)
= \sum_{i \ for \ s_i=1} x_i + y \ (mod \ 2)
= \sum_{\oplus \ with \ i \ for \ s_i=1}^{} x_i \oplus y
\end{eqnarray}
$$

となるので、$s_i$が$1$の$i$に対して$i$番目の入力ビットと補助ビットに作用するCNOTゲートを構成すればいいことになります。実装は次のようになります。

def make_oracle(circuit, input_qubits, ancilla_qubit, secret_bits):

    for qubit, bit in zip(input_qubits, secret_bits):
        if bit:
            circuit.append([cirq.CNOT(qubit, ancilla_qubit)])
    return circuit

オラクルができたので、動かしてBernstein-Vaziraniアルゴリズムを確認することができます。

circuit_sample_count = 3
n_qubits = 8

# パラメータs_iをランダムに生成する
secret_bits = np.random.randint(2, size=8)
circuit, input_qubits, ancilla_qubit = init_circuit(n_qubits)
circuit = step1(circuit, input_qubits, ancilla_qubit)
circuit = make_oracle(circuit, input_qubits, ancilla_qubit, secret_bits)
circuit = step3to4(circuit, input_qubits, ancilla_qubit)

def bitstring(bits):
    return ''.join(str(int(b)) for b in bits)

simulator = cirq.google.XmonSimulator()
result = simulator.run(circuit, repetitions=circuit_sample_count)
frequencies = result.histogram(key='result', fold_func=bitstring)
print('Sampled results:\n{}'.format(frequencies))

Sampled results:
Counter({'01100011': 3})

出力が得られたので、もとの$s_i$を確認してみます。

secret_bits

array([0, 1, 1, 0, 0, 0, 1, 1])

いっちしました。

考察

Bernstein-Vaziraniアルゴリズムは量子コンピュータの仕組みを説明するのに適していますが、実用的ではありません。

重要なポイントは量子ビット$x$に対して関数$f(x)$の働きをする操作（オラクル）が存在すれば、非常に低コスト(N個の状態を$\log{N}$回の操作)ですべての状態を作っていっぺんに試すことができることです。

そうするとあとは解きたい問題のオラクルを作れば、もういろんなことを試せそうな気がしてきますね。しかし理論の部分でも見た通り、このケースではたまたまアダマールゲートを使って目的の情報$s_i$を出力ビットに反映させて取り出すことができたので従来のコンピュータに対して指数的に速い計算スピードを得ることができました。一般的にこれがうまくいかないケースも多いです。次にみるgroverアルゴリズムのように、問題によっては目的の情報を出力ビットに反映させることが難しい場合もあり、この場合量子コンピュータを使うことによって得られる恩恵小さくなります（指数的には速くならず、ルートで速くなります）。

grover アルゴリズム

解く問題：
$f(x)$という関数があって、$x_0$に対してだけ$f(x_0)=1$でそれ以外の$x$では$f(x)=0$となります。$x_0$を求めよう。

groverアルゴリズムは「検索のアルゴリズム」として紹介されることが多いですが、元論文の書き方もあってか、データベースの検索タスクを連想させてしまいますが、実際には「解の検索」問題として捉えたほうが適切です。$f(x)$の働きをするオラクル$U_f$が与えられたとして、$x_0$を探す問題になります。

この問題もBernstein-Vaziraniアルゴリズム同様、古典コンピュータではしらみつぶしに$x_0$を一つずつ試すしかないので、$x$の取りうる数を$N$個だとして最悪$N$回探さなければ答えが見つかりません。量子性を利用すると低いコストですべての$x$状態をいっぺんにオラクルに問い合わせることができるので、古典コンピュータより速く（少ない手順で）答えにたどり着きます。しかしBernstein-Vaziraniアルゴリズムの場合と違って、この場合、答えを引き出すのが簡単ではありません。

補助ビットと入力ビットを使って、
1. 入力ビットにアダマールゲートを作用させ、補助ビットに$X$ゲートを作用させてからアダマールゲートを作用させます。
2. オラクルに問い合わせます（$U_f$を作用させます）。

を行うと、次のようになります。

$$
\begin{eqnarray}
\frac{1}{\sqrt{N}} \sum_{x=0}^{2^n-1} (-1)^{f_s(x)} |x\rangle \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}}
= \frac{1}{\sqrt{N}} \left(-|x_0\rangle + \sum_{x\neq x_0} |x\rangle \right) \otimes \frac{|0\rangle - |1\rangle}{\sqrt{2}}
\end{eqnarray}
$$

この場合ターゲットとなる$|x_0\rangle$だけ確率振幅がマイナスになっていますが、この状態では確率$\frac{1}{\sqrt{N}}$でしか$|x_0\rangle$を観測できないので、メリットがありません。確率振幅の符号がマイナスになっていることを利用して$|x_0\rangle$の確率を増幅するのがgroverアルゴリズムです。

確率振幅増幅

まず次のように書き換えます。

$$
\begin{eqnarray}
\frac{1}{\sqrt{N}}
\left(-|x_0\rangle + \sum_{x\neq x_0} |x\rangle \right)
= \frac{1}{\sqrt{N}}
\left(-2|x_0\rangle + \sum_{x} |x\rangle\right)
\end{eqnarray}
$$

$\sum_x |x\rangle$の部分は入力ビットにアダマールゲートを作用させることで生成されるので、入力ビットに再びアダマールゲートを作用させると$|0\rangle$に戻ります。一方で$|x_0\rangle$の部分はアダマールゲートを作用させるとさまざまな$|x\rangle$の重ね合わせ状態になります。この状態で$|0\rangle$だけを$-|0\rangle$と確率振幅の符号をひっくり返して、それ以外の状態をそのままになるように操作し、そして再びすべてのアダマールゲートを作用させることを考えよう、$|0\rangle$は元の$\sum_x |x\rangle$に戻りますが、それ以外の$|x\rangle$の重ね合わせ部分を$|x_0\rangle$へ戻すには$\frac{2}{N}|0\rangle$だけ足りないはずです。
この分を補い、残りを変換前の$|0\rangle$で吸収することを考えると、変換後の$\sum_x |x\rangle$の振幅はそれだけ小さくなり、$\frac{1-4/N}{\sqrt{N}}$となっているはずです。
そして確率の保存を考えると最終的に$|x_0\rangle$の振幅が$\frac{3-4/N}{\sqrt{N}}$と変換前より増幅されたことになります。

数式で求めると次のようになります。まず入力ビットすべてにアダマールゲートを作用させる

$$
\begin{eqnarray}
\rightarrow - \frac{2}{N}\sum_{x'}　(-1)^{\langle x', x_0\rangle}|x'\rangle + |0\rangle
\end{eqnarray}
$$

$|０\rangle$だけひっくり返して、他の成分をそのままにする（実現方法については次節で）

$$
\begin{eqnarray}
\rightarrow
- \frac{2}{N}\sum_{x'\neq 0} (-1)^{\langle x', x_0\rangle }|x'\rangle - (1-2/N)|0\rangle
= - \frac{2}{N} \sum_{x'} (-1)^{\langle x', x_0\rangle} |x' \rangle - (1-4/N)|0\rangle
\end{eqnarray}
$$

再びすべての入力ビットにアダマールゲートを作用させる

$$
\begin{eqnarray}
\rightarrow
\frac{1}{\sqrt{N}}
\left(-2|x_0\rangle
- (1-4/N) \sum_{x} |x\rangle\right)
= \frac{1}{\sqrt{N}}
\left(-(3-1/N)|x_0\rangle
- (1-4/N) \sum_{x \neq x_0} |x\rangle\right)
\end{eqnarray}
$$

という計算になります。増幅したあとに$|x_0\rangle$の符号がほかの$|x\rangle$と揃ったので、再び$|x_0\rangle$を増幅させるにはもう一度オラクルを作用させる必要があります。オラクルと増幅を繰り返していけば最終的に$|x_0\rangle$が高い確率で観測されるように持っていくことができます。一度繰り返すたびに$|x_0\rangle$の増幅幅はおおよそ$\frac{2}{\sqrt{N}}$のオーダーなので、これを大きな値にするには大体$\sqrt{N}$回繰り返す必要があります。ゆえにgroverアルゴリズムでは指数的にではなく$\sqrt{N}$程度に速くなります。それでも$N$が１億程度なら10000倍速くなるので、夢が小さくなりますが、実現されれば十分価値あるものです。

制御ゲート

確率振幅を増幅する際に$|0\rangle$の符号だけをひっくり返して他の状態をそのままにする操作を仮定しました。この操作はCNOTゲートの拡張を考えると実現できます。つまり複数の入力ゲートの値がすべて$1$の場合にのみ補助ゲートの値を変えようにすればいいです。具体的な実現方法は自明ではありませんが、「Multiple-Controlled gate」で検索するといろいろ論文が出てきます。すべてのビットの値が揃ったときにのみ動作するものを作るには、二回作用させれば元にもどるゲートをMultiple-Controlledゲートの両辺で挟み、補助ビットにNOTゲートがかかるときに符号が変わるようにすればいいです。$|0\rangle$のときに反応させたいのですべてのビットにXゲートを作用させます、そして補助ビットの符号をひっくり返すためにはアダマールゲートを使えばできます。

考察

groverアルゴリズムの考え方がさまざまな研究に応用されていますが、実際のマシンで使うには$\sqrt{N}$回もゲート操作を繰り返す必要があるため、現在の技術で実現するのが難しそうです。これはgroverアルゴリズムに限らず、多くのアルゴリズムでは量子ゲートを多くの回数作用させることが必要になります。そのたびにノイズが加算されるので有意な結果を得ることが難しいのが現状です。

それを乗り越えるためにさまざまな方法が提案されています。その中でも量子計算と古典計算を組み合わせて問題を解いていくアプローチが近い将来力を発揮するかもしれません。

参考文献

  • 教科書
    • 現代量子物理学―基礎と応用：量子力学の教科書です。量子情報に一章を割いています。本質をわかりやすく説明してくれています。
    • 量子情報科学入門：基本的なアルゴリズムを丁寧に導出してくれるだけでなく、考え方についても述べています。
  • 論文
  • その他資料
    • Qiskit Tutorial: 基本的なことから最近の論文まで、幅広く面白いjupyter notebookがたくさんあって、漁るの楽し(私のお気に入りはこちらの量子絵文字、笑えるので、ぜひ！ちなみに量子機械学習関連もあります)
    • Blueqat Tutorial:日本語のチュートリアルノートブックです。どれも良質で、数自体も増えているようです。
    • アニーリング系：本文では触れませんでしたが、現状では量子ゲートマシンよりもアニーリングマシンのほうが一歩先を行っている感じがします。こちらの資料です。
      • Wildqat example: 日本語のjupyter notebookが豊富です。「最適化問題」とだけ言われてもピンと来ませんが、これを読めば、本当にいろんなことができそうだということがわかります。MDR社に感謝。
      • D-Wave Leap: D-Wave社の入門サイト、動画もあってわかりやすい。内容いろいろあって楽しいです。
      • 量子コンピュータの現状と未来:　量子アニーリングの生みの親である西森先生の講演資料です。わかりやすい（関係ないことですが、西森先生といえばわたくしなどはこちらのシュレ-ディンが音頭を真っ先に思い浮かびますが、ご兄弟らしいです）
30
27
1

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
30
27