目的
随時更新されているKPIの時系列データに関して、数値に異常があった場合になるべく早くアラートを出せるようにしたいという要請がありました。これはいわゆる異常検知の問題です。多くの場合、異常検知では異常・正常を判定するラベル情報がないので、教師あり学習ができないことが多いです。教師なしで時系列データを異常検知する方法としては、ARIMA など時系列モデルを当てはめて、予測値と実績値の差が大きすぎるものを異常判定する、という方法が考えられます。しかし、この方法は精度の高い時系列モデルを作成できることが前提です。そこで、別のアプローチがないか調べたところ、参考文献 [3] で特異スペクトル変換 (SST, 別名: SSA, 特異スペクトル分析)という方法を見つけたので試すことにしました。
特異スペクトル変換には、
- 時系列データの分布の形状に依存せず、さまざまな形状に対応できる
- 仕組みが比較的簡単 (よって処理に時間がかからない)
という利点があるとのことです。
特異スペクトル変換の説明
特異スペクトル変換では、分布を仮定できないため、時系列データからなんらかの「時系列の特徴」を表す成分を取り出した上で成分を比較し、どの程度差異があるかを異常度合いにします
- 時系列からある長さ ($w$) だけ部分時系列を抜き出します。${x_1, x_2, \cdots, x_{T}}$ という時系列データがあるとすると、適当なところから $[x_t, x_{t+1}, \cdots, x_{t+w-1}]$ を取り出します。これを $\boldsymbol{y}_{t}$ とします。
- 1期間だけ後にずらして、同様に $w$ だけ取り出すということを、$M-1$回繰り返します。つまり、$$\begin{gather}
\begin{bmatrix}x_1 & \cdots & x_{t-1} &\underset{\boldsymbol{y}_{t}}{\underbrace{\begin{bmatrix}x_{t} & x_{t+1} & \cdots & x_{t+w-1}\end{bmatrix}}} & x_{t+w} & \cdots & x_{T}\end{bmatrix}\
\begin{bmatrix}x_{1} & \cdots & x_{t} & \underset{\boldsymbol{y}_{t+1}}{\underbrace{\begin{bmatrix}x_{t+1} & x_{t+2} & \cdots & x_{t+w}\end{bmatrix}}} & x_{t+w+1} & \cdots & x_{T}\end{bmatrix}\
\vdots \
\begin{bmatrix}x_1 & \cdots & x_{t+M-2} & \underset{\boldsymbol{y}_{t+M-1}}{\underbrace{\begin{bmatrix}x_{t+M-1} & x_{t+M} & \cdots & x_{t+(M-1)+(w-1)}\end{bmatrix}}} &
x_{t+(M-1)+w} & \cdots & x_T\end{bmatrix}\
\end{gather}$$
という風に取り出していきます。 これは後述のプログラムのwindow()関数の処理に対応しています。 - これらの部分時系列を列ベクトルとみなして、順にならべた行列 $$
\begin{align}
\mathbf{H}_{t}:&=\begin{bmatrix}\boldsymbol{y}_{t} & \boldsymbol{y}_{t+1} & \cdots & \boldsymbol{y}_{t+M-1}\end{bmatrix}\
&=\begin{bmatrix}\begin{bmatrix}x_{t}\
x_{t+1}\
\vdots\
x_{t+w-1}
\end{bmatrix} & \begin{bmatrix}x_{t+1}\
x_{t+2}\
\vdots\
x_{t+w}
\end{bmatrix} & \cdots & \begin{bmatrix}x_{t+M-1}\
x_{t+M}\
\vdots\
x_{t+M-1+w-1}
\end{bmatrix}\end{bmatrix}
\end{align}$$
を考えます。 $\mathbf{H}_t$ はハンケル行列であると紹介する文献もありますが、ハンケル行列はふつう正方行列のことを言います。特異スペクトル変換は正方行列でなくても可能です。つまり、部分時系列の長さ $w$ とラグの数 $M$ が同じでなくても計算できます。
この $\mathbf{H}_t$ に対して、特異値分解 (SVD) という操作をします。SSA_anom()関数がこの処理に対応しています。
なお、今回紹介する異常検知の方法を特異スペクトル変換と呼ぶのは考案者である井出らによるもので、一般に特異スペクトル変換というと、以上の部分時系列の行列 $\mathbf{H}_t$ を特異値分解する処理のことだけを言うことが多いです。(特に英語で検索すると、こちらのほうが多くヒットします)
特異値分解とは
行列を分解し、特異値と特異ベクトルと呼ばれるものを、元の行列の特徴を表すものとして取り出せる。ある行列 $\mathbf{A}$ を、$
\begin{align}
\mathbf{A} &= \mathbf{U}\boldsymbol{\Sigma}\mathbf{V}
\end{align}$と言うかたちで表します。$\mathbf{U}, \mathbf{V}$ はそれぞれ、左特異行列、右特異行列といいます。 $\boldsymbol{\Sigma}$ は正方行列ではありませんが、正方行列になるよう左側から部分行列を取り出したものは、対角行列になります。この対角成分を上から順に「第n特異値」という風に表します。$\mathbf{U}$ の列ベクトルも、コレに対応する形で左から順に「第n左特異ベクトル」というふうに呼びます。
対角化と似ていますが、$\mathbf{A}$ がどのような成分でも、正方行列でなくてもこの形にできます。もう少し細かいことを言うと、 $\mathbf{A}$ を特異値分解して得られる対角行列 $\boldsymbol{\Sigma}$ は、 $\mathbf{A}^\top\mathbf{A}$ を対角化した対角行列の平方根です。具体的な計算方法は、他の文献を参照してください。
実は、主成分分析 (PCA) と特異値分解は数学的に同じ操作をしています。次元ごとの分散が大きくなるようにベクトル空間の基底を取り直して、その分散の大きさを主成分スコアとし、各成分を主成分負荷量としています。これは、特異値分解の特異値と特異ベクトルにそれぞれ対応します。変換後は特異値の大きい次元ほど、データのばらつきをよく捉えているので、特異値の小さい次元は重要度が低いとみなして除去します。主成分分析と同じと考えると、 $\mathbf{H}_t$ の特異値分解は、時系列の持つ情報の次元削減をしていると言えます。Python では、特異値分解は numpy.linalg.svd() で計算できるため、今回もこれを使用しています。
特異スペクトル変換による異常度の定義
では、特異値分解からどのように異常度を定義するかを説明します。
- 上記の方法で $t$ 時点で部分を切り取って、行列 $\mathbf{H}_t$ (これをテスト行列と呼びます) を構成し、2つ目は遡って $t - L$ 時点で切り取り、 $\mathbf{H}_{t-L}$ (これを履歴行列と呼びます) を構成します。
- テスト行列と履歴行列について、特異値分解し、それぞれの左特異ベクトルを順にならべた行列$\mathbf{Q},\mathbf{U}$を求めます。特異ベクトルはすべてではなく、対応する特異値の大きい順に一部だけ取り出しても構いません。
- 2つの特異ベクトルの組から、2箇所で変化の仕方がどれくらい違うかの度合い、つまり「異常度」を計算する。
- 切り取る場所をすこしづつスライドさせることで、異常度の時系列データを作成できます。
- ようは2つの行列の比較なので、問題によっては履歴行列だけ取り出す時期を固定するという方法でも可能だと思います。
- 参考文献[3]の提案した方法では、
$$
\begin{align}
a_t &= 1 - {|\mathbf{U}^\top\mathbf{Q}|}_2
\end{align}
$$
という式で異常度 $a_t$ を計算します。こう定義すると、 $a_t$ は 0と1の間をとり、2つの時系列が全く異なるなら1、全く同じならゼロになります。実際には、行列ノルム $|\mathbf{U}^\top\mathbf{Q}|_2$ は、 $\mathbf{U}^\top\mathbf{Q}$ の第1特異値と等しくなるので、そちらを計算します。
以下が python (jupyter) で書いたプログラムです。
%matplotlib inline
import matplotlib
import matplotlib.pyplot as plt
import numpy as np
import scipy as sp
import pandas as pd
from itertools import islice
plt.style.use('seaborn-whitegrid')
# SSA 用の関数
def window(seq, n):
"""
window 関数で要素を1づつずらした2次元配列を出す. 戻り値は generator
"""
"Returns a sliding window (of width n) over data from the iterable"
" s -> (s0,s1,...s[n-1]), (s1,s2,...,sn), ... "
it = iter(seq)
result = tuple(islice(it, n))
if len(result) == n:
yield result
for elem in it:
result = result[1:] + (elem,)
yield result
def SSA_anom(test, traject, w, ncol_t, ncol_h, ns_t, ns_h,
normalize=False):
"""
特異スペクトル分析 (SSA) による時系列の特徴づけ
ARGUMENTS:
-------------------------------------------------
test: array-like. テスト行列を作る部分時系列
tracject: array-like. 履歴行列を作る部分時系列
ns_h: 履歴行列から取り出す特異ベクトルの数
ns_t: テスト行列から取り出す特異ベクトルの数
-------------------------------------------------
RETURNS:
3要素のタプル:
要素1: 2つの部分時系列を比較して求めた異常度
要素2, 3: テスト行列・履歴行列をそれぞれの特異値の累積寄与率
"""
H_test = np.array(
tuple(x[:ncol_t] for x in window(test, w))[:w]
) # test matrix
H_hist = np.array(
tuple(x[:ncol_h] for x in window(traject, w))[:w]
) # trajectory matrix
if normalize:
H_test = (H_test - H_test.mean(axis=0,
keepdims=True)) / H_test.std(axis=0)
H_hist = (H_hist - H_hist.mean(axis=0,
keepdims=True)) / H_hist.std(axis=0)
Q, s1 = np.linalg.svd(H_test)[0:2]
Q = Q[:, 0:ns_t]
ratio_t = sum(s1[0:ns_t]) / sum(s1)
U, s2 = np.linalg.svd(H_hist)[0:2]
U = U[:, 0:ns_h]
ratio_h = sum(s2[0:ns_t]) /sum(s2)
anom = 1 - np.linalg.svd(np.matmul(U.T, Q),
compute_uv=False
)[0]
return (anom, ratio_t, ratio_h)
def SSA_CD(series, w, lag,
ncol_h=None, ncol_t=None,
ns_h=None, ns_t=None,
standardize=False, normalize=False, fill=True):
"""
Change Detection by Singular Spectrum Analysis
SSA を使った変化点検知
-------------------------------------------------
w : window width (= row width of matrices) 短いほうが感度高くなる
lag : default=round(w / 4) Lag among 2 matrices 長いほうが感度高くなる
ncol_h: 履歴行列の列数
ncol_t: テスト行列の列数
ns_h: 履歴行列から取り出す特異ベクトルの数. default=1 少ないほうが感度高くなる
ns_t: テスト行列から取り出す特異ベクトルの数. default=1 少ないほうが感度高くなる
standardize: 変換後の異常度の時系列を積分面積1で規格化するか
fill: 戻り値の要素数を NaN 埋めで series と揃えるかどうか
-------------------------------------------------
Returns
list: 3要素のリスト
要素1: 2つの部分時系列を比較して求めた異常度のリスト
要素2, 3: テスト行列・履歴行列をそれぞれの特異値の累積寄与率のリスト
"""
if ncol_h is None:
ncol_h = round(w / 2)
if ncol_t is None:
ncol_t = round(w / 2)
if ns_h is None:
ns_h = np.min([1, ncol_h])
if ns_t is None:
ns_t = np.min([1, ncol_t])
if min(ncol_h, ncol_t) > w:
print('ncol and ncol must be <= w')
if ns_h > ncol_h or ns_t > ncol_t:
print('I recommend to set ns_h >= ncol_h and ns_t >= ncol_t')
start_at = lag + w + ncol_h
end_at = len(series) + 1
res = []
for t in range(start_at, end_at):
res = res + [SSA_anom(series[t - w - ncol_t:t],
series[t - lag - w - ncol_h:t - lag],
w=w, ncol_t=ncol_t, ncol_h=ncol_h,
ns_t=ns_t, ns_h=ns_h,
normalize=normalize)]
anom = [round(x, 14) for x, r1, r2 in res]
ratio_t = [r1 for x, r1, r2 in res]
ratio_h = [r2 for x, r1, r2 in res]
if fill == True:
anom = [np.nan] * (start_at - 1) + anom
if standardize:
c = np.nansum(anom)
if c != 0:
anom = [x / c for x in anom]
return [anom, ratio_t, ratio_h]
補足説明
実はこの処理は、参考記事 [2]で紹介されてるR言語を用いた実装と、やっていることがほぼ同じです。唯一の違いは、参考記事は、1から第1特異値の2乗を引いたものを異常度としていますが、ここでは2乗していません。前者の定義は[1]で紹介されているもので、部分空間どうしの2乗距離です。後者の異常度は、参考文献[3]の定義に従っています。これらはいずれもゼロと1の間におさまるため、異常度の定義として自然です。
今回は、$\mathbf{H}_t, \mathbf{H}_{t-L}$ の標準化 (平均ゼロ、分散1になるように調整すること) を行えるオプションも追加しています。これは、特異値分解と数学的に等価である主成分分析は、スケールの違いを考慮していないため、前処理として標準化を行うのが一般的だからというのが理由です。ただし、標準化を行うと、振れ幅だけが変化した時系列や、切片が上下どちらかに移動しただけの時系列が、全て同じものとして扱われてしまいます。そのため、連続的に変化を監視し続けなければ、変化を見落とす可能性があります。そもそも、時系列をスライドしてスケールが変わるような状況じたいが一種の異常状態とみなすべきという場合がほとんどだと思いますので、標準化する必要に迫られる場面は少ないと思いますが、タスクの要件定義しだいでは前処理を工夫すればいろいろな問題に対処できるということで紹介しました。
テスト
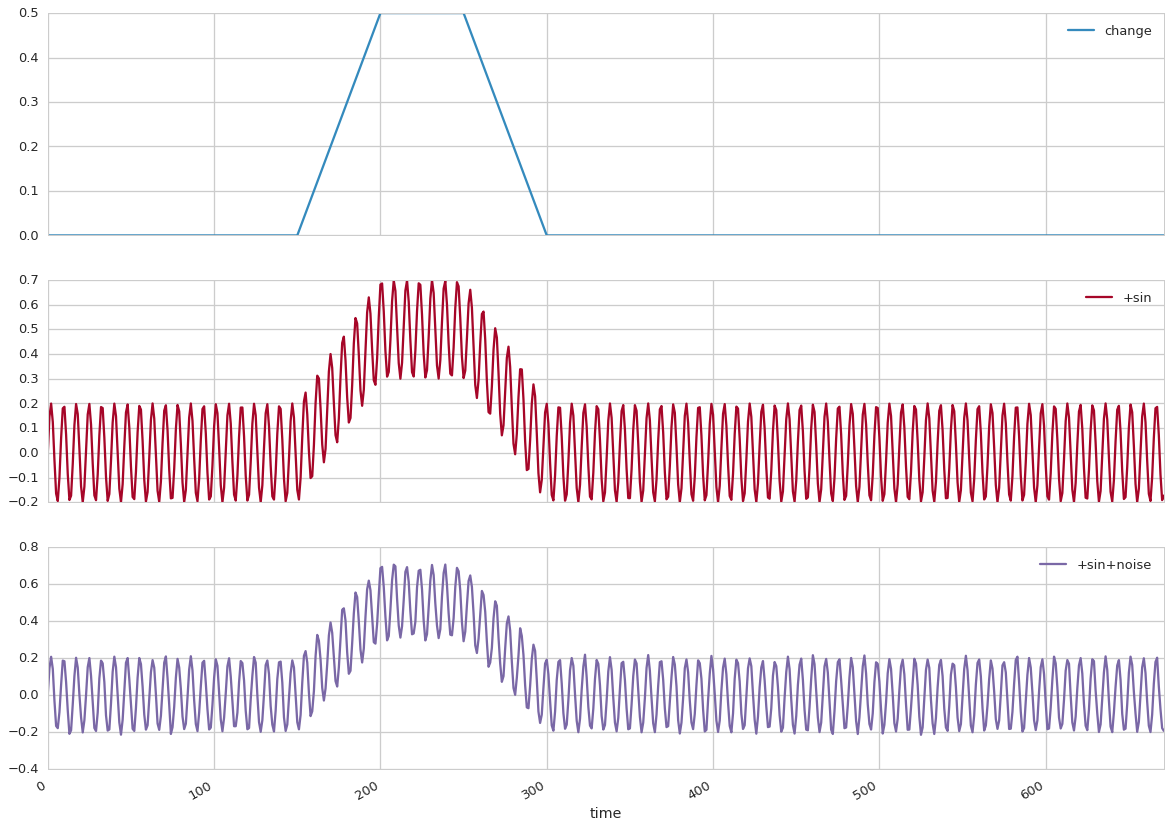
動作確認のため、わかりやすい疑似データを使います。1時間単位の時系列データを想定して、150~200期で数値が徐々に増加し、151~200期で一旦定常状態に、201~250期で再び元の水準に戻るような変化のある時系列データを作成しました。実際のデータには様々なノイズがあるので、これに24時間周期のサインカーブと、独立な乱数の成分を追加した時系列で動作確認しました。
np.random.seed(42)
T = 24 * 7 * 4
pt = (150, 200, 250)
slope = .01
test = pd.DataFrame(data={'time': range(T), # pd.date_range('2018-01-01', periods=T),
'change': [slope * (t - pt[0]) * (t in range(pt[0], pt[1]) ) +
slope * (pt[1] - pt[0]) * (t in range(pt[1], pt[2])) +
(-slope * (t - pt[2]) + slope * (pt[1] - pt[0])) * (t in range(pt[2], pt[2] + (pt[1] - pt[0]))) for t in range(T)],
}).set_index('time')
test['+sin'] = test['change'] + 0.2 * np.sin(
[2 * np.pi * t / 24.0 * np.pi for t in range(T)])
test['+sin+noise'] = test['+sin'] + np.random.normal(size=T, scale=.01)
時系列はこのようになります。ノイズを合成した、最下段の時系列データを用います。
test.plot(subplots=True, figsize=(20, test.shape[1] * 5))
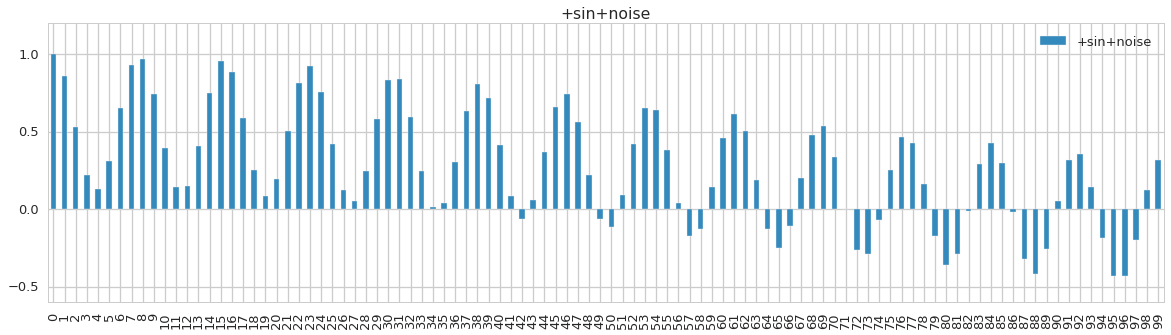
一応、系列相関をコレログラムで確認します。
test = test[['+sin+noise']]
cols = test.columns
corr = pd.DataFrame(data={x: [test[x].autocorr(l) for l in range(24*7)] for x in cols})
corr[0:100].plot(kind='bar', subplots=True, figsize=(20, 5))
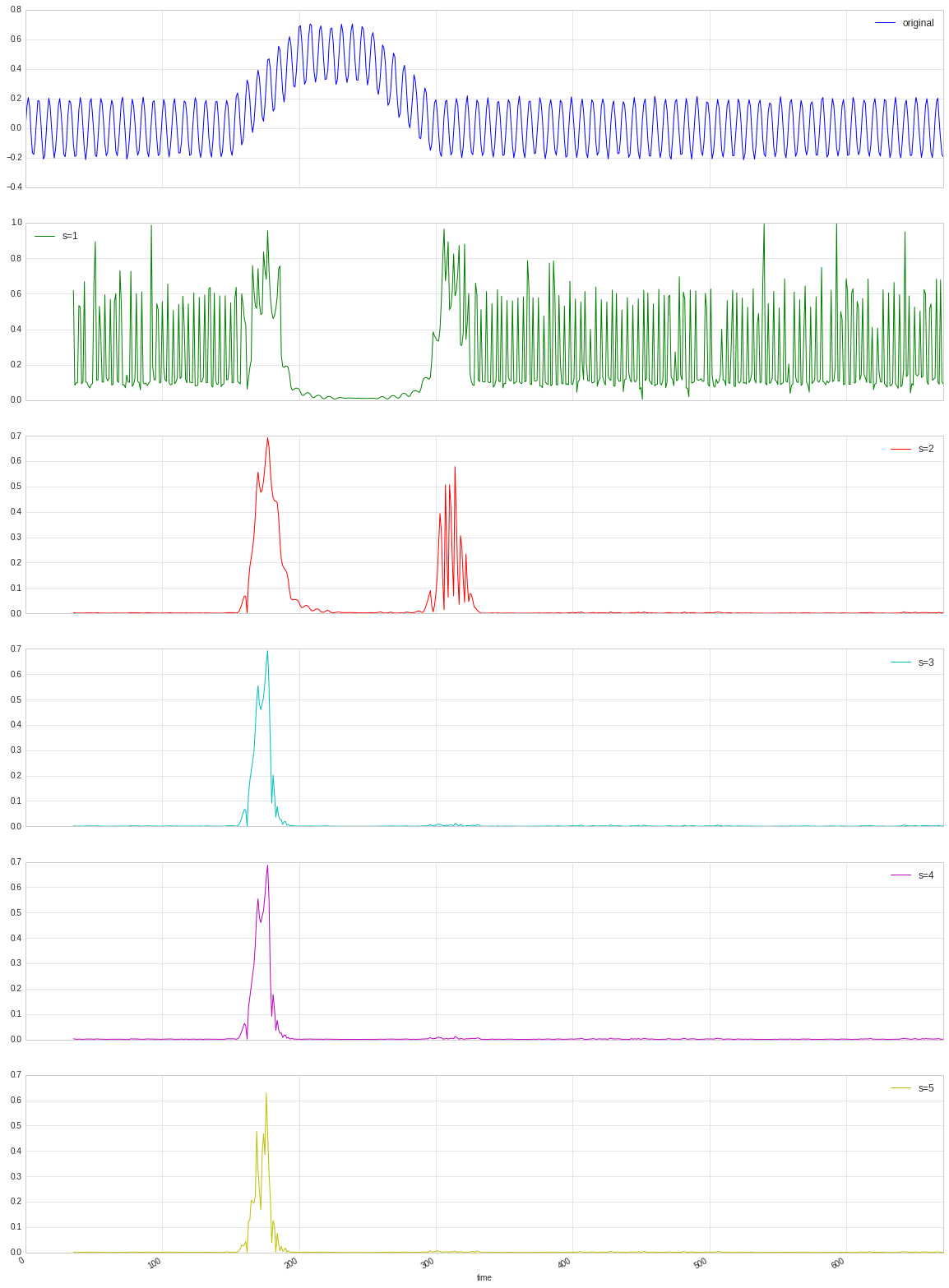
コレログラムから、24時間周期であることが確認できたので、ラグをこれに合わせて24とします。履歴行列の特異ベクトル数 s を 1~5の範囲で変えた結果をそれぞれ掲載しました。いずれの場合でも、上昇が始まる時点で異常度が高くなっていることがわかります。一方で、251期の時点から始まる変化に対して、異常度の増加が遅れてるように見えます。この期間は、比較対象である履歴行列が、すでに変化の終わった200~期中から取り出しているので、この期間の時系列が正常と認識されてしまっているからです。このような性質から、異常の定義によっては、履歴行列をとる位置を変えるのも良いかもしれません。
sst = test.copy()
sst = sst[['+sin+noise']]
sst.rename(columns={'+sin+noise': 'original'}, inplace=True)
for s in range(1, 6):
score = SSA_CD(series=sst['original'].values,
standardize=False,
w=8, lag=24, ns_h=s, ns_t=1)
sst['s={}'.format(s)] = score[0]
sst.plot(subplots=True, figsize=(20, sst.shape[1] * 5))
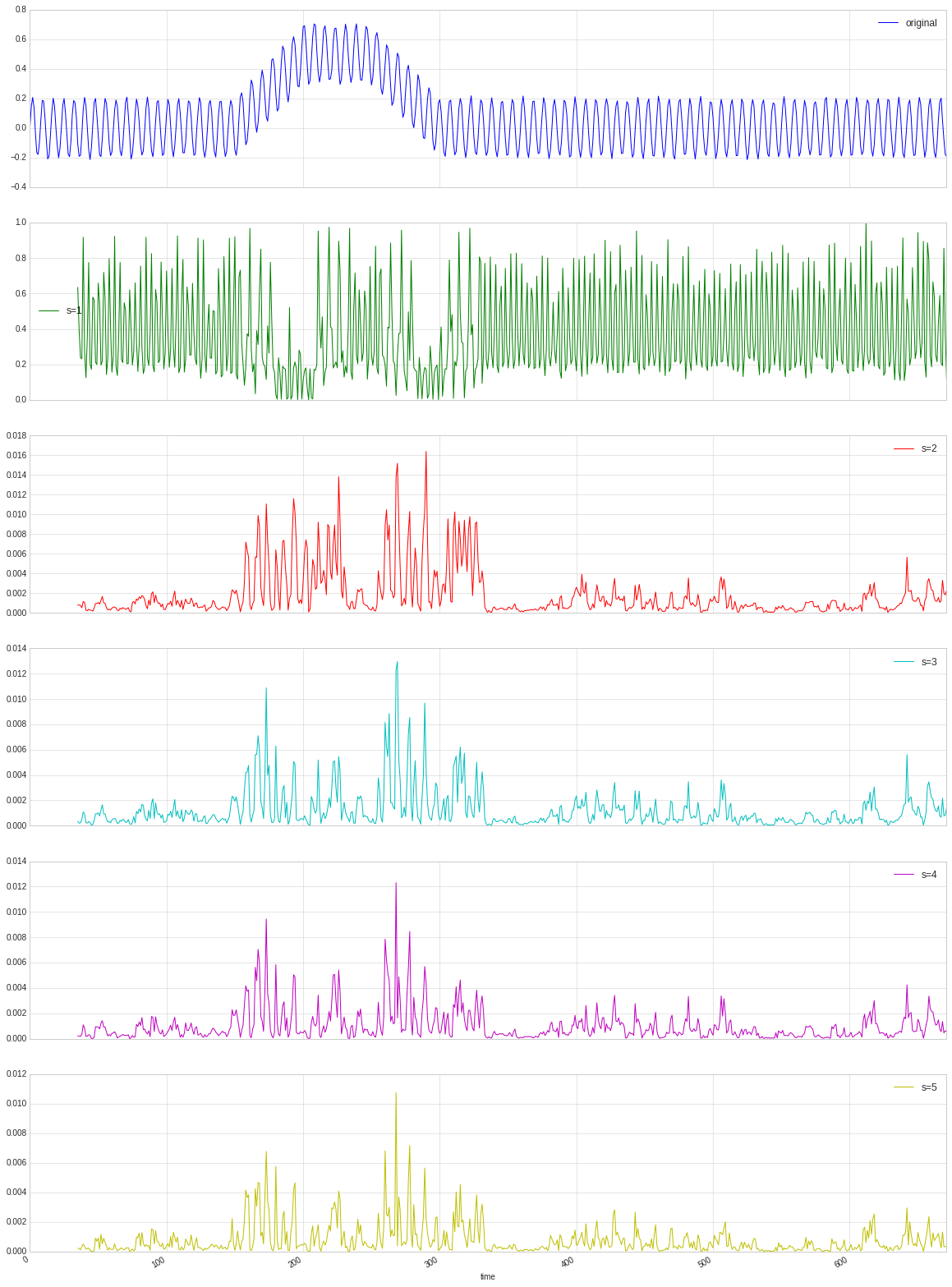
一方、標準化をすると以下のように、さらに感度が高くなるようです。また、時系列の上下シフトを除したためか、上方にシフトした201~250期中のノイズに対する感度が高くなっているのがわかります。251期からの減少ステージに対しても、すぐに反応しているのがわかります。
sst = test.copy()
sst = sst[['+sin+noise']]
sst.rename(columns={'+sin+noise': 'original'}, inplace=True)
for s in range(1, 6):
score = SSA_CD(series=sst['original'].values,
standardize=False,
w=8, lag=24, ns_h=s, ns_t=1,
normalize=True)
sst['s={}'.format(s)] = score[0]
sst.plot(subplots=True, figsize=(20, sst.shape[1] * 5))
パラメータの決め方
理論上の性質を完全に理解しているとは言いがたいですが、パラメータを調整したりした経験から、以下のような特徴がありそうです。やや雑多ですが、紹介します。
取り出す特異ベクトルの数をどうするか。
- 特異値の累積寄与率を目安に決めることにしました。
- 特異値を大きい順に $s_1, s_2, \cdots, s_n$ とすると、第i特異ベクトルの寄与率は、 $p_i = \frac{s_i}{\sum_{j=1}^n s_j}$ となり、1からi番目まで寄与率を足した
$\mathit{cp}_{i} = \sum_{j=1}^i p_j = \frac{\sum_{j=1}^i s_j}{\sum_{k=1}^n s_k}$
を累積寄与率といいます。 - これは、主成分分析でつかわれる方法です。累積寄与率はゼロから1の範囲になり、これは主成分でどれだけデータを説明できているかを意味します。小さすぎると、重要な情報を切り捨てていることになりますが、大きすぎると不要なノイズも含めてしまいます。ノイズというのは定義上、規則をもたないランダムなものなので、特異値分解した場合、特異値の小さい部分に含まれるはずです。よって、データのノイズが大きければ累積寄与率を小さく抑えたほうがいいでしょう。
- 今回の場合は、テスト行列の特異値の累積寄与率がおよそ 0.6 でした。
- テスト行列と履歴行列で、それぞれベクトルの数を変えるということもできます。この例では、テスト行列のみ第1特異ベクトルで固定しています。しかし、あまり大きな違いはないので、基本的に同じでいいと思います。
- 今回の場合は、テスト/履歴行列でそれぞれ第1、第2特異ベクトルまで使うのが適していそうです。
2つの時系列のラグ L はどうするか。
- ラグが短すぎると、時間をかけて緩やかに変化するタイプの異常を検知しづらくなりますが、一方で長すぎると発見が遅れます。
- 周期性がある場合、周期の倍数をラグにすると、周期的な変動を打ち消すことができます。例えば、今回は24時間にしました。ただし、他のパラメータ調整や前処理でも打ち消せそうです。
部分時系列の長さ w はどれくらいが良いか。
- $w$ が大きいほど、異常度グラフが滑らかになり、感度が低下します。
- 短かすぎると、周期の長い正常な変化と、異常値を区別できない可能性があります。
スライド幅 (行列 H の列数) はどれくらいが良いか
- 今回の実験では大きな違いはありませんでした。もっと複雑な波形の時系列データでは影響があるかもしれません。
課題
特異スペクトル変換は分布を仮定しないので、多様な波形の時系列データに対応できますが、一方で次のような短所があります。
- 欠損値の多い時系列データには向いていません。
- 欠損値が含まれていると特異値分解できないため
- この場合は、累積和法のように、時系列データにモデルを当てはめ残差の大きさで異常度を判定する方法が有効と思われます。
- ただし、欠損値を前後の値で補間すれば、特異スペクトル変換は可能です。
- $w, L$, 特異ベクトルの数など、データに応じて決めるべきパラメータが多いです。各パラメータの調整がどのように働くか、理論的な性質を把握できたほうが良いです。
参考文献
- Ide, Tsuyoshi and Tsuda, Koji "Change-Point Detection using Krylov Subspace Learning," 2007年
- SAM 『Fitbitから取得した心拍データで時系列の異常検知を試してみる』, 2016年
- 井出剛・杉山将 『異常検知と変化検知』, 2015年, 講談社