はじめに
傾向スコアを用いた逆確率重み付け法(以下、IPW: Inverse Probability Weighting)を用いると「なぜATEが推定できるのか」を直感的に理解できるようにイメージをまとめました。
傾向スコアを用いた因果推論の詳細については、こちらの記事にまとめておりますのでぜひご一読いただけますと幸いです。
傾向スコアとIPWの概要
以下
- X: 共変量
- T: 処置変数
- Y: アウトカム
- e(X): 傾向スコア
として、説明します。
傾向スコアとは
傾向スコアとは、属性ベクトル$X^i$から予測される処置が施される確率(すなわち、処置を受ける傾向)のことです。$$P(T_i=1|X_i) = E(T_i|X_i) = e(X_i)$$と表されます。
IPWとは
IPWとは、傾向スコアの逆数をサンプルの重みとして因果効果の推定に利用する手法です。
- 傾向スコアが大きい→サンプルの出現確率が高い
- 傾向スコアが小さい→サンプルの出現確率が低い
と考えられるため、傾向スコアの逆数をかけることで
- 出現確率の高いサンプルは、小さく重み付け
- 出現確率の低いサンプルは、大きく重み付け
することで処置群と対照群の共変量の分布を調整し、ランダム割り付けされた状態に近づけようというイメージです。
IPWを用いたATEの推定値は$$ATE = \frac{1}{N} \sum_{i=1}^N \frac{T_i}{e(X_i)}Y_i - \frac{1}{N} \sum_{i=1}^N \frac{1 - T_i}{1 - e(X_i)}Y_i \tag{1}$$あるいは$$ATE = \frac{\sum_{i=1}^N \frac{T_i}{e(X_i)}Y_i}{\sum_{i=1}^N \frac{T_i}{e(X_i)}} - \frac{\sum_{i=1}^N \frac{1 - T_i}{1 - e(X_i)}Y_i}{\sum_{i=1}^N \frac{1 - T_i}{1 - e(X_i)}} \tag{2}$$と表されます。
(1)式よりも(2)式の方が、推定量の分散が小さくなることが知られています。
Pythonによる確認
下記URLのデータをもとに「なぜIPWによってATEがうまく推定できるのか」を考えてみます。
https://zenn.dev/s1ok69oo/articles/c058108acb83e7
データの生成
上記の記事に従って、Pythonでデータを作成します。
# 必要なライブラリをインポート
import numpy as np
import pandas as pd
# シードの設定
np.random.seed(0)
# データのサイズ
size = 120
# 学習意欲を表す変数X1(交絡因子)
X1 = np.random.uniform(0, 1, size)
# 理系出身ダミーX2(交絡因子)
X2 = np.random.choice([0, 1], p=[0.5, 0.5], size=size)
# 特講受講ダミーT(処置変数)
T_noise = np.random.uniform(0, 0.5, size)
T_threshold = 0.25*X1 + 0.25*X2 + T_noise
T = np.where(T_threshold>=0.5, 1, 0)
# 試験の得点Y
Y_noise = np.random.normal(0, 10, size)
Y = np.clip(40*X1 + 20*X2 + 20*T + Y_noise, 0, 100).astype("int")
# データフレームに格納し、5つだけ出力
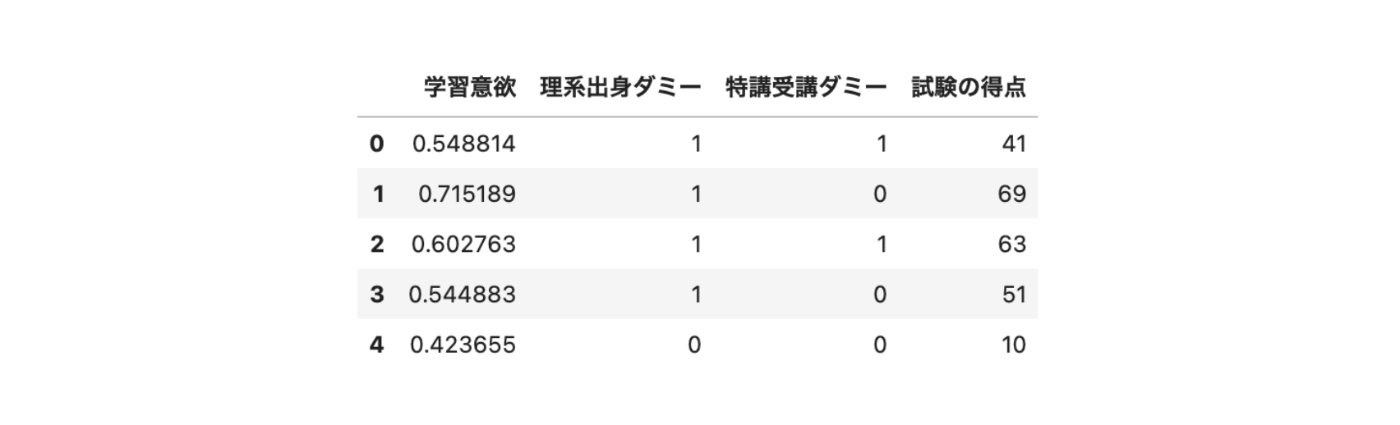
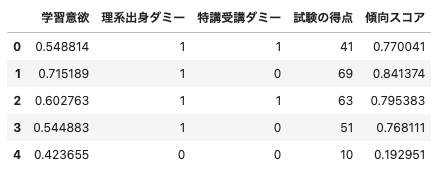
df = pd.DataFrame({"学習意欲": X1, "理系出身ダミー": X2, "特講受講ダミー": T, "試験の得点": Y})
df.head()
こちらのデータでは
- 共変量: 学習意欲、理系出身ダミー
- 処置変数: 特講受講ダミー
- アウトカム: 試験の得点
となります。
本来やりたいことは「特講を受講が、試験の得点にどれだけ効果があるかを調べたい」というものです。
しかし「特講の受講」と「試験の得点」は「学習意欲」や「理系出身か否か」によって影響を受けています。
そのため「特講の受講したグループの試験の平均得点」と「特講の受講していないグループの試験の平均得点」などを単純比較してしまうと、バイアスが生じてしまうというのが課題となっています。
データの分布の変化のイメージ
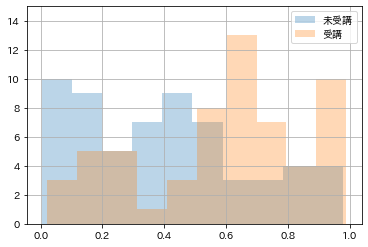
特講を受講したグループと受講していないグループの学習意欲の分布を確認します。
# ヒストグラムを描画
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib
df0 = df[df["特講受講ダミー"]==0][["学習意欲", "試験の得点"]]
df1 = df[df["特講受講ダミー"]==1][["学習意欲", "試験の得点"]]
df0["学習意欲"].hist(alpha=0.3, label="未受講")
df1["学習意欲"].hist(alpha=0.3, label="受講")
plt.legend()
plt.ylim(0, 15)
plt.show()
特講を受講したグループは学習意欲の分布が右寄り(高め)、特講を受講していないグループは学習意欲の分布が左寄り(低め)であることが分かります。
ここで、なぜ傾向スコアの逆数でサンプルに重み付けをするとバイアスのない推定量が得られる直感的な説明をさせていただきます。
たとえば、特講未受講のグループの分布を見てみます。
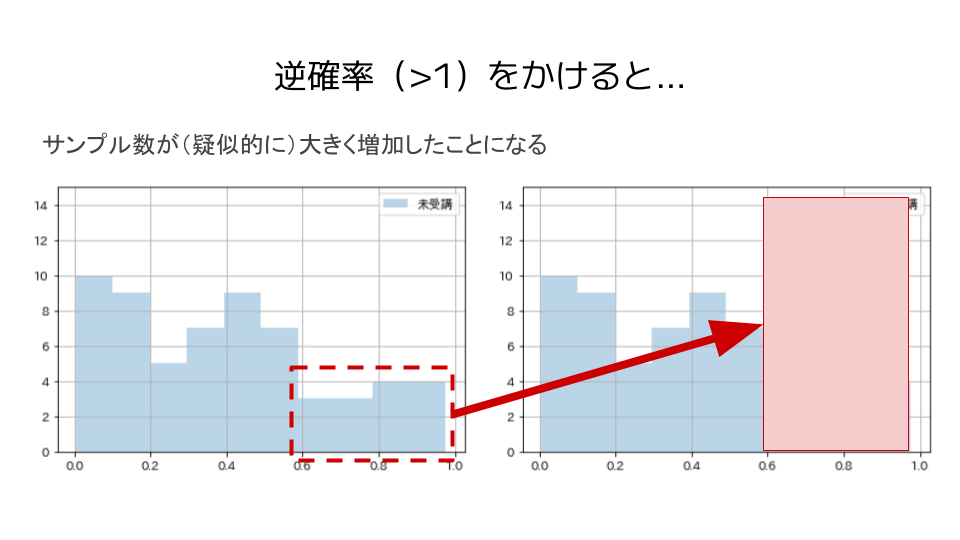
サンプルを傾向スコアの逆数(逆確率)で重み付けすると、疑似的にサンプル数は大きくなるというイメージです。
傾向スコアは0より大きく1より小さい値を取るため、逆確率は1より大きい値となります。
この際に、サンプル数が小さい部分は傾向スコアが低い(逆確率が高い)ため、逆確率をかけるとサンプル数が(疑似的に)大きく増加します。
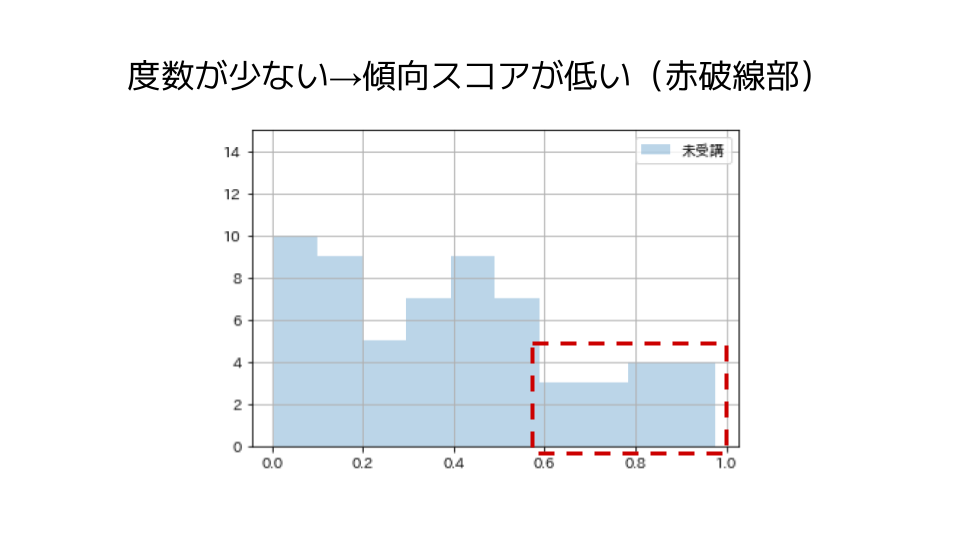
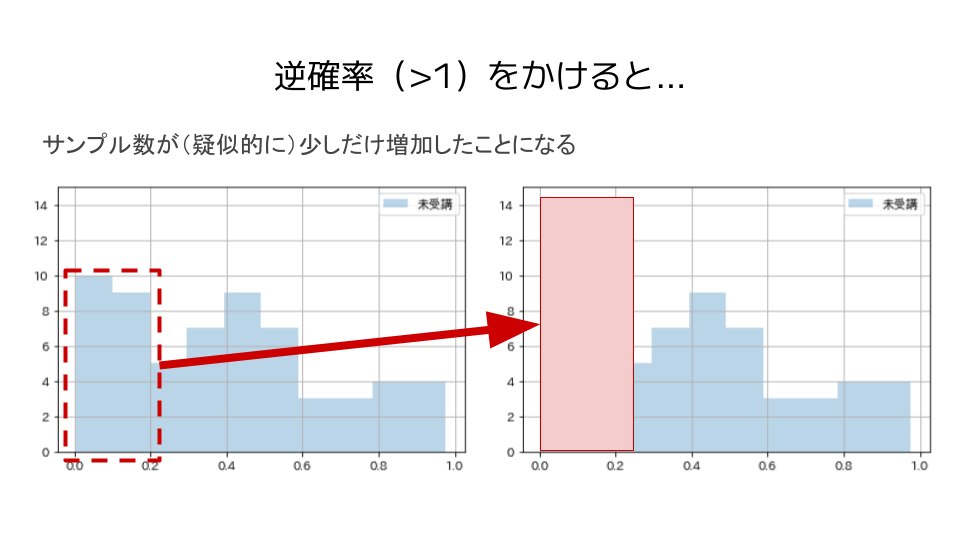
それに対し、サンプル数が大きい部分は傾向スコアが高い(逆確率が低い)ため、逆確率をかけるとサンプル数が(疑似的に)少しだけ増加します。
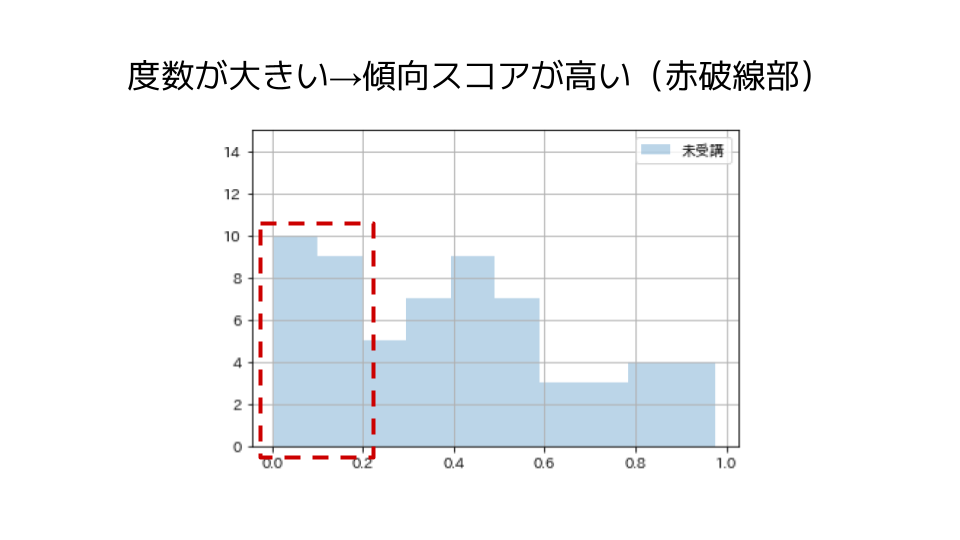
このように、サンプルを逆確率で重み付けすることで
- サンプル数が小さいところでは(疑似的に)サンプル数を大きく増加
- サンプル数が大きいところでは(疑似的に)サンプル数を少しだけ増加
させるため、全体としては共変量(今回で言えば、学習意欲)によらず(疑似的に)サンプル数が同じくらいになるというイメージです。
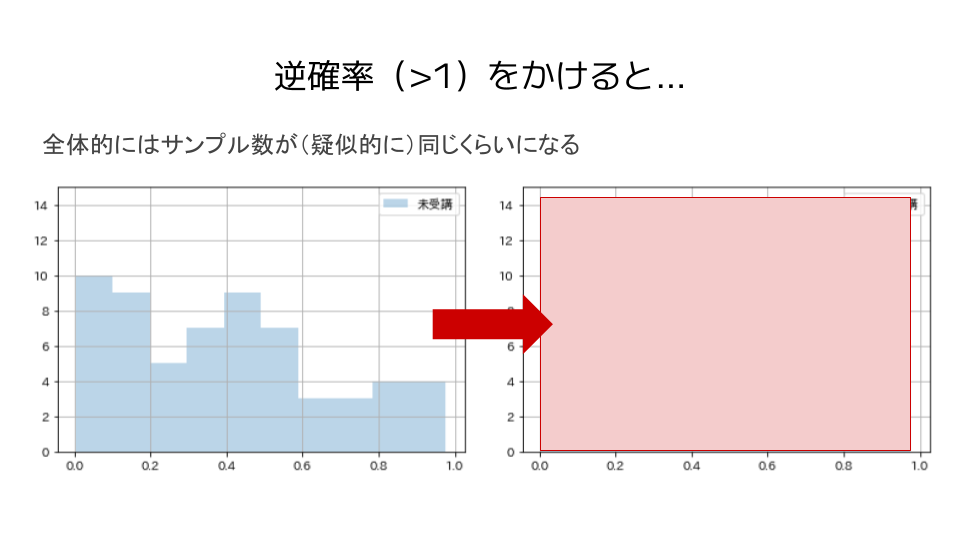
特講を受講したグループでも同様にして、結果として共変量によって偏りがあるデータから、特講を受講したグループと受講していないグループで共変量によらず処置がランダムに割り付けられたデータを疑似的に作り出すことができます。
以上が、IPWによってATEが推定できることの直感的な説明でした。
おまけ
せっかくなので、ATEの計算も行います。(ほぼ、元の記事のコピペです)
傾向スコアを計算
次に傾向スコアを計算します。
- 被説明変数: 処置変数(特講受講ダミー)
- 説明変数: 共変量(学習意欲、理系出身ダミー)
として、ロジスティック回帰を用いて処置変数が1となる確率の推定値を算出します。
# 必要なライブラリのインポート
import statsmodels.api as sm
# 傾向スコアを算出するために使用する説明変数
X = df[["学習意欲", "理系出身ダミー"]]
X = sm.add_constant(X)
# 処置変数
T = df["特講受講ダミー"]
# 傾向スコアを算出
model = sm.Logit(T, X)
result = model.fit()
result.predict(X)
df["傾向スコア"] = result.predict(X)
df.head()
ATEの算出
(1)式、(2)式の両方でATEを計算するため、どちらの式でも利用する$$\frac{T_i}{e(X_i)}Y_i, \frac{1 - T_i}{1 - e(X_i)}Y_i$$を表すカラムを作成します。
df0["IP"] = 1 / (1 - df0["傾向スコア"])
df1["IP"] = 1 / df1["傾向スコア"]
df0["IPW"] = df0["学習意欲"]*df0["IP"]
df1["IPW"] = df1["学習意欲"]*df1["IP"]
df0["IPW"].hist(alpha=0.3, label="未受講")
df1["IPW"].hist(alpha=0.3, label="受講")
(1)式、すなわち、$$ATE = \frac{1}{N} \sum_{i=1}^N \frac{T_i}{e(X_i)}Y_i - \frac{1}{N} \sum_{i=1}^N \frac{1 - T_i}{1 - e(X_i)}Y_i$$を計算すると
df1["IPW"].sum() / len(df) - df0["IPW"].sum() / len(df)
24.565426577770992
(2)式、すなわち、$$ATE = \frac{\sum_{i=1}^N \frac{T_i}{e(X_i)}Y_i}{\sum_{i=1}^N \frac{T_i}{e(X_i)}} - \frac{\sum_{i=1}^N \frac{1 - T_i}{1 - e(X_i)}Y_i}{\sum_{i=1}^N \frac{1 - T_i}{1 - e(X_i)}}$$を計算すると
df1["IPW"].sum() / df1["IP"].sum() - df0["IPW"].sum() / df0["IP"].sum()
22.526493842623854
という結果になりました。上記のデータでは特講受講による効果が20と設定されていたため、(2)式の方が良さげな推定結果になっているようです。
おわりに
最後まで読んでいただきありがとうございました。
zennにて「Python×データ分析」をメインテーマに記事を執筆しているので、ご一読いただけますと幸いです。
また、過去にLTや勉強会で発表した資料が下記リンクにてまとめてありますので、こちらもぜひご一読くださいませ。
参考文献
- 岩崎(2015)「統計的因果推論」朝倉書店
- 西山他(2019)「計量経済学」有斐閣
- 星野(2009)「調査観察データの統計科学」岩波書店