EM algorithm (Expectation–maximization algorithm)
- 😕 マークは "半信半疑", "なぜ?" と思った箇所
を意味しています.
1. KL ダイバージェンスと最尤推定の関係 (復習)
1.1. KL ダイバージェンス
- 確率変数: $x$
- 確率密度: $p(x)$
- 任意の関数: $f(x)$
- 関数の期待値
$$
\mathbb{E}_{p(x)}{[f(x)]} = \int{f(x)p(x){dx}}
$$ - KL ダイバージェンスの定義
$$
D_\text{KL}(p | q) \triangleq \int{p(x) \log{\frac{p(x)}{q(x)}} dx}
$$- $p = q$ のとき
$$
D_\text{KL}(p | p) = \int{p(x) \log{1} dx} = 0
$$ - 必ず
$$
D_\text{KL}(p | q) \geq 0
$$
- $p = q$ のとき
1.2. 最尤推定 (対数尤度の最大化)
- 真の確率分布 $p_*(x)$
- 真の確率分布から生成されたサンプルデータ ${x^{(1)}, \dots, x^{(N)}}$
- モデル化 $p_\theta (x)$
- パラメータ $\theta$
- 尤度関数
$$
\prod_{n}{p_\theta(x^{(n)})}
$$ - 対数尤度関数
$$
\log{\prod_{n}{p_\theta(x^{(n)})}} = \sum_{n}{\log{p_\theta(x^{(n)})}}
$$
\hat\theta = \color{#d62728}{\arg \max_\theta{\sum_{n}{\Big[{\log{p_\theta(x^{(n)})}}\Big]}}}
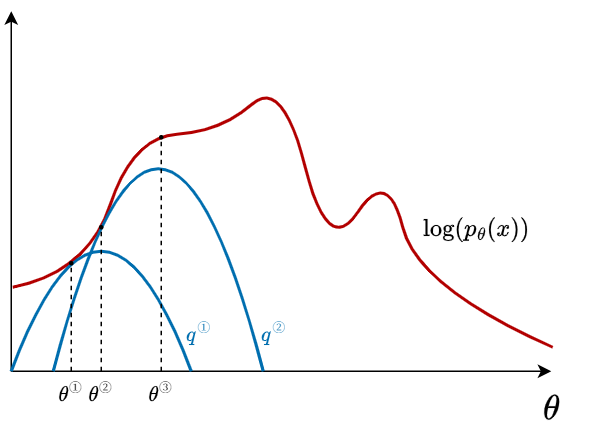
1.3. KL 距離の最小化
\begin{align*}
\hat\theta &= \arg\min_\theta{D_\text{KL}(p_* \| p_\theta)} \\
&\approx \arg\min_\theta {\cancel{\frac{1}{N}}{\sum_n{\Big[ \log{\frac{p_*(x^{(n)})}{p_\theta(x^{(n)})}} \Big]}}} \\
&= \arg\min_\theta {{\sum_n{\Big[ \cancel{\boxed{\log{p_*(x^{(n)})}}} - {\log{p_\theta(x^{(n)})}} \Big]}}} &(\text{定数項を除去}) \\
&= \color{#d62728}{\arg\max_\theta {{\sum_n{\Big[ {\log{p_\theta(x^{(n)})}} \Big]}}}} \\
\end{align*}
1.4. 結論
(1) 式と (2) 式は同じ式のため, KL 距離を最小化する $\theta$ と対数尤度を最大化する $\theta$ は等しいことが示された.
2. EM アルゴリズムの導出
- 潜在変数: $z$
- 確率変数: $x$ (観測可能)
- モデルのパラメータ: $\theta$
- データセット: $\mathcal{D} = {x^{(1)}, \dots, x^{(N)}}$
2.0. おさらい: 周辺化とは
$$
\boxed{\log{p_\theta(x)}} = \log{\Big[ \sum_z{p_\theta(x, z)} \Big]}
$$
2.1. 潜在変数つきのモデルの対数尤度関数
$$
\begin{align*}
\log{p_\theta(\mathcal{D})} &= \log{\Big[{\prod_n{p_\theta(x^{(n)})}}\Big]} \
&= \sum_n{\Big[\boxed{\log{p_\theta(x^{(n)})}}\Big]} \
&= \sum_n{\Big[{\log{\Big( \sum_{z^{(n)}}{p_\theta(x^{(n)}, z^{(n)})} \Big)}}\Big]}
\end{align*}
$$
log-sum の形なので, 解析的に解けない.
→ EM アルゴリズムを利用して, sum-log にする.
2.2. データ数が 1 つの場合
\begin{align*}
&\log{p_\theta(x)} &\downarrow \text{ベイズの定理より} \\
&= \log{\frac{p_\theta(x,z)}{p_\theta(z|x)}} &\downarrow \frac{q(z)}{q(z)} = 1 \text{を乗算する} \\
&= \log{\frac{p_\theta(x,z)}{p_\theta(z|x)}\frac{q(z)}{q(z)}} \\
&= \color{#d62728}{\boxed{\log{\frac{p_\theta(x,z)}{q(z)}} + \log{\frac{q(z)}{p_\theta(z|x)}}}}
\end{align*}
\begin{align*}
\log{p_\theta(x)} &\downarrow \sum_z{q(z) = 1} \text{を掛ける} \\
&= \log{p_\theta(x)} \sum_z{q(z)} \\
&= \sum_z{\Big[{q(z)\log{p_\theta(x)}}\Big]} \\
&= \sum_z{q(z)\Big[ \color{#d62728}{\boxed{\log{\frac{p_\theta(x,z)}{q(z)}} + \log{\frac{q(z)}{p_\theta(z|x)}}}} \Big]} \\
&= \sum_z{\Big[q(z)\log{\frac{p_\theta(x,z)}{q(z)}}\Big]} + \color{#1f77b4}{\boxed{\sum_z{\Big[q(z)\log{\frac{q(z)}{p_\theta(z|x)}}\Big]}}} \\
&= \color{#2ca02c}{\boxed{\sum_z{\Big[q(z)\log{\frac{p_\theta(x,z)}{q(z)}}\Big]}}} + \color{#1f77b4}{\boxed{D_\text{KL}\big[q(z) \| p_\theta(z|x)\big]}} \\
&\downarrow \text{KL 距離は 0 以上のため} \\
&\geq \color{#2ca02c}{\boxed{\sum_z{\Big[q(z)\log{\frac{p_\theta(x,z)}{q(z)}}\Big]}} \triangleq \text{ELBO}(x;q,\theta)} \tag{1}
\end{align*}
つまり, $\text{対数尤度} = \color{#2ca02c}{\text{ELBO項}} + \color{#1f77b4}{\text{KL項}}$ と表せる.
重要な点は, 対数尤度 $\log{p_\theta(x)}$ 自体には, $q(z)$ は含まれていないため, $q(z)$ によらず ELBO 項と KL 項の和は一定であるということ.
$q(z)$ と $p_\theta(z|x)$ が完全に一致するとき, KL 項が 0 となり, $\log{p_\theta(x)} = \text{ELBO}(x;q,\theta)$ となる.
2.3. EM アルゴリズム
E ステップ
$q(z)$ を更新して ELBO を $\log{p(x;\theta)}$ に近づける.
\begin{align*}
\text{ELBO}(x;q=p_{\theta_{old}}(z|x),\theta)
&= \sum_z{\Big[q(z)\log{\frac{p_\theta(x,z)}{p_{\theta_{old}}(z|x)}}\Big]} \\
&= \mathbb{E}_{p_{\theta_{old}}(z|x)}{\Big[ \log{\frac{p_\theta(x,z)}{p_{\theta_{old}}(z|x)}} \Big]} \tag{2}
\end{align*}
M ステップ
(2) 式を $\theta$ で微分して勾配法で $\theta$ を更新する.
ELBO の値を上げることで, "間接的に" $\log{p(x;\theta)}$ の値を押し上げる.
図解
EM アルゴリズムにおける対数尤度の単調増加性
$\log[p(x;\theta_\text{new})] \geq \log[p(x;\theta_\text{old})]$ が常に成り立つ. (証明は省略)
2.4. 複数データへの拡張
- 違いは, $\sum_n$ がつくだけ.
- $x \rightarrow { x^{(1)}, \dots, x^{(N)} }$
- $q \rightarrow { q^{(1)}, \dots, q^{(N)} }$
$$
\sum_n{\Big[{\log{\Big( \sum_{z^{(n)}}{p_\theta(x^{(n)}, z^{(n)})} \Big)}}\Big]} \geq \sum_n{\text{ELBO}(x^{(n)};q^{(n)},\theta)}
$$
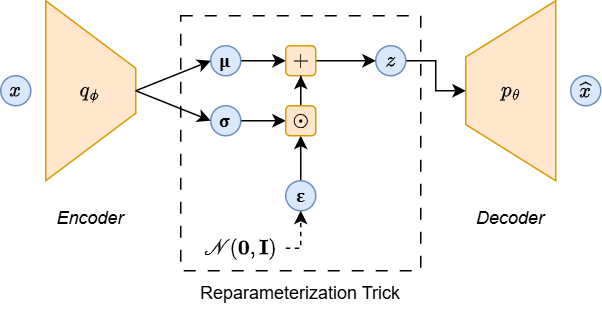
3. VAE (Variational Autoencoder: 変分オートエンコーダ)
Reparameterization Trick により, Encoder → Decoder 間が決定的な演算でつながり, Decoder → Encoder へと逆伝播が可能になる.
3.1. ELBO の導出
(1) 式より
$$
\text{ELBO}(x;q,\theta)
\triangleq
\sum_z{\Big[q(z)\log{\frac{p_\theta(x,z)}{q(z)}}\Big]}
$$
任意の $q(z)$ だと扱いが難しいため, $q(z)$ を正規分布に限定する.
パラメータを $\mathbf{\psi}$ として,
- $q_\psi(\mathbf{z}) = \mathcal{N}(\mathbf{z}; \mathbf{\mu}, \mathbf{\Sigma})$
- $\mathbf{\psi} = \big\lbrace {\mathbf{\mu}, \mathbf{\Sigma}} \big\rbrace$
とする.
つまり,
$$
{\text{ELBO}(x;q,\theta)}
\rightarrow
{\text{ELBO}(x;\theta,\psi)}
$$
と変形された.
データ数が $N$ 個の場合, $\psi$ も ${\psi^{(1)}, \dots, \psi^{(N)}}$ の $N$ 個用意する必要がある. (計算量がデータ数に応じて増える)
そこで, 単一のパラメータ $\phi$ (ベクトル) を持つ関数を用意し, 式を置き換える. (償却推論 (Amortized Inference))
$$
\begin{align*}
\text{ELBO}(x;\theta,\psi) &= \int{q_\psi(z) \log{\frac{p_\theta(x,z)}{q_\psi(z)}}}dz \
& \downarrow \
\text{ELBO}(x;\theta,\phi) &= \int{q_\phi(z|x) \log{\frac{p_\theta(x,z)}{q_\phi(z|x)}}}dz
\end{align*}
$$
3.2. ELBO の式変形
\begin{align*}
&\text{ELBO}(x;\theta,\phi) \\
&= {\int{q_\phi(z|x)\log{\frac{\boxed{p_\theta(x,z)}}{q_\phi(z|x)}}}dz} &\downarrow {p_\theta(x,z) = p_\theta(x|z)p(z)} \\
&= {\int{q_\phi(z|x)\log{\frac{p_\theta(x|z)p(z)}{q_\phi(z|x)}}}dz} &\downarrow {\text{項を分割する}} \\
&= {\int{q_\phi(z|x)\log{p_\theta(x|z)}}dz} + {\int{q_\phi(z|x)\log{\frac{p(z)}{q_\phi(z|x)}}}dz} &\downarrow {\log{\frac{A}{B}} = -\log{\frac{B}{A}}} より \\
&= \color{#d62728}{\boxed{\int{q_\phi(z|x)\log{p_\theta(x|z)}}dz}} - \color{#1f77b4}{\boxed{\int{q_\phi(z|x)\log{\frac{q_\phi(z|x)}{p(z)}}}dz}} \\
&= \color{#d62728}{\boxed{\mathbb{E}_{q_\phi(z|x)}{\Big[\log{p_\theta(x|z)}\Big]}}} - \color{#1f77b4}{\boxed{D_\text{KL}{\big[q_\phi(z|x) \| p(z)\big]}}} \\
&= \color{#d62728}{J_1} + \color{#1f77b4}{J_2}
\end{align*}
$\color{J_1}$ の計算
$$
\begin{align*}
\mathbf{\mu}, \mathbf{\Sigma} &= \text{Decoder}(\mathbf{x};\mathbf{\phi}) \
\mathbf{z} &\sim \mathcal{N}{(\mathbf{z}; \mathbf{\mu}, \mathbf{\sigma}^2 \mathbf{I})} \
\mathbf{\hat{x}} &= \text{Encoder}(\mathbf{z};\mathbf{\theta})
\end{align*}
$$
なので, $J_1$ は以下のように近似できる. (😕)
$$
\begin{align*}
J_1 &\approx \log{\mathcal{N}(\mathbf{x}; \mathbf{\hat{x}}, \mathbf{I})} \
&= \log{\Big[\frac{1}{\sqrt{(2\pi)^D} \cancel{|\mathbf{I}|}} - \exp{\big[ \frac{1}{2}(\mathbf{x}-\mathbf{\hat{x}})^{T}{\cancel{\mathbf{I}^{-1}}}(\mathbf{x}-\mathbf{\hat{x}}) \big]}\Big]} \
&= \log{\frac{1}{\sqrt{(2\pi)^D}}} - \frac{1}{2}(\mathbf{x}-\mathbf{\hat{x}})^{T}(\mathbf{x}-\mathbf{\hat{x}})
\end{align*}
$$
!!!
多変量正規分布 (ベクトルの正規分布) の確率密度関数
$$
\begin{align*}
\mathbf{x} &\sim \mathcal{N}(\mathbf{\mu}, \mathbf{\Sigma}) \
p(\mathbf{x}) &= \frac{1}{\sqrt{(2\pi)^D |\mathbf{\Sigma}|}} \exp{\Big[-\frac{1}{2}(\mathbf{x}-\mathbf{\mu})^T \mathbf{\Sigma}^{-1} (\mathbf{x}-\mathbf{\mu})\Big]}
\end{align*}
$$
$\color{#1f77b4}{J_2}$ の計算
\begin{align*}
J_2 &= D_{\text{KL}}(q_\phi(\mathbf{z}|\mathbf{x}) \| p(\mathbf{z})) \\
&= D_{\text{KL}}(q_\phi(\mathbf{z}|\mathbf{x}) \| \mathcal{N}(\mathbf{0}, \mathbf{I})) &\downarrow (\text{解析的に求まる}) \\
&= \frac{1}{2}{\sum_h{\Big[1 + \log{\sigma_h^2 - \mu_h^2 - \sigma_h^2} \Big]}} &(h\text{は}\mathbf{z}\text{の次元数})
\end{align*}
3.3. VAE の目的関数まとめ
\begin{align*}
\text{ELBO}(x;\theta,\phi)
&= \color{#d62728}{J_1} + \color{#1f77b4}{J_2} \\
&\approx \color{#d62728}{-\frac{1}{2}(\mathbf{x}-\mathbf{\hat{x}})^{T}(\mathbf{x}-\mathbf{\hat{x}})} + \color{#1f77b4}{\frac{1}{2}{\sum_h{\Big[1 + \log{\sigma_h^2 - \mu_h^2 - \sigma_h^2}\Big]}}} + \textrm{C} \\
&= \color{#d62728}{再構成誤差項} + \color{#1f77b4}{正則化項} + \textrm{C}
\end{align*}
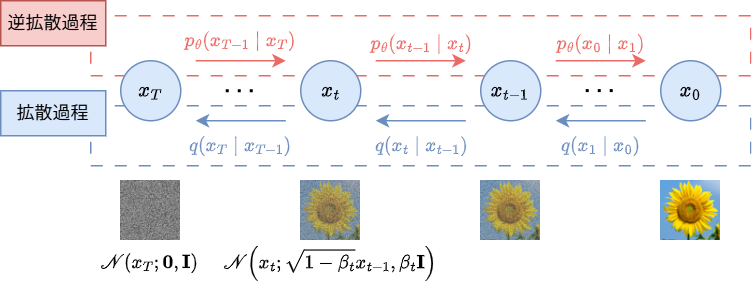
4. DDPM (Denoising Diffusion Probabilistic Model: 拡散モデル)
4.1. 階層型 VAE (Ladder Variational Autoencoder)
4.2. 階層型 VAE → 拡散モデル
- 観測変数はと潜在変数の次元数を同じにする.
- エンコーダは, パラメータを持たない正規分布によるノイズを付加する.
- 拡散過程のパラメータはなし (固定正規分布)
- ${\beta_{1}, \dots, \beta_{T}}$ は固定値だが, 決め方にいくつか手法がある.
4.3. 拡散モデル
4.3.1. 尤度関数の導出
VAE の ELBO より
\text{ELBO}(x; \theta, \phi) = \int{q_\phi(z|x) \log{{\frac{p_\theta(x, z)}{q_\phi(z|x)}}}}dz
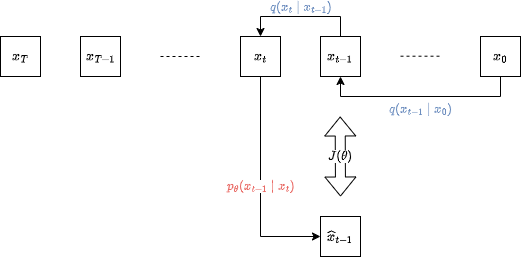
$x \rightarrow x_0$, $z \rightarrow x_1, \dots, x_T$ に置き換えて
\begin{align*}
\text{ELBO}(x_0; \theta)
&= \mathbb{E}_{q(x_1,\dots,x_T|x_0)}{\Big[{\log{\frac{p_\theta(x_0, \dots, x_T)}{q(x_1, \dots, x_T|x_0)}}}\Big]} \\
&= \mathbb{E}_{q(x_{1:T}|x_0)}{\Big[{\log{\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}}}\Big]}
\end{align*}
ここで,
\begin{cases}
q(x_t|x_{t-1}) = \mathcal{N}(x_t;\sqrt{1-\beta_t}x_{t-1}, \beta_t \mathbf{I})\\
x_t = \sqrt{1-\beta_t}{x_{t-1}} + \sqrt{\beta_t}{\epsilon} \\
\epsilon \sim \mathcal{N}(x_{t-1}; \hat{x}_{t-1}, I) \\
T \rightarrow \infty
\end{cases}
とすると
p(x_T) \approx \mathcal{N}(x_T; \mathbf{0}, \mathbf{I})
となる.
またニューラルネットワークによる逆拡散過程は
p_\theta(x_{t-1}|x_t) = \mathcal{N}(x_{t-1}; \hat{x}_{t-1}, \mathbf{I})
となる.
(つづき)
\begin{align*}
\text{ELBO}(x_0; \theta)
&= \mathbb{E}_{q(x_{1:T}|x_0)}{\Big[{\log{\frac{p_\theta(x_{0:T})}{q(x_{1:T}|x_0)}}}\Big]} \\
&= \mathbb{E}_{q(x_{1:T}|x_0)}{\Big[{\log{\frac{\cancel{p(x_T)} \prod p_\theta(x_{t-1}|x_t)}{\cancel{\prod{q(x_t|x_{t-1})}}}}}\Big]} & (\theta に関係ない項を除去) \\
J(\theta) &= \mathbb{E}_{q(x_{1:T}|x_0)}{\Big[{\log{\prod p_\theta(x_{t-1}|x_t)}}\Big]} \\
\end{align*}
\begin{align*}
J(\theta)
&= \mathbb{E}_{q(x_{1:T}|x_0)}{\Big[{\sum_t{\log p_\theta(x_{t-1}|x_t)}}\Big]} \\
&= \sum_t{\mathbb{E}_{q(\color{red}{\boxed{x_{1:T}}}|x_0)}\Big[{\log p_\theta(x_{t-1}|x_t)}\Big]} & (\downarrow \text{期待値の中身に関係ない確率分布の確率変数は消去できる}) \\
&= \sum_t{\mathbb{E}_{q(\color{red}{\boxed{x_{t-1}, x_t}}|x_0)}\Big[{\log p_\theta(x_{t-1}|x_t)}\Big]} \\
&= T \mathbb{E}_{u(t)}\Big[{\mathbb{E}_{q(x_{t-1}, x_t|x_0)}\big[{\log p_\theta(x_{t-1}|x_t)}\big]}\Big]
\end{align*}
\begin{cases}
t \sim U\{1,T\} \\
x_{t-1} \sim q(x_{t-1}|x_0) \\
x_t \sim q(x_t|x_{t-1})
\end{cases}
としてサンプリングし (サンプルサイズは 1) モンテカルロ法による近似により,
J(\theta) \approx T \log{p_\theta(x_{t-1}|x_t)}
ここで
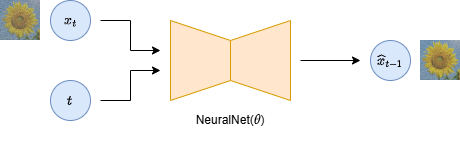
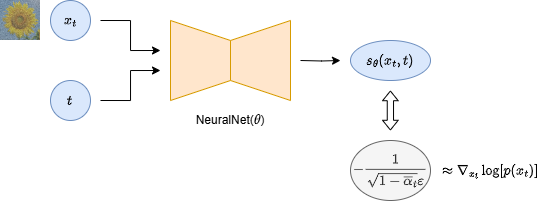
\begin{align*}
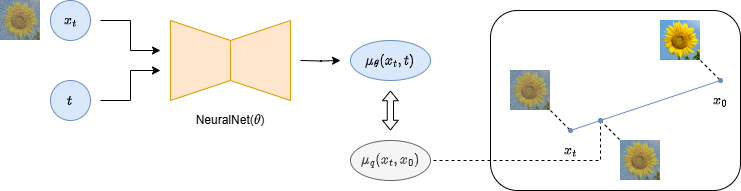
\hat{x}_{t-1} &= \text{NeuralNet}(x_t, t; \theta) \\
p_\theta(x_{t-1}|x_t) &= \mathcal{N}{(x_{t-1}; \hat{x}_{t-1}, \mathbf{I})}
\end{align*}
となるため,
$$
J(\theta) \approx -\frac{T}{2}{{|{x_{t-1} - \hat{x}_{t-1}}|}^2}
$$
と近似できる.
サンプリングの流れを図示すると
ちなみに, $q(x_t|x_0)$ は解析的に以下のように解析的に計算できる (証明は省略).
q(x_t|x_0) = \mathcal{N}(x_t;\sqrt{\bar{\alpha}_t}x_0, (1-\bar{\alpha}_t) \mathbf{I})
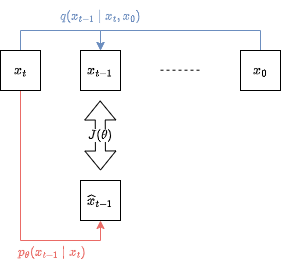
4.3.2. 改良 (計算量の削減)
\begin{align*}
J(\theta)
&= \sum_t{\Big[{\mathbb{E}_{q(x_{t-1}, x_t|x_0)}{\big[{\log{p_\theta(x_{t-1}|x_t)}}\big]}}\Big]} \\
&= T \mathbb{E}_{u(t)}{\big[{J_0(\theta)}\big]} \\
J_1(\theta)
&= J_0(\theta) - \boxed{\mathbb{E}_{q(x_{t-1}, x_t|x_0)}{\big[{\log{q(x_{t-1}, x_t|x_0)}}\big]}} & (\theta に関係ない項を追加しても, \theta^* は変わらない) \\
&= \int\int{\color{red}{\boxed{q(x_{t-1}, x_t|x_0)}}\log{\frac{p_\theta(x_{t-1}|x_t)}{q(x_{t-1}, x_t|x_0)}}}{d{x_{t-1}}}{d{x_{t}}} \\
&= \int\int{\color{red}{\boxed{q(x_t|x_0) q(x_{t-1}|x_t,x_0)}}\log{\frac{\color{blue}{\boxed{p_\theta(x_{t-1}|x_t)}}}{\color{green}{\boxed{q(x_{t-1}, x_t|x_0)}}}}}{d{x_{t-1}}}{d{x_{t}}} \\
&= -\int\int{q(x_t|x_0) q(x_{t-1}|x_t,x_0)\log{\frac{\color{green}{\boxed{q(x_{t-1}, x_t|x_0)}}}{\color{blue}{\boxed{p_\theta(x_{t-1}|x_t)}}}}}{d{x_{t-1}}}{d{x_{t}}} \\
&= -\int{q(x_t|x_0)\color{red}{\boxed{\int{q(x_{t-1}|x_t,x_0)\log{\frac{q(x_{t-1}, x_t|x_0)}{p_\theta(x_{t-1}|x_t)}}}d_{x_{t-1}}}}}d{x_t} \\
&= -\int{q(x_t|x_0)\color{red}{\boxed{D_\text{KL}(q(x_{t-1}|x_t,x_0) \| p_\theta(x_{t-1}|x_t))}}}d{x_t} \\
&= -\mathbb{E}_{q(x_t|x_0)}\Big[{D_\text{KL}\big(q(x_{t-1}|x_t,x_0) \| p_\theta(x_{t-1}|x_t)\big)}\Big]
\end{align*}
$D_\text{KL}\big(q(x_{t-1}|x_t,x_0) | p_\theta(x_{t-1}|x_t)\big)$ について,
$$
\begin{cases}
q(x_{t-1}|x_t,x_0) &= \mathcal{N}(\mathbf{x_{t-1}}; \mathbf{\mu_q(x_t, x_0)}, {\sigma_q}^2(t) \mathbf{I}) \
p_\theta(x_{t-1}|x_t) &= \mathcal{N}(\mathbf{x_{t-1}}; {\mu_\theta(\mathbf{x_t}, t), \sigma_q^2(t)}\mathbf{I})
\end{cases}
$$
のため,
$$
\begin{align*}
D_\text{KL}\big[q(x_{t-1}|x_t,x_0) | p_\theta(x_{t-1}|x_t)\big]
&= \frac{1}{2 \sigma_q^2(t)}{|{\mu_\theta(\mathbf{x_t}, t)} - \mathbf{\mu_q(x_t, x_0)}|}^2
\end{align*}
$$
ただし,
\begin{align*}
{\alpha}_{t} &= 1 - {\beta}_{t} \\
{\bar{\alpha}}_{t} &= {\alpha}_{t} {\alpha}_{t-1} \dots {\alpha}_{1} = \prod_{i=1}^{t}{\alpha_i} \\
\mu_q(x_t, x_0) &= \frac{{\sqrt{{\alpha}_{t}} (1-\bar{\alpha}_{t-1}) x_t} + {\sqrt{{\bar{\alpha}}_{t-1}} (1-\alpha_{t}) x_0}}{1 - \bar{\alpha}_{t}} \\
\sigma_q^2(t) &= \frac{(1 - \alpha_t)(1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t}
\end{align*}
$\mu_\theta(\mathbf{x_t}, t)$ は, ニューラルネットワークの出力.
まとめると, $J(\theta)$ は
\begin{align*}
J(\theta)
&= -{T} \mathbb{E}_{u(t)} \Bigg[ \mathbb{E}_{q(x_t|x_0)}{\Big[ \frac{1}{{2} \sigma_q^2(t)}{\|{\mu_\theta(\mathbf{x_t}, t)} - \mathbf{\mu_q(x_t, x_0)}\|}^2 \Big]} \Bigg]
\end{align*}
損失関数は, 定数項を消去 + 符号反転して
\begin{align*}
L(\theta)
&= \cancel{-}\cancel{T} \mathbb{E}_{u(t)} \Bigg[ \mathbb{E}_{q(x_t|x_0)}{\Big[ \frac{1}{\cancel{2} \sigma_q^2(t)}{\|{\mu_\theta(\mathbf{x_t}, t)} - \mathbf{\mu_q(x_t, x_0)}\|}^2 \Big]} \Bigg] \\
&= \mathbb{E}_{u(t)} \Bigg[ \mathbb{E}_{q(x_t|x_0)}{\Big[ \frac{1}{\sigma_q^2(t)}{\|{\mu_\theta(\mathbf{x_t}, t)} - \mathbf{\mu_q(x_t, x_0)}\|}^2 \Big]} \Bigg]
\end{align*}
最終的に, サンプルサイズを 1 としたモンテカルロ法により, 以下の様に近似できる.
\begin{align*}
t &\sim U\{1, T\} \\
x_t &\sim q(x_t|x_0) \\
L(\theta) &\approx \frac{1}{\sigma_q^2(t)}{\|{\mu_\theta(\mathbf{x_t}, t)} - \mathbf{\mu_q(x_t, x_0)}\|}^2
\end{align*}
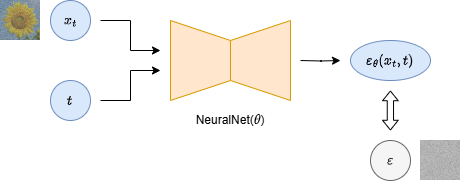
4.3.3. モデル設計
モデル設計はいろいろ考えられる.
実験した結果, ノイズを予測する設計 (③ のもの) が最も精度が高かった, とのこと.
① 前時刻のノイズ画像を予測するモデル
② 元画像を予測するモデル
③ 付加されたノイズを予測するモデル
4.3.4. データ生成プロセス
"③ 付加されたノイズを予測するモデル" での生成プロセス
- $\mathbf{x_T} \sim \mathcal{N}(\mathbf{0}, \mathbf{I})$ より, $x_T$ を決定
- 繰り返し ($t=[T, \dots, 1]$)
- $\epsilon$ 決定
\begin{cases} \epsilon \sim \mathcal{N}(\mathbf{0}, \mathbf{I}) & (t > 1) \\ \epsilon \leftarrow \mathbf{0} \end{cases} - $\sigma_q(t)$ の計算
\sigma_q(t) = \sqrt{\frac{(1-{\alpha}_t)(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}} - $\mathbf{x_{t}}$ から $\mathbf{x_{t-1}}$ の生成
\mathbf{x_{t-1}} = \frac{1}{\sqrt{\alpha}_{t}}{\Big({\mathbf{x_t} - \frac{1-{\alpha}_{t}}{\sqrt{1-\bar{\alpha}_{t}}} \mathbf{\epsilon_\theta}(\mathbf{x_t}, t)}\Big)} + \sigma_q(t) \epsilon
- $\epsilon$ 決定
5. Positional Encoding
時刻 $t$ をニューラルネットワークに入力するときの工夫.
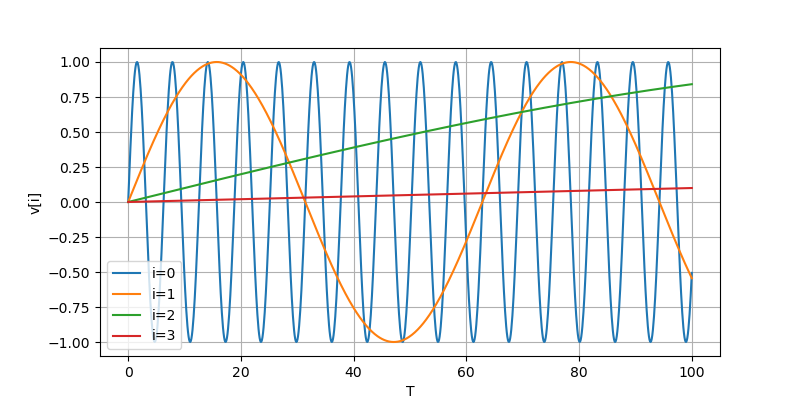
5.1. 正弦波位置エンコーディング
- 整数 $t$ を ベクトル $\mathbf{v}$ へ変換することを考える.
- ベクトル $\mathbf{v}$ の要素数 (次元数) は $D$.
グラフに視覚化すると, 以下のようになる.
$$
\mathbf{v}_i =
\begin{cases}
\sin{\big(\frac{t}{10000^{\frac{i}{D}}}\big)} & (i \text{が偶数のとき}) \
\cos{\big(\frac{t}{10000^{\frac{i}{D}}}\big)} & (i \text{が奇数のとき})
\end{cases}
$$
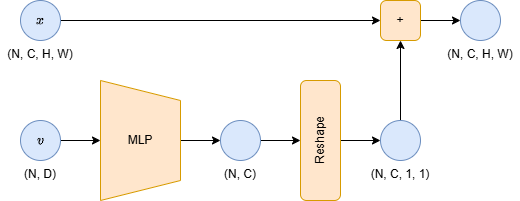
5.2. 実際にプログラムに組み込むとき
- U-Net の各 ConvBlock へ MLP を通して $(N, D)$ → $(N, C)$ へ非線形変換する.
- $(N, C)$ を $(N, C, 1, 1)$ へ reshape する.
- $(N,C, H, W)$ の形状の画像データに加算する.
5. ガイダンス
5.0. シンプルな実装
- $y$ が最悪無視されて学習が行われる可能性がある.
- $y$ はラベルやテキストなどの画像の付加情報.
5.1. ノイズ $\epsilon$ を推定するモデルから, スコア $s$ を推定するモデルへ
\epsilon \approx -\sqrt{1-\bar{\alpha}_t} \color{red}{\boxed{\nabla_{x_t}{\log{p(x_t)}}}}
と近似できる (証明は省略)
スコアベースモデル
対数尤度関数の $x_t$ についての微分を スコア関数 (スコア) という.
ノイズではなく, スコア関数を推定するモデルも設計できる.
尤度ベースモデル
(VAE やいままで考えてきた DDPM などの) 対数尤度を最大化するモデル.
5.2. 分類器ガイダンス
![]()
5.3. 分類器なしガイダンス
![]()