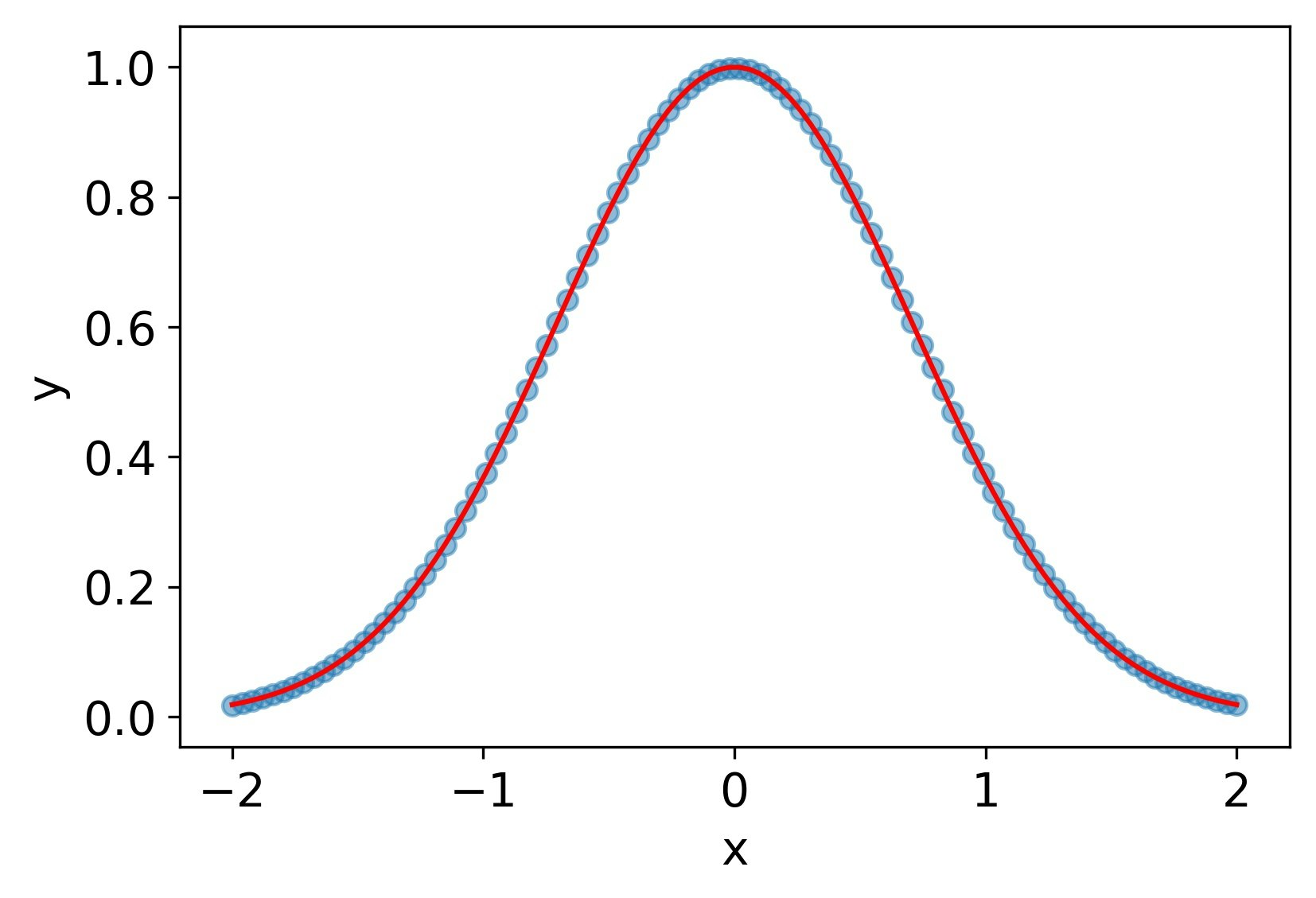
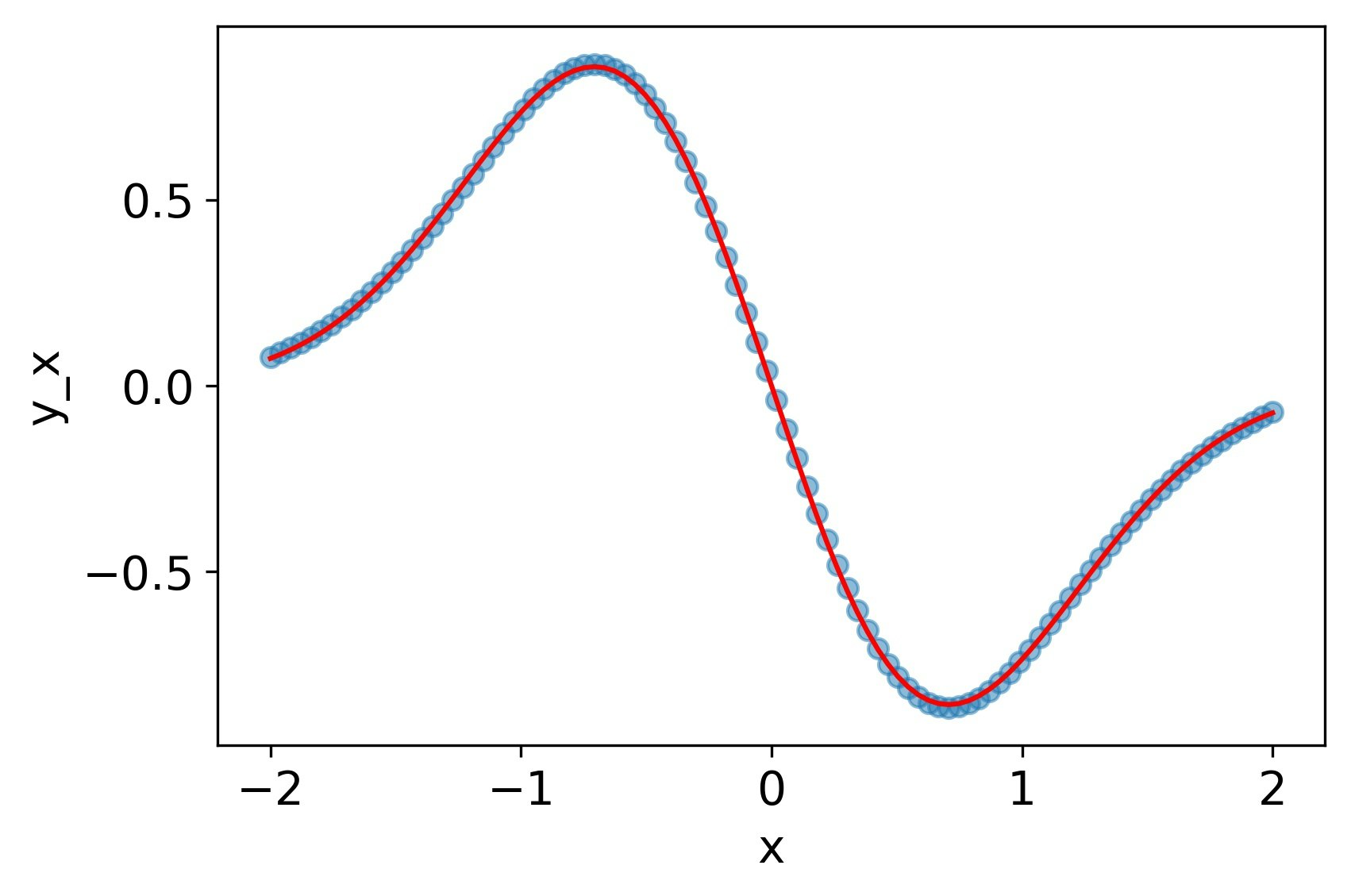
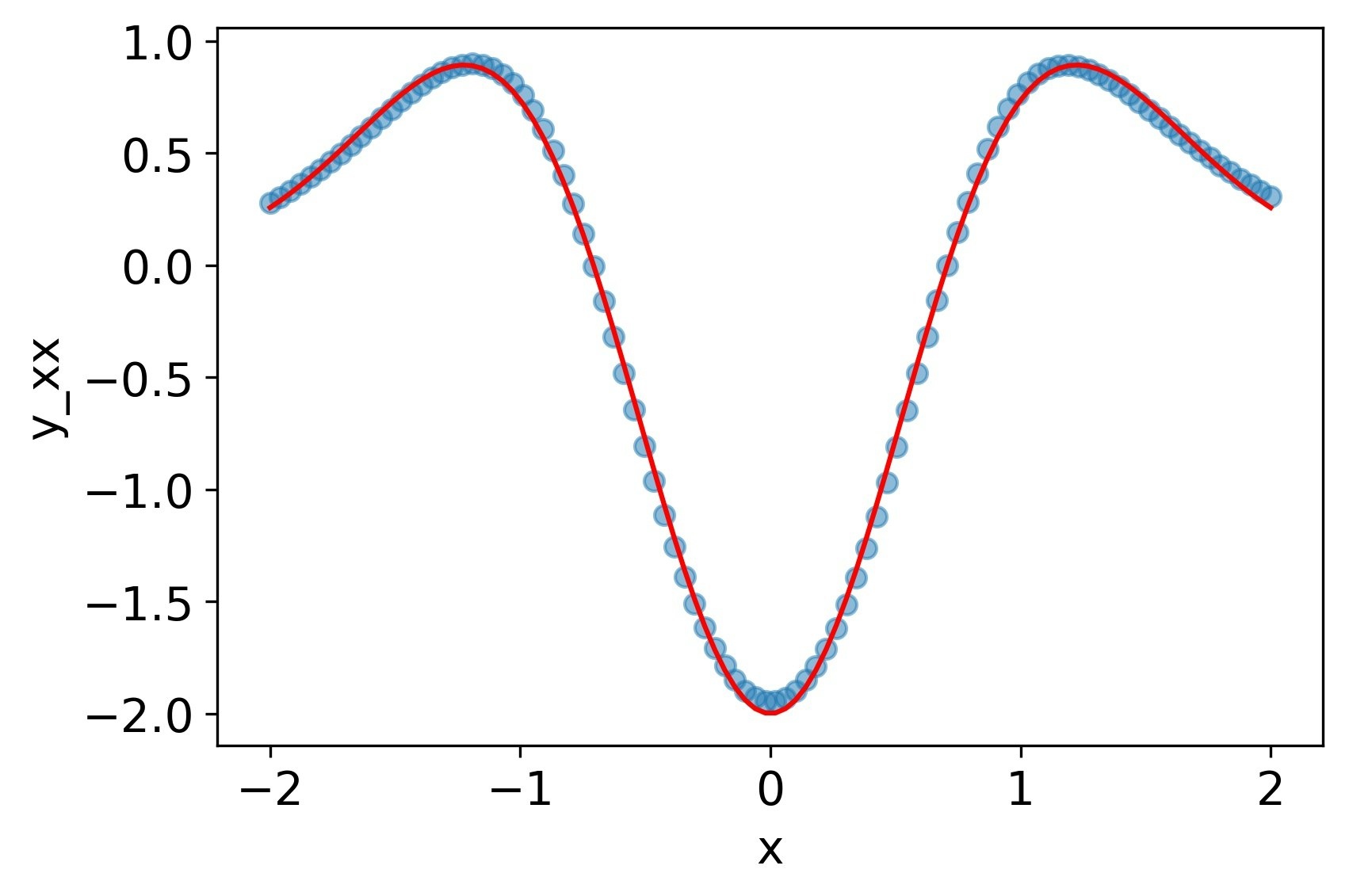
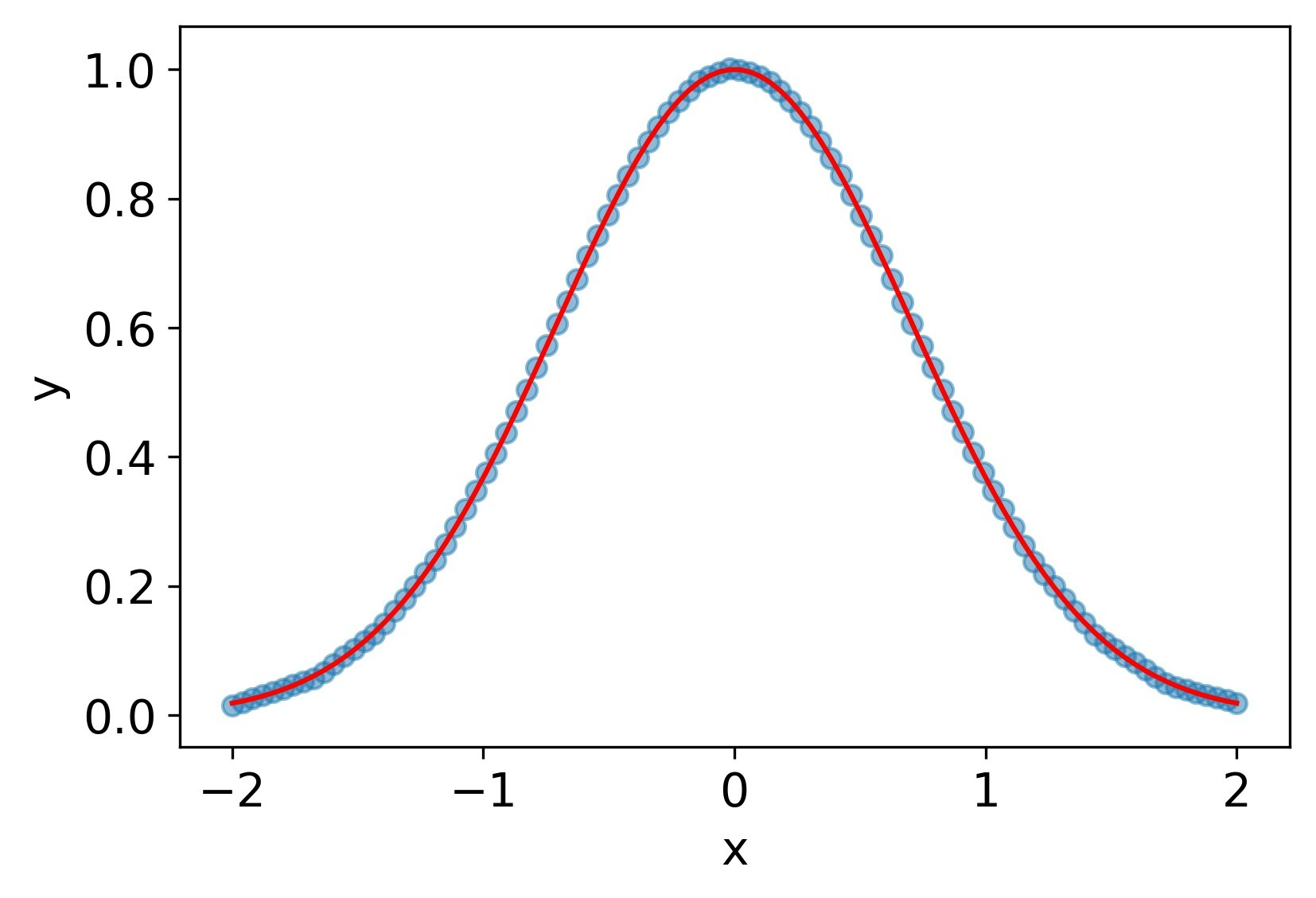
TL;DR
ニューラルネット出力の二階微分使いたいなら活性化関数はtanhかsoftplusにしよう。
はじめに
ニューラルネットの学習にweightやbiasの微分が使われているのは言うまでもない。これらが定義できるためには活性化関数が微分可能である必要がある。しかし、この要求は1階の微分に対してだけであり、2階以上の微分は要求されてない。2階以上の微分の情報が欲しいマニアックな場合は、それがうまく定義できている必要があるため、いつも使っている活性化関数が適切なのか検討する必要がある。
問題設定
1次元ガウス関数の回帰問題を考える。ガウス関数は
$$
y=e^{-x^2}
$$
であり、その1階微分、2階微分は次のようになる。
$$
\frac{dy}{dx}=-2xe^{-x^2}\\
\frac{d^2y}{dx^2}=(4x^2-x)e^{-x^2}
$$
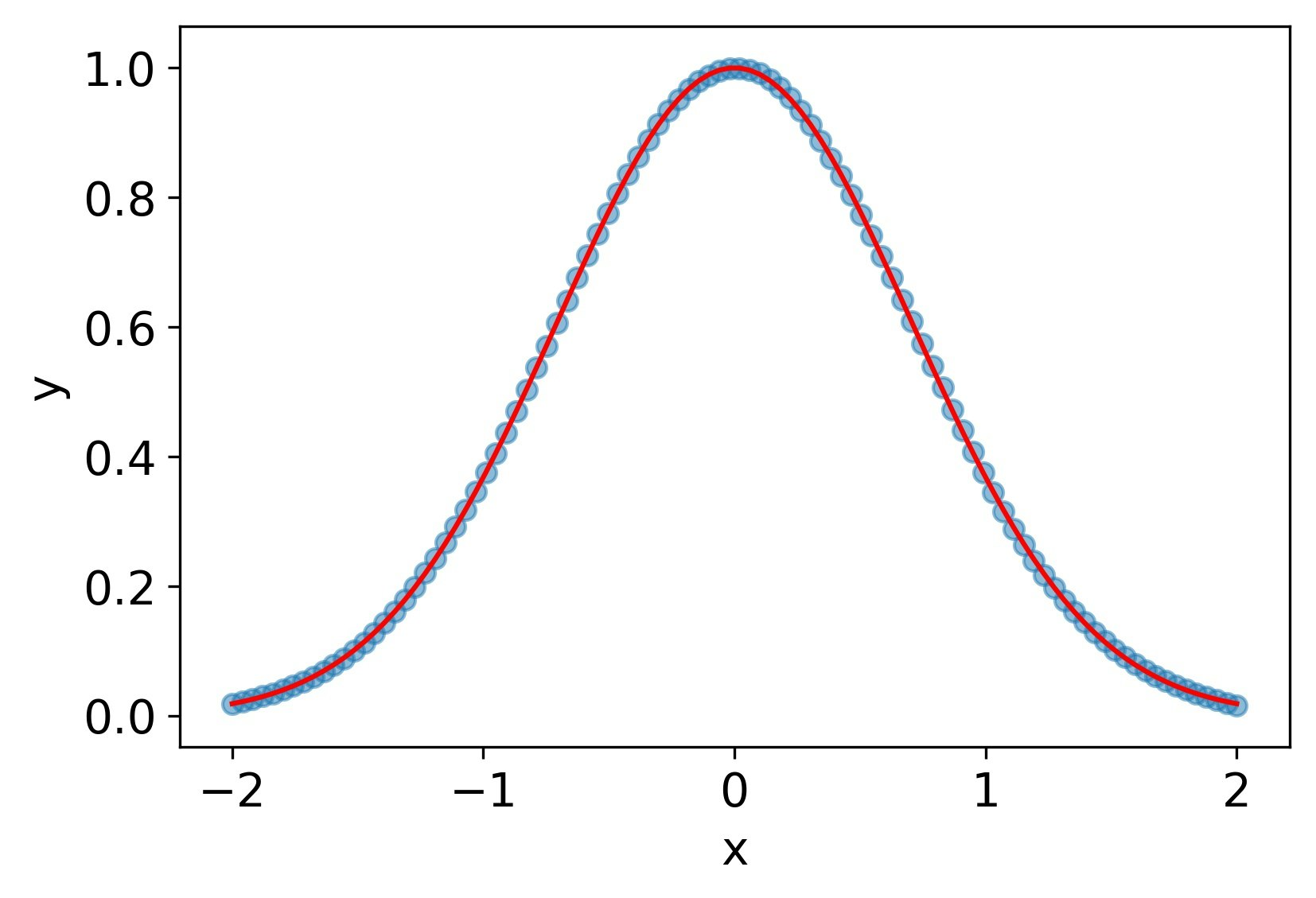
これらが正しく求められているかを評価する。ネットワークは隠れ層8層、各隠れ層のノード数20の全結合ネットワークを用いる。学習にはフルバッチのBFGSを用いる。教師データは$x\in[-2, 2]$のデータをランダムに1000点与える。また、テスト用データは$x\in[-2, 2]$を100分割した値を用いる。
結果
活性化関数はReLu
$$
\sigma(x)=\max(x,0)
$$
tanh
$$
\sigma(x)=\tanh(x)
$$
シグモイド関数
$$
\sigma(x)=\frac{1}{1+e^{-x}}
$$
softplus
$$
\sigma(x)=\log(1+e^x)
$$
selu
$$
\sigma(x)=\lambda
\begin{cases}
x & x>0\\
\alpha(e^x-1) &x\leq0
\end{cases}
$$
elu
$$
\sigma(x)=
\begin{cases}
x & x>0\\
\alpha(e^x-1) &x\leq0
\end{cases}
$$
を試す。
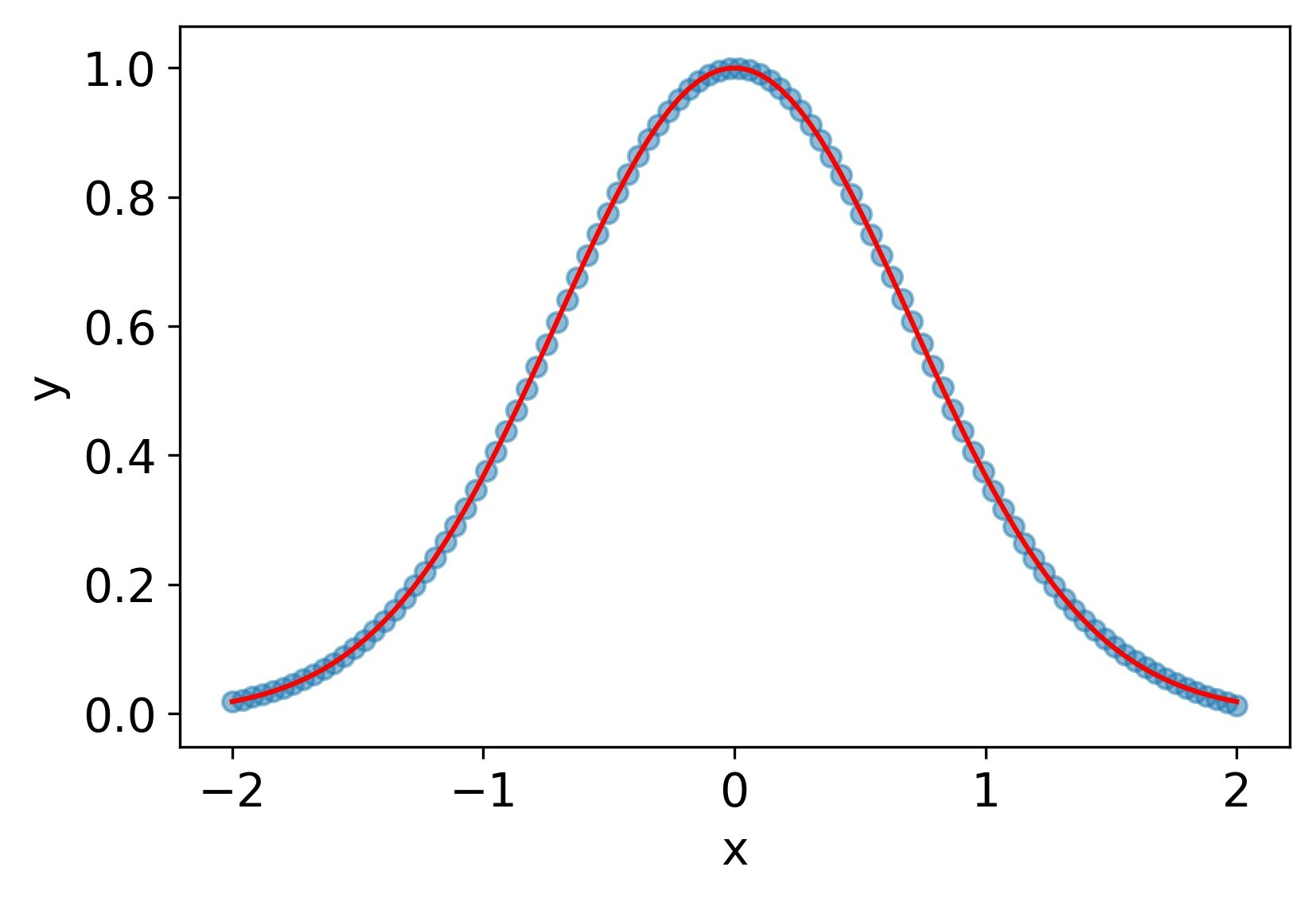
ReLU
関数自体は再現できているが、その微分は概形のみしか再現できていない。二階微分に至ってはすべて0になっている。
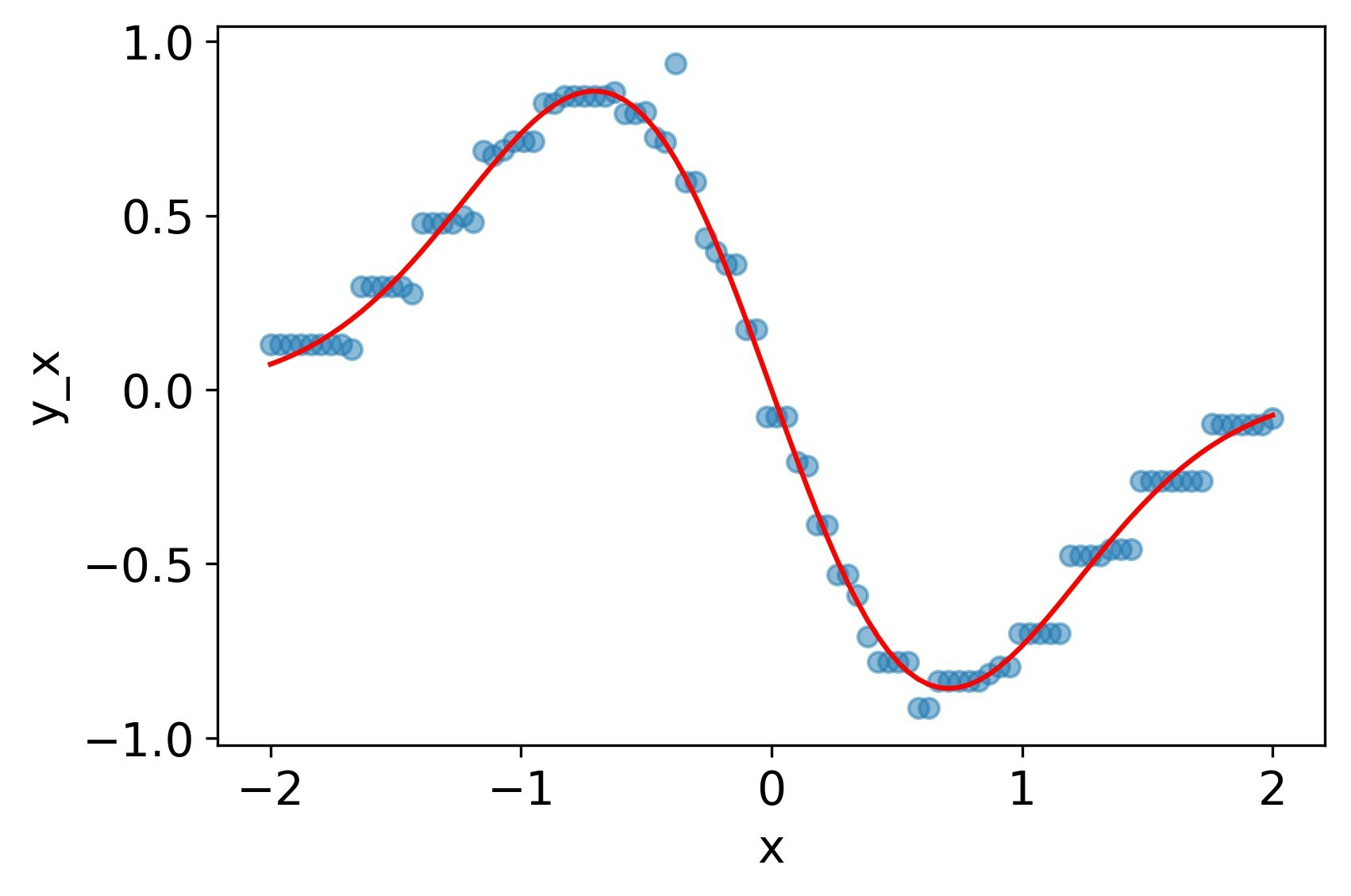
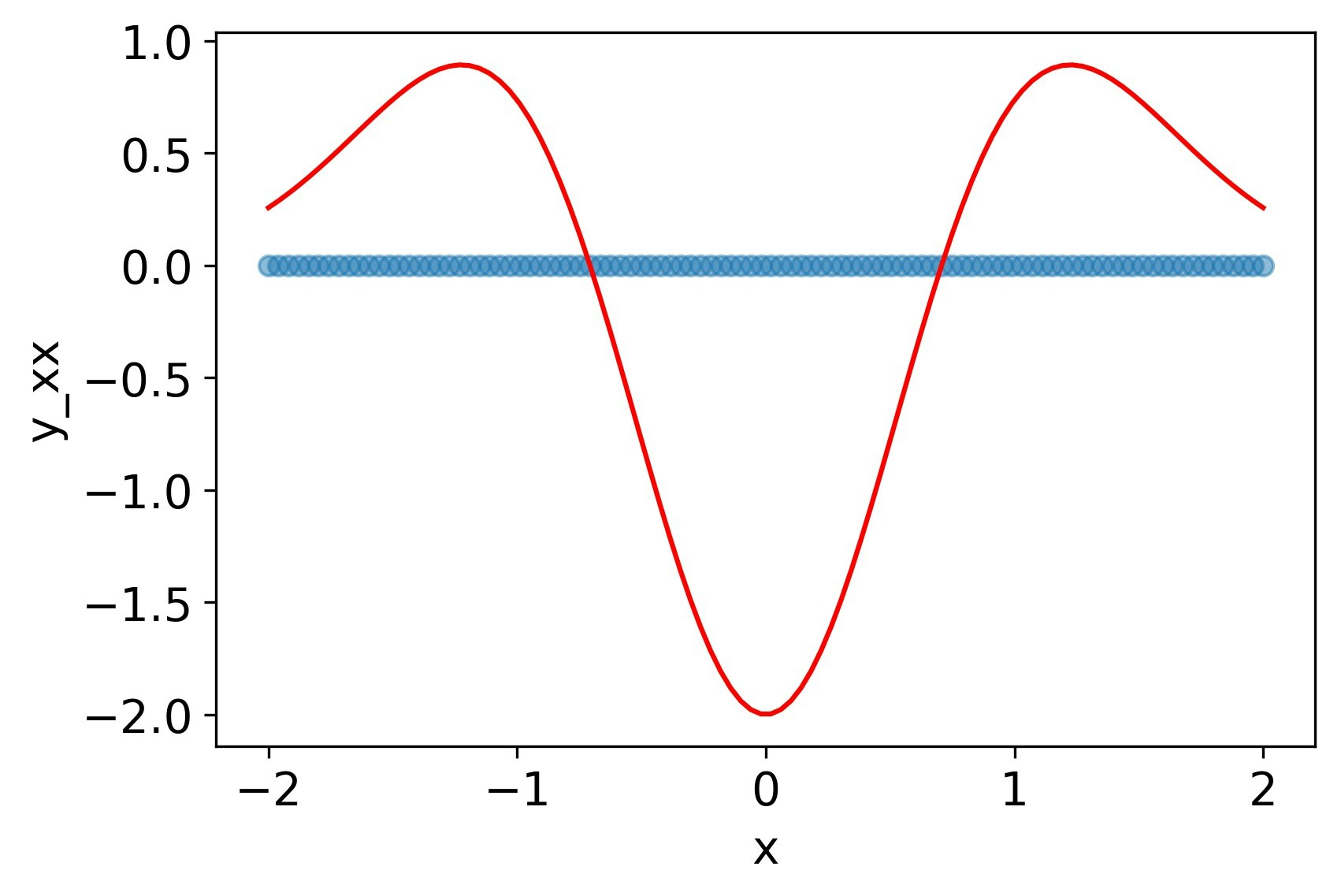
MSE誤差
| $y$ | $y_x$ | $y_{xx}$ |
|---|---|---|
| 1.4e-3 | 5.2e-2 | 9.6e-1 |
tanh
| $y$ | $y_x$ | $y_{xx}$ |
|---|---|---|
| 7.5e-4 | 4.8e-3 | 3.0e-2 |
シグモイド関数
なぜかBFGSがうまくいかなかったのでAdamで学習した。一回微分、二階微分ともにそこそこ再現できているが、tanhには劣る。
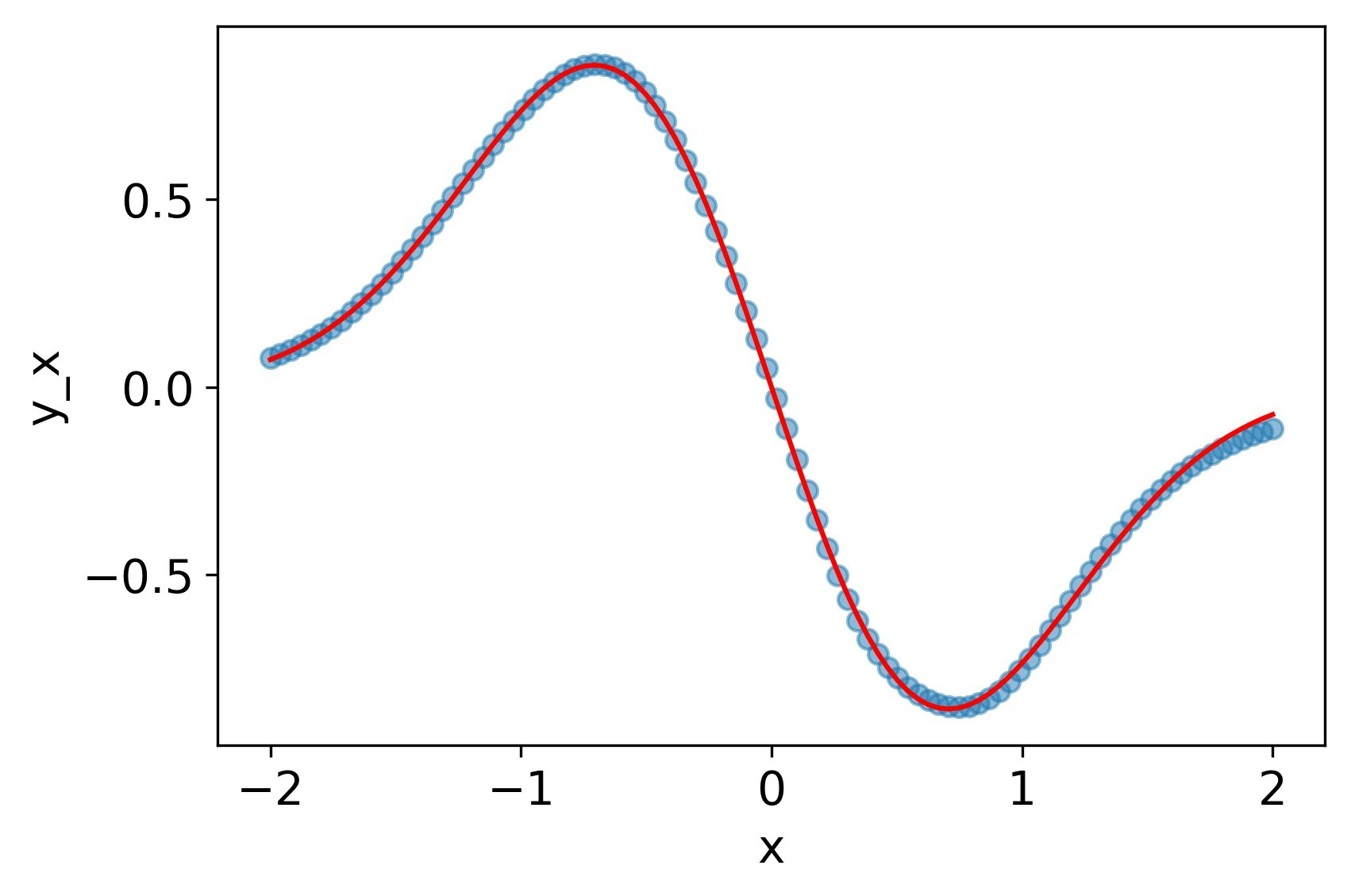

MSE誤差
| $y$ | $y_x$ | $y_{xx}$ |
|---|---|---|
| 1.2e-3 | 1.0e-2 | 6.6e-2 |
softplus
tanhと同じく、一回微分、二階微分ともによく再現できている。
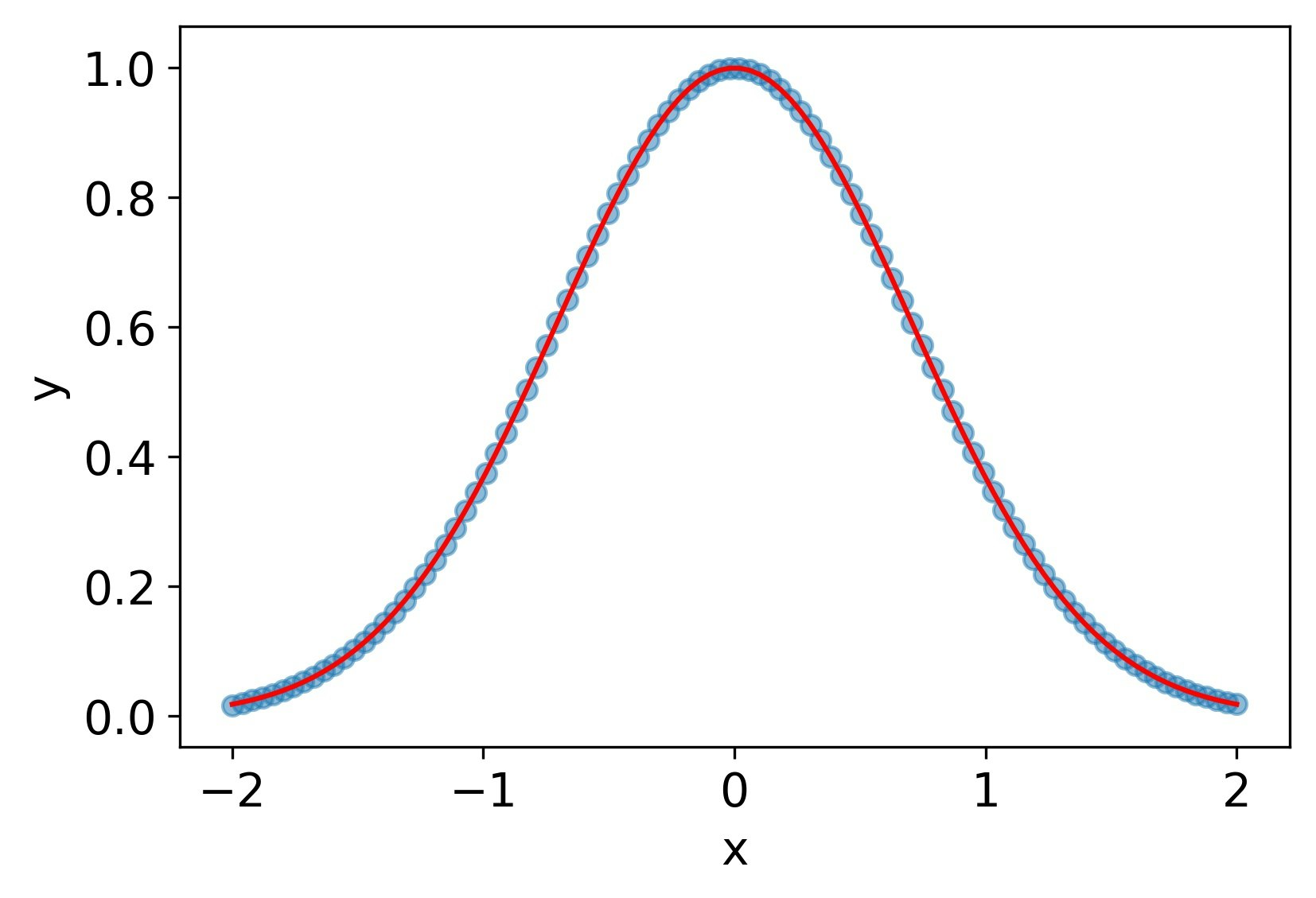
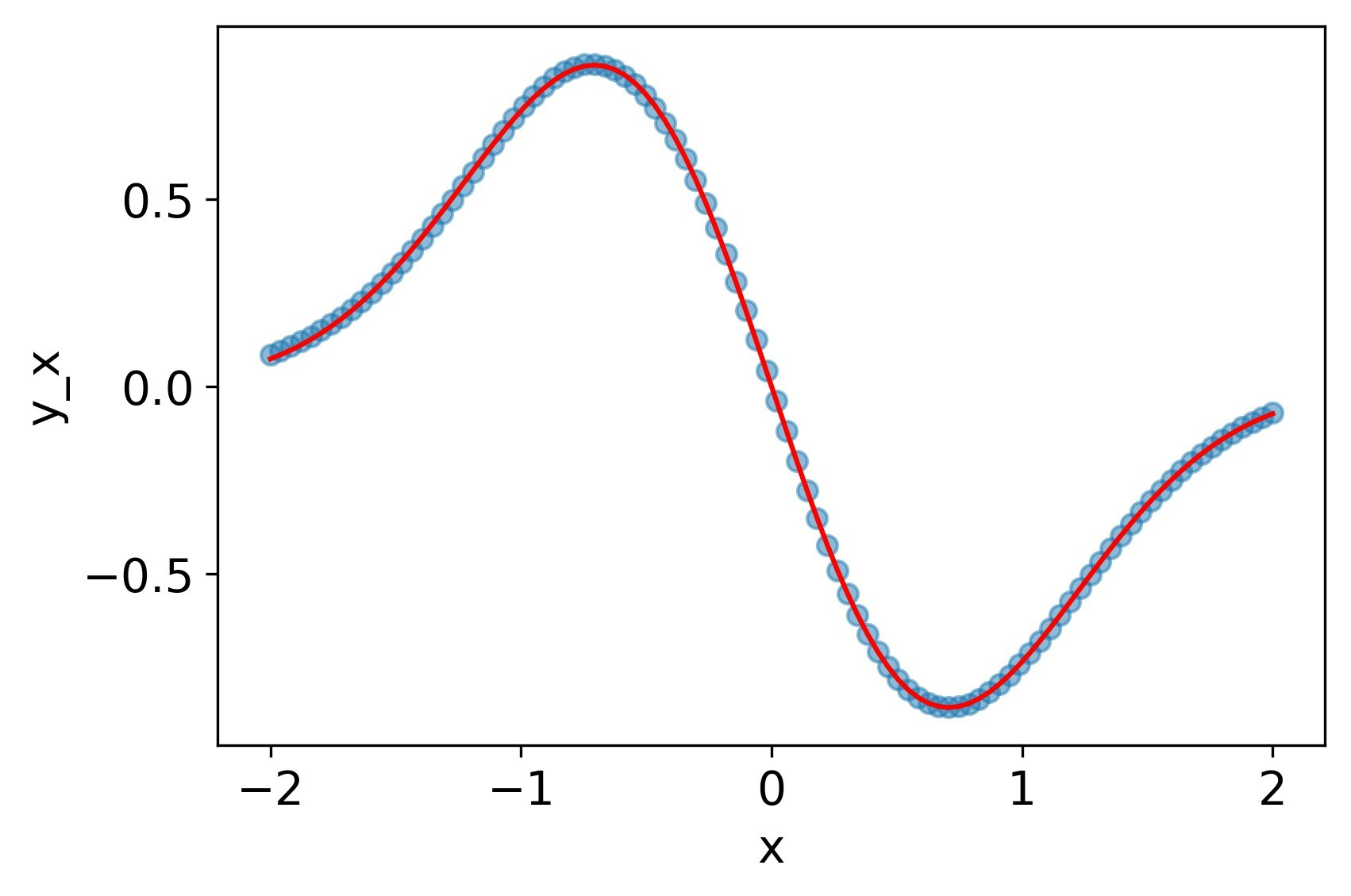
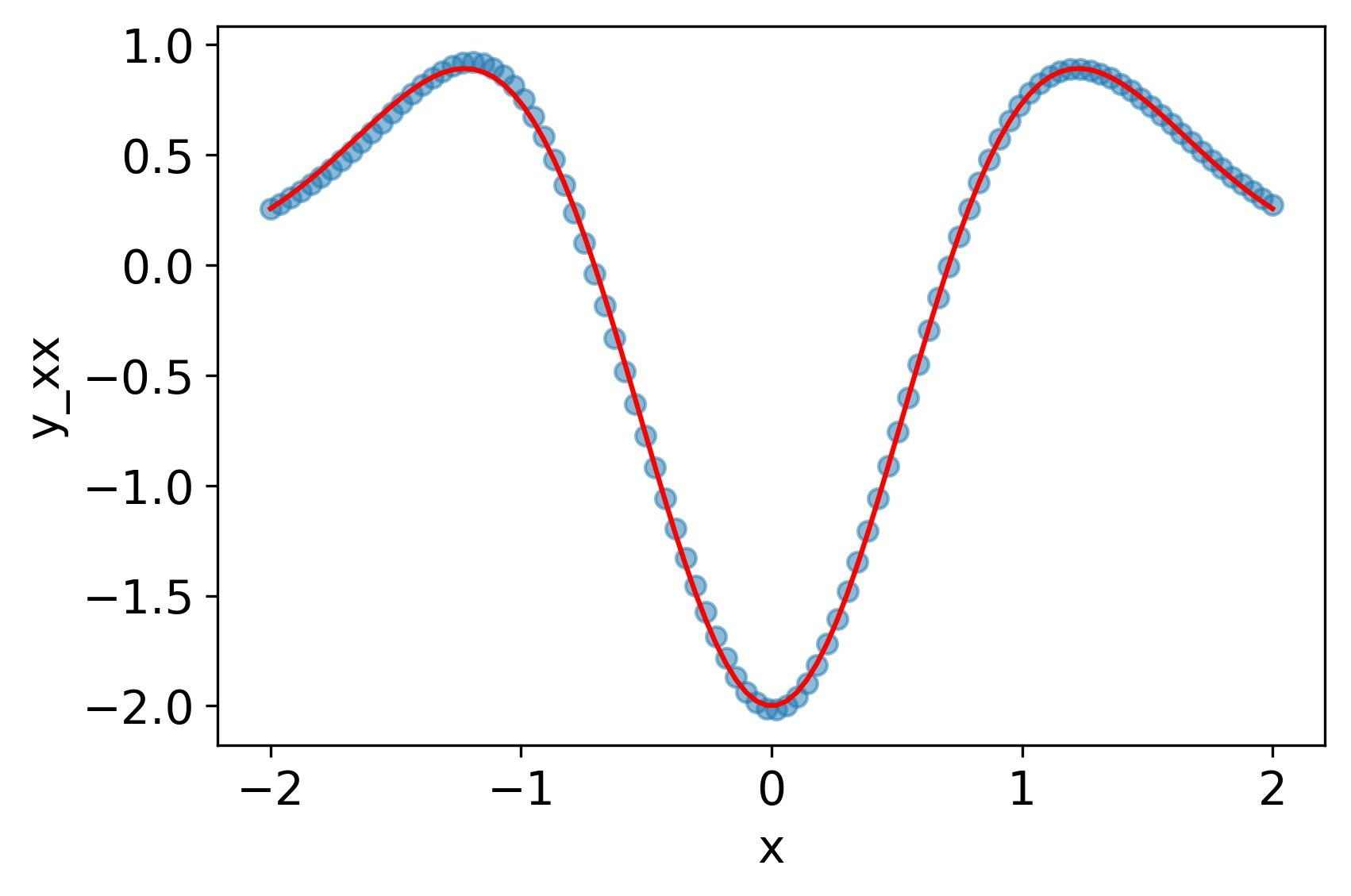
MSE誤差
| $y$ | $y_x$ | $y_{xx}$ |
|---|---|---|
| 4.7e-4 | 3.5e-3 | 2.0e-2 |
selu
一回微分はReLUよりマシだが、2階微分はダメダメ。
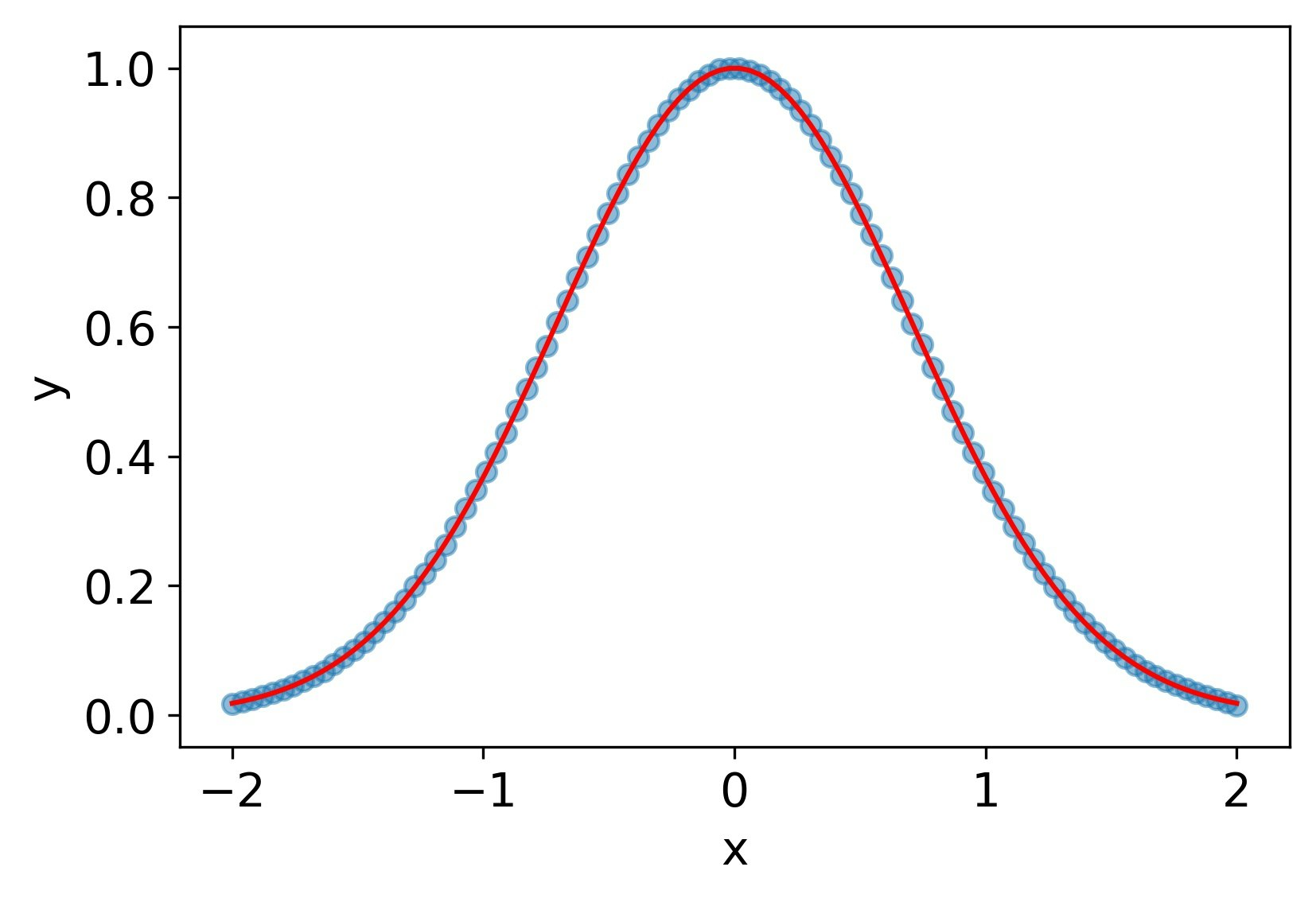
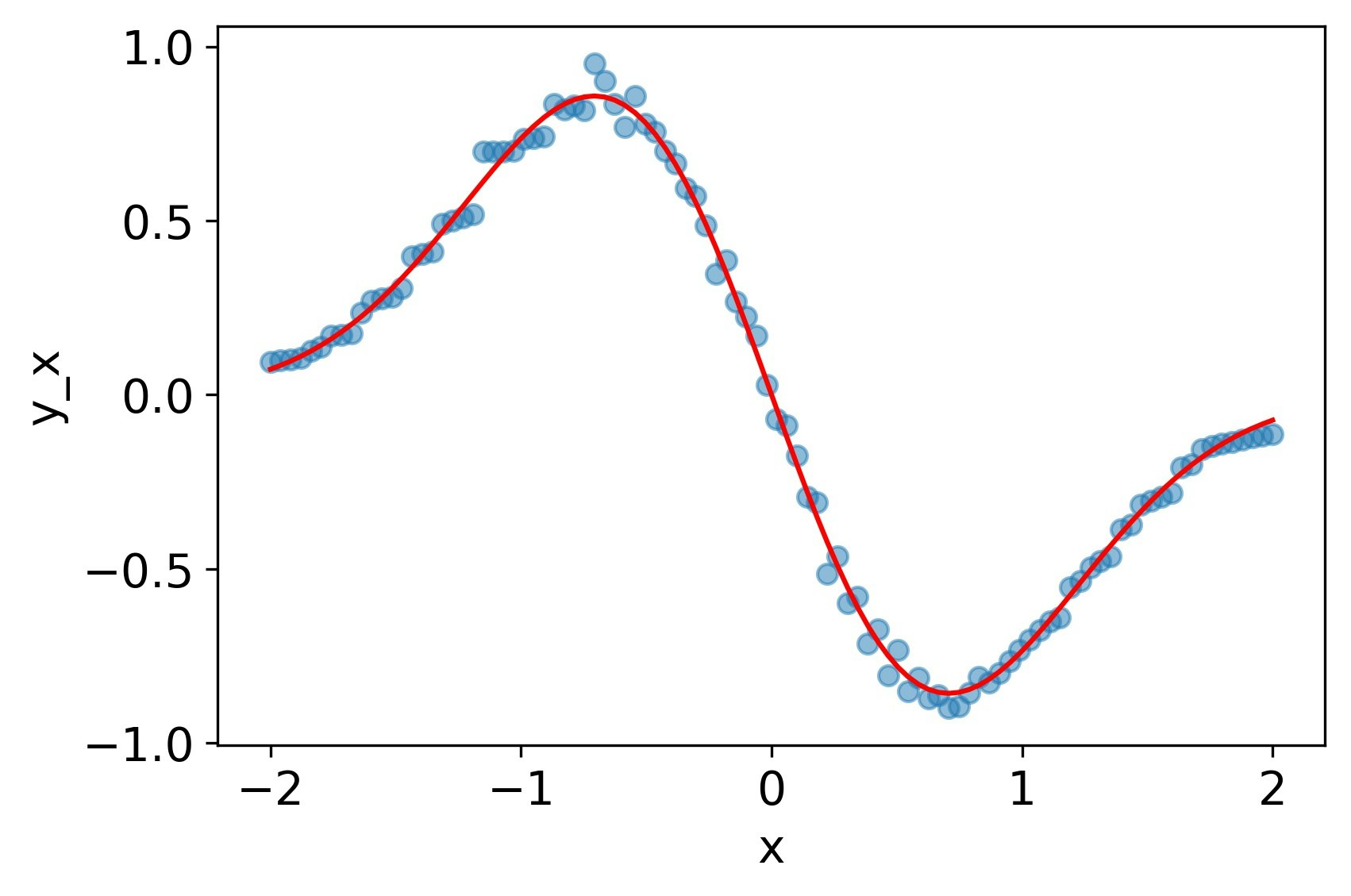

MSE誤差
| $y$ | $y_x$ | $y_{xx}$ |
|---|---|---|
| 7.7e-4 | 3.1e-2 | 1.9e+0 |
elu
一回微分まではそこそこだが、2階微分は可能性を感じるものの、残念な感じ。
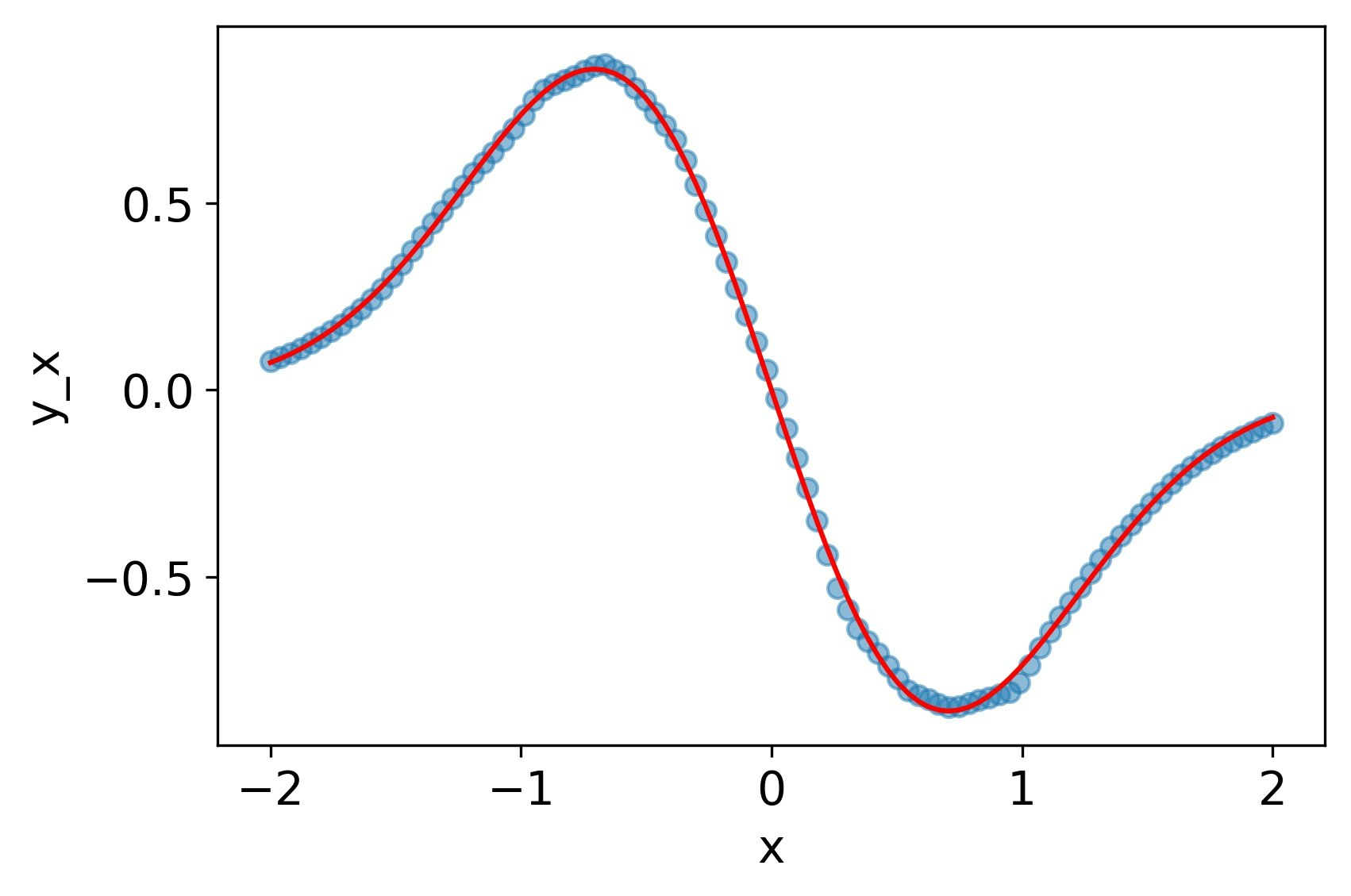
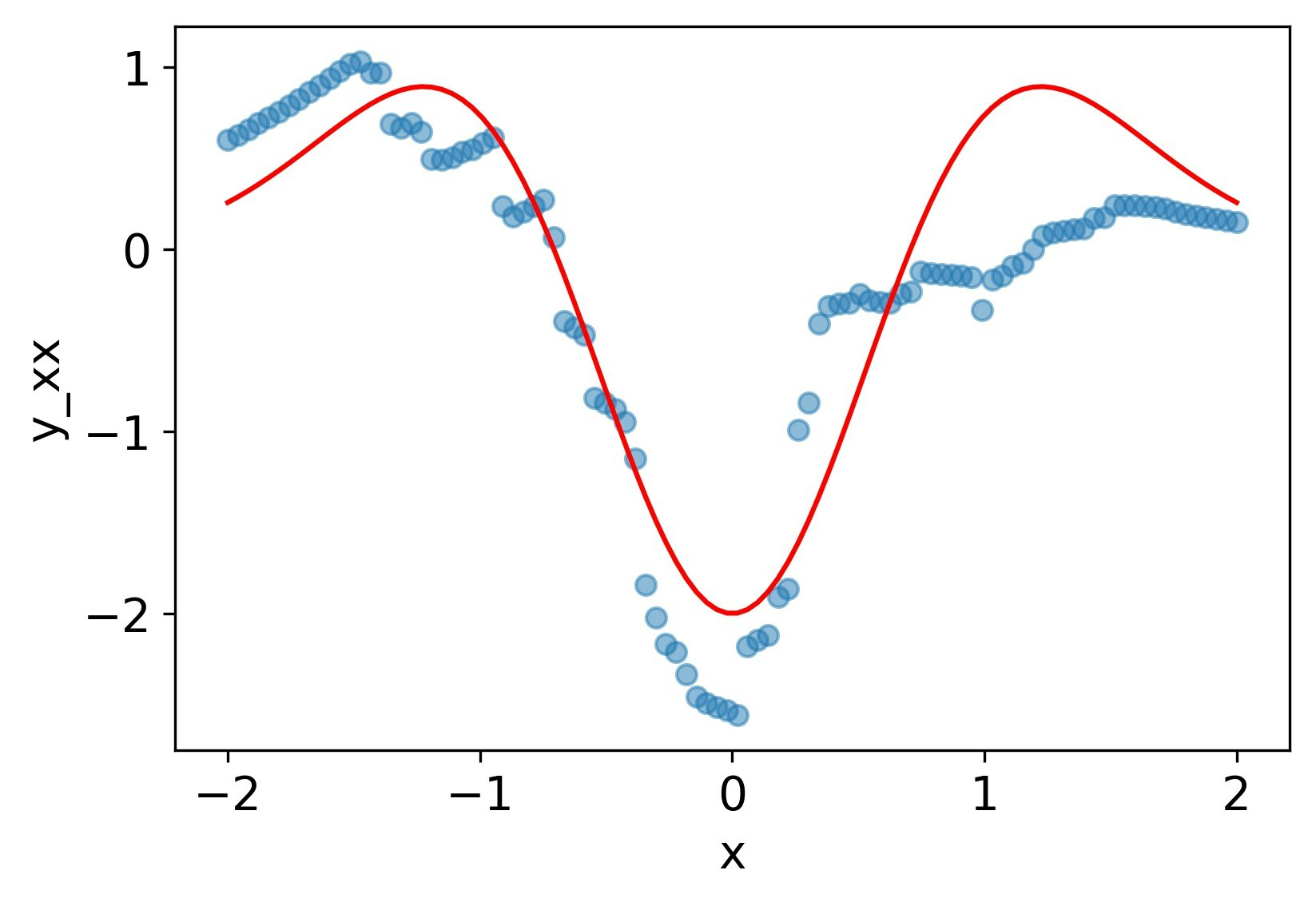
MSE誤差
| $y$ | $y_x$ | $y_{xx}$ |
|---|---|---|
| 1.2e-3 | 1.3e-2 | 4.7e-1 |
MSE誤差をまとめる次のようになる。
| 活性化関数 | $y$ | $y_x$ | $y_{xx}$ |
|---|---|---|---|
| ReLU | 1.4e-3 | 5.2e-2 | 9.6e-1 |
| tanh | 7.5e-4 | 4.8e-3 | 3.0e-2 |
| シグモイド関数 | 1.2e-3 | 1.0e-2 | 6.6e-2 |
| softplus | 4.7e-4 | 3.5e-3 | 2.0e-2 |
| selu | 7.7e-4 | 3.1e-2 | 1.9e+0 |
| elu | 1.2e-3 | 1.3e-2 | 4.7e-1 |
考察
ReLUがうまくいかない理由は、そもそも(原点を除いて)二階微分が0になるからである。eluやseluは、負の値に関しては二階以上の微分可能であるものの、正の値ではReLUと同様、二階微分が0になるため、うまくいかないと考えられる。tanhやシグモイド関数、softplusはすべての領域に渡って二階以上の微分が可能であるため、うまくいっている考えられる。ただし、シグモイド関数が若干劣っている意味はよくわからない。何かアイデアがあれば教えていただきたい。
結論
ニューラルネット出力の二階微分使いたいなら活性化関数はtanhかsoftplusにしよう。
参考
二階以上の微分が必要な場合としては、BFGSのような二階微分の情報を使った学習アルゴリズムなどがある。とはいっても、2階微分が0でも1階微分が有限であれば学習が進むため、ReLUでもBFGSは使える。他には、ディープラーニングで微分方程式を解く場合は2階以上の微分が必要となる(拙作の理論編、実践編)。