概要
最近、ディープラーニングで微分方程式が解けるという話を聞いたので、気になって調べてみた。この記事では2つの手法について概観をまとめる。なお、記法は原論文に従うので章ごとにばらばらになるがご容赦いただきたい。
はじめに
従来、解析的に解くことが難しい微分方程式はRunge-Kutta法などの反復解法を用いることで解かれてきた。これらの手法は陰で我々の生活を支えているといっても過言ではない。しかし、多次元になったときの困難さや、分割により本来的に離散的になるという問題点を抱えている。一方、近似関数を用いると連続的な解を得ることができるが、厳密性などは失われる。ニューラルネットはあらゆる関数を任意の精度で近似できるため、微分方程式の連続的な解が精度よく求められる可能性がある。
二層パーセプトロンでの近似
この手法はI. E. Lagarisらによって1998年に提案された手法である。二階の常微分方程式
$$
G(\vec{x},\Psi(\vec{x}),\nabla\Psi(\vec{x}),\nabla^2\Psi(\vec{x}))=0
$$
を考える。ここで、$\vec{x}=(x_1, \cdots,x_n)\in {\bf R}^n$は座標を、$\Psi(\vec{x})$は求めるべき解を表す。この解を二層パーセプトロンを含む試行関数$\Psi(\vec{x}, \vec{p})$で近似する場合($\vec{p}$はネットワークのパラメータ)、求めるべきは
$$
\sum_{\vec{x}_i\in{\bf R}^n}(G(\vec{x}_i,\Psi(\vec{x}_i),\nabla\Psi(\vec{x} _i),\nabla^2\Psi(\vec{x} _i)))^2
$$
を最小化する$\vec{p}$となる。試行関数は境界条件や初期条件を満たすようにとる。
$$
\Psi(\vec{x})=A(\vec{x})+F(\vec{x},N(\vec{x},\vec{p}))
$$
ここで、$A(\vec{x})$は境界条件などを表し、$N(\vec{x},\vec{p})$は入力数$n$、出力数$1$の二層パーセプトロンを表す。$F$は境界で第二項が0になるように選ぶ。当然ながら、中間層のノード数は関数を十分近似できるだけ大きくとらなければならない。学習はBFGS法や勾配降下法を用いて行う。具体的なコーディングはこの記事によくまとまっている。他の論文にラプラス方程式を解いたきれいな絵があるので掲載する。厳密解との誤差は大きくても$10^{-4}$オーダーであり、十分実用的な精度といえる。
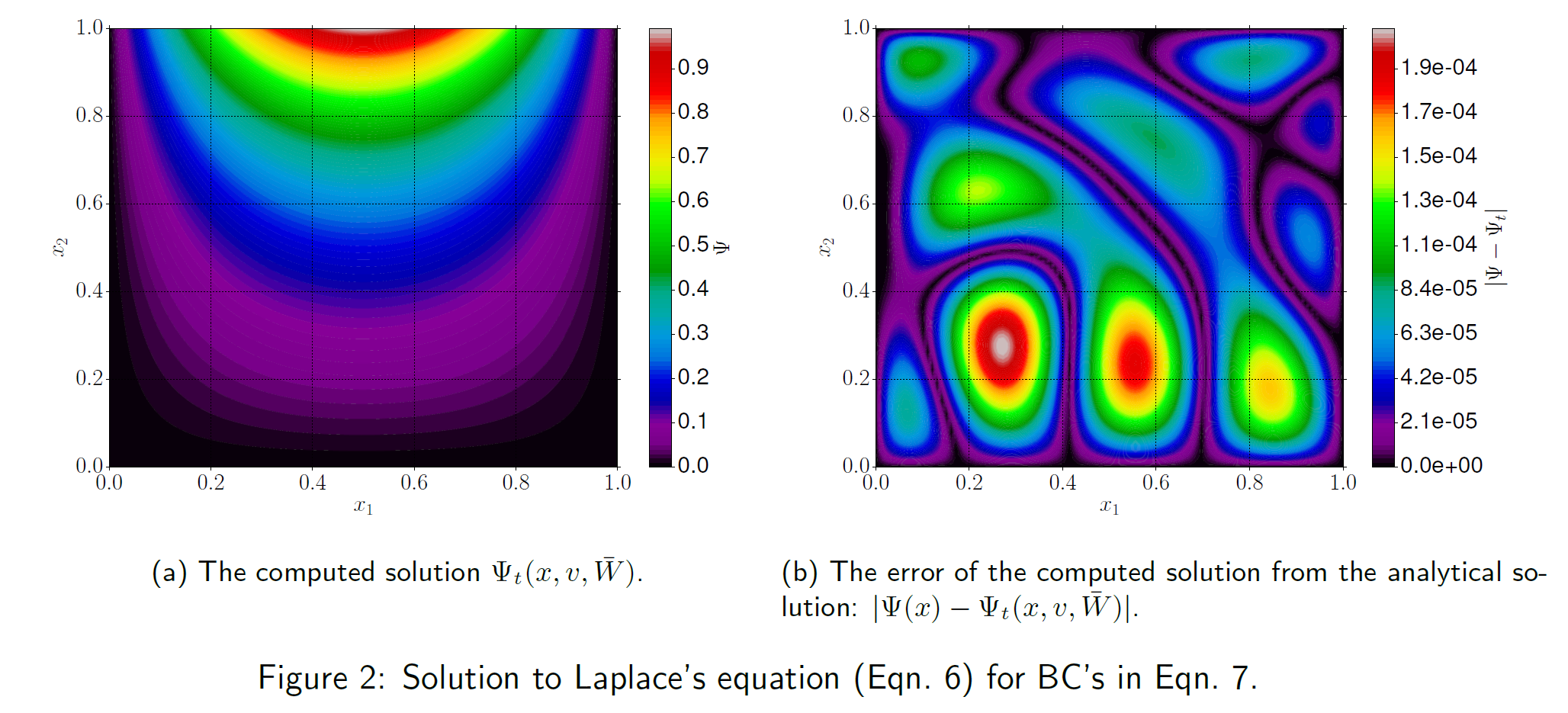
Solving differential equations using neural networks, M. M. Chiaramonte and M. Kiener, 2013より引用
Data-driven solution
この手法は2017年にM. Raissiらによって提案された手法である。連続時間法と離散時間法の二種類がある。
連続時間法
解きたい微分方程式を
$$
u_t+{\mathcal N}[u]=0
$$
と表す。ここで$u(t, x)$は求めるべき解、${\mathcal N}[\bullet]$は空間微分などを含む演算子である。$x\in\Omega$は${\bf R}^d$上の部分空間を、$t\in[0,T]$は時間を表す。下付き文字は偏微分を表す。上式の右辺を
$$
f:=u_t+{\mathcal N}[u]
$$
と定義し、$u$をディープニューラルネットで近似することを考える。損失関数は二乗誤差
$$
MSE=MSE_u+MSE_f
$$
とする。ここで、
$$
\begin{align}
MSE_u&=\frac{1}{N_u}\sum_{i=1}^{N_u}|u(t_u^i,x_u^i)-u^i|^2 \\
MSE_f&=\frac{1}{N_f}\sum_{i=1}^{N_f}|f(t_f^i,t_f^i)|^2
\end{align}
$$
はそれぞれ拘束条件(初期条件や境界条件)に関する誤差、微分方程式そのものに関する誤差である。拘束条件が式で与えられている場合(時間反転対称性など)は、別途該当する二乗誤差の項を追加すればよい。$\{t_u^i,x_u^i,u_i\}_{i=1}^{N _u}$は拘束条件の訓練データ、$\{t _f^i,x _f^i\} _{i=1}^{N _f}$は微分方程式そのものに対する訓練データである。これを最小化することで微分方程式の近似解を得る。この手法のポイントは、
- 拘束条件をハードコーディングしないため、複雑な条件の設定が可能である
- 拘束条件以外のデータを用いる必要がない
- 第二項により全体が微分方程式に従うようになる
である。これにより1次元burger's方程式を解いた図を次に示す。黒い×は初期条件と境界条件として与えたサンプル点である。各時刻において、厳密解とよく一致していることが分かる。
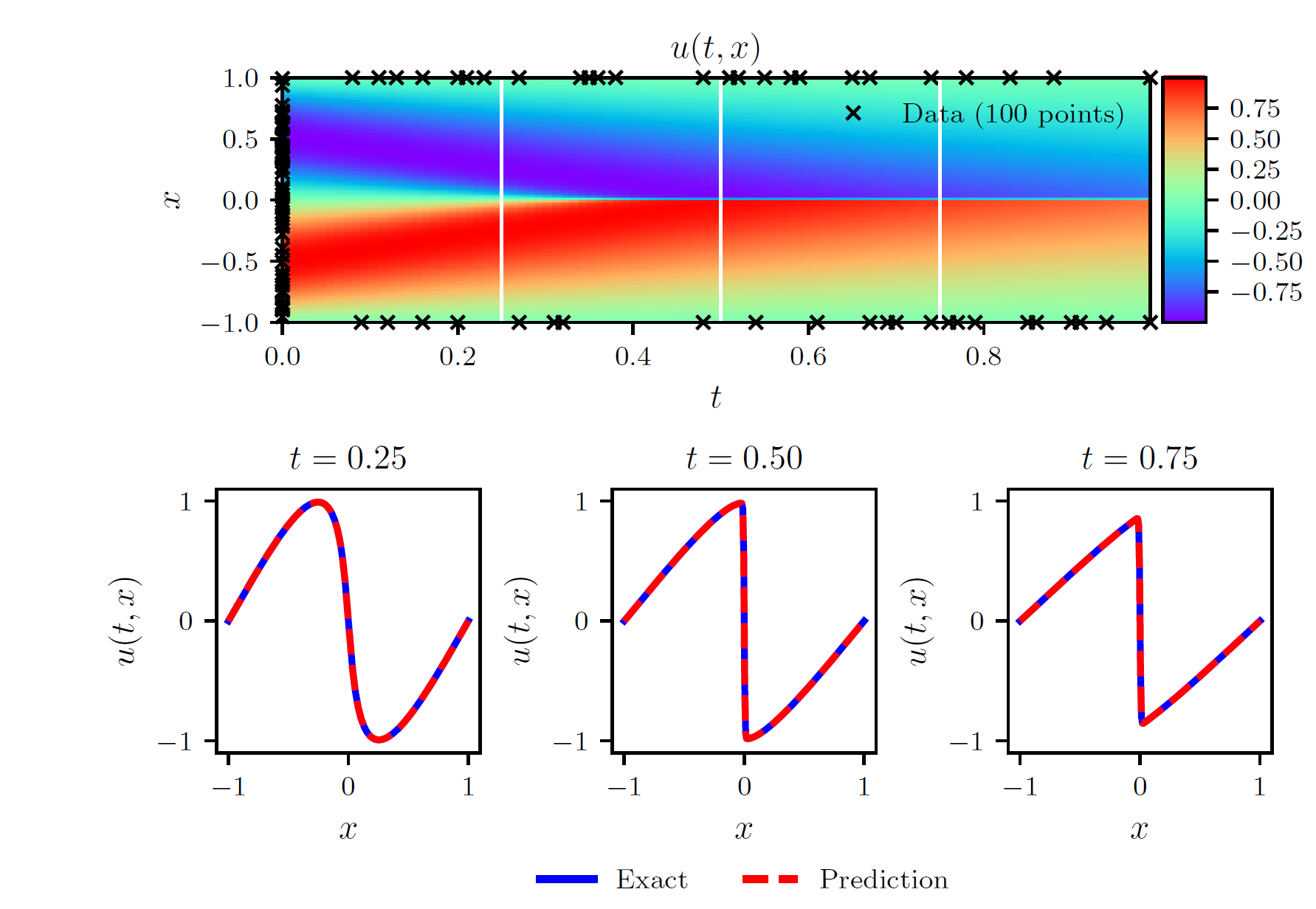
M. Raissi et al., arXiv:1708.07469 [q-fin.MF]より引用
離散時間法
上記の方法では$N_f$は次元が増えると指数関数的に増えるため、3次元以上の問題を扱う場合はその数が問題になってくる。そこで、時間方向の次元のサンプリングをしなくて済むようにする方法が離散時間法である。 離散時間法は時間発展にRunge-Kutta法を用いることで$N_f$を減らすことができる。Runge-Kutta法の次数を大きく(16など)すれば、時間刻みはそこまで細かくなくても精度の良い近似解が得られる。
結論
ディープラーニングを用いることで微分方程式の微分可能な近似解が精度よく求まる。今回調べた論文では教師あり学習で、かつ単純な全結合ネットを用いていたが、LSTMのようなRNNを用いることで精度が上がるという報告や、強化学習を使って近似解を求めるという研究もあり、まだまだ発展途上の分野であると感じた。そのうち自分で実装してみたい。