はじめに
微分方程式の数値的な解法にもいろいろあるが、その中にディープラーニングで微分方程式を解くという手法がある。手法自体は1990年代から提案されていたが、最近になっていろいろな論文が出始めてきた。ただ、やっぱり使ってみないとわからないので、本記事では簡単な問題に適用し、その効能を探ってみようと思う。前の記事で手法についての簡単なレビューを行っているので、興味のある方はご一読いただきたい。
ニューラルネットによる解法の利点
ニューラルネットによる解法の利点のひとつは、滑らかな解が得られることである。通常の数値計算であれば、シミュレートした点以外の点の答えを求めようとする場合、内挿処理などを行う必要がある。しかし、ニューラルネットによる解法では、各点の値ではなく、関数そのものが解として得られるため、内挿処理の必要はない。また、解の微分が高精度で得られることも大きなアドバンテージである。
また、メッシュフリーであることも利点であるといえる。メッシュベースの数値計算の大きな制約の1つは、高次元(e.g. 空間3次元+時間1次元)で計算が困難となることである。一方、ニューラルネットによる解法は高次元空間内のランダムな点を利用することでメッシュによる制約を取り払っている。これにより、空間次元や時間次元だけでなく、パラメータ次元も同時に表現するような解を得られる可能性がある(J. Sirignano and K. Spiliopoulos, arXive 1708.07469)。
問題設定
誰もが簡単にわかる問題としたいため、斜方投射を考えることにする。斜方投射はボールを投げた時の軌跡を求める問題である。この軌跡は、重力のみが働いている運動方程式の解として得られる。運動方程式
$$
m\frac{d^2{\bf r}}{dt^2}={\bf F}
$$
を考える。外力は重力のみなので
$$
{\bf F}=-mg\hat{z}
$$
である。ここで、$g=9.8[m/s^2]$は重力加速度である。これを運動方程式に代入して質量$m$を消去すると
$$
\frac{d^2{\bf r}}{dt^2}=-g\hat{z}
$$
が得られる。この解は単純に積分するだけで求められる。$x$-$z$平面の運動のみに着目すると、
$$
x(t)=x_0+v_{0x}t\\
z(t)=z_0+v_{0z}t-\frac{1}{2}gt^2
$$
となる。ここで、$(x_0,z_0)$は初期位置、$(v_{0x},v_{0z})$は初速度である。当然、この解は答えを確かめるときにのみ用いる。この微分方程式を解くためには、4つの境界条件が必要となる。境界条件の与え方はなんでもよいが、ここではシンプルに初期位置と初速度を与える。初期位置は平行移動のみであり、変えても面白くないので、原点$(0,0)$に固定することとする。
解法
微分方程式の解法はM. Raissiらによって提案された手法をベースに用いる。この手法では、解を多層のニューラルネットワークで表し、微分方程式に従うと0になるような損失関数と、解が境界条件に従うと0になるような損失関数を足し合わせて、それを最小化することで解を求める。$(x(t),z(t))$のニューラルネットワークによる近似解を$(\tilde{x}(t),\tilde{z}(t))$とする。
ネットワーク構成
M. Rassi et al.に従い、中間層8層、中間層のノード数20、活性化関数tanhのネットワークを用いる。入力は時間に加え、初速度$(v_{0x},v_{0z})$も与える。出力は$(\tilde{x},\tilde{z})$の二次元である。これにより、初速度に関してもパラメトリックな関数$(\tilde{x}(t,v_{0x},v_{0z}),\tilde{z}(t,v_{0x},v_{0z}))$を得る。なお、学習時はフルバッチのL-BFGS法を用いる。
損失関数
本記事の問題設定において、微分方程式に関する損失関数は
$$
MSE_{x}=\sum_i\left|\frac{\partial^2\tilde{x}(t^i,v_{0x}^i,v_{0z}^i)}{\partial t^2}\right|^2\\
MSE_{z}=\sum_i\left|\frac{\partial^2\tilde{z}(t^i,v_{0x}^i,v_{0z}^i)}{\partial t^2}+g\right|^2
$$
で与えられる。境界条件に関する損失は、初期位置に関して
$$
MSE_{x_0}=\sum_i\left|\tilde{x}(t^i,v_{0x}^i,v_{0z}^i)-x_0\right|^2\\
MSE_{z_0}=\sum_i\left|\tilde{z}(t^i,v_{0x}^i,v_{0z}^i)-z_0\right|^2
$$
初速度に関して
$$
MSE_{v_{0x}}=\sum_i\left|\frac{\partial\tilde{x}(0,v_{0x}^i,v_{0z}^i)}{\partial t}-v_{0x}^i\right|^2\\
MSE_{v_{0z}}=\sum_i\left|\frac{\partial\tilde{z}(0,v_{0x}^i,v_{0z}^i)}{\partial t}-v_{0z}^i\right|^2
$$
となる。全体の損失関数は、これらすべてを足し合わせた
$$
MSE=MSE_x+MSE_z+MSE_{x_0}+MSE_{z_0}+MSE_{v_{0x}}+MSE_{v_{0z}}
$$
となる。
結果
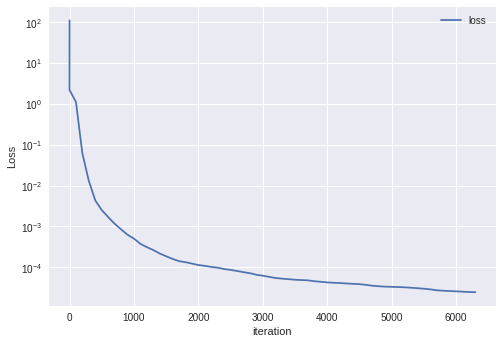
$t\in[0,1],v_{0x},v_{0z}\in[0,5]$として、$(t,v_{0x},v_{0z})$をランダムに1万点与えて学習させた。コードは長くなるので割愛する。興味のある方はgithubをご覧いただきたい。下図に損失関数のグラフを示す。損失関数の値はかなり小さいことが分かる。なお、学習時間はgoogle colaboratoryのGPUを使って5分程度である。
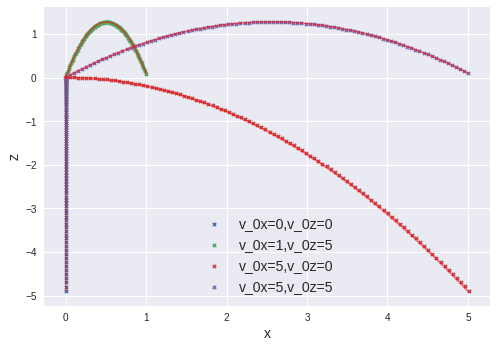
では、$(x,z)$の予測結果を見てみよう。下図に$t\in[0,1]$に対する予測結果を✖で示す。赤線は厳密解である。どの初期状態に対しても厳密解をよく再現していることが分かる。
エネルギー保存則
運動方程式に従う運動は全エネルギーが保存される。すなわち、運動エネルギー
$$
E_V=\frac{1}{2}m|{\bf v}|^2
$$
と位置エネルギー
$$
E_U=mgz
$$
の和が保存されるはずである。$(v_{0x},v_{0z})=(5,5)$の場合にこれらをプロットすると次の図のようになる。
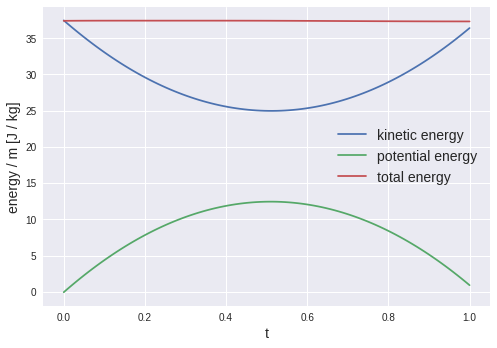
エネルギー保存則が綺麗に成り立っていることが分かる。運動エネルギーの計算には速度が入っており、得られた解の微分を計算する必要がある。通常の数値解法であれば、差分近似によりこれを評価するが、ディープラーニングを用いる手法では解の微分が直接計算できるため、通常の数値解法よりも精度のよい演算結果を得ることができる。
考察
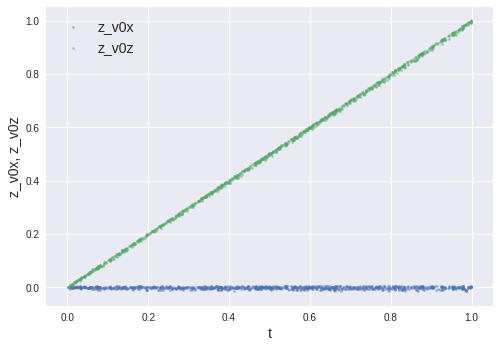
ネットワーク構成のところでさらっと$(\tilde{x}(t,v_{0x},v_{0z}),\tilde{z}(t,v_{0x},v_{0z}))$が得られると書いたが、厳密解を見ると$x$は$v_{0z}$には、$z$は$v_{0x}$には依存していない。この特徴を捉えられているかを確かめるため、$t\in[0,1],v_{0x},v_{0z}\in[0,5]$として$(t,v_{0x},v_{0z})$をランダムに生成し、学習した関数について
$$
\frac{\partial\tilde{x}}{\partial v_{0x}},~\frac{\partial\tilde{x}}{\partial v_{0z}}~,\frac{\partial\tilde{z}}{\partial v_{0x}}~,\frac{\partial\tilde{z}}{\partial v_{0z}}
$$
を計算してみる。期待する結果は当然、
$$
\frac{\partial\tilde{x}}{\partial v_{0x}}=\frac{\partial\tilde{z}}{\partial v_{0z}}=t\\
\frac{\partial\tilde{x}}{\partial v_{0z}}=\frac{\partial\tilde{z}}{\partial v_{0x}}=0
$$
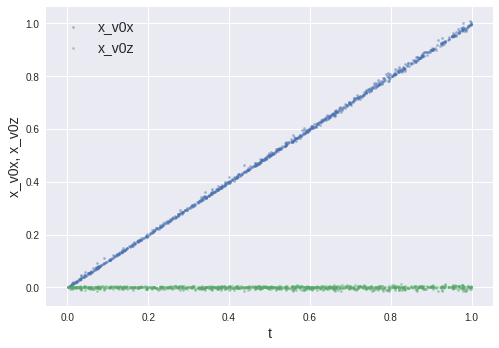
である。下図に示す結果は期待通りになっており、単に$(x, y)$を表現しているだけでなく、厳密解の特徴をよく捉えていることが分かる。
まとめ
ここまで、微分方程式で斜方投射の問題を解いてきた。あらゆる初期値に対する解が一回の計算で求まるのはかなり強力であると言える。解がよく再現できているのはもちろん、その微分等も厳密解の性質をよく再現していることが分かった。計算コストもそこまで高くないため、かなり有効な手法と言えるだろう。