はじめに
Embedding Words as Distributions with a Bayesian Skip-gram Modelという論文を読んだのでまとめていきます。
1. 対象とするトピック
1.1 キーワード
$Embedding,\ Bayes,\ Skip-gram$ 論文
1.2 先行研究
Word Representations via Gaussian Embedding
論文読み. 3 Word Representations via Gaussian Embedding (ICLR 2015)
1.3 Abstract
2. Theory
単語の埋め込みにおいて問題となるのが多義語の存在です。Skip-gramやW2G(先行研究)のように一つの単語と一つのベクトルや分布を対応させる場合は、埋め込み先の空間で多義語を適切に表現出来ないという問題が生じます。この問題への取り組みとして「単語 ー 空間での表現」の対応を「1-1」から「1-多」に変更するという方法があります。この対応関係は単語の意味が離散的に存在するという仮定に基づいています。
しかしこの論文では単語の意味が離散的に存在すると仮定しません。むしろ、一つの意味が連続的に（徐々に）変化していると考えています。そして、単語の意味が文脈に依存すると仮定します。そこで今回は文脈を事前分布として扱い、その事前分布に応じた単語の分布をベイズ的な枠組みで表現し空間に埋め込むことを試みます。
なお、以降では提案手法であるBayesian Skip-gramをBSG、と呼称します。同様に、Skip-gramをSGと呼称します。
2.1 Generative model
BSGでは単語から得たlatent meaningを用いて確率の最大化を行います。
2.2 Model definition
$p_\theta(c_j| \textbf{z})$がニューラルネットワークであるため、特徴量空間全域に渡って積分を計算することが出来ません。同様に、$p_\theta(\textbf{c}| \textbf{z})$を用いて計算する事後分布$p_\theta(\textbf{z}| \textbf{c})$も扱いが難しいです。そのため、EM algorithmが適用できません。代わりにVAEを利用しています。
2.3 Bayesian Skip-gram ELBO
KL-divergenceによって文脈と単語が与えられた場合の分布と単語のみが与えられた場合の分布との距離を計算しています。
なお、文脈と単語が与えられた場合の分布を表す$q$はエンコーダーの役割を果たしています。この$q$はガウス分布として文脈$\textbf{c}$内での単語$w$の意味がどの程度不確かであるかを埋め込みます。
2.4 Reconstruction error
2.3で登場した期待値計算をSGと同様に内積を利用した場合、問題が生じます。ベクトルの内積ではノルムで正規化することで角度を一意に定めることができます。一方で、分布間の内積計算においては分布の移動と分散の増加いずれにおいても角度が変化します。そこで関数$f$の形式を変更しています。
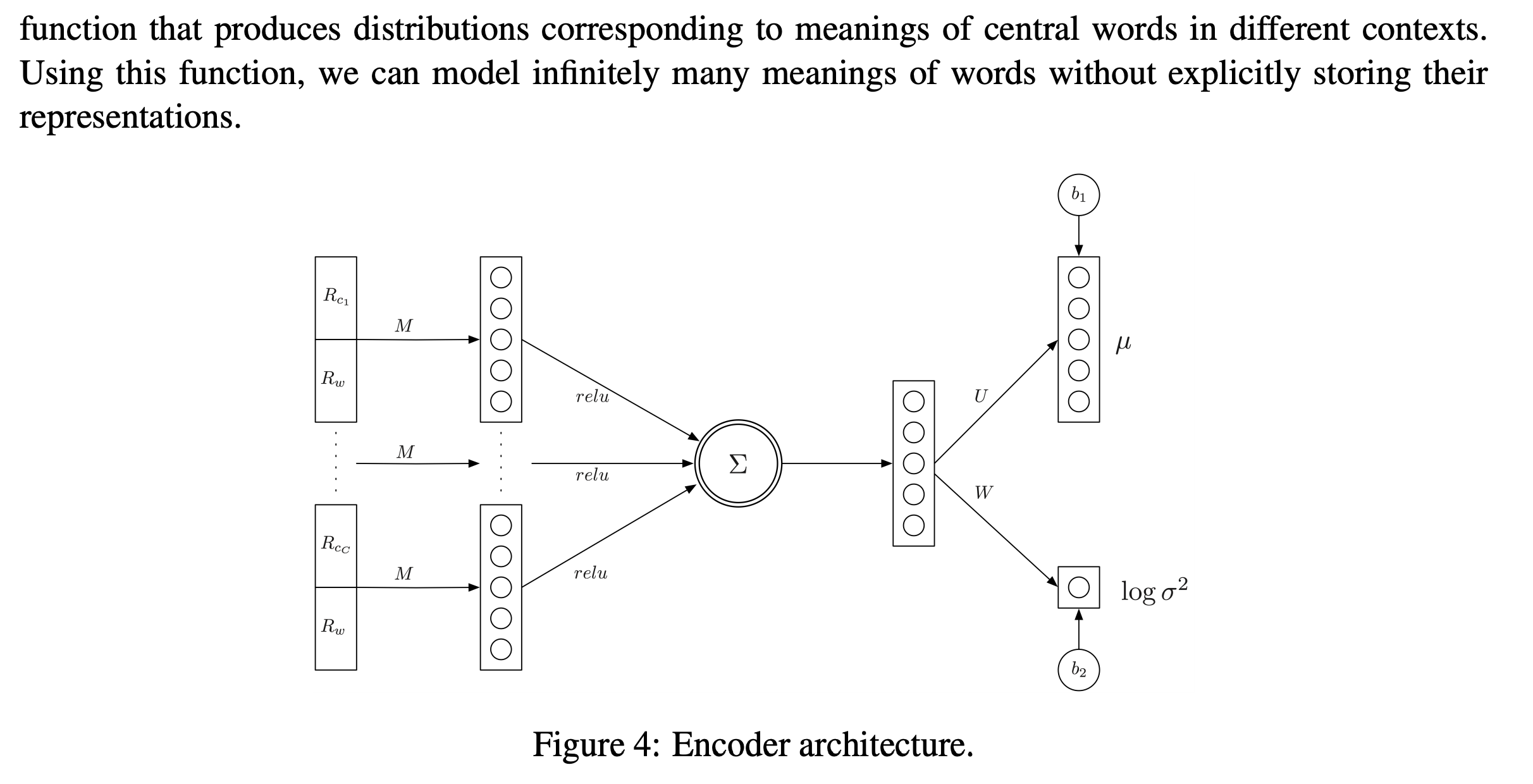
2.5 Encoder
エンコーダー$q$の構成が示されています。
2.6 Approximation of the log-partition function
-
MC法によってスケーラビリティを向上 -
negative crosse-entropyの減算をKL-divergenceの減算に変更 -
hard-margin形式へと変更
を行なった上で目的関数を得ます。
3. Experiments
3.1 Entailment recognition
二つの単語についての含意関係の判定を行います。それぞれを埋め込んだ分布から得られるKL-divergenceと分布の平均でのcosine similarityと閾値を比較して判定を行なっています。
結果は$table.3$に示されています。
3.2 Entailment directionality prediction
片方の単語がもう一方の単語を含意していることが前提とします。その上で、どちらが含意する側なのかという方向性を予測する実験を行いました。結果は$table.4$に示されています。
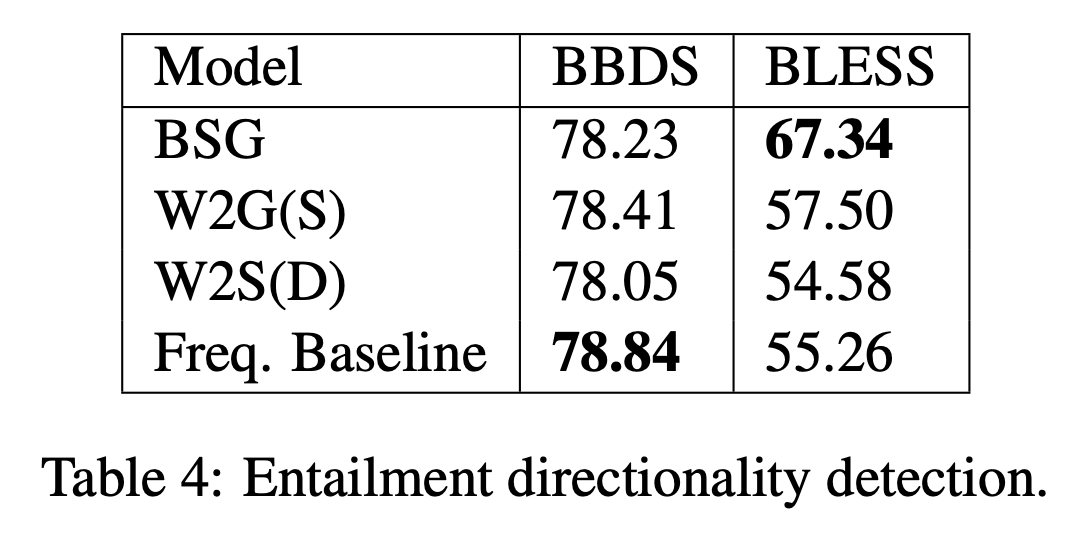$table.4$からデータセットによって結果が大きく異なることが分かります。データセットの分布によって`W2G`やベースラインの手法はパフォーマンスが大きく変動しています。そこで、`W2G`の学習している情報について考察します。
`W2G`では分散共分散行列が単語の頻出度を捉えているのではないかと考えられます。それを調べた結果が$fig.6$です。
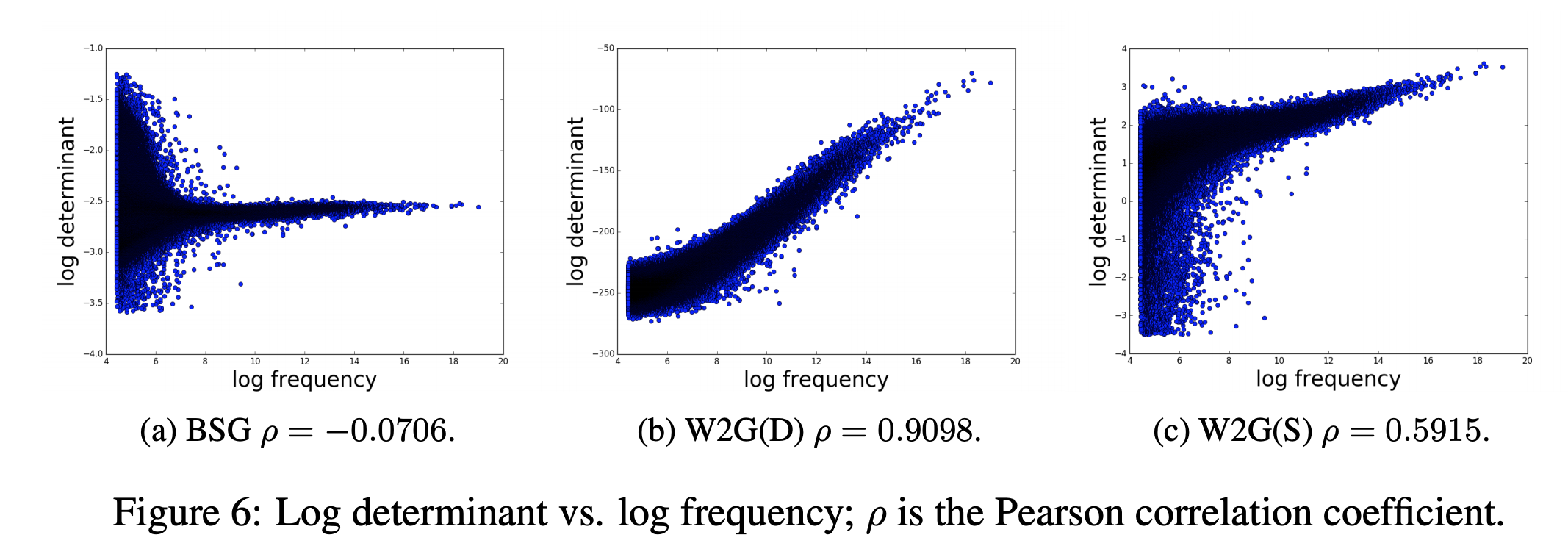$fig.6$から、`W2G`では頻出する単語ほど分散共分散行列の行列式の値が増加していることが分かります。そして、`W2G`は頻出する単語を多義語と判定する傾向があります。一方で`BSG`の分散共分散行列にはそのような傾向がないです。従って`BLESS`でのパフォーマンスの良さと合わせると、`BSG`の分散共分散行列の方がデータセットの分布に依存せずに、単語の一般性に対する正しい情報を得ていると推測されます。
References
- Arthur Bražinskas, Serhii Havrylov, Ivan Titov (2018). Embedding Words as Distributions with a Bayesian Skip-gram Model, https://arxiv.org/abs/1711.11027