はじめに
回帰モデルの性能評価メトリックと言えば、MRSE(Root Mean Squared Error),R-Square,MAE(Mean Absolute Error)が代表的です。実際には、MRSEの一択のような状況で、私自身もMRSEとたまにR-Sruareを使う程度で、MAEはほぼ言葉を知っている程度の状況でした。
こうした状況のなか、友人から「MRSEとMAEって何が違うんだろう」と聞かれたとき、気の利いた答えができませんでした。そこで、少し調べてみたところ、面白いことが見えてきたので、この場を借りて報告したいと思います。
文献リサーチ結果
とりあえず、ネットでMRSEとMAEの相違に着目した資料を検索しました。思いのほか、まとまったものがなかったのですが、最終的に以下がみつかりました。
この資料のうち私は次の記述に興味を惹かれました。
RMSE が最小となるのは、二乗誤差が最小となる時。すなわち、RMSE の最小化は最小二乗法と同値です。最小二乗法は、誤差の分布に正規分布を仮定した場合の最尤推定と一致します。
•RMSE の最小化 = 二乗誤差の最小化 = 誤差に正規分布を仮定した場合の最尤推定
MAE が最小となるのは、絶対誤差が最小となる時。絶対誤差の最小化は、誤差の分布にラプラス分布を仮定した場合の最尤推定と一致します。
•MAE の最小化 = 絶対誤差の最小化 = 誤差にラプラス分布を仮定した場合の最尤推定
一般にラプラス分布は正規分布よりも裾野が広く、多くの外れ値が観測されます。
多くの外れ値が存在するデータの誤差を評価したい、あるいは外れ値にあまり影響されない評価を行いたい場合、RMSE より MAE のほうが優れた指標であるといえるでしょう。
まとめると、
1)RMSEをコスト関数として最小化によって得られる回帰モデルのパラメータと正規分布を仮定した最尤推定によるパラメータは一致する。
2)MAEをコスト関数として最小化によって得られる回帰モデルのパラメータとラプラス分布を仮定した最尤推定によるパラメータは一致する。
3)ラプラス分布と正規分布の裾野の関係でMAEのほうが外れ値に影響されにくい。
となります。
このうち、1)は疑問はありません。pythonのscikitlearnに実装されている回帰モデルで推定されたパラメータとstatsmodelsに実装される最尤推定による回帰モデルのパラメータは、概ね一致することは経験済みです。問題は2)です。MAEをコスト関数にしても機械学習の最適化アルゴリズムは成立するのでパラメータが推計できることは理解できますが、ラプラス分布仮定の最尤推定がピンときません。さらにいうと、MAEと関連させたラプラス分布の説明は、私自身の不勉強もあってみたことがありません。そのため、MAEが外れ値の影響を受けにくいと言われてもすぐに納得するには至りません。そこで、この辺りについて少し深く調べたいと思います。
ラプラス分布とは何か
ラプラス分布はpythonでスクラッチで実装すると以下の関数で表されます。
def laplace(x,MEAN,STD):
pdf = np.exp(-np.abs(x-MEAN)/STD)/(2*STD)
return pdf
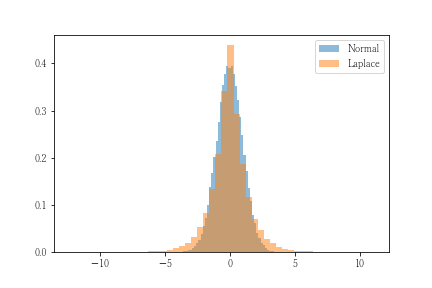
分布の形状を決定するパラメータは、平均と分散です。その意味では正規分布と同じ系統といえそうです。実際の分布を乱数を生成して確認します。乱数はscpy.stats.laplaceに含まれる関数を用いて平均=0、標準偏差=1として生成します。比較のため、同様のパラメータを設定した正規分布を重ねて表示します。
このグラフから、ふたつのことを読み取ることができます。ひとつめは、平均値という最も出現確率が高いケースにおいてラプラス分布のほうが正規分布より確率が大きいことです。これは最尤推定において影響します。つまり、平均値周辺に分布するデータがあった場合、正規分布よりもラプラス分布のほうが尤度が大きくなります。ふたつめは、裾野が大きいということです。これは、正規分布の場合、めったにないと判断されるようなデータに対してラプラス分布はそれなりにあり得ると評価されることを意味します。(今回のケースでいうと、-2~+2の外側は約5%程度の出現確率なのですが、ラプラス分布はもう少し大きい確率になることがグラフから読み取ることができます。)
つまり、こうした形状の相違が外れ値の影響を受けにくくしていると思われます。
最尤推定による平均値の推定
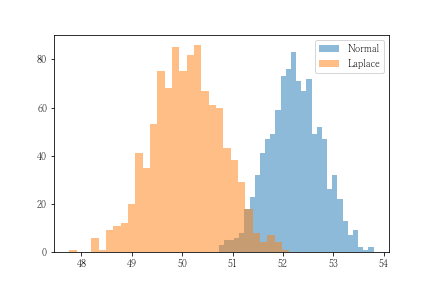
上記は形状から推論される仮説に過ぎません。そこで、トイデータを使って実験します。実験データは、平均=50、標準偏差=3、の正規分布から30個の乱数を生成して非外れ値とします。これに120という外れ値を加えて推計対象データとします。推計は、正規分布仮定の最尤推定とラプラス分布仮定の最尤推定を1000回実施してその分布の比較を行います。
グラフより正規分布仮定の最尤推定は、外れ値の影響を受けて真値よりも大きく推測されていることがわかります。一方、ラプラス分布は外れ値の影響を受けずに真値である50に近似しています。
最尤推定による回帰モデルのパラメータ推定
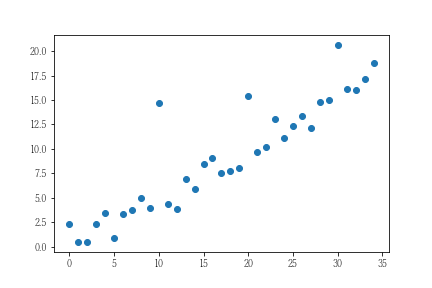
次の実験は外れ値を含むデータに対する回帰モデルのパラメータ推計を正規分布仮定とラプラス分布仮定で行います。実験用のデータは全部で33件とし、うち3件を外れ値としました。残りの30件はY=0.5Xとし、その結果に正規分布を誤差として加えています。具体的には以下の通りです。
最尤推定はstatsmodels.fomula.GLMで実装できるのですが、ラプラス分布仮定が見当たりませんでした。そこで、最尤推定の数値計算解であるstanによるサンプリングを用いて推計することにします。
stanのコードは以下の通りです。
data {
int N; // Number of Data
real X[N]; // Independent Variables
real Y[N]; // dependent Variables
}
parameters {
real a1; // normal-dist para
real a2; // laplace-dist para
real<lower=0> sigma1; // normal-dist sigma
real<lower=0> sigma2; // laplace-dist sigma
}
model {
for (n in 1:N) {
Y[n] ~ normal(a1*X[n], sigma1);
Y[n] ~ double_exponential(a2*X[n], sigma2);
}
}
簡単にstanのコードの解説をします。data部は入力データを定義した部分です。stanは入力データを配列として取り込むため、データ件数をあらかじめ定義し、変数に取り込んでいます。
prameters部は推計対象の変数を定義しています。a1およびa2がモデルの係数部分にあたります。今回は切片がないモデルとしています。sigmaは誤差の分布を表す偏差にあたります。
model部は実際に推計したいモデルを表現したものです。モデルは、平均をa1×X、a2×Xとし、各々は標準偏差sigma1、sigma2という確率分布に従うものとしています。なお、stanにおいてラプラス分布はdouble_exponentialという関数を用います。
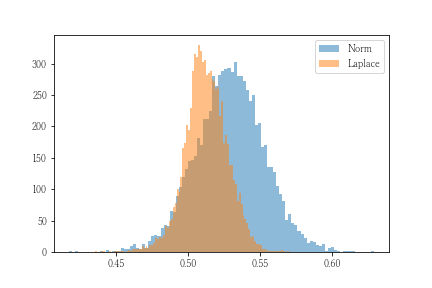
結果は、a1=0.53、a2=0.51となり、正規分布仮定のほうが外れ値に引きずられたものになりました。stanは、このパラメータそのもののサンプリング結果も取得できるので分布を可視化します。
平均値のケースよりもはっきりしませんが、相違があることがわかります。特に正規分布仮定のa1の分布は外れ値の影響を受けて分散が激しくなっていることがわかります。
外れ値とは何か
ここまで外れ値とはどういうものなのかについて議論することなく実験してきました。そこで、ここで外れ値とはどういうものなのかについて考察します。
外れ値とはその名の通り、本来の分布から見て外れた値のことです。確率分布からいうと、出現する可能性が極めて低い値といってもいいかもしれません。正規分布でいうと、『平均値-2×標準偏差~平均値+2×標準偏差』に全体の約95%のデータがカバーされます。したがって、閾値を5%とするのであれば、この範囲外の値は外れ値に相当します。
正規分布仮定において、この外れ値が混入したとしても必ずしも影響するとは限りません。非外れ値との割合によって影響の程度は異なります。先の平均値の推計のケースを対象に非外れ値と外れ値の件数の割合が推計値のどのように影響するかを可視化してみます。
このように非外れ値:外れ値が50:1あたりから影響はかなり小さくなり、200~300件ごろにはほぼないと言えそうです。外れ値をめったに出現しないものとするのであれば、この200~300件に1件というものはその通りの状況です。つまり、外れ値がその名の通りにレアな存在である限り、ラプラス分布仮定のような外れ値の影響に強いモデルとしなくても問題ないと言えそうです。
実務で回帰モデルを構築する際、取り扱うデータは数十万~数百万かと思われます。そのうち外れ値が数十件程度とすると、この外れ値の影響を考慮するほどではないでしょう。反対にそれなりの件数があるのであれば、説明変数を追加するなどという対策を取るので、外れ値の影響はかなり薄まるのではないでしょうか。
機械学習による回帰モデルのパラメータ推計
最後にRMSEとMAEをコスト関数として用いたパラメータ推計を行います。sklearnの線形回帰モデルにはコスト関数にMAEを適用するオプション設定がみあたらなかったので、tensoflowで実装して実験します。なお、データは先の最尤推定で使用したものとします。
コードは以下の通りです。
import tensorflow as tf
X1 = tf.placeholder(tf.float32,[None,1])
Y1 = tf.placeholder(tf.float32,[None,1])
w1 = tf.Variable(tf.zeros([1,1]))
P = tf.matmul(X1,w1)
# cost = tf.sqrt(tf.reduce_mean((P-Y1)**2))
cost = tf.reduce_mean(tf.abs(P-Y1))
train_step = tf.train.AdamOptimizer().minimize(cost)
sess = tf.Session()
sess.run(tf.global_variables_initializer())
cost_rate = []
for i in range(1000) :
train = sess.run(train_step,feed_dict={X1:X.reshape(-1,1),
Y1:Y.reshape(-1,1)})
tmp = sess.run(cost,feed_dict={X1:X.reshape(-1,1),
Y1:Y.reshape(-1,1)})
cost_rate.append(tmp)
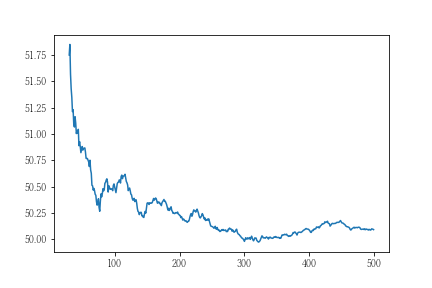
結果はRMSEは0.534、MAEは0.501ということでMAEのほうが外れ値の影響を受けないことがわかります。
まとめ
MAEをコスト関数とした機械学習の結果は、ラプラス分布仮定の最尤推定の結果と一致します。このラプラス分布はその形状の特性上、外れ値の影響を受けにくく、それゆえにMAEをコスト関数とした機械学習も外れ値の影響を受けにくいことになります。
ただし、外れ値が推計結果に影響するケースは、非外れ値と外れ値の件数比が見過ごすことができない程度のケースであって、真にレアとできるケースは必ずしも考慮する必要はありません。もう少し具体的にいうと、分析対象のデータ件数が数十件~数千件のように外れ値の影響はあるものの、モデルの改良をするほどではないような場合はMAEの活用を考えたほうがいいように思えます。