Video Deblurringとは?
Video deblurringとは動画を対象にしてフレーム内のblur(ボケやブレ)を補正する技術のことです.
図1の上段のブレているフレームを下段のよりシャープなフレームに補正することができます.

図1.Deblurringの例 (元論文より引用)
今回はCVPRというComputer Visionのトップカンファレンスに2017年に発表された次の論文を参考に、Deep Learningでこの補正を高精度に行うモデルをKerasを用いて実装してみました.
論文のポイント
この論文で高精度を達成できた要素として大きく二つ要因があると思ったのでそれぞれ簡単にまとめます.
独自データの生成
ブレありの画像とシャープな画像をペアで取得することは一見難しく思えますが、本論文ではそれを次の手法で鮮やかに解決しています.
- 240fpsの高フレームレートで動画を撮影
- 8枚に一つをサンプルすることで30fpsのシャープな動画を作成
- 8枚に一つをサンプルし、そのフレームを中心として7フレームの平均画像を取得することでブレた画像を作成
筆者は71個の動画に対してこの手法を適用し、8,000枚程度のデータセットを独自作成していました.
またこれらの画像に対して反転、拡大、回転、切り出しなどのAugmentationを行い200万枚程度に水増しして学習していました.
このように人工的に作り出したデータセットは実際のブレと性質が異なるかもしれないということも懸念されますが、結果としてこのデータセットで学習されたモデルは一般的なブレに対しても精度が高かったようです.
Skip-Connectionを含んだEncoder-Decoderモデル
本論文ではSkip-Connectionを用いたEncoder-Decoderモデルを利用しています.
Skip-Connectionを用いることで深い構造を実現可能にしています.
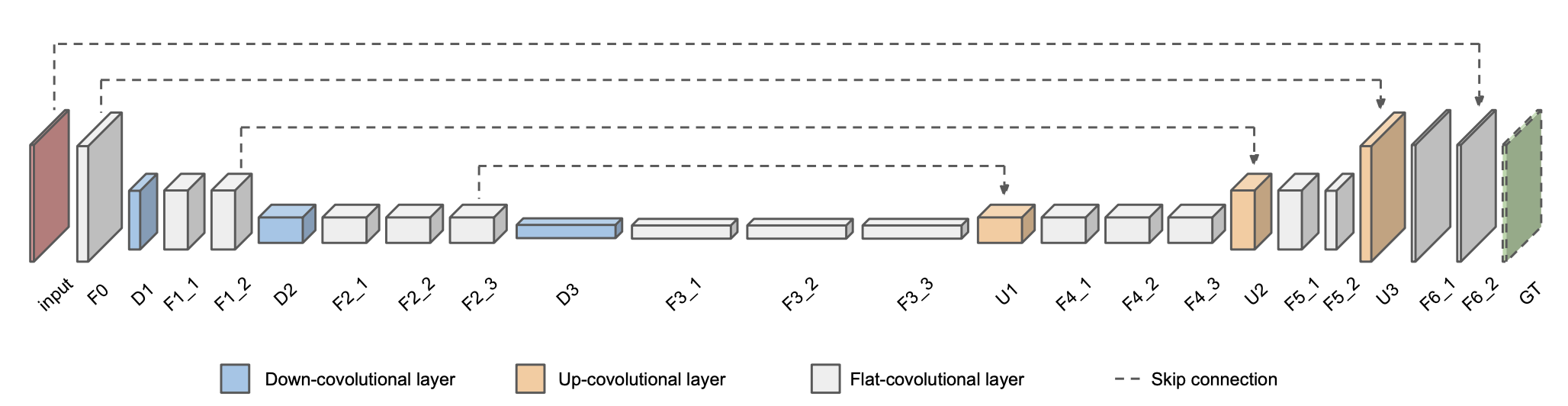
図2. モデルのアーキテクチャ (元論文より引用)
ブレが入った動画の連続する5フレームを入力(論文ではClipと呼んでいる)とし、中央のフレームのシャープな画像を出力する構造になっています.
実装
詳細は今回の実装のコード(Github)を確認してください.
本記事ではポイントとなる部分を中心に説明します.
独自データの生成
先ほど述べた周辺フレームを平均してブレありのフレームを生成する部分の実装です.
対象フレームを中心としたフレームのListを受け取り、中央のフレームをブレなしの正解画像、平均したフレームをブレありの入力画像として出力しています.
def blur_image_generator(frame_list):
surround_num = len(frame_list)
gt_img = frame_list[surround_num//2]
frame_array = np.array(frame_list)
input_img = np.mean(frame_array, axis=0).astype(np.uint8)
return gt_img, input_img
上の実装を自分で撮影した動画に当てはめてみたのがこちらになります.
平均を取るというシンプルな方法でブレが出せていることが確認できます.

図3. ブレ生成手法の適用. 左がシャープな画像で右が平均画像
元論文ではさらにOptical Flowを用いたフレームの内挿を行い、フレーム間隔の時間的な解像度を高くすることでより滑らかなブレを生成していたらしいです.
(こちらはコードや手法の詳細が論文に載っておらず断念)
Encoder-Decoderモデルの実装
Kerasで今回のモデルを実装したコードになります.
入力はClip内のフレーム数×チャンネル数(RGBの3つ)になっていることが確認できます。
このモデルに対し、80,000程度のiterationの学習を行います.
学習済みの重みもGitHubからアクセスできます.
class ModelGenerator():
def model(self, n_stack=5, input_size=128, epsilon=0.001):
# _ shows output after activation layer
inputs = Input(shape=(input_size, input_size, 3*n_stack)) # (height, width, channel*stack)
f0_1 = Conv2D(15, kernel_size=5, padding='same')(inputs)
f0_1 = BatchNormalization(epsilon=epsilon)(f0_1)
f0_1_ = Activation('relu')(f0_1) # ReLU(f0)
f0_2 = Conv2D(64, kernel_size=3, padding='same')(f0_1_)
f0_2 = BatchNormalization(epsilon=epsilon)(f0_2)
f0_2_ = Activation('relu')(f0_2)
d1 = Conv2D(64, kernel_size=3, strides=2, padding='same')(f0_2_)
d1 = BatchNormalization(epsilon=epsilon)(d1)
d1_ = Activation('relu')(d1)
f1_1 = Conv2D(128, kernel_size=3, padding='same')(d1_)
f1_1 = BatchNormalization(epsilon=epsilon)(f1_1)
f1_1_ = Activation('relu')(f1_1)
f1_2 = Conv2D(128, kernel_size=3, padding='same')(f1_1_)
f1_2 = BatchNormalization(epsilon=epsilon)(f1_2)
f1_2_ = Activation('relu')(f1_2)
d2 = Conv2D(256, kernel_size=3, strides=2, padding='same')(f1_2_)
d2 = BatchNormalization(epsilon=epsilon)(d2)
d2_ = Activation('relu')(d2)
f2_1 = Conv2D(256, kernel_size=3, padding='same')(d2_)
f2_1 = BatchNormalization(epsilon=epsilon)(f2_1)
f2_1_ = Activation('relu')(f2_1)
f2_2 = Conv2D(256, kernel_size=3, padding='same')(f2_1_)
f2_2 = BatchNormalization(epsilon=epsilon)(f2_2)
f2_2_ = Activation('relu')(f2_2)
f2_3 = Conv2D(256, kernel_size=3, padding='same')(f2_2_)
f2_3 = BatchNormalization(epsilon=epsilon)(f2_3)
f2_3_ = Activation('relu')(f2_3)
d3 = Conv2D(512, kernel_size=3, strides=2, padding='same')(f2_3_)
d3 = BatchNormalization(epsilon=epsilon)(d3)
d3_ = Activation('relu')(d3)
f3_1 = Conv2D(512, kernel_size=3, padding='same')(d3_)
f3_1 = BatchNormalization(epsilon=epsilon)(f3_1)
f3_1_ = Activation('relu')(f3_1)
f3_2 = Conv2D(512, kernel_size=3, padding='same')(f3_1_)
f3_2 = BatchNormalization(epsilon=epsilon)(f3_2)
f3_2_ = Activation('relu')(f3_2)
f3_3 = Conv2D(512, kernel_size=3, padding='same')(f3_2_)
f3_3 = BatchNormalization(epsilon=epsilon)(f3_3)
f3_3_ = Activation('relu')(f3_3)
u1 = Conv2DTranspose(256, kernel_size=4, strides=2, padding='same')(f3_3_)
u1 = BatchNormalization(epsilon=epsilon)(u1)
s1 = Average()([u1, f2_3]) # Original paper might have intended Sum layer
s1_ = Activation('relu')(s1)
f4_1 = Conv2D(256, kernel_size=3, padding='same')(s1_)
f4_1 = BatchNormalization(epsilon=epsilon)(f4_1)
f4_1_ = Activation('relu')(f4_1)
f4_2 = Conv2D(256, kernel_size=3, padding='same')(f4_1_)
f4_2 = BatchNormalization(epsilon=epsilon)(f4_2)
f4_2_ = Activation('relu')(f4_2)
f4_3 = Conv2D(256, kernel_size=3, padding='same')(f4_2_)
f4_3 = BatchNormalization(epsilon=epsilon)(f4_3)
f4_3_ = Activation('relu')(f4_3)
u2 = Conv2DTranspose(128, kernel_size=4, strides=2, padding='same')(f4_3_)
u2 = BatchNormalization(epsilon=epsilon)(u2)
s2 = Average()([u2, f1_2])
s2_ = Activation('relu')(s2)
f5_1 = Conv2D(128, kernel_size=3, padding='same')(s2_)
f5_1 = BatchNormalization(epsilon=epsilon)(f5_1)
f5_1_ = Activation('relu')(f5_1)
f5_2 = Conv2D(64, kernel_size=3, padding='same')(f5_1_)
f5_2 = BatchNormalization(epsilon=epsilon)(f5_2)
f5_2_ = Activation('relu')(f5_2)
u3 = Conv2DTranspose(64, kernel_size=4, strides=2, padding='same')(f5_2_)
u3 = BatchNormalization(epsilon=epsilon)(u3)
s3 = Average()([u3, f0_2])
s3_ = Activation('relu')(s3)
f6_1 = Conv2D(15, kernel_size=3, padding='same')(s3_)
f6_1 = BatchNormalization(epsilon=epsilon)(f6_1)
f6_1_ = Activation('relu')(f6_1)
f6_2 = Conv2D(3, kernel_size=3, padding='same')(f6_1_)
f6_2 = BatchNormalization(epsilon=epsilon)(f6_2)
f6_2_ = Activation('relu')(f6_2)
inputs_mid = self.crop(3,n_stack//2*3,(n_stack//2+1)*3)(inputs)
s4 = Average()([inputs_mid, f6_2])
s4_ = Activation('sigmoid')(s4)
model = Model(inputs=inputs, outputs=s4_)
return model
Skip-connecitonは活性化関数を通す前に次の層に伝え、結合してから活性化関数に通すような構造になっていました.
結合の方法についてはFeature fusionなどを用いることでさらに精度が上がるのかなと思いました.
結果
このようなタスクは
- 数値的にどれだけ改善しているかという定量的な評価
- 人間にとって最もらしいかという定性的な評価
の両方を行うのが普通らしいので、両方行いました.
定量的評価
元論文では次のような定量的な評価を行なっていました.
PSNRという画質の評価尺度を用いています.
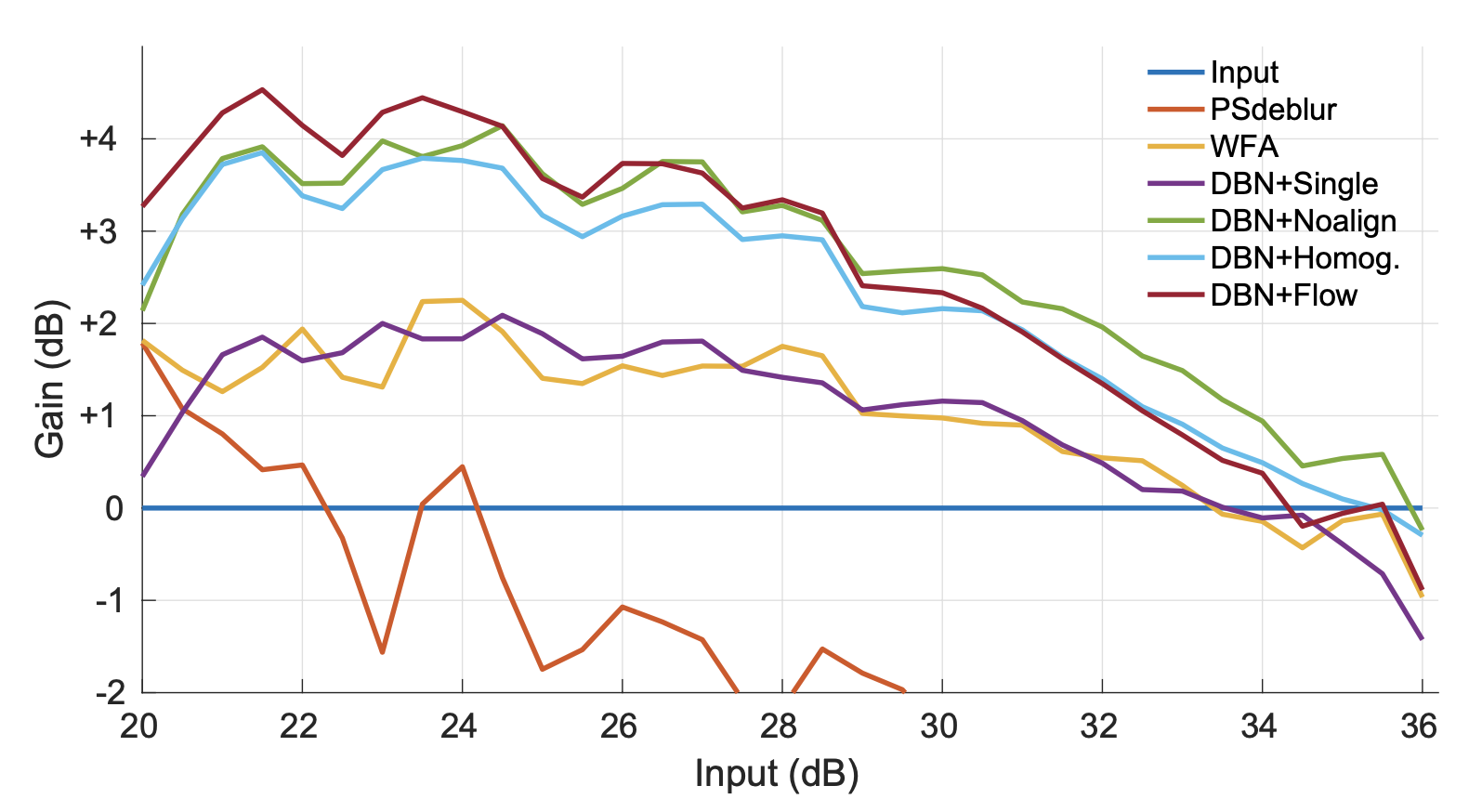
図4. モデルの性能評価. (元論文より引用)
x軸に入力に使うブレた画像の画質、y軸は出力と入力画像の画質の差をとったもので、+になるほど画質が改善していることを表しています.
DBNと書いてあるのが今回用いたモデルです.
特に画質が悪い画像を入力としたときに大きく改善する傾向があることがわかります.
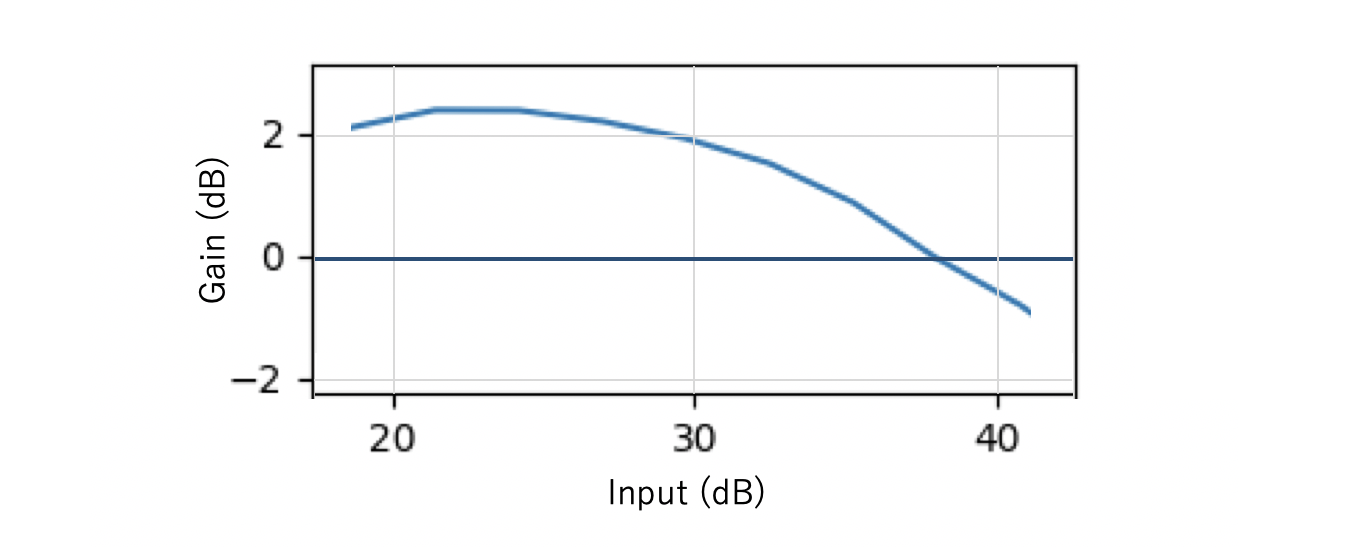
次に今回学習させたモデルの出力結果を同じように示します(図5).
最大値は2を少し超えるくらいで論文の実装には及んでいません.
理由として、
- モデルの学習の詳細がPublicになっておらず違う可能性があること
- Lossを徐々に減らしていく工夫が著者実装の方がされていたこと
などが考えられます.
それに対して入力画像の画質が高い領域(35dBあたり)に着目すると、今回実装したモデルの方が精度がいいことがわかります.
この評価に用いたデータなどについて論文に詳しく載っていなかったため、その違いもあると感じました(グラフの形状も結構違うし、、)
個人的な面白かった発見として論文の意図が見えたことがあります.
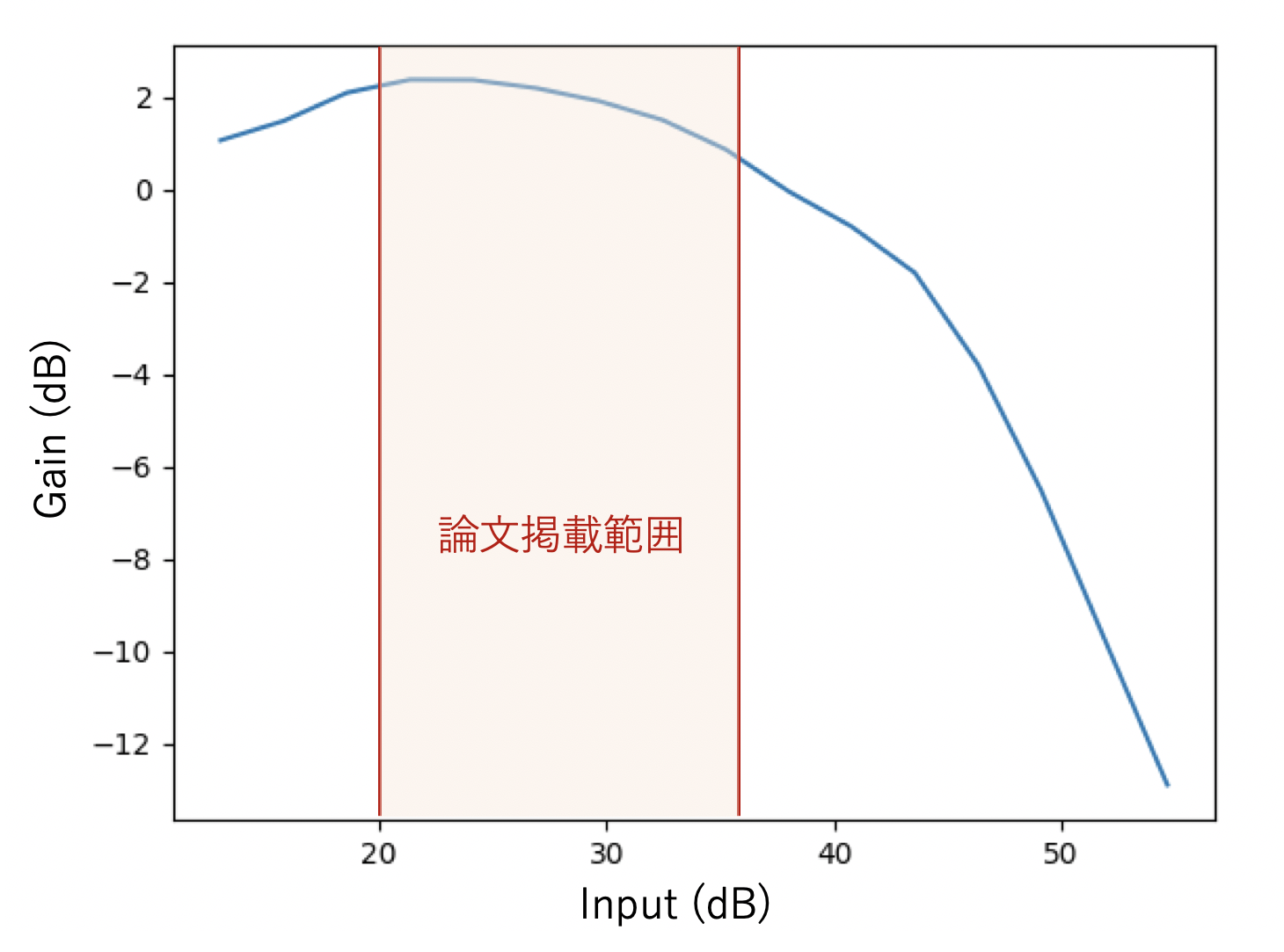
図4・図5では実際はこちらのような出力が出ていたはずなのですが、論文では赤い範囲だけを切り出して掲載しているようです.
実際はブレが少ない画像を入力すると悪化する領域がかなり広く広がっていて、現実の問題では予めground truthの高画質の画像は得られないことから、実装上この領域がどこかを見極めるのはかなり難しいと思います.
論文の主張を支えるという意図でこのように一部だけが掲載されるのは悪いことではないと思うのですが、次のfuture workに繋がりうるこういった部分が論文を読んだだけでは見つけられなくなってしまっているのはもったいないなとも感じました.
定性的評価
定性的な評価として、現実のブレ(上で述べた人工的でない自然なブレ)が入った画像を入力として、そのブレが改善しているかどうかの評価を行いました.
図4を見ると、くっきり改善しているとまではいかないが、特にブレが激しい部分において改善が見られることがわかります.

図6. ブレ補正の結果. 上段が入力画像、下段が出力.
まとめ
CVPRのような情報系のトップカンファレンスの論文を実装したのは今回が初めてでしたが、細かい評価方法やモデルの詳細など実際に実装してみないとわからないこともあるなと思いました.
物理学者のファインマンは黒板に次の言葉を残して亡くなったそうです.
「作ることができなければ、理解していないということだ」
少し大げさですがまた興味がある論文があったら実装にチャレンジしてみたいと思います.