0,前提知識
本記事ではPythonではじめるベイズ機械学習入門(以下[1])の第2章までの知識を前提としています。第3章の回帰モデルをNumpyroで実行したい方向けになっています。ですので理論等は割愛していきます。
使用ライブラリは以下、環境としてはColaboを想定している。
import pandas as pd
import numpy as np
from scipy import stats
import seaborn as sns
import matplotlib.pyplot as plt
import jax
import jax.numpy as jnp
import numpyro
import arviz as az
1,線形回帰モデル
1,サンプルデータ
true_w1 = 1.5
true_w2 = 0.8
N = 4
x_data = np.random.uniform(-5,5,size=N)
y_data = true_w1 * x_data + true_w2 + np.random.normal(0.,1.,size=N)
[1]ではプロットまでしているが割愛した。
2,構築
#モデルの定義
def model(x, y):
w1 = numpyro.sample("w1", numpyro.distributions.Normal(0, 1)) # weight
w2 = numpyro.sample("w2", numpyro.distributions.Normal(0, 1)) # bias
sigma = numpyro.sample("sigma", numpyro.distributions.HalfNormal(scale=1.0)) # observation noise
y_hat = w1 * x + w2 # linear regression relationship
with numpyro.plate("data", len(x)):
numpyro.sample("obs", numpyro.distributions.Normal(y_hat, sigma), obs=y) # observation model
#NUTSを指定
kernel = numpyro.infer.NUTS(model)
#MCMCによる推論
mcmc = numpyro.infer.MCMC(kernel,num_warmup=500,num_samples=2000,num_chains=2)
3,実行
mcmc.run(jax.random.PRNGKey(1),x=x_data, y=y_data)
以上で事後分布が得られたので、サンプルを可視化していく。
mcmc.print_summary()
以下のように表形式で出力してくれる。見づらいがまとまってるので良し。
| mean | std | median | 5.0% | 95.0% | n_eff | r_hat | |
|---|---|---|---|---|---|---|---|
| b | 1.25 | 0.36 | 1.30 | 0.70 | 1.84 | 2049.80 | 1.00 |
| sigma | 0.69 | 0.38 | 0.59 | 0.21 | 1.23 | 1221.64 | 1.00 |
| w | 1.61 | 0.09 | 1.62 | 1.48 | 1.75 | 2177.36 | 1.00 |
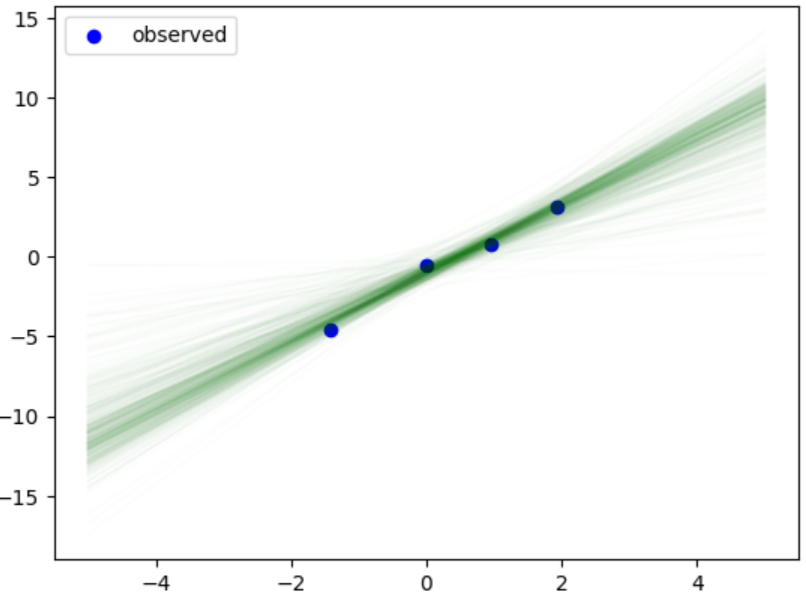
予測分布のサンプル
samples = mcmc.get_samples()
w1_samples = samples['w1']
w2_samples = samples['w2']
x_new = np.linspace(-5,5,100)
for i in range(0,4000,10):
y_pred = w1_samples[i] * x_plot_data + w2_samples[i]
plt.plot(x_new,y_pred,alpha=0.01,color="g")
plt.scatter(x_data, y_data, color='blue', label='observed')
plt.legend()
plt.show()
2,重回帰モデル
1,サンプルデータ
from mpl_toolkits.mplot3d import Axes3D
#次元
dim = 2
#データ数
N = 100
#真のパラメータ
true_w = np.array([-1.5,0.8,1.2]).reshape([3,1])
#サンプルデータ
x_data = np.random.uniform(-5,5,[N,dim])
#バイアスの次元
bias = np.ones(N).reshape([N,1])
x_data_add_bias = np.concatenate([x_data,bias],axis=1)
y_data = np.dot(x_data_add_bias,true_w) + np.random.normal(0.0,1.0,size=[N,1])
fig = plt.figure()
ax = fig.add_subplot(111,projection="3d")
ax.scatter(x_data[:,0],x_data[:,1],y_data)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("Y")
plt.show()
2,構築
def model(x, y):
sigma = numpyro.sample("sigma", numpyro.distributions.HalfNormal(1.0)) # observation noise
with numpyro.plate("para", x.shape[1]):
w = numpyro.sample("w", numpyro.distributions.Normal(0,1).expand([x.shape[1]])) # weight
y_hat = jnp.dot(w,x.T)
with numpyro.plate("data", x.shape[0]):
numpyro.sample("obs", numpyro.distributions.Normal(y_hat, sigma), obs=y.ravel()) # observation model
#NUTSを指定
kernel = numpyro.infer.NUTS(model)
mcmc = numpyro.infer.MCMC(kernel,num_warmup=500,num_samples=2000,num_chains=2)
3,実行
mcmc.run(jax.random.PRNGKey(0),x=x_data_add_bias,y=y_data)
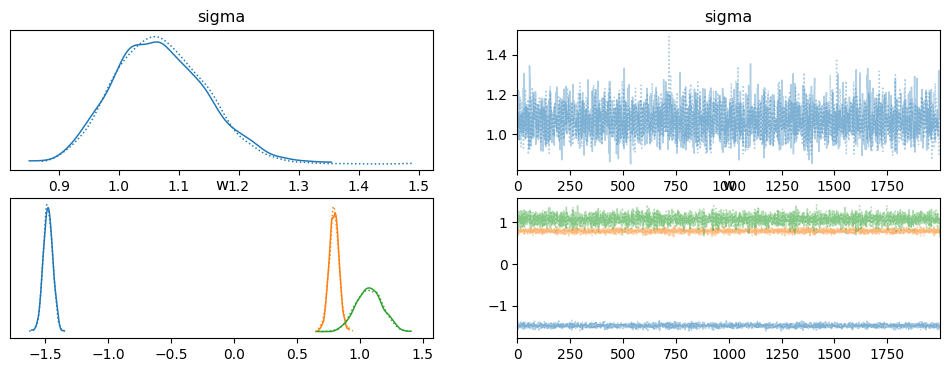
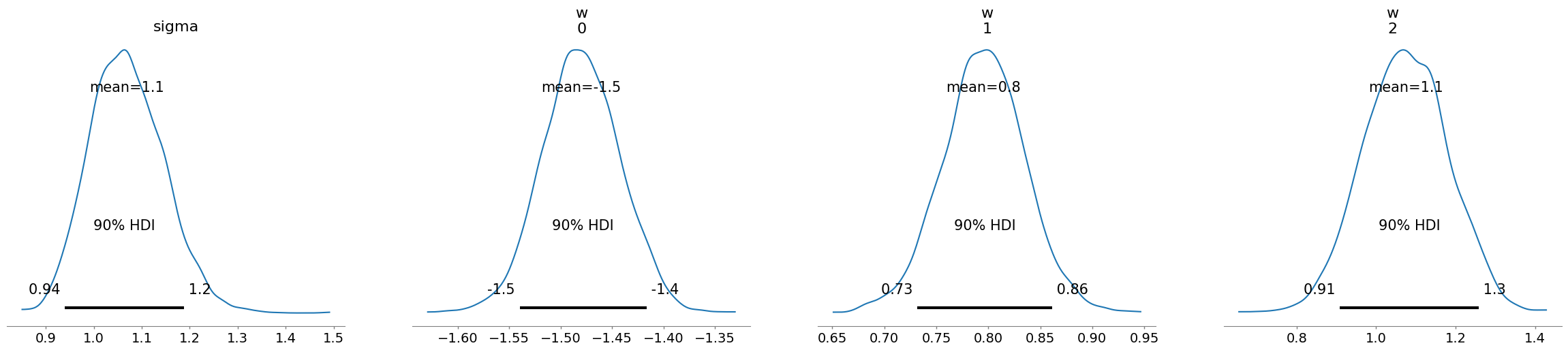
結果を可視化すると
az.plot_trace(mcmc)
az.plot_posterior(mcmc,hdi_prob=0.9)