はじめに
分布を予測するガウス過程回帰(GPR : Gaussian Process Regression)を用いて、Boston Housing Dataset の住宅価格予測を行ってみる。参考文献を以下に示す。
- GPR : Gaussian Process Regression について
- ガウス過程回帰(Gaussian Process Regression, GPR)~予測値だけでなく予測値のばらつきも計算できる!~
- Gaussian Process
- Boston Housing Dataset について
- Boston Housing:ボストンの住宅価格(部屋数や犯罪率などの13項目)の表形式データセット
データセットの準備
scikit-learn のデータセットを用いる。人種差別問題に関わる B の項目については除外して分析を行う。GPRでは目的変数の標準化が必須のようなので、それをStandardScalerを用いて行う。その後、データセットを訓練データ、テストデータに分ける。
# 必要なモジュールのインポート
import numpy as np
import pandas as pd
import sklearn
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# データセットの読み込み
boston = load_boston()
X_org = boston.data
y = boston.target.reshape(-1, 1)
# 'B'の項目の削除
X = np.delete(X_org, 11, 1)
# 目的変数の標準化
scaler_y = StandardScaler().fit(y)
y_ss = scaler_y.transform(y)
# データセットの分割(train:test = 9.0:1.0)
X_train, X_test, y_train_ss, y_test_ss = train_test_split(X, y_ss, test_size=0.1, random_state=0)
GPR のモデル作成、学習
平均と標準偏差を予測するモデルを作成。学習(fit)する。カーネル関数は良く使われる、「ConstantKernel() * RBF() + WhiteKernel()」を使用した。カーネル関数の比較については別記事で行いたいと思う。
# 必要なモジュールのインポート
from sklearn.gaussian_process import GaussianProcessRegressor
from sklearn.gaussian_process.kernels import ConstantKernel, RBF, WhiteKernel
# カーネル関数の設定
kernel = ConstantKernel() * RBF() + WhiteKernel()
# モデルの作成
gpr = GaussianProcessRegressor(kernel=kernel, alpha=0, random_state=0)
# モデルの学習
gpr.fit(X_train, y_train_ss)
GaussianProcessRegressor(alpha=0,
kernel=1**2 * RBF(length_scale=1) + WhiteKernel(noise_level=1),
random_state=0)
学習結果のカーネル関数のパラメータを確認する。
# kernel関数のパラメータの確認
print(gpr.kernel_)
213**2 * RBF(length_scale=447) + WhiteKernel(noise_level=0.0976)
学習済みモデルを用いてテストデータの予測
作成したモデルを用いて予測(predict)を行う。
# 学習済みモデルを用いて予測を行う
pred_mu_ss, pred_sigma_ss = gpr.predict(X_test, return_std=True)
# 標準化を戻す
y_test = scaler_y.inverse_transform(y_test_ss)
pred_mu = scaler_y.inverse_transform(pred_mu_ss)
pred_sigma = pred_sigma_ss.reshape(-1, 1) * scaler_y.scale_
# リストにまとめる
result = list(zip(y_test.reshape(-1), pred_mu.reshape(-1), pred_sigma.reshape(-1)))
# データフレームへ
df_result = pd.DataFrame(result, columns=['obs', 'pred_mu', 'pred_sigma'])
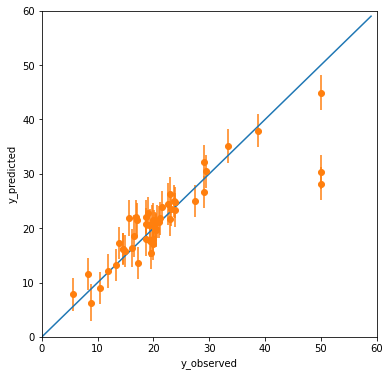
予測結果からエラーバー(1σ)も込みで Observed-Predicted Plot (yyplot) を作成してみる。
# 必要なモジュールのインポート
import matplotlib.pyplot as plt
def make_yyplot(df_result, filename, xy_min = 0, xy_max = 60):
# 直線の準備
x = np.arange(xy_min, xy_max)
y = x
# Observed-Predicted Plot(yyplot) の作成
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111)
ax.plot(x, y)
ax.errorbar(df_result['obs'], df_result['pred_mu'], yerr = df_result['pred_sigma'], fmt='o')
ax.set_xlim(xy_min, xy_max)
ax.set_ylim(xy_min, xy_max)
ax.set_xlabel('y_observed')
ax.set_ylabel('y_predicted')
plt.savefig(filename, bbox_inches="tight") # png で保存する場合
plt.close()
make_yyplot(df_result, 'GPR_boston_yyplot.png')
NGBoost の時(Boston データセットで NGBoost を試す)と同様、概ね予測は正しくできてそうだが、(y_observed, y_predicted) = (50, 28) 付近の2点に外れ値がある。
負の対数尤度 NLL:Negative Log Likelihood による比較
NGBoost の元論文ではいろんな手法を負の対数尤度の平均値を使って比較していた。もちろん GPR を用いて Boston データセットでの値も論文に載っているので、この分析結果も論文の値が再現できているか比較してみる。
Boston のデータセットに対してGPRの論文の結果では、「$2.37 \pm 0.24$」とあった。
# NLL を計算する関数を定義
def calc_NLL(x, mu, sigma):
term_1 = 1 / 2 * np.log(2 * np.pi * sigma ** 2)
term_2 = ((x - mu) ** 2) / (2 * sigma ** 2)
mns_l = term_1 + term_2
mean = round(mns_l.mean(), 2)
std = round(mns_l.std(), 2)
print(mean, '+/-', std)
return None
# NLL を出力
calc_NLL(df_result['obs'], df_result['pred_mu'], df_result['pred_sigma'])
3.24 +/- 4.49
NLLの平均値もNLLの標準偏差も論文よりだいぶ大きな値となってしまった。これは前述した二つの外れ値による影響が大きいと思われる。
説明変数の標準化
目的変数については標準化したが、説明変数は標準化していない。サンプルコードによっては標準化しているものもあったので、参考までに検証してみる。
# 説明変数の標準化
scaler_X = StandardScaler().fit(X)
X_ss = scaler_X.transform(X)
# データセットの分割(train:test = 9.0:1.0)
X_train_ss, X_test_ss, y_train_ss, y_test_ss = train_test_split(X_ss, y_ss, test_size=0.1, random_state=0)
# モデルの作成
gpr2 = GaussianProcessRegressor(kernel=kernel, alpha=0, random_state=0)
# モデルの学習
gpr2.fit(X_train_ss, y_train_ss)
GaussianProcessRegressor(alpha=0,
kernel=1**2 * RBF(length_scale=1) + WhiteKernel(noise_level=1),
random_state=0)
# kernel関数のパラメータの確認
print(gpr2.kernel_)
1.48**2 * RBF(length_scale=3.35) + WhiteKernel(noise_level=0.0611)
# 学習済みモデルを用いて予測を行う
pred_mu_ss2, pred_sigma_ss2 = gpr2.predict(X_test_ss, return_std=True)
# 標準化を戻す
pred_mu2 = scaler_y.inverse_transform(pred_mu_ss2)
pred_sigma2 = pred_sigma_ss2.reshape(-1, 1) * scaler_y.scale_
# リストにまとめる
result2 = list(zip(y_test.reshape(-1), pred_mu2.reshape(-1), pred_sigma2.reshape(-1)))
# データフレームへ
df_result2 = pd.DataFrame(result2, columns=['obs', 'pred_mu', 'pred_sigma'])
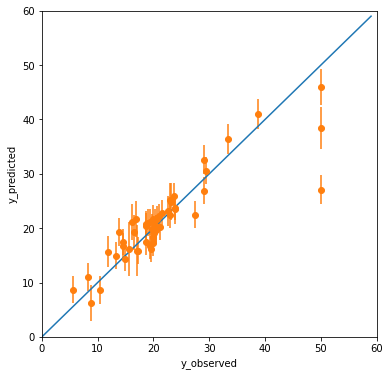
make_yyplot(df_result2, 'GPR_boston_yyplot2.png')
# NLL を出力
calc_NLL(df_result2['obs'], df_result2['pred_mu'], df_result2['pred_sigma'])
3.13 +/- 5.28
NLL の平均値は少しだけ改善されたが、その分標準偏差が大きくなってしまった。
RMSE, R2 の値
モデルの当てはまりの良さも確認しておきたいので、RMSE、R2の値も計算しておく。
# 必要なモジュールのインポート
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score
# RMSE の出力
print('RMSE:', np.sqrt(mean_squared_error(df_result['obs'], df_result['pred_mu'])))
# R2 の出力
print('R2:', r2_score(df_result['obs'], df_result['pred_mu']))
RMSE: 4.767112929953258
R2: 0.7358254691417548
説明変数を標準化した場合の値は
# RMSE の出力
print('RMSE:', np.sqrt(mean_squared_error(df_result2['obs'], df_result2['pred_mu'])))
# R2 の出力
print('R2:', r2_score(df_result2['obs'], df_result2['pred_mu']))
RMSE: 4.3180096352226
R2: 0.7832559028849013
となる。説明変数を標準化した方が、少しだけ当てはまりが良くなる。
NGBoost の結果と比較すると、すこしだけ GPR の方が精度が良いように見える。
おわりに
NGBoost と同様、あまり意味のない考察だが、二つの外れ値が無かった場合 NLL の値がどうなっていたかを検証してみる。index 番号が 1, 37 のデータが外れ値であったので、
# 外れ値だけ取り除いた結果のデータフレーム
_df_result = df_result.drop(index=[1, 37]).copy()
# NLL を出力
calc_NLL(_df_result['obs'], _df_result['pred_mu'], _df_result['pred_sigma'])
2.36 +/- 0.43
となる。だいぶ論文の値と近くなった。
NGBoost と同様に、データセットの選び方によっても結果が有る程度変わると思われるので、本当に精度を調べようとしたら交差検証などが必要かもしれない。また、実装のサンプルはあってもNLLの部分についてのコードは公開されていないので、計算方法が若干違うかもしれない…。
標準化の前処理だけで GPR を実装することができた。カーネル関数の組み合わせや選び方は多岐にわたるので、次の記事では代表的ないくつかのカーネル関数について、検討を行ってみたいと思う。