Boston データセットで NGBoost を試す

はじめに

ブースティングアルゴリズムで分布を予測する NGBoost を用いて、Boston Housing Dataset の住宅価格予測を行ってみる。参考文献を以下に示す。

• NGBoost: Natural Gradient Boosting for Probabilistic Prediction について
• User Guide
• git hub : https://github.com/stanfordmlgroup/ngboost
• 元論文の arXiv : https://arxiv.org/abs/1910.03225
• Boston Housing Dataset について
• Boston Housing：ボストンの住宅価格（部屋数や犯罪率などの13項目）の表形式データセット

NGBoost の導入方法などは git hub に載っている。とは言っても、pip か conda でインストールすればいいだけである。

データセットの準備

scikit-learn のデータセットを用いる。人種差別問題に関わる B の項目については除外して分析を行う。データセットをデータフレームに入れて準備したら、訓練データ、検証データ、テストデータに分ける。

データセットの準備

# 必要なモジュールのインポート
import numpy as np
import pandas as pd
import sklearn
from sklearn.datasets import load_boston
from sklearn.model_selection import train_test_split

# データセットの読み込み、データフレーム化
boston = load_boston()
df = pd.DataFrame(boston.data, columns=boston.feature_names)
df['PRICE'] = boston.target

# 'B'の項目の削除 
df.drop('B', axis=1, inplace=True)

# データセットの分割(train:val:test = 7.2:1.8:1.0)
df_tmp, df_test = train_test_split(df, test_size=0.1, random_state=0)
df_train, df_val = train_test_split(df_tmp, test_size=0.2, random_state=0)

X_train = df_train.iloc[:, 0:12]
y_train = df_train.iloc[:, 12]
X_val = df_val.iloc[:, 0:12]
y_val = df_val.iloc[:, 12]
X_test = df_test.iloc[:, 0:12]
y_test = df_test.iloc[:, 12]

NGBoost のモデル作成、学習

予測する分布は正規分布（平均と標準偏差を予測する）としてモデルを作成。学習（fit）する。

モデルの作成、学習

# 必要なモジュールのインポート
from ngboost import NGBRegressor
from ngboost.scores import LogScore
from ngboost.distns import Normal

# モデルの作成
model = NGBRegressor(Dist=Normal, Score=LogScore, verbose=3, random_state=0, n_estimators=2000)

# モデルの学習
_ = model.fit(X_train, y_train, X_val=X_val, Y_val=y_val, early_stopping_rounds=100)

出力

[iter 0] loss=3.6315 val_loss=3.6271 scale=1.0000 norm=6.6313
[iter 100] loss=2.7131 val_loss=2.7905 scale=2.0000 norm=4.9550
[iter 200] loss=2.1577 val_loss=2.5025 scale=2.0000 norm=3.3565
[iter 300] loss=1.8707 val_loss=2.7237 scale=2.0000 norm=2.8833
== Early stopping achieved.
== Best iteration / VAL211 (val_loss=2.4994)

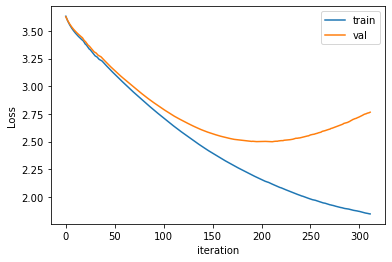
学習時の Loss をプロットしてみると、以下の様になる。

Lossの可視化

# 必要なモジュールのインポート
import matplotlib.pyplot as plt

# 可視化
fig = plt.figure()
ax = fig.add_subplot(111)

ax.plot(model.evals_result['train']['LOGSCORE'], label="train")
ax.plot(model.evals_result['val']['LOGSCORE'], label='val')

ax.set_xlabel('iteration')
ax.set_ylabel('Loss')
ax.legend()

#plt.savefig('NGBoost_boston_loss.png', bbox_inches="tight") # png で保存する場合
#plt.close()
plt.show()

early stopping の出力結果の通り 211 付近で検証データの loss が最小になっているのが分かる。

学習済みモデルを用いてテストデータの予測

作成したモデルを用いて予測（pred_dist）を行う。

予測

# 学習済みモデルを用いて best の loss 値の所で予測を行う
y_pred=model.pred_dist(X_test, max_iter=model.best_val_loss_itr)

# 予測結果から、平均(μ)と標準偏差(σ)を取り出す
y_mu=y_pred.params['loc']
y_sigma=y_pred.params['scale']

# 実測値とまとめてデータフレームへ
df_result = pd.DataFrame(list(zip(y_test, y_mu, y_sigma)), columns=['obs', 'pred_mu', 'pred_sigma'], index=y_test.index)

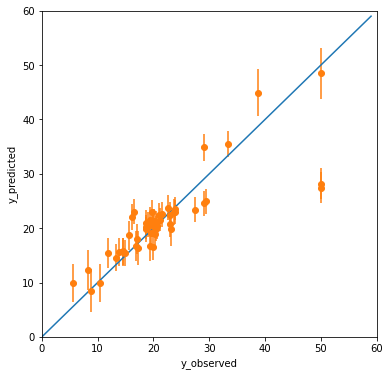
エラーバー(1σ)も込みで Observed-Predicted Plot (yyplot) を作成してみる。

yyplotの可視化

# グラフの最小値、最大値
xy_min = 0
xy_max = 60

# 直線の準備
x = np.arange(xy_min, xy_max)
y = x

# Observed-Predicted Plot(yyplot) の作成
fig = plt.figure(figsize=(6, 6))
ax = fig.add_subplot(111)

ax.plot(x, y)
ax.errorbar(df_result['obs'], df_result['pred_mu'], yerr = df_result['pred_sigma'], fmt='o')

ax.set_xlim(xy_min, xy_max)
ax.set_ylim(xy_min, xy_max)

ax.set_xlabel('y_observed')
ax.set_ylabel('y_predicted')

#plt.savefig('NGBoost_boston_yyplot.png', bbox_inches="tight") # png で保存する場合
#plt.close()
plt.show()

概ね予測は正しくできてそうだが、(y_observed, y_predicted) = (50, 28) 付近の2点が外れ値である。

負の対数尤度 NLL:Negative Log Likelihood による比較

NGBoost の元論文ではいろんな手法を負の対数尤度の平均値を使って比較していた。ある1サンプルのデータ($x$)と得られた正規分布($\cal{N}(\mu, \sigma)$)の離れ度合いは負の対数尤度で表される。小さければ小さい方がモデルの精度が良いことを表す。

-l \left( \mu , \sigma ; x \right) = \frac{1}{2} \ln \left( 2 \pi \sigma^2 \right) + \frac{1}{2\sigma^2} \left(x - \mu \right)^2

Boston のデータセットに対して論文の結果では、「$2.43 \pm 0.15$」とあるので、今回の検証ではどの程度の値になったのか確認してみる。

NLLの計算

# NLL を計算する関数を定義
def calc_NLL(x, mu, sigma):
    term_1 = 1 / 2 * np.log(2 * np.pi * sigma ** 2)
    term_2 = ((x - mu) ** 2) / (2 * sigma ** 2)
    mns_l = term_1 + term_2
    
    mean = round(mns_l.mean(), 2)
    std = round(mns_l.std(), 2)
    
    print(mean, '+/-', std)
    
    return None

# NLL を出力
calc_NLL(df_result['obs'], df_result['pred_mu'], df_result['pred_sigma'])

出力

3.57 +/- 5.88

NLLの平均値もNLLの標準偏差も論文よりだいぶ大きな値となってしまった。これは前述した二つの外れ値による影響が大きいと思われる。

RMSE, R2 の値

モデルの当てはまりの良さも確認しておきたいので、RMSE、R2の値も計算しておく。

RMSE,R2の計算

# 必要なモジュールのインポート
from sklearn.metrics import mean_squared_error
from sklearn.metrics import r2_score

# RMSE の出力
print('RMSE:', np.sqrt(mean_squared_error(df_result['obs'], df_result['pred_mu'])))

# R2 の出力
print('R2:', r2_score(df_result['obs'], df_result['pred_mu']))

出力

RMSE: 5.13956050244782
R2: 0.692933788925969

特段精度が良いわけではなかった。

おわりに

これはあまり意味のない考察だが、二つの外れ値が無かった場合 NLL の値がどうなっていたかを検証してみる。index 番号が 371, 372 のデータが外れ値であったので、

外れ値を除外した場合の検証

# 外れ値だけ取り除いた結果のデータフレーム
_df_result = df_result.drop(index=[371, 372]).copy()

# NLL を出力
calc_NLL(_df_result['obs'], _df_result['pred_mu'], _df_result['pred_sigma'])

出力

2.4 +/- 0.89

となる。だいぶ論文の値に近づいたと思われる。

データセットの選び方によっても結果が有る程度変わると思われるので、本当に精度を調べようとしたら交差検証などが必要かもしれない。また、実装のサンプルはあってもNLLの部分についてのコードは公開されていないので、計算方法が若干違うかもしれない…。

NGBoost は前処理がほとんど要らないので、とても簡単に実装することができた。今後は、別手法も試して NGBoost との比較などしていければと思う。