Go to Qiita Advent Calendar Top
LoginSignup
2
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

Day 23

FUJITSU Advent Calendar 2025

@rochiai

高精度計算（Dot2、Ozaki Scheme I）

Last updated at Posted at 2025-12-22

まえがき

以前の記事で高精度計算の準備としTowSumやTwoProductなどのエラーフリー変換を紹介しました。今回はそれらを用いた内積の高精度計算手法Dot2に加え、近年話題になっているOzaki Schemeと呼ばれる行列の高精度計算手法について紹介します。

内積の高精度計（Dot2）

内積を高精度に計算するDot21という有名な手法があります。Dot2を簡単に説明すると、和と積のエラーフリー変換（TwoSumとTwoProduct）を用いて内積を高精度に計算するアルゴリズムです。名前に2が入っているのは、現在精度の約2倍の精度で内積を計算し、その結果を現在精度に丸めるためです2。すなわち、倍精度の要素を持つベクトルでDot2を実行する場合は約四倍精度で内積を計算できるので、倍精度で普通に内積を計算するよりも高精度な結果が期待できます。

Dot2のアルゴリズムは以下です。TwoSumやTwoProductのアルゴリズムは前回の記事に載せているので省略します。

Dot2.py
def Dot2(x, y):
    assert len(x) == len(y)
    [p, s] = TwoProduct(x[0], y[0])
    for i in range(1, len(x)):
        [h, r] = TwoProduct(x[i], y[i])
        [p, q] = TwoSum(p, h)
        s = s + (q + r)
    return p + s

実験

Dot2でちゃんと高精度に計算できているか確認するために以下のような問題を設定します。ただし、$\rm{u}$は倍精度なら$2^{-53}$、単精度なら$2^{-24}$となる単位相対丸めです。

$$a = (1+2\rm{u}, 2\rm{u}), b = (1-\rm{u}, 2\rm{u})$$

上記の設定で数学的に内積計算すると結果は$1+\rm{u}+2\rm{u}^2$となります。そのため、数値計算で最近点丸めを適用する場合は上記を正の方向に丸めた$1+2\rm{u}$が真値に対して最も近い結果となります。

しかし、計算順序などを変更せずにこれを素直に数値計算すると結果は$1$となり、上記で示した真値に最も近い値に対して$2\rm{u}$の誤差が発生します。これは、以下のとおり内積時の各中間結果が現在精度に丸められてしまうためです。

$$ \rm{fl}(a \cdot b) = \rm{fl}(\color{red}{\rm{fl}(1+\rm{u}-2\rm{u}^2)} + 4\rm{u}^2) = \rm{fl}(\color{red}{1}+4\rm{u}^2) = 1 $$

実際に以下の実験でも確認できます。

test_dot.py
import numpy as np

u = 2**-53
a = [1+2*u, 2*u]
b = [1-u, 2*u]
c = np.dot(a, b)

if c == 1.0:
    print("dot(a, b)=1.0")
実行結果
dot(a, b)=1.0

Dot2では中間結果を現在精度の約2倍精度で計算するので、以下のとおり単純に現在精度で計算するよりも高精度な結果が得られます。今回の問題設定では真値に対して最も近い$1+2\rm{u}$が得られました。

test_Dot2.py
from Dot2 import Dot2

u = 2**-53
a = [1+2*u, 2*u]
b = [1-u, 2*u]

c = Dot2(a, b)

if c == 1.0+2*u:
    print("Dot2(a, b)=1.0+2u")
実行結果
Dot2(a, b)=1.0+2u

行列の高精度計算（Ozaki Scheme）

行列に対する高精度計算はDot2を繰り返し適用することで実現していました。つまり、以下のようなイメージです。この方法では内積単位で高精度計算を実行するため計算量が膨大になる（純粋な行列積の約10倍）という課題がありました。

Dot2による行列積の高精度計算イメージ
for i in range(M):
  for j in range(N):
      C[i][j] += Dot2(A[i][:], B[:][j])

それを解決する方法の1つとして提案されたのがOzaki Scheme I3です。この手法の肝は行列積を$C := AB$としたとき、行列$A$と$B$の計算で計算誤差が発生しないようにそれらを分割することです。分割数が行列積の精度に影響するため、精度を高めたければ分割数（＝メモリ使用量および計算量）を増やす必要があります。どの程度行列を分割すればよいかは行列の性質次第なので、メモリ使用量や計算量を抑えたければ問題に適した分割数を見極める必要があります。

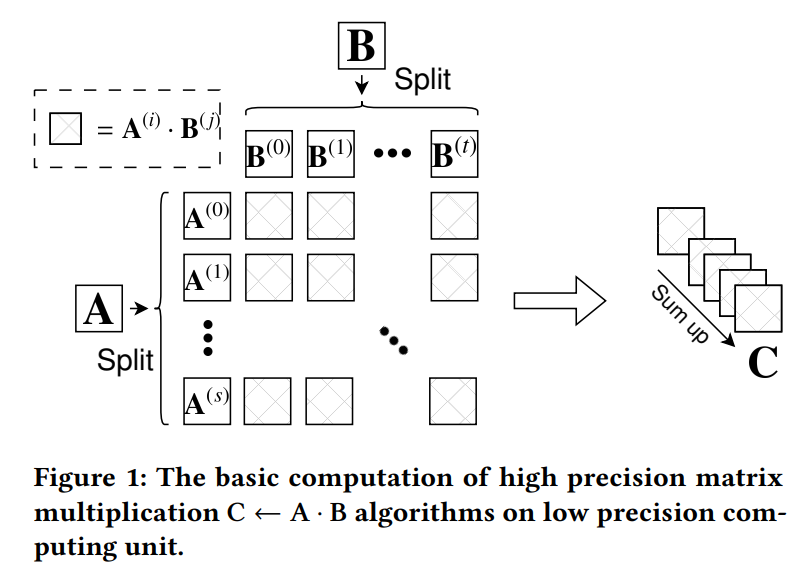
image.png
図1：Ozaki Scheme I のイメージ（引用：DGEMM on Integer Matrix Multiplication Unit4）

Dot2ではそれを構成するTwoSumやTwoProductがelementwise-place splittingのイメージで仮数部のみを考慮して処理しています。そのため、各要素に対して逐一エラーフリー変換を適用しなければならず、演算量が増大していました。

一方、Ozaki Scheme Iでは行列を分割する際にshared-place splittingのイメージで行列の行または列ベクトルの指数部を加味して分割します。すなわち、複数要素に対して誤差が出ないようにまとめて前処理しているため要素ごとの高精度計算が不要となり、BLAS等の高度にチューニングされたライブラリを用いて効率的な高精度行列積が可能となります。

image.png
図2：分割のイメージ（引用：DGEMM on Integer Matrix Multiplication Unit4）

実装の詳細な意味は論文に譲り、まずはOzaki Scheme Iの行列分割アルゴリズムを以下に示します。

Ozaki Scheme Iの行列分割アルゴリズム
def split_mat(M, max_split_num):
    [m, n] = M.shape
    beta = np.ceil((-np.log2(u)+np.log2(n))/2)
    D = []
    for s in range(max_split_num):
        mu = np.max(np.abs(M), axis=1)
        if np.max(mu) == 0:
            return D
        w = np.power(2.0, np.ceil(np.log2(mu))+beta).reshape(m, 1)
        S = np.matlib.repmat(w, 1, n)
        D.append((M+S)-S)
        M = M - D[s]
    return D

次いでOzaki Scheme Iの本体のアルゴリズムを以下に示します。
このアルゴリズム内ではNumPyのmatmul関数で行列積を実行しているとおり、この部分をBLAS等の既存のチューニング済みライブラリに置換可能なのでDot2等の既存の行列積の高精度計算手法よりも高速に演算可能となります。

Ozaki Scheme I本体のアルゴリズム
def ozaki_scheme_I(A, B, k):
    [ma, na] = A.shape
    [mb, nb] = B.shape
    assert na == mb

    D = split_mat(A, k)
    E = split_mat(np.transpose(B), k)
    ha, hb = len(D), len(E)
    for i in range(hb):
        E[i] = np.transpose(E[i])

    l = 0
    G = []
    for r in range(min(ha, k-1)):
        for s in range(min(hb, k-1)):
            if r+s < k:
                l = l + 1
                G.append(np.matmul(D[r], E[s])) # 行列積ライブラリで高速に計算可能

    F = np.zeros((mb, nb))
    for r in range(ha):
        for s in range(k-r, hb):
            F = F + E[s]
            G.append(np.matmul(D[r], F)) # 行列積ライブラリで高速に計算可能

    C = G[0]
    for i in range(1, l):
        C = C + G[i]
    return C

実験

行列の分割とOzaki Scheme Iの動作確認をします。
まず、以下のような乱数で生成した$(4, 4)$行列に対して最大分割数5を指定して行列の分割を実行した結果、行列は3分割されました。分割が増えるにつれて要素の指数が減少しているため、適切に行列分割できてそうです。

行列の分割
★分割前の行列
A=[[0.63696169 0.26978671 0.04097352 0.01652764]
 [0.81327024 0.91275558 0.60663578 0.72949656]
 [0.54362499 0.93507242 0.81585355 0.0027385 ]
 [0.85740428 0.03358558 0.72965545 0.17565562]]

★分割後の行列
 A'=[([[0.6369617 , 0.26978672, 0.04097354, 0.01652765],
       [0.81327021, 0.91275555, 0.60663575, 0.72949654],
       [0.543625  , 0.93507242, 0.81585354, 0.00273848],
       [0.85740429, 0.03358555, 0.72965544, 0.1756556 ]]),
    ([[-1.12106502e-08, -1.74363723e-09, -2.01845936e-08, -1.72119492e-08],
       [ 2.79804855e-08,  2.83237114e-08,  2.64271218e-08, 2.23449295e-08],
       [-5.67355407e-09,  1.76017956e-09,  1.79925337e-08, 2.43705873e-08],
       [-1.50422217e-08,  2.69045852e-08,  1.80790494e-09, 1.71937451e-08]]),
    ([[ 0.00000000e+00,  2.22044605e-16, -3.33066907e-16, -2.22044605e-16],
       [-6.66133815e-16,  3.33066907e-16,  6.66133815e-16, 3.33066907e-16],
       [-1.11022302e-16,  7.77156117e-16,  6.66133815e-16, 2.22044605e-16],
       [-2.22044605e-16,  2.22044605e-16, -6.66133815e-16, 4.44089210e-16]])]

行列をもう1つ用意し、Ozaki Scheme Iで行列積を実行してみます。実装があっているかの確認のため、NumPyの行列積と結果を比較しました。

Ozaki Scheme Iの実行
def main():
    seed = np.random.default_rng(0)
    A = seed.random(size=(4, 4))
    B = seed.random(size=(4, 4))

    C1 = np.matmul(A, B)
    C2 = ozaki_scheme_I(A, B, 5)

    print('C1=', C1)
    print('C2=', C2)
    print("error", np.linalg.norm(np.abs((C1-C2)/C1), np.inf))

NumPyの結果（C1）とOzaki Scheme Iの結果（C2）の相対誤差の最大値ノルムが倍精度で表せるギリギリくらいの精度なので、結果は合っていそうです。

実行結果
C1= [[0.59399706 0.4048912  0.42406815 0.49045493]
 [1.60126181 1.26105489 1.96302568 1.81321142]
 [0.99966807 0.72537169 1.60547585 1.63623546]
 [1.31048283 0.86263454 1.12804676 1.16813814]]
C2= [[0.59399706 0.4048912  0.42406815 0.49045493]
 [1.60126181 1.26105489 1.96302568 1.81321142]
 [0.99966807 0.72537169 1.60547585 1.63623546]
 [1.31048283 0.86263454 1.12804676 1.16813814]]
error 5.563613422368135e-16

さて、このOzaki Scheme Iは2012年時点で本来の意味では行列積の高精度計算手法として提案されましたが、近年では行列の分割＝低精度化ととらえてNVIDIA GPUのTensor Coreによる低精度行列積エンジンを用いた倍精度、単精度行列積のエミュレーション手法が提案されています45。これは、Tensor Coreによる低精度演算の性能は倍精度、単精度性能と比較して非常に高いため、単純に倍精度や単精度で行列積を実行するよりOzaki Scheme Iを使ったほうが高速になるケースがあるためです。現在はAIによりGPGPUの利用が当たり前になりつつあるため、とても注目される手法となりました。

＃ほんとは Ozaki Scheme IIの紹介もしたかったけど、ここまでにして次回に持ち越します。

  1. TAKESHI OGITA, SIEGFRIED M. RUMP, AND SHIN’ICHI OISHI, ACCURATE SUM AND DOT PRODUCT, published in SIAM Journal on Scientific Computing (SISC), 26(6):1955-1988, 2005 ↩

  2. DotKという現在精度の約K倍精度で内積を計算する一般化されたアルゴリズムもあり、↑の論文で提案されています。 ↩

  3. Ozaki K, Ogita T, Oishi S and Rump SM (2012) Error-free transformations of matrix multiplication by using fast routines of matrix multiplication and its applications.Numerical Algorithms 59(1): 95–118. ↩

  4. Ootomo H, Ozaki K and Yokota R (2024) Dgemm on integer matrix multiplication unit.The International Journal of High Performance Computing Applications in Press. ↩ ↩2 ↩3

  5. Y. Uchino, K. Ozaki, T. Imamura: Performance Enhancement of the Ozaki Scheme on Integer Matrix Multiplication Unit, International Journal of High Performance Computing Applications, 39:3 (2025), 462--476. ↩

2
2
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
2
2

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?