【重回帰分析】多重共線性が生じていても、偏回帰係数は真値の周りで偏りなく推定されますか?
解決したいこと
タイトルの通りです。
多重共線性の解決方法として、変数の選択を行うこと、変数を合成すること、正則化を行うことが一般的だと思います。このうち、変数の選択・変数の合成はやりたくないです(全ての説明変数の偏回帰係数をどうしても知りたいからです)。
正則化、とくにリッジ回帰がこの目的に合致すると思うのですが、リッジ回帰以外の解決方法がもしあったら、知りたくて質問させていただきました。
多重共線性について知っていること
(この点も理解が怪しいので、ツッコミよろしくお願いします。)
重回帰分析において、相関係数の絶対値が大きい説明変数のペアがあると、そのペアの偏回帰係数の推定結果が「不安定」になる現象が多重共線性だと理解しています。
「不安定」とは、ペアの相関係数がわずかに変化するだけで、偏回帰係数の推定結果が大きく変化してしまうという意味です。現実的には、データセットからデータをいくつか取り除いて(このとき、ペアの相関係数が変化するので)偏回帰係数が変化するかどうかを調べることが、多重共線性のチェック方法の一つだと認識しています。
疑問
多重共線性が生じて偏回帰係数が不安定になっていたとしても、平均的には各偏回帰係数が真値から偏りなく分布するのか知りたいです。
もし、偏りなく分布するのであれば、データセットをランダムにn分割して、重回帰モデルを分割されたデータセット各々に対して立て、偏回帰係数の推定結果の平均値を取れば、真値が得られるのではないかと思っています。
自分で試したこと
2つの説明変数を持った、重回帰モデルを用いて実験してみました。一つ目の変数はv1で真値は10、二つ目の変数はv2で真値は20のつもりです。
実験1:多重共線性なしの場合
多重共線性がないケースで相関係数を変化(0.0~0.1の区間を0.001刻み)させて、偏回帰係数の推定結果それぞれ101個を得ました。
#R
#多重共線性がないケース
set.seed(20230902)
result=data_frame()
for (r in seq(0.0,0.1,0.001)){
x=rnorm(n=1000,mean=0,sd=3)
e1=rnorm(n=1000,mean=0,sd=3)
e2=rnorm(n=1000,mean=0,sd=3)
v1=sqrt(r)*x+sqrt(1-r)*e1
v2=sqrt(r)*x+sqrt(1-r)*e2
data=data_frame(v1=v1,v2=v2)
data=data %>% mutate(y=v1*10+v2*20+rnorm(n=1000,mean=0,sd=1))
model=data %>% lm(y~v1+v2,data=.)
intercept=model$coefficients[1]
b_v1=model$coefficients[2]
b_v2=model$coefficients[3]
temp=data_frame(r=r,intercept=intercept,b_v1=b_v1,b_v2=b_v2)
result=rbind(result,temp)
}
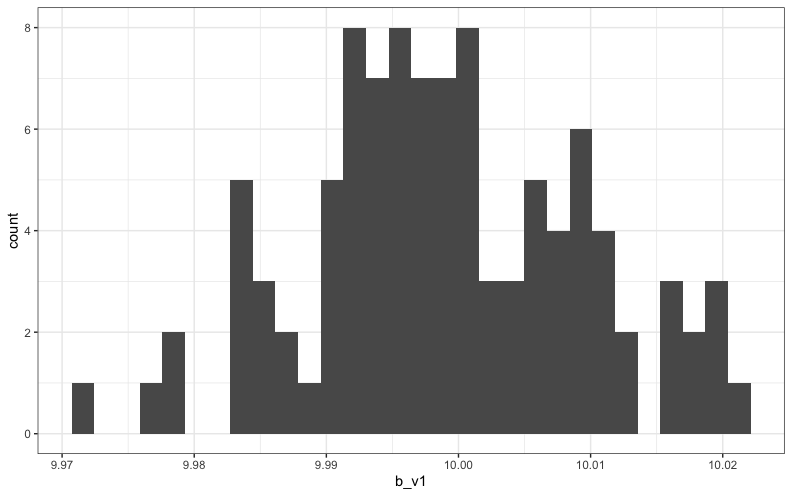
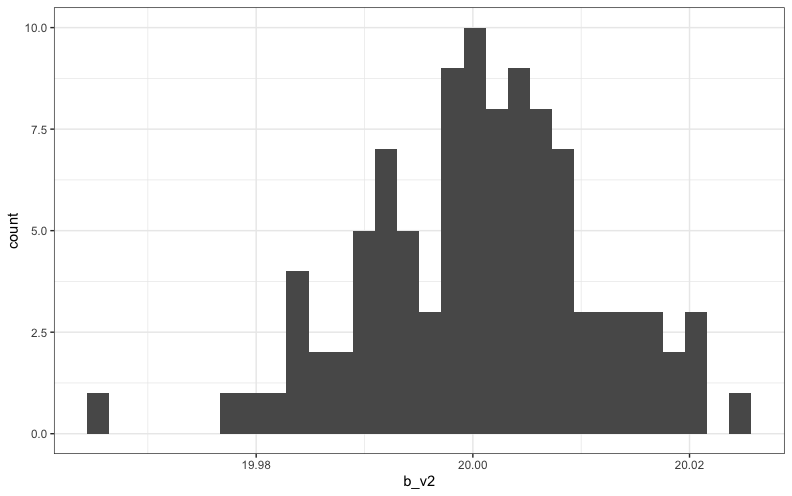
偏回帰係数のヒストグラムは次のようになりました。
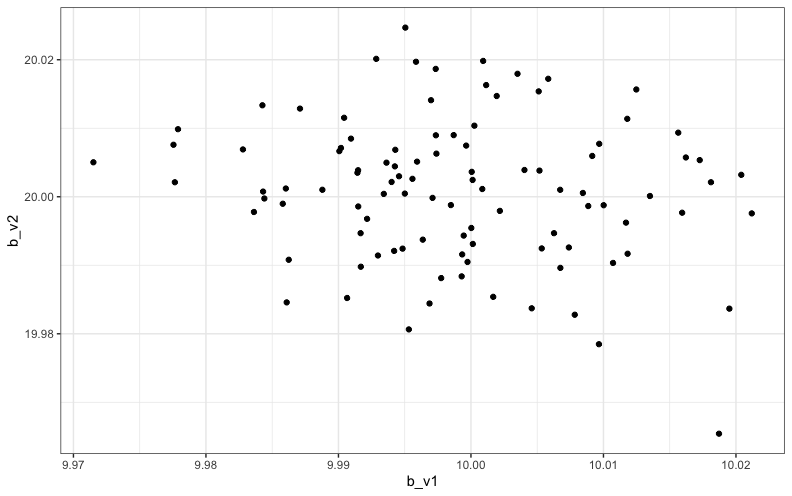
偏回帰係数の散布図は次のようになりました。
偏回帰係数の平均値と標準偏差を示します。
| v1 | v2 | |
|---|---|---|
| 平均値 | 9.99 | 20.00 |
| 標準偏差 | 0.01 | 0.01 |
実験2:多重共線性ありの場合
多重共線性があるケースで相関係数を変化(0.900~0.999の区間を0.001刻み)させて、偏回帰係数の推定結果それぞれ100個を得ました。
#R
#多重共線性があるケース
set.seed(20230902)
result_multico=data_frame()
for (r in seq(0.900,0.999,0.001)){
x=rnorm(n=1000,mean=0,sd=3)
e1=rnorm(n=1000,mean=0,sd=3)
e2=rnorm(n=1000,mean=0,sd=3)
v1=sqrt(r)*x+sqrt(1-r)*e1
v2=sqrt(r)*x+sqrt(1-r)*e2
data=data_frame(v1=v1,v2=v2)
data=data %>% mutate(y=v1*10+v2*20+rnorm(n=1000,mean=0,sd=1))
model=data %>% lm(y~v1+v2,data=.)
intercept=model$coefficients[1]
b_v1=model$coefficients[2]
b_v2=model$coefficients[3]
temp=data_frame(r=r,intercept=intercept,b_v1=b_v1,b_v2=b_v2)
result_multico=rbind(result_multico,temp)
}
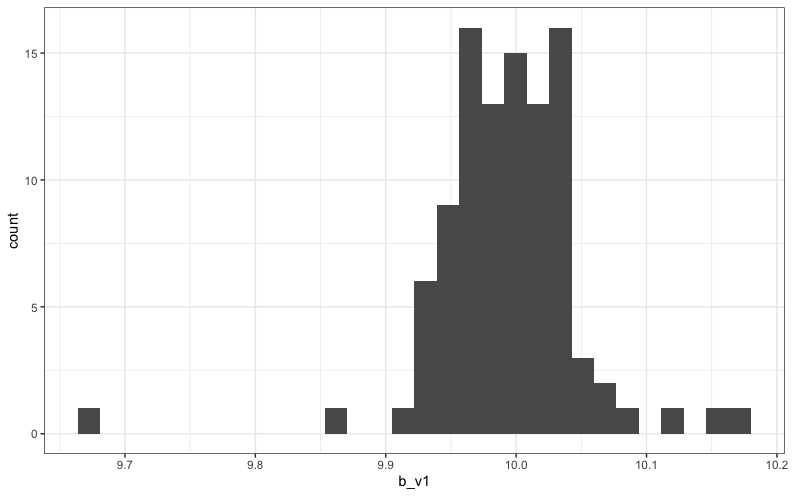
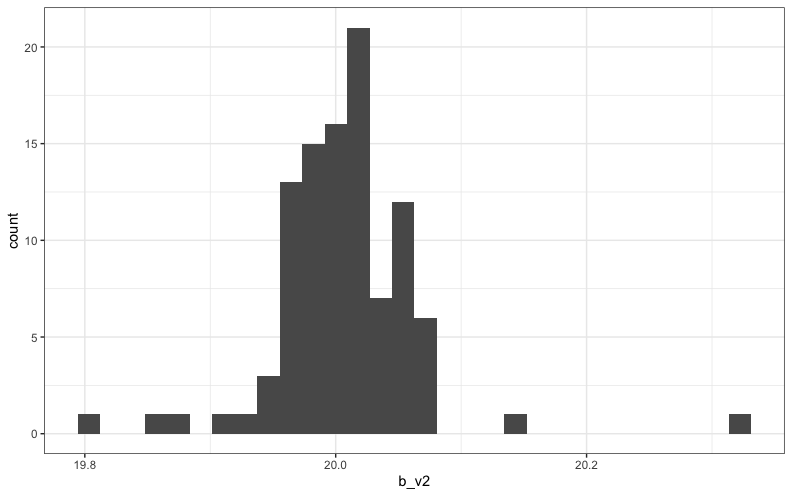
偏回帰係数のヒストグラムは次のようになりました。
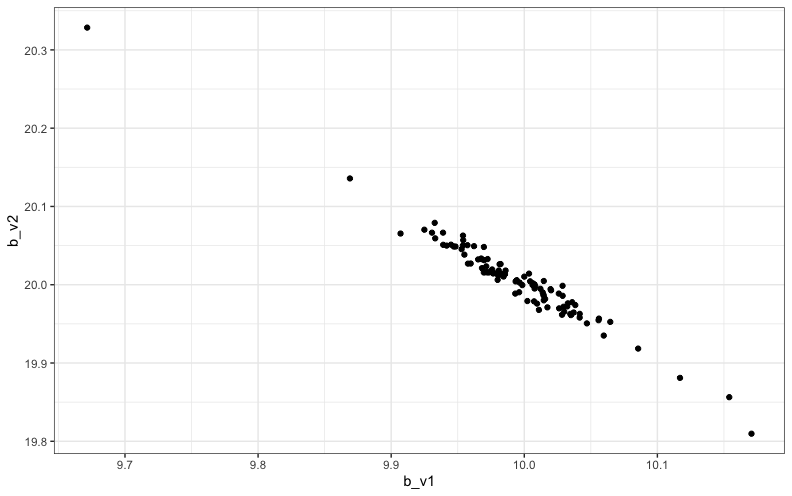
偏回帰係数の散布図は次のようになりました。負の相関がみられるのは、多重共線性をきちんと(?)発生させられている証拠だと思っています。
| v1 | v2 | |
|---|---|---|
| 平均値 | 9.99 | 20.01 |
| 標準偏差 | 0.06 | 0.06 |
最後に
このような実験をやるのは初めてなので、不備があったら、ぜひコメントで教えていただきたいです。(追試も大歓迎です!)