前回はUCB1やMCTSのアルゴリズムを簡単に解説行ってきました。今回はDefault PolicyおよびTree Policyなどについての項目についての解説をA Survey of MCTSに沿って進めていきます。
UCB1 / UCT (Upper Confidence Tree)について
UCBをベースにしたTree Searchモデルということから、上記A Survey of MCTSではUCT=(Upper Confidence Tree)のアルゴリズムの説明がされており、__Tree Policy / Default Policy / Best Child__の各々のロジックが組み込まれています。
紹介されているUCTアルゴリズムを下記の図の様に抜粋し6つのパートを色分けしてみました。
Tree Policy / Default Policy / Best Child
それでは、上記アルゴリズムを重要性が高いものから各々説明していきます。
| Policy | 説明 |
|---|---|
|
Best Child ピンクの囲み④ |
Best Childは上記ロジックの順序からすると4番目の説明となりますが、Tree Policyの中で使用される重要なロジック・パターンなので先に説明をします。ここでは親Nodeから拡張された既存の子Nodeから最も高いRewardを算出した子Nodeを選択します。 argmax以下で取得されるNodeのReward計算式 ($\frac{Q(v^{\prime})}{N(v^{\prime})}+c \sqrt{\frac{2lnN(v)}{N(v^{\prime})}} $)は、前回説明したUCBのことで、第二項に探索Biasが加算されているので探索数が多いNodeでは0に限りなく近づき第一項の平均値と同等になります。 |
|
Tree Policy ブルーの囲み② |
このPolicyはTreeから新たにNodeを派生するか(__EXPAND(v)のところです)、もしくは既存のNodeから最も高いRewardを出力できるNodeを先に説明した(Best Child)__で選択します。 下記の三目並べ(Tic Tac Toe)の例題で提示されている様に、親Nodeから子Nodeを派生できれば、Nodeを拡張できますし。もし拡張できるNodeが存在しない場合は既存のNodeから選ぶということになります。候補を選ぶ基準はUCB1で定義されたRewardが使用されます。 |
| Default Policy ブルーの囲み⑤ | Default Policyは、別名__Simulation__とも呼ばれています。このPolicyでは__最後__までNode下のLeaf(例えば囲碁などのゲームであれば、相手方もしくは自身が一つ駒を進めていくこと)を拡張していきます。Tree PolicyでNode下から終点に達するまでLeafを拡張していくか(引き分けまで駒を打ち続ける)、もしくは閾値を超えたLeafを伸ばしていきます。強化学習で使用された言葉を借りていうならば、決定した行動で状況を更新していくということです。 |
三目並べでTree PolicyおよびDefault Policyを解説
Tree Policy / Default Policyを三目ならべで簡単に解説します。図はTim Weeler氏のAlpha Go Zero How and Why it worksより抜粋してあります。
Tree Policy
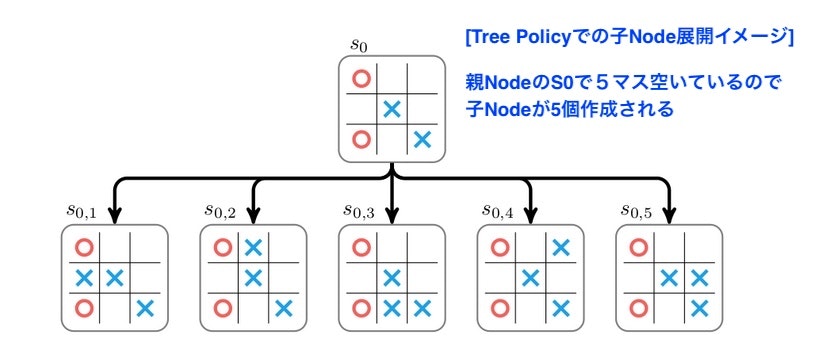
状況$S_0$では既に○2つ、✖️2つの駒が打たれています。ここで✖️は駒を打つ空いている箇所が5箇所あるので、✖️の立場で考えると、子Nodeが5個作成出来る環境になっています。Tree Policyではこの子Nodeをまず最低1個作成することから始まります。どの子Nodeを作成するかはランダムに決定します。子Nodeを1個作成した後は、子Nodeを次のロジックDefault Policyに渡します。
Default Policy
例えば、上記Tree Policyで$S_{0,1}$が選択されDefault Policyに渡された場合、✖️もしくは◯は$S_{0,1}$から空いている盤面をランダムに探してお互い駒を打ち続けます。この行動は勝敗が決まるか、もしくは引分けに到るまで行われます。この図の例では盤面上に最後まで駒が打ち続けられましたが、✖︎が勝利した結果となっています。ここで勝利がつけば、勝利者には➕のReward、敗者であれば、➖のRewardをセットして、後のUCBの計算に使用する様にします。

以上、MCTSをあまりに簡単に解説してしまいましたが、次回はPythonで実装しながら解説を行いたいと考えています。
