今回はデータ分析における流れを備忘録を兼ねて記録していきます。
モデルを作成する時間よりも、データの準備や出力結果の考察に時間や労力を使うのかなといった印象です。
GitHubにソースコードを置いております。
時間がない人向け: この記事の概要
今回はBank Marketingを用いてモデリングをしました。
今回の目的は、定期預金に申し込むかどうかを予測します。
使用したモデルは
- 決定木
- ランダムフォレスト
- LightGBM
の3つです。
結果は以下の通りです。
| Model | Accuracy | AUC | Calculation Time |
|---|---|---|---|
| Decision Tree | 0.79 | 0.59 | - |
| Random Forest | 0.86 | 0.77 | 1.20 sec |
| LightGBM | 0.86 | 0.78 | 0.09 sec |
それぞれのモデルでメリデメがあるため、自分が何をしたいのかという目的を具体化してから、モデル検討に移ることがベターです。
分類問題のモデリングでは、解釈性を優先したい場合は決定木、精度を重視したい場合はLightGBMをまず試してみるのがいいかと思われます。
LightGBMは欠損値を含んでいても学習できるメリットがあるため、素早く実装できるのも強みです。そのため、ランダムフォレストよりもLightGBMの方が初手としては優秀かなといった印象です。
本題
今回のもくじです。
- データ確認
- 今回使用するデータ
- データ分析の目的
- データ確認
- データ説明
- 欠損値確認
- 異常値確認
- データの可視化
- モデリング
- 決定木
- ランダムフォレスト
- LightGBM
- まとめ
- 付録
データ確認
今回使用するデータ
今回使用するデータはBank Marketingを使用させていただきます。
こちらのデータはURLから詳細を閲覧することができます。
データ分析の目的
今回の目的は顧客が定期預金に申し込むかどうかを予測することを目的としています。
こうした目的の確認は見落としがちですが、非常に重要なプロセスになります。また、分析方針で悩んだ際や次の手が思いつかない場合にはこうしたところに立ち返り状況を整理することも重要になります。
データの確認
bank_marketing = fetch_ucirepo(id=222)
X = bank_marketing.data.features
y = bank_marketing.data.targets
display(X, y)
display(X.dtypes, y.dtypes)
print(f"X shape: {X.shape}, y shape: {y.shape}")
X: 45,211rows, 16columns
y: 45,211rows, 1columns
自分一人しか見ないコードでも出来るだけ奇麗なコーディングを心がけると良いです。
出力の形を整えてあげることで翌日以降の自分を助けることとなります。
また、データの前処理ではX, yをjoinして一つのデータフレームとして扱います。
df = X.join(y)
こうすることで欠損値を削除する際に説明変数と目的変数のレコード数の齟齬が発生することを防ぎます。
データの説明
今回は説明変数をXという変数に代入し、目的変数をyという変数に代入しました。
| 変数名 | データ型 | 補足 |
|---|---|---|
| age | int64 | 18~95歳 |
| job | object | 11種類 |
| marital | object | 婚約状況 |
| education | object | 教育レベル |
| default | object | 不履行があるか |
| balance | int64 | 年間平均残高(ユーロ) |
| housing | object | 住宅ローンがあるか |
| loan | object | 個人ローンがあるか |
| contact | object | 連絡先の通信タイプ(携帯か電話) |
| day_of_week | int64 | 最後に連絡した日 |
| month | object | 最後に連絡した月 |
| duration | int64 | - |
| campaign | int64 | キャンペーン中に顧客に対して行われたコンタクト数 |
| pdays | int64 | 顧客が前回のキャンペーンで最後にコンタクトをとってから経過した日数 |
| previous | int64 | このキャンペーンの前に顧客のために行われたコンタクト数 |
| poutcome | object | 前回のマーケティングキャンペーン結果 |
jobの説明
jobにはそれぞれ以下のような要素が含まれています。説明欄はcahtGPTに補足してもらいました。
| Job | Description |
|---|---|
| Management(管理職) | 経営者、マネージャー、スーパーバイザーなど、企業や組織の運営に関わる職種。 |
| Technician(技術者) | 技術職に従事する人々。エンジニア、メカニック、IT技術者などが含まれます。 |
| Blue-collar(ブルーカラー労働者) | 体力労働や製造業、建設業に従事する労働者。工場労働者や配管工などが該当します。 |
| Admin.(事務職) | 事務やオフィスワークに従事する職種。データ入力、秘書業務、総務などが含まれます。 |
| Services(サービス業) | サービス提供に従事する職業。レストランの従業員、理美容師、医療関係者、警備員などが含まれます。 |
| Retired(退職者) | 定年退職した人々を指します。現在は働いていないが、過去に労働市場に参加していた人々。 |
| Self-employed(自営業者) | 自分でビジネスを運営する人々。フリーランサーや個人事業主などが含まれます。 |
| Entrepreneur(起業家) | 新しいビジネスやプロジェクトを開始する人々。会社設立者やスタートアップ経営者などが含まれます。 |
| Unemployed(失業者) | 現在仕事を探しているが、職についていない人々。 |
| Housemaid(家政婦) | 家事や掃除、子育てなどを主に家庭内で行う労働者。 |
| Student(学生) | フルタイムで学業に従事している人々。大学生、高校生などが含まれます。 |
欠損値の確認
欠損値が含まれている場合モデルの学習の際に悪影響を及ぼす可能性があります。またモデルによっては、欠損値が含まれている場合うまく動作しないこともあります。
欠損値が確認された変数のみ以下のテーブルにまとめています。
なお、目的変数には欠損値は含まれていませんでした。
| 変数名 | 欠損値の数 | 欠損値の割合 |
|---|---|---|
| job | 288 | 0.006370 |
| education | 1857 | 0.041074 |
| contact | 13020 | 0.287983 |
| poutcome | 36959 | 0.817478 |
欠損値の扱いについて
job, education
jobもしくはeducationが欠損しているカラム数は2,018であり、全体の4.46[%] が欠損していました。全体の影響は少ないと考えjob, educationが欠損しているレコードは全て削除することとします。
job, educationの欠損値を削除するとレコード数は43,193rows, 17columns となります。(目的変数をjoinしたためカラム数が増えています。)
ここでデータフレームが更新されました。
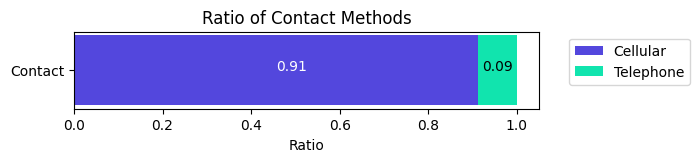
contact
contactは、全体の28.4[%]が欠損しています。contactは
- nan
- cellular
- telephone
の3種類です。
こちらの割合を見るとCellularが91[%]で、Telephoneが9[%]であることが分かります。
この割合に応じて補完する場合はCellularとTelephoneでそれぞれどんな特徴があるか確かめたのち慎重に補完する必要があります。
例えば、電話でのコンタクトを取った場合は高齢者が多いという仮説が立てられます。このような仮説をいくつか立てているとかなり時間的コストがかかります。
またcontactが欠損しているレコードを削除した場合でも30,907レコードが残ります。十分なレコードが保持できているとし、今回は削除することとします。
poutcome
poutcomeは全体の81.7[%]が欠損していることがわかりました。実際はどういう扱いをするべきか相談することがベストですが、今回は相談するべき相手がいないためpoutcomeカラムは削除することとします。
欠損値の削除後のデータフレームは30,907rows, 16columnsとなっております。
異常値の確認
欠損値処理後
欠損値処理後の状態をみて異常値がないかと確かめていきます。
df.describe(include='all')
| | age | job | marital | education | default | balance | housing | loan | contact | day_of_week | month | duration | campaign | pdays | previous | y |
|:-------|---------:|:-----------|:--------|:----------|:--------|---------:|:--------|:------|:----------|------------:|:------|---------:|---------:|------:|---------:|:-----|
| count | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907 | 30907|
| unique | nan | 11 | 3 | 3 | 2 | nan | 2 | 2 | 2 | nan | 12 | nan | nan | nan | nan | 2 |
| top | nan | management | married | secondary | no | nan | no | no | cellular | nan | jul | nan | nan | nan | nan | no |
| freq | nan | 7329 | 18379 | 16004 | 30397 | nan | 15564 | 25787 | 28213 | nan | 6336 | nan | nan | nan | nan | 26394|
| mean | 40.9189 | nan | nan | nan | nan | 1425.76 | nan | nan | nan | 15.9673 | nan | 260.485 | 2.75132 | 55.9448| 0.80849 | nan |
| std | 10.9226 | nan | nan | nan | nan | 3190.97 | nan | nan | nan | 8.22674 | nan | 257.784 | 2.95441 |112.727| 2.70617 | nan |
| min | 18 | nan | nan | nan | nan | -8019 | nan | nan | nan | 1 | nan | 0 | 1 | -1 | 0 | nan |
| 25% | 32 | nan | nan | nan | nan | 80 | nan | nan | nan | 9 | nan | 104 | 1 | -1 | 0 | nan |
| 50% | 39 | nan | nan | nan | nan | 473 | nan | nan | nan | 16 | nan | 181 | 2 | -1 | 0 | nan |
| 75% | 48 | nan | nan | nan | nan | 1502.5 | nan | nan | nan | 21 | nan | 322 | 3 | 10 | 1 | nan |
| max | 95 | nan | nan | nan | nan | 102127 | nan | nan | nan | 31 | nan | 4918 | 50 | 871 | 275 | nan |
balanceで少々怪しい値が確認されます。
こちらについての考察を進めていきます。
balance
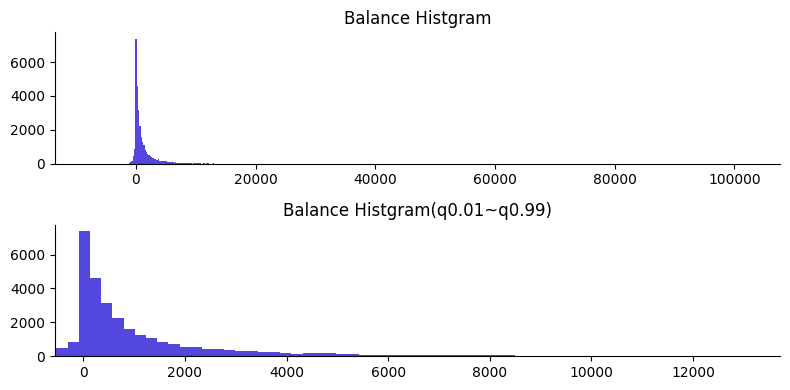
まずはbalanceのヒストグラムを可視化して全体の分布を確認したいと思います。
Balance Histgramはbalance全体のヒストグラムをプロットしています。全体から大きく外れた値があるため、図が見にくくなってしまっています。そのため、全体の1%~99%のデータのみに着目して可視化した図をBalance Histgram(q-0.01~q0.99)として表示しています。
balanceは年間平均残高を示しています。そのため負数であるということは、借金があるとします。
全体の値から大きく外れている値は削除しません。このような外れ値は、極端に貯金がある人や極端に借金がある人だと考えられます。不自然な数値ではないため今回は外れ値の除去はせずに分析を進めていきます。
また、balanceは0以上の値であればsaving(貯金カラム)、0より小さい値でればdebt(借金カラム)として新たなカラムに代入します。
条件に当てはまらない場合はnullを代入しておきます。
ちなみに、pdaysについて
pdaysは前回のキャンペーンで最後に顧客とコンタクトを取ってから経過した日数を示しています。
pdaysカラムの-1は、データ元の説明から前回のキャンペーンではコンタクトを取らなかったとわかります。
データの可視化
いくつかのカラムをピックアップして可視化を行います。
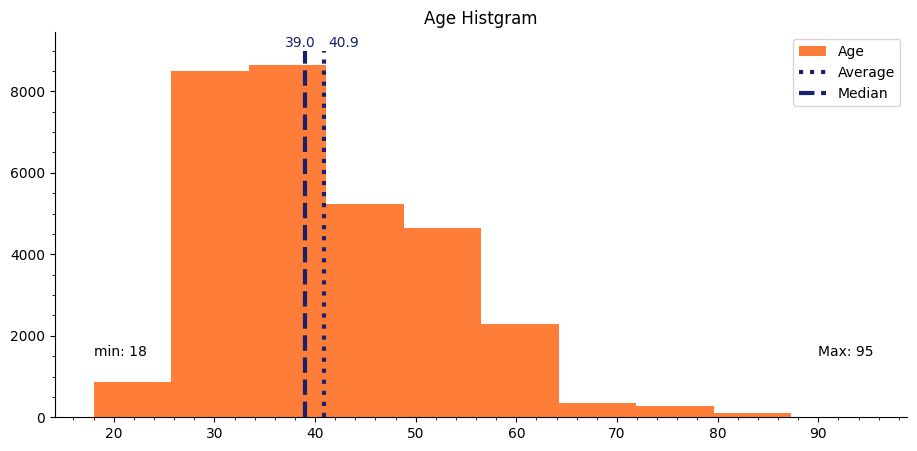
Age Histgram
年齢を見ると18~95歳までのレコードが確認できます。また、平均年齢は40.9歳、中央値は39歳だと示されています。
一般的に働く年齢のデータが多い傾向だという印象を受けます。
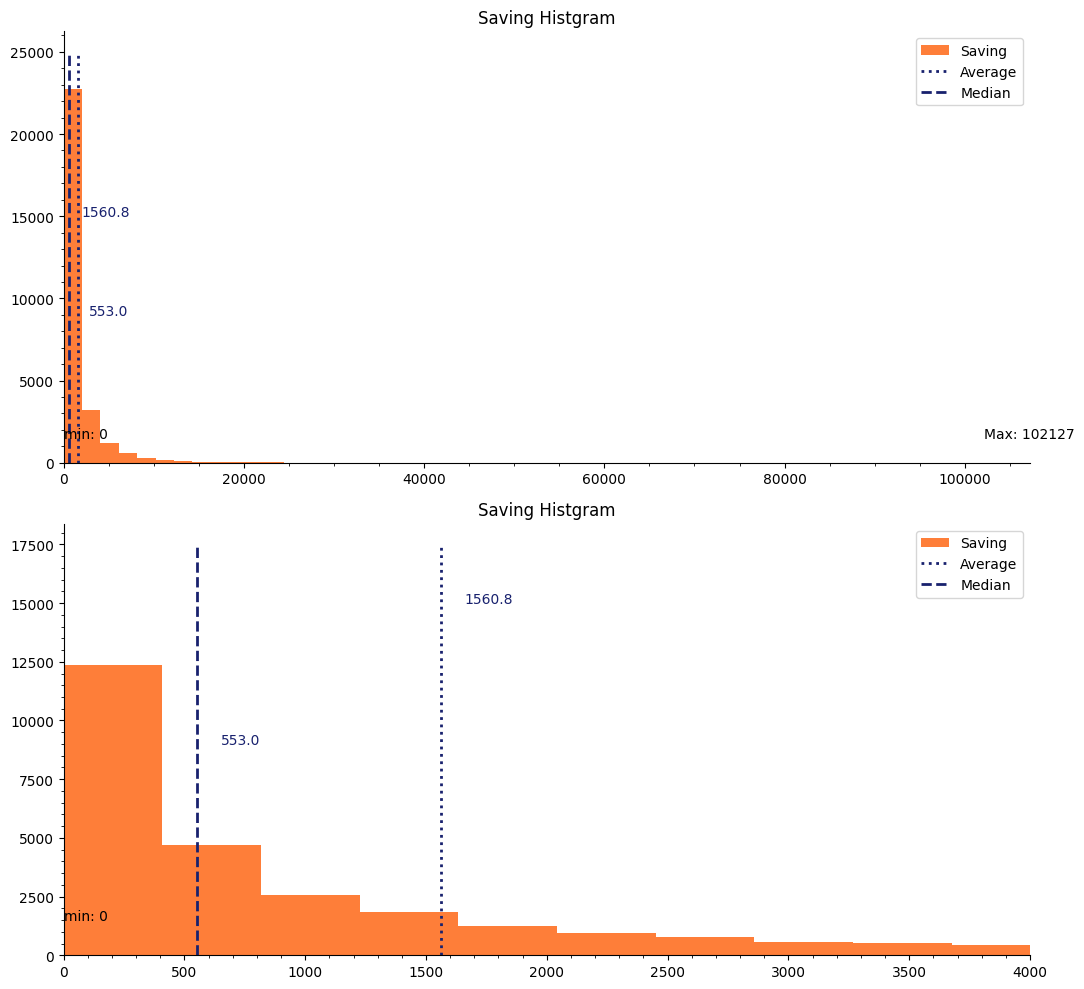
Saving Histgram
年間平均残高のヒストグラムを可視化しました。上は全体を表示したもので、下は横軸を10,000を最大値として左側に注目した図です。(xlimを使用しています。)
最小値は0ユーロで、最大値は103,127ユーロです。また平均値は1,560.8ユーロで、中央値は553ユーロをです。最大値に引っ張られて平均値が中央値よりも大きくなっていることがわかります。
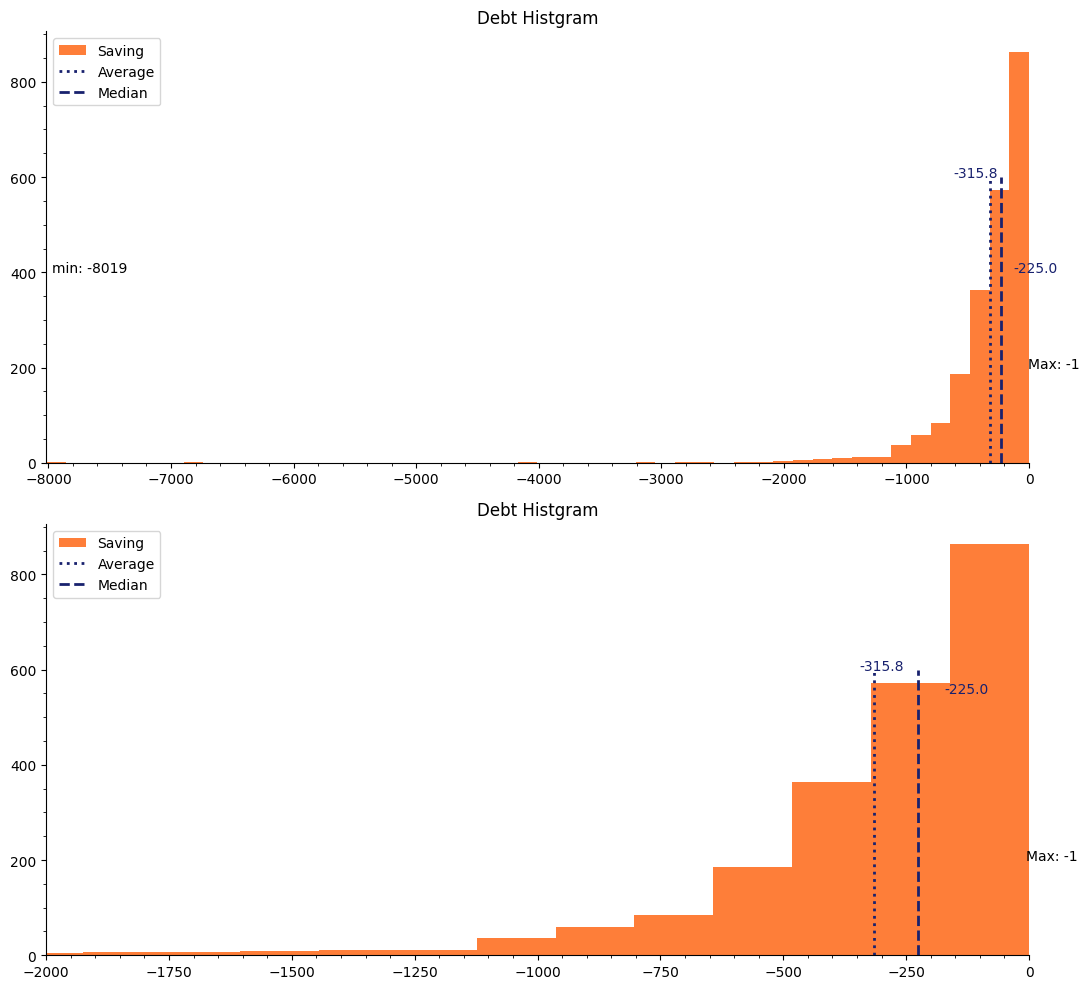
Debt Histgram
次に年間平均借金のヒストグラムを可視化しました。上下の図については、Saving Histgramと同様です。
最小値が-8,019ユーロ、最大値が-1ユーロです。平均値は-315.8ユーロ、中央値が-225ユーロです。
モデリング
今回の目的は、顧客が定期預金に申し込むかどうかの分類問題の2値分類です。
そのため今回作成するモデルは以下のものを試します。
- 決定木
- ランダムフォレスト
- LightGBM
データ分割法
全体のデータを10とした場合、訓練データ・検証データ・テストデータをそれぞれ6:2:2の比率で分割しました。
決定木
決定木では、モデルの解釈性が高いという特性があります。そのため、考察を簡単に行うため、決定木の分類状態を可視化する際は、max_depthを固定します。ただし、学習の際にはmax_depthは与えません。また、ハイパーパラメータのチューニングは、今回は行いません。
加えて、他のモデルと比較のため、訓練データのレコード数は統一させたいです。よって、決定木で使用するデータは訓練データとテストデータのみとします。
durationについて
durationは、説明変数に加える場合は強く目的変数に対して寄与してしまいます。現実的なモデルを作成するには、このカラムを削除する必要があります。
データ元の説明と、それを翻訳したものを下記に示します。
last contact duration, in seconds (numeric). Important note: this attribute highly affects the output target (e.g., if duration=0 then y='no'). Yet, the duration is not known before a call is performed. Also, after the end of the call y is obviously known. Thus, this input should only be included for benchmark purposes and should be discarded if the intention is to have a realistic predictive model.
最終接触時間、秒単位(数値)。 重要:この属性は出力対象に大きく影響する(例えば、duration=0の場合、y='no')。 しかし、持続時間は、callの実行前にはわからない。 また、通話終了後のyは明らかに既知である。 したがって、この入力はベンチマークのためにのみ含めるべきであり、現実的な 予測モデルを持つことを意図している場合は破棄すべきである。
決定木の結果
durationを含めた決定木と、含めない決定木の比較
こちらはdurationを含めた決定木です。
Test Accuracy: 0.84
precision recall f1-score support
False 0.91 0.91 0.91 5288
True 0.46 0.46 0.46 894
accuracy 0.84 6182
macro avg 0.69 0.68 0.68 6182
weighted avg 0.84 0.84 0.84 6182
次にdurationを含めない決定木です。
max_depthが3では、分類しきれていない部分が多かったため4の場合をプロットしました。
Test Accuracy: 0.79
precision recall f1-score support
False 0.88 0.87 0.88 5288
True 0.29 0.31 0.30 894
accuracy 0.79 6182
macro avg 0.59 0.59 0.59 6182
weighted avg 0.80 0.79 0.79 6182
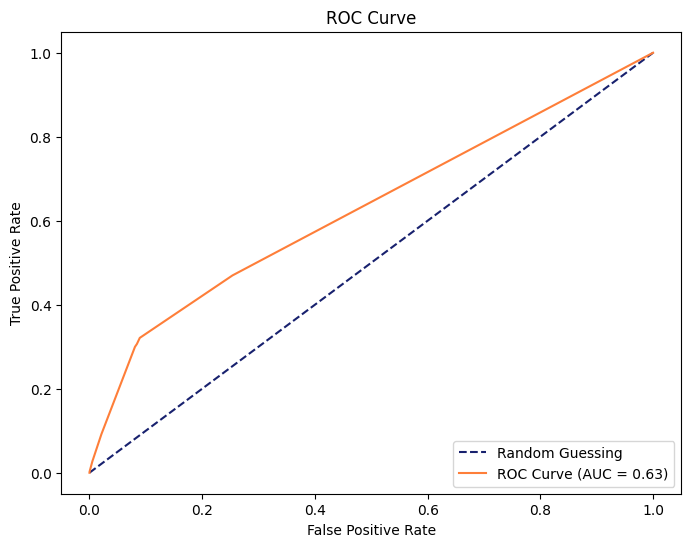
durationを含めない場合のROC曲線をプロットしてみます。
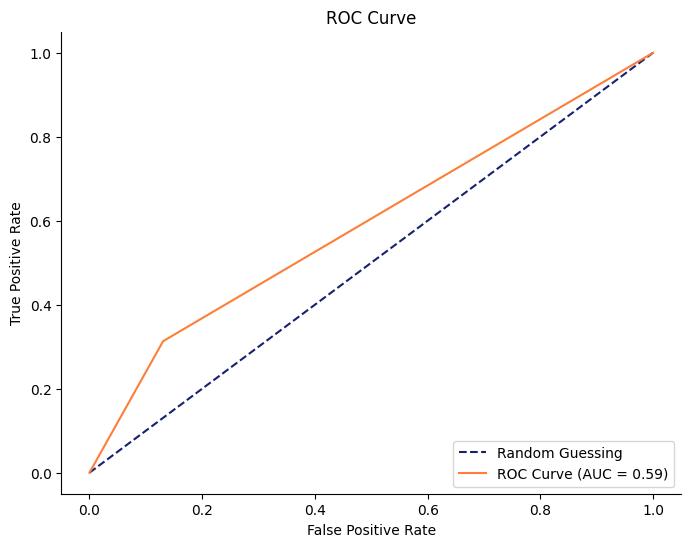
また決定木が目的変数を予測するのに、重要な特徴量を可視化してみます。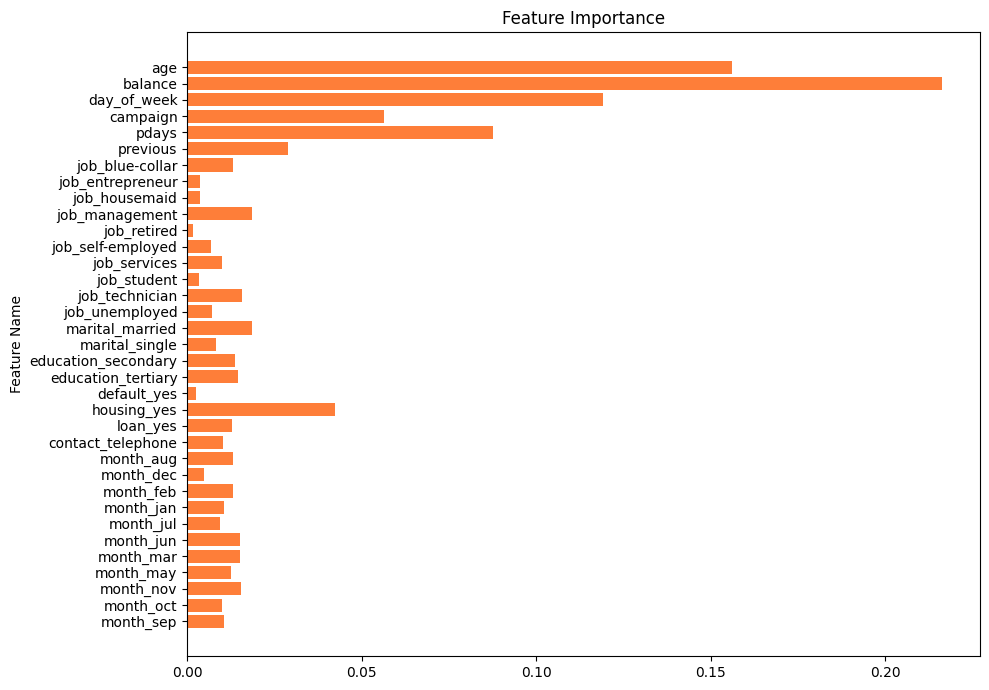
こちらは縦軸に特徴量、横軸にはどれほど重要であるかの指標が可視化されています。また、横軸の値は相対的な数値で、特徴量同士の比較のみに用います。
得られる示唆
durationを含めた決定木では、最初にdurationの値に注目しているところから、durationは注意事項にあるように正解データに対して強く貢献するようです。
durationを含めない決定木は、現実的なモデルではないためこれ以上の考察は行いません。
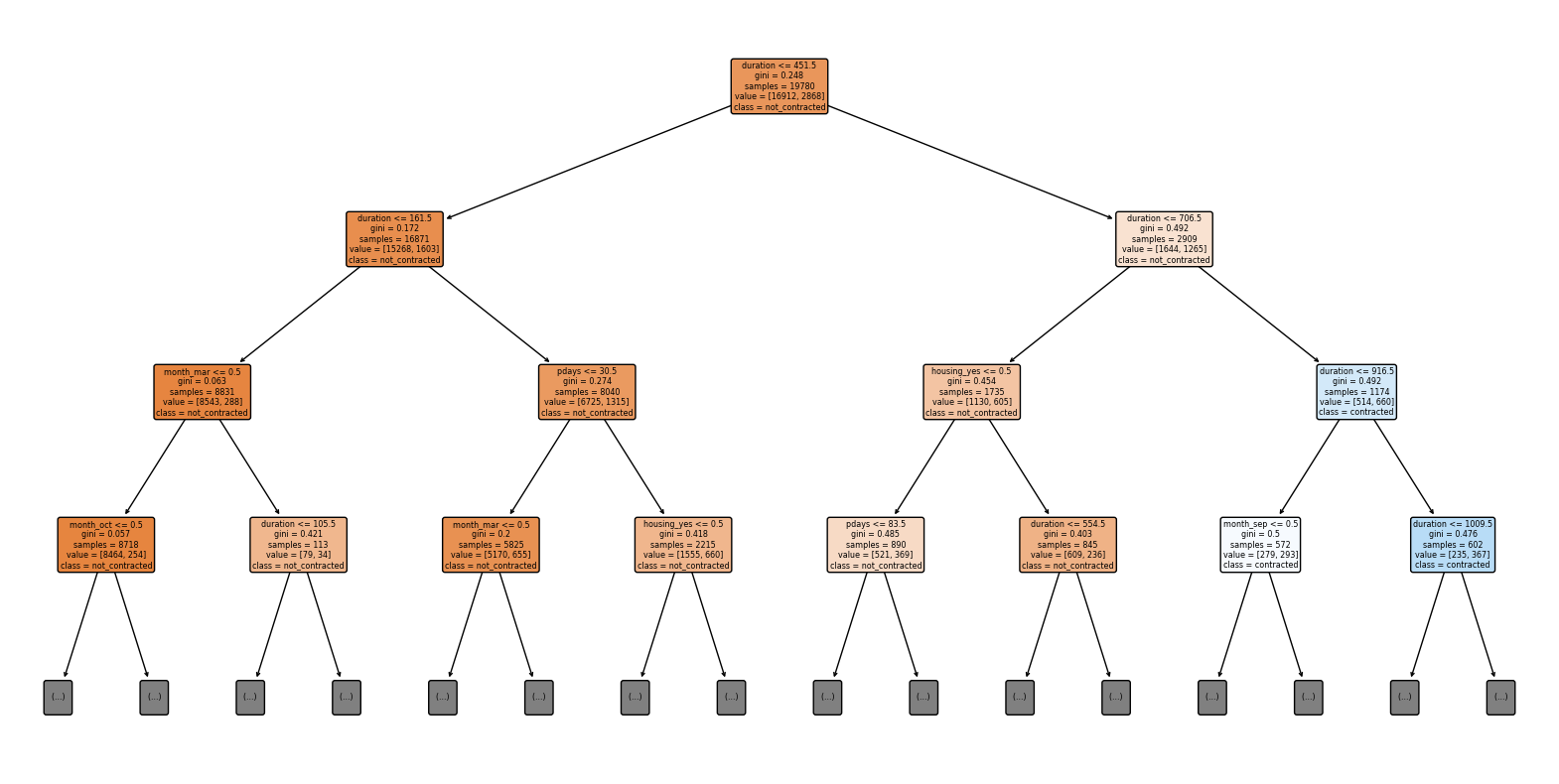
次にdurationを含めない決定木です。定期預金に申し込む場合があると予想されている葉ノードの中で、ジニ係数が0.45以下のものを取り上げます。
patern1
- 年齢が60.5歳以下である
- 顧客が前回のキャンペーンで最後にコンタクトをとってから経過した日数が、8.5日以下である
- 3月である
- マネジメント職ではない
もしくは、patern2
- 年齢が60.5歳よりも上である
- 最後に連絡した日が、7.5日より小さい(1週間以内)
- 最後に連絡した月が、5月である
- 貯金が1,183ユーロ以下である(借金を含む)
または、patern3
- 年齢が60.5歳よりも上である
- 最後に連絡した日が、7.5日より大きい(1週間以上経過)
- 最後に連絡した月が、8月である
- 住宅ローンがある
patern2に注目してみます。
年齢が60.5より上ということは仕事を退職したと考えられます。また最後に連絡してから1週間以内であり、コンタクトを取ってから時間が経ちすぎない場合の方が、定期預金申し込みが期待できることが分かります。
最後に連絡した月が5月である理由を突き止めるには、ドメイン知識が求められそうです。
貯金が1,183ユーロ以下の人は定期預金に申し込む傾向があるようです。
仕事をリタイアしていて、貯金が少ない場合は定期預金に申し込むようですね。もしかすると、再雇用されていて定期預金の案内が最近あったため定期預金に申し込んだかもしれません。
定期預金を申し込む人物の属性が具体的にイメージしやすいことが、決定木の最大のメリットかなと感じます。
解釈性の高い決定木では、モデルの精度に加えて人間の直感や経験を組み合わせることが可能です。
ビジネスでは、ペルソナを想像しやすい長所があります。一方で、コンペでは精度で劣るため採用されることは少ないようです。
AUCが0.59とランダムよりは優れているものの、このモデルは改善の余地がありそうです。ただ、特徴量エンジニアリングは沼なので今回はこれ以上の性能は求めないこととします。
ランダムフォレスト
決定木と同様に、使用するデータはtrain dataとtest dataです。
ランダムフォレストでは、rando_state=0と固定し、その他のパラメータはデフォルトのままとしました。
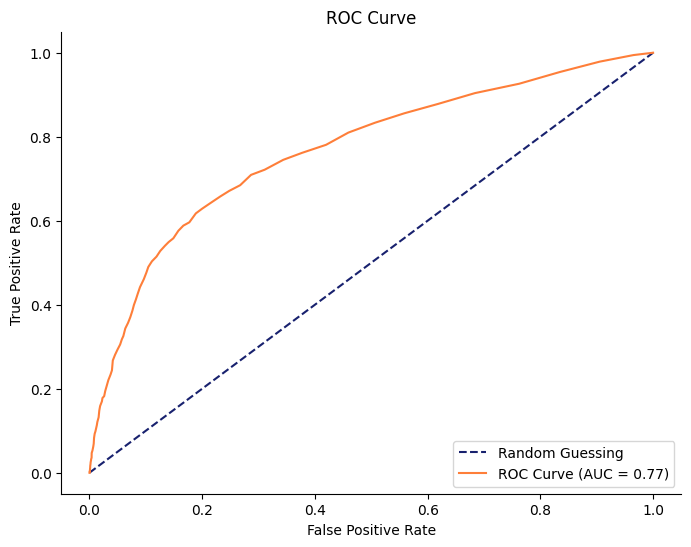
ランダムフォレストの結果
Test Accuracy: 0.86
precision recall f1-score support
False 0.88 0.97 0.92 5288
True 0.54 0.19 0.29 894
accuracy 0.86 6182
macro avg 0.71 0.58 0.60 6182
weighted avg 0.83 0.86 0.83 6182
ランダムフォレストは解釈性よりも、精度を重視したモデルです。
そのため決定木よりも高い精度が発揮されていることがわかります。
次に実装するLightGBMというモデルとの処理時間を比較するため、計算時間を表示しました。
結果は、1.20[sec] でした。
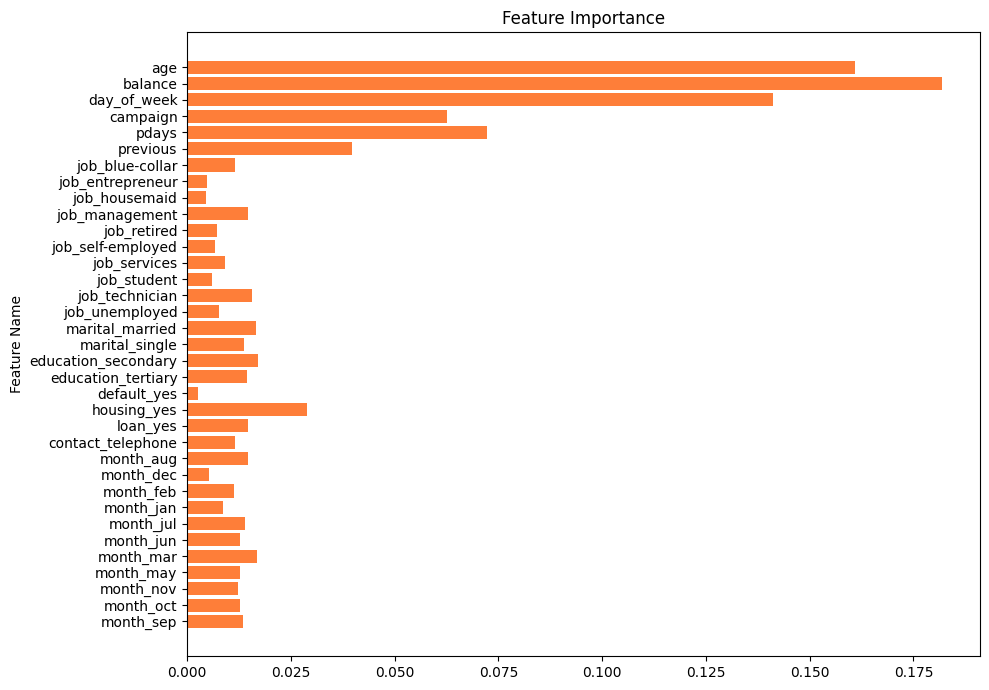
重要な特徴量を調査する
重要な特徴量は、決定木の時とあまり変わりませんでした。
特徴量の順番は変更されていません。
定期預金に申し込むかどうかを判断するには、
- age
- balance
- day_of_week
が重要となるようです。
簡単に上記の特徴量について考えてみます。
預金するかどうかは年齢が大きな判断材料となるようです。これは、ライフステージによって必要になるお金が変わるためだと考えられます。
年間平均残高は、最も大きな判断材料になることが分かります。例えば、現状で貯金ができないような人は、しばらくは貯金する余裕がないため、定期預金に申し込まなさそうです。また、極端に貯金がある人は銀行に預金ではなく、投資運用に回す可能性があります。そのため、おおよそ年間平均残高が中央値に近い人ほど、定期預金に申し込みそうです。
day_of_weekに関して、最後にコンタクトを取ってから、あまり日数が経過していない人と、長期間リアクションがなかった人を比べると定期預金に申し込む可能性に差がありそうです。
LightGBM
LightGBMは勾配ブースティング決定木の一種です。特に計算スピードと、計算に使うメモリを小さくする工夫が施されていますLightGBM A Highly Efficient Gradient Boosting
Decision Tree。
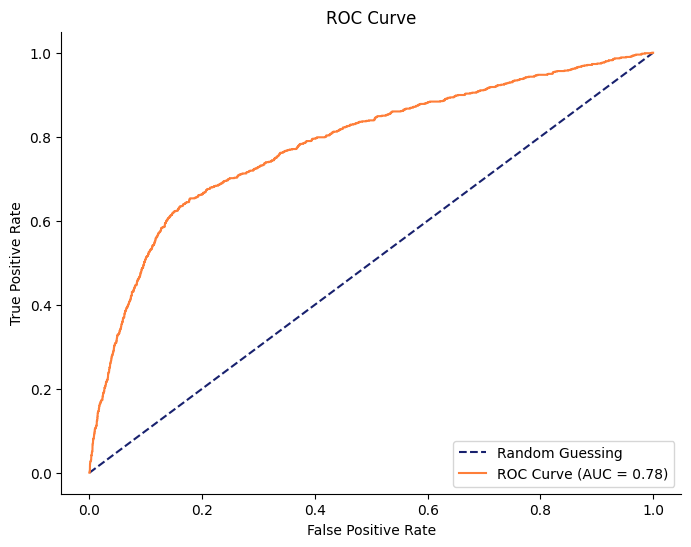
LightGBMの結果
Test Accuracy: 0.86
precision recall f1-score support
False 0.88 0.97 0.92 5288
True 0.56 0.20 0.30 894
accuracy 0.86 6182
macro avg 0.72 0.59 0.61 6182
weighted avg 0.83 0.86 0.83 6182
結果はランダムフォレストの時と大きな差は見られません。
計算時間は0.09[sec] でした。ランダムフォレストと比較して、おおよそ1.11[sec] 短縮されています。
LightGBMは、計算コストとメモリの省略に関して工夫が施されているモデルで、精度に関しては大きく向上することが期待されていません。
そのため、このようにランダムフォレストより、計算による時間は短縮されたものの精度に関しては大きく変わらない結果になったと考えられます。
また、LightGBMは欠損値を含んでいても学習を行えるメリットを持っています。
しかし、今回のデータは欠損値が含まれておらず、ランダムフォレストの計算時間も1秒程度であったため、LightGBMを採用する旨味は少ないかなと思われます。
まとめ
概要に載せた表と同じものになります。
| Model | Accuracy | AUC | Calculation Time |
|---|---|---|---|
| Decision Tree | 0.79 | 0.59 | - |
| Random Forest | 0.86 | 0.77 | 1.20 sec |
| LightGBM | 0.86 | 0.78 | 0.09 sec |
精度に関しては、決定木<ランダムフォレスト≦LightGBMという結果になりました。
純粋に精度だけを求めるのであれば、ランダムフォレストやLightGBMが採用されやすく、解釈性を求めるのであれば決定木が採用されやすいことにも納得です。
ビジネスのような意思決定を行う際に、解釈性の高いモデルも採用する場面がしばしばあるのではないかと思います。
特にモデルと人間の意思決定を融合させたい場合では、解釈性の高い決定木が採用されやすいのかなと思います。
今回は教科書レベルの知識が確認できる経験が得られたと思います。
付録
決定木の精度を高めてみる
重要な特徴量を調べ、そうでない特徴量を除去をして学習させました。
不要な特徴量を除去するだけで、ACUが0.4pt向上しました。
durationを含めたランダムフォレスト
Test Accuracy: 0.88
precision recall f1-score support
False 0.91 0.96 0.93 5288
True 0.63 0.41 0.50 894
accuracy 0.88 6182
macro avg 0.77 0.68 0.71 6182
weighted avg 0.87 0.88 0.87 6182
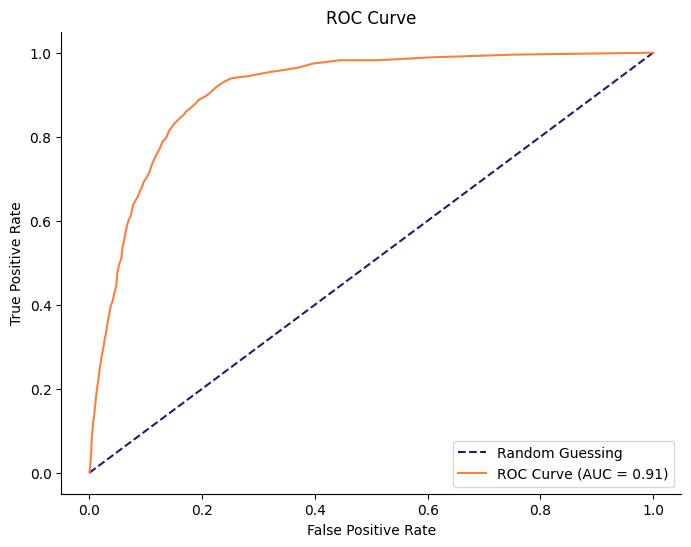
言わずもがなですが、durationを特徴量に含めるとAUCが向上します。とはいえ、実際に現場では得られないカラムになるため、一概に良いモデルとは言えません。