計算式プラグインで、スペース項目にサイン波を表示してみます。
概要
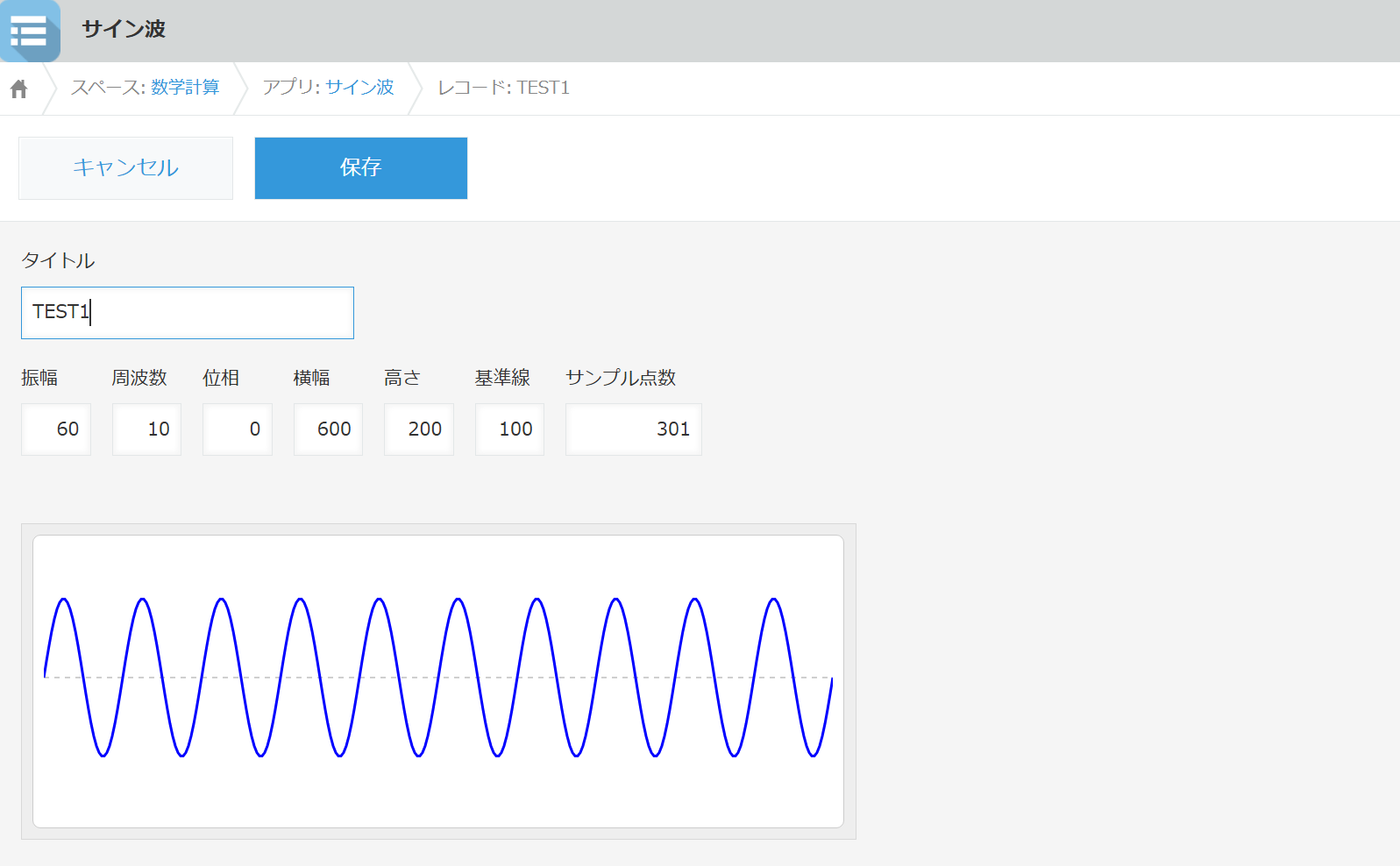
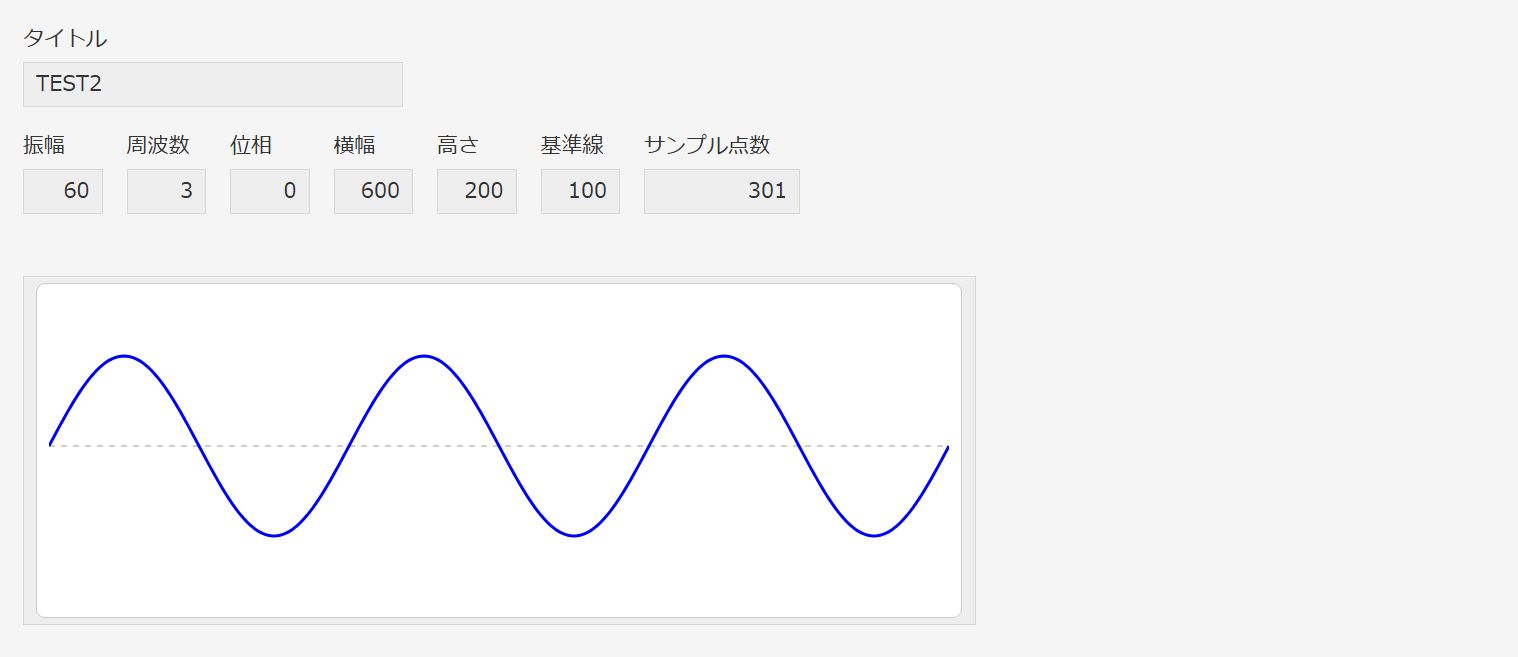
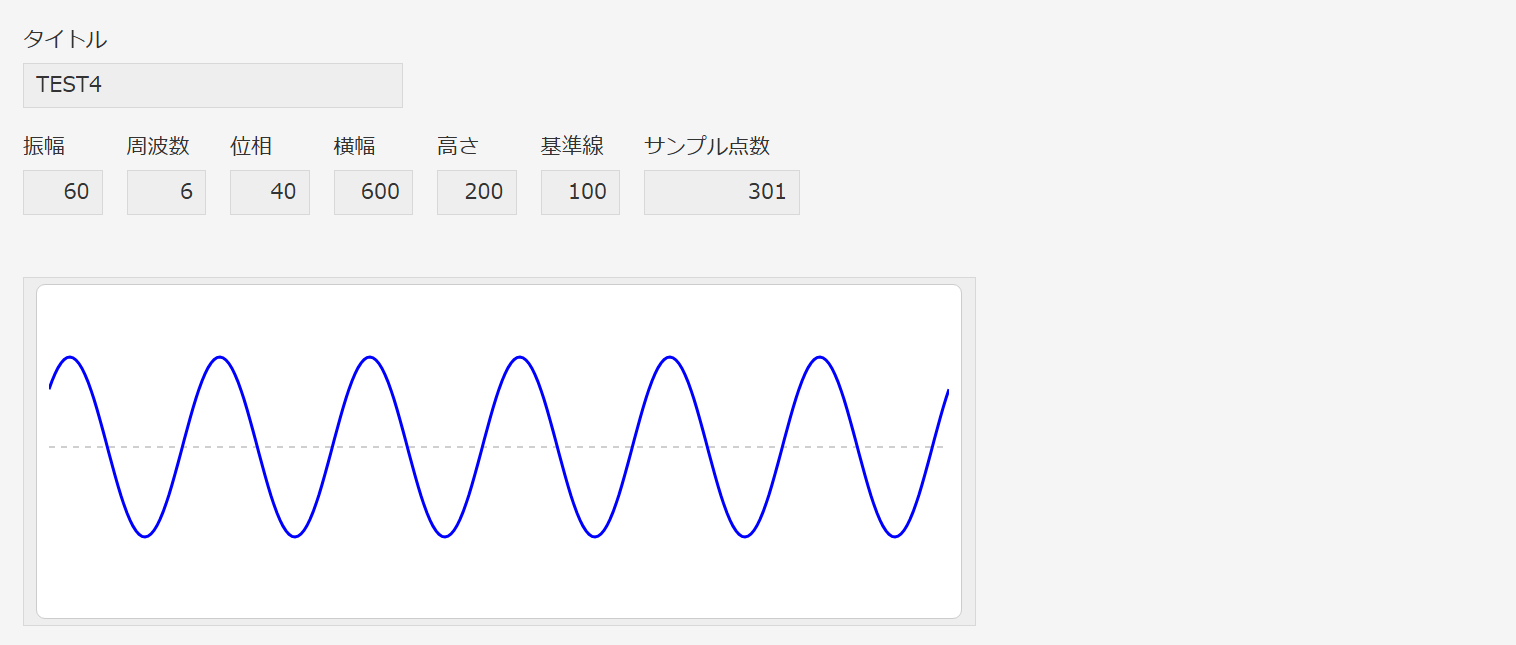
振幅、周波数等を与えて、スペース項目にSVGでサイン波を表示します。
計算式プラグインで、SVG タグを組み立てます。
パラメータ説明
| 項目 | 役割 | 指定例 | 備考 |
|---|---|---|---|
| 振幅 (A) | 波の高さ(px) | 40 | 大きいほど上下に大きく振れる |
| 周波数 (FREQ) | 1 幅あたりの波の回数 | 1 | 2 にすると 2 波入ります |
| 位相 (PHASE) | 度数法の位相シフト | 0 | 90 で 1/4 周期シフト |
| 横幅 (W) | SVG 幅(px) | 600 |
viewBox と一致 |
| 高さ (H) | SVG 高さ(px) | 200 |
BASE の基準に利用 |
| 基準線 (BASE) | 0 ラインの Y 座標 | 100 | 下に行くほど値が大きい(SVG座標) |
| サンプル点数 (N) | 折れ線の分解能 | 200 | 多いほど滑らか(描画負荷↑) |
補足:
M_SINは 度数法で角度を受け取ります。式内ではM_RADで度→ラジアンに変換し、(x/W)*360*FREQ + PHASEを角度として使っています。
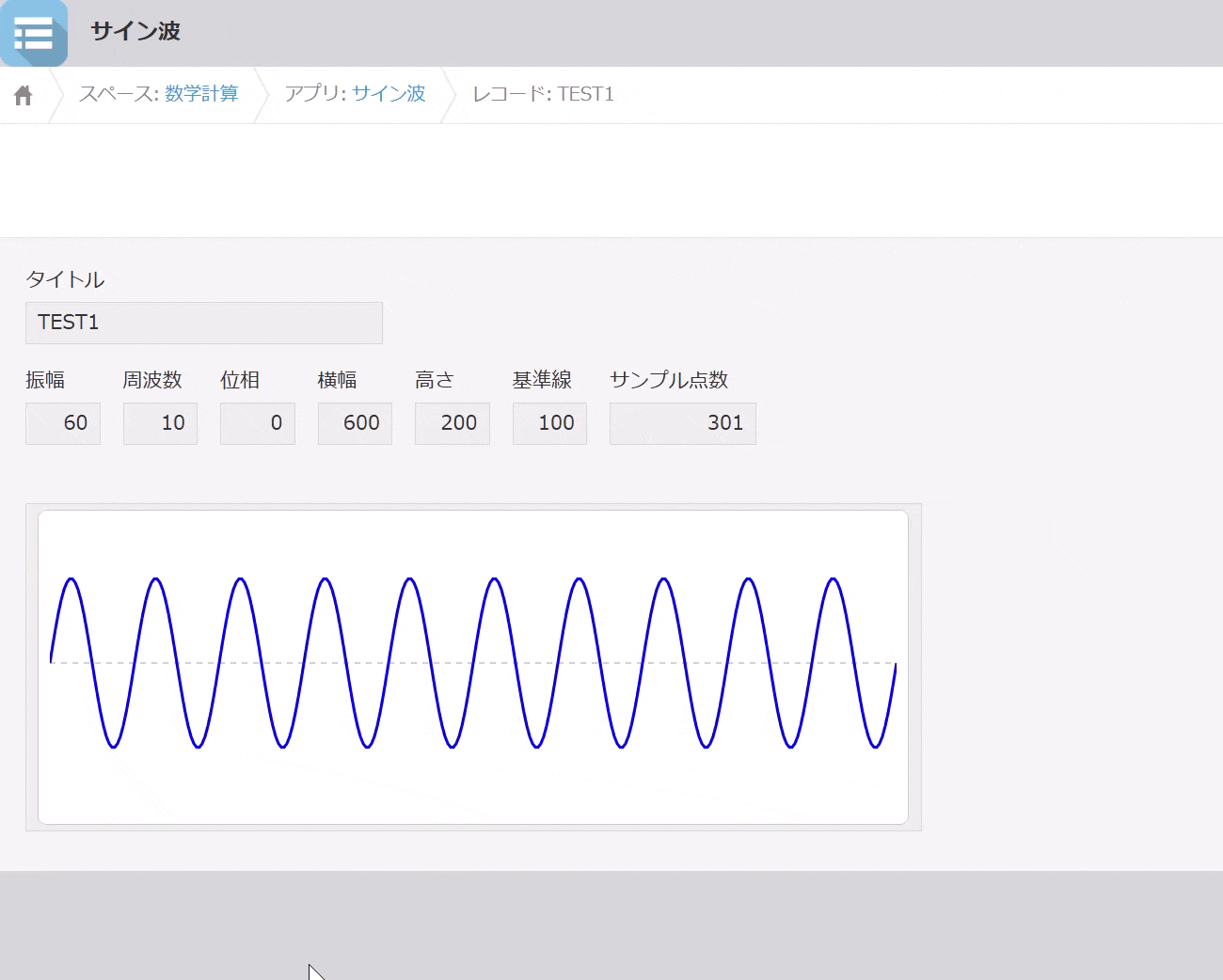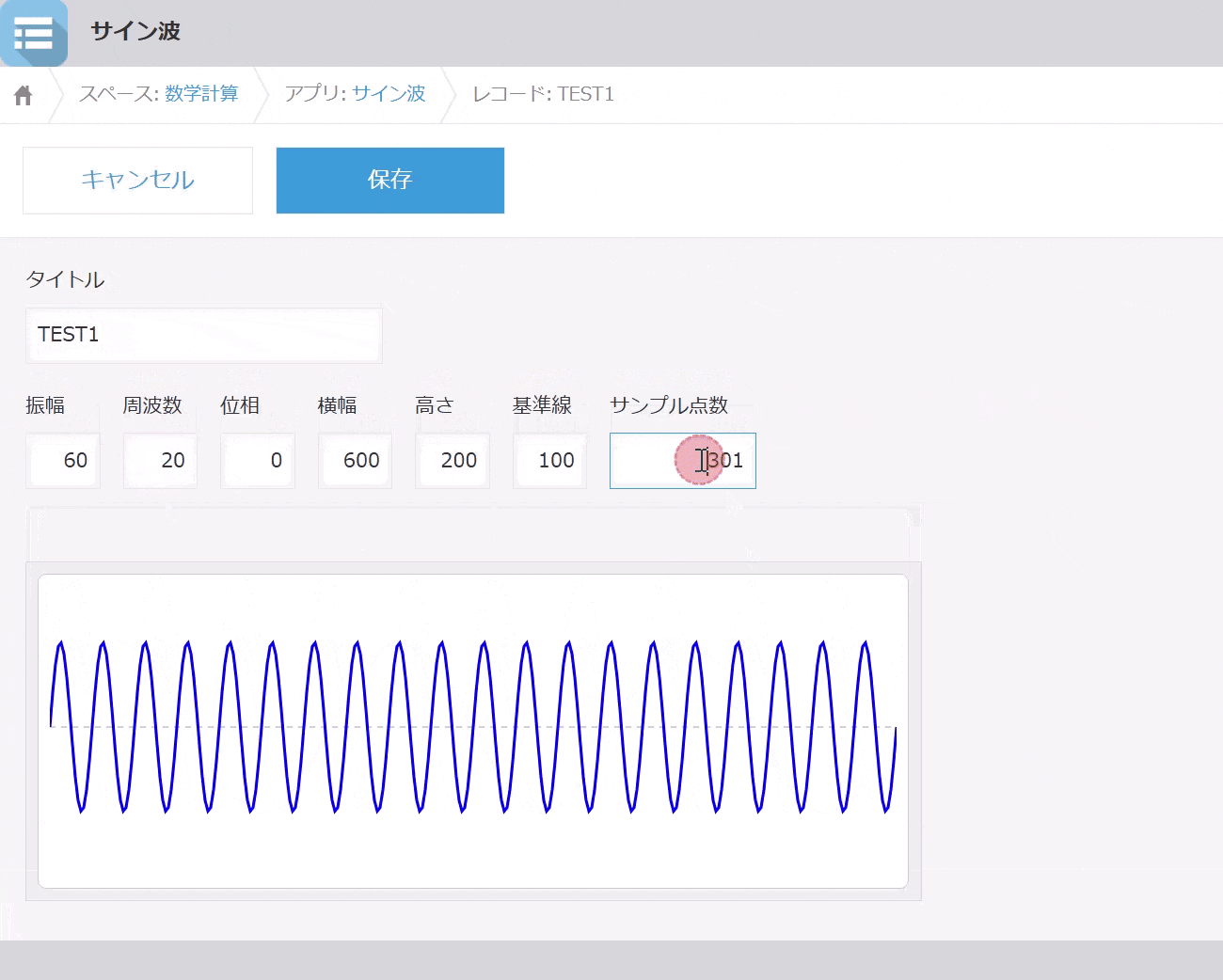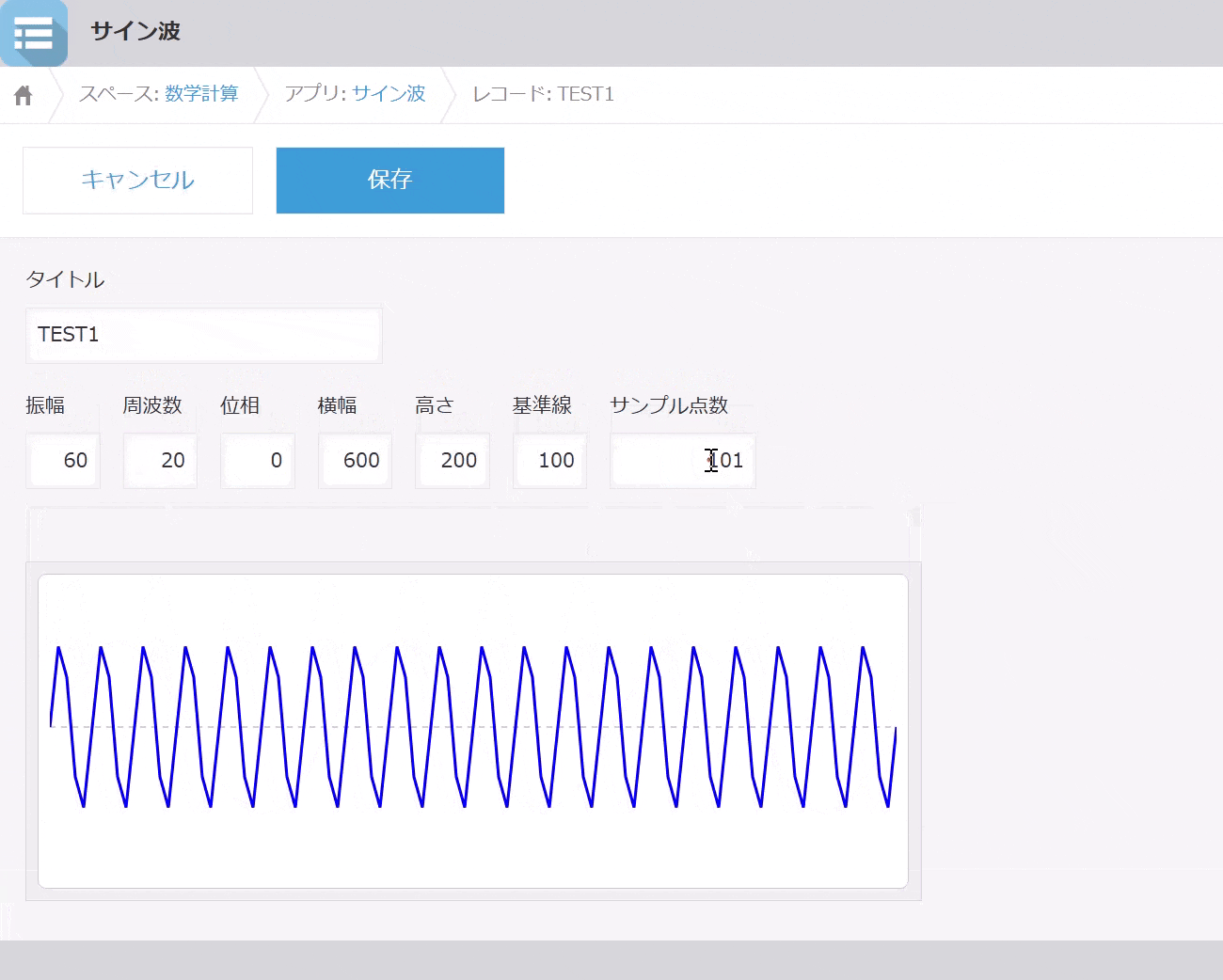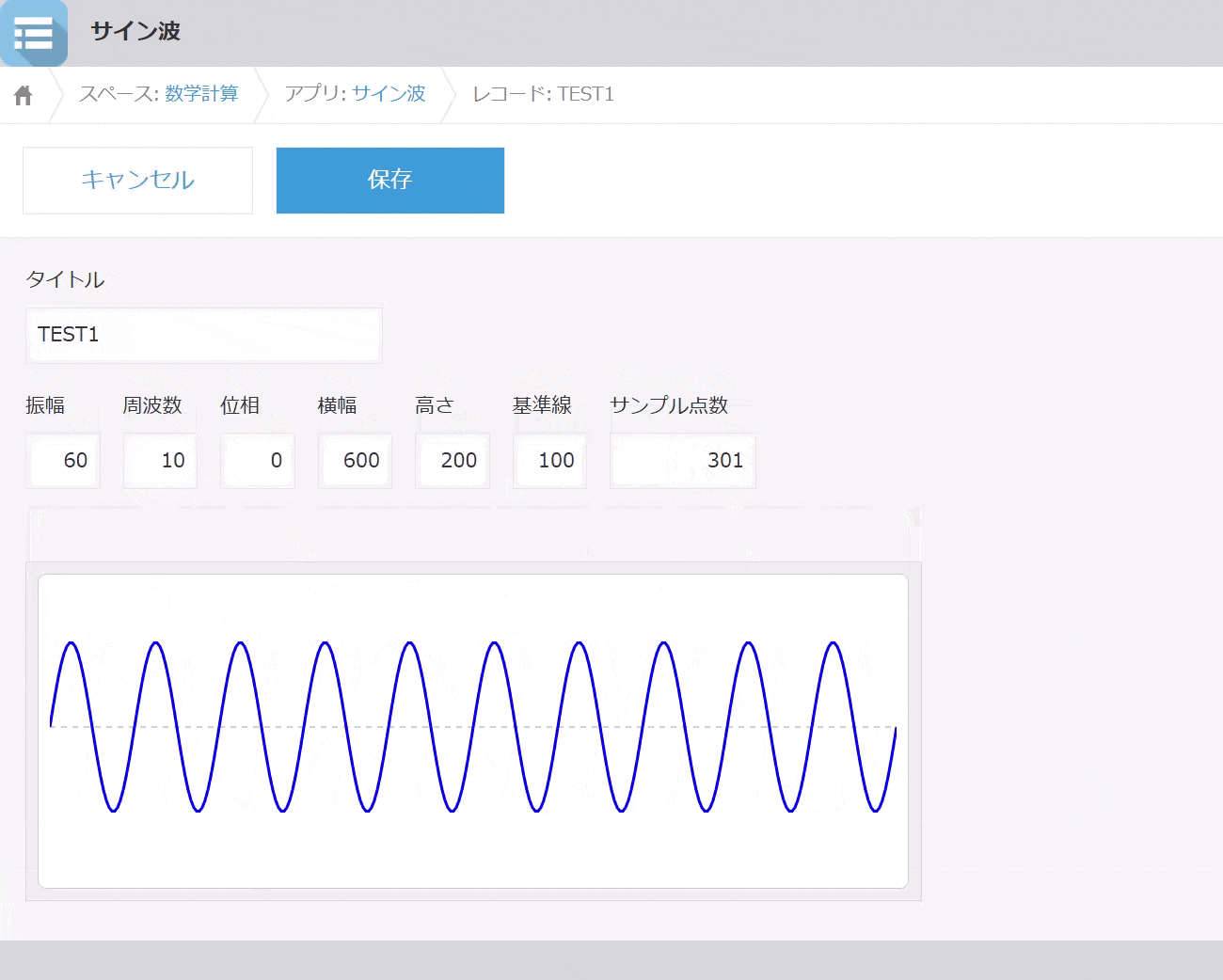
表示例
操作例
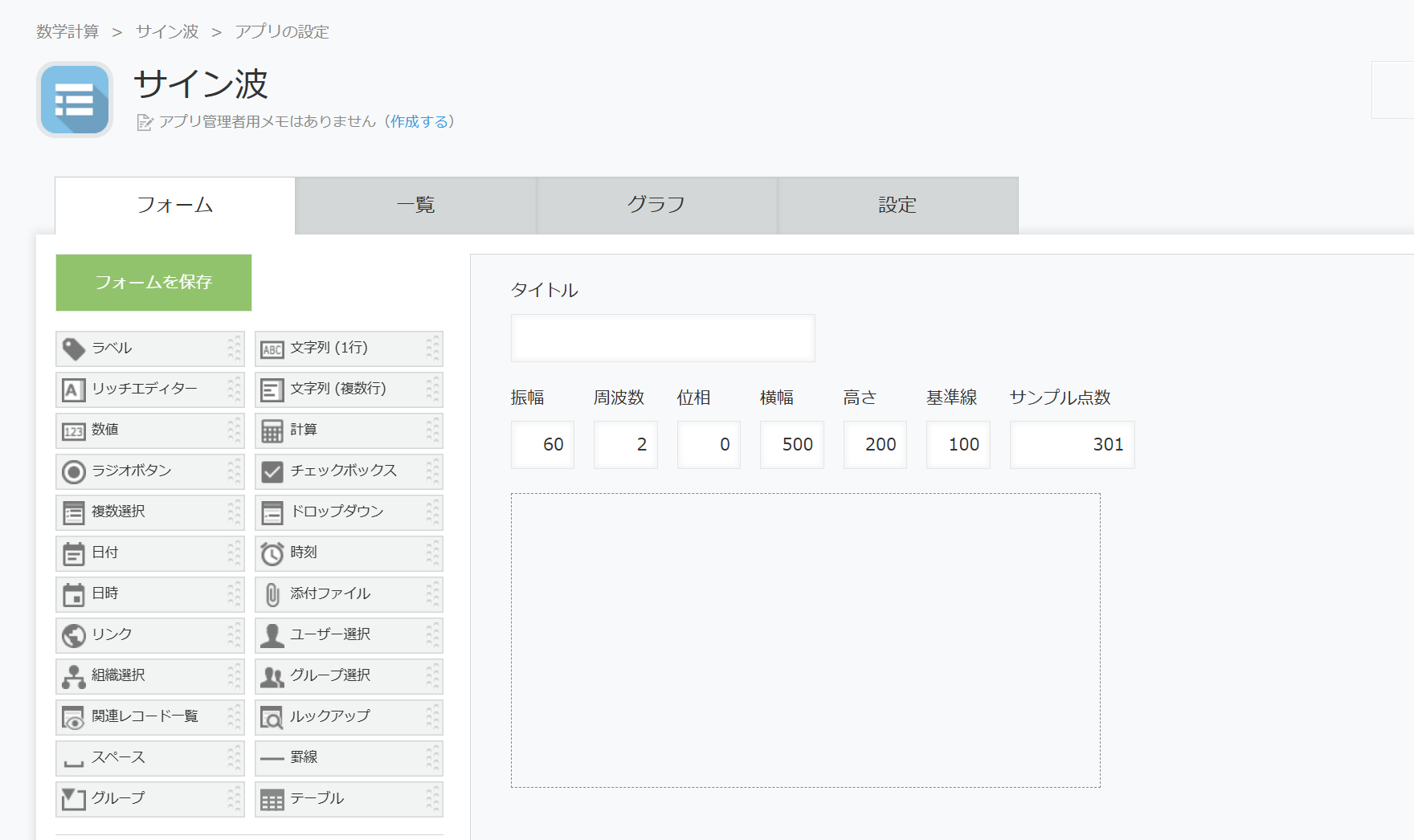
アプリ設定
スペース項目を配置して要素ID「sp1」をセット
計算式プラグイン設定
スペース項目に計算式を設定します。
OPTION: 非同期計算
// sp1:(sp1) SPACER
// サイン波
LET(
A, 振幅,
FREQ, 周波数,
PHASE, 位相,
W, 横幅,
H, 高さ,
N, サンプル点数,
BASE, IF(基準線 > 0, 基準線, 高さ / 2),
POINTS, JOIN(
ARRAY_FOR(N, i,
LET(
x, (W * i) / (N - 1),
y, BASE - (A * M_SIN(M_RAD((x / W) * 360 * FREQ + PHASE))),
x & "," & y
)
),
" "
),
STYLE, TAG("style", JOIN(ARRAY(
".sine-wrap{display:inline-block;background:#fff;border:1px solid #ccc;padding:8px;border-radius:6px;}",
".sine-axis{stroke:silver;stroke-dasharray:4 4;}",
".sine-line{fill:none;stroke:blue;stroke-width:2;}"
), NEWLINE(), 1)),
SVG, TAG("svg",
ATTR(
"xmlns","http:/"&"/www.w3.org/2000/svg",
"width",横幅,"height",高さ,
"viewBox","0 0 " & 横幅 & " " & 高さ
),
TAG("rect", ATTR("x","0","y","0","width",横幅,"height",高さ,"fill","white")),
TAG("line", ATTR("class","sine-axis","x1","0","y1",BASE,"x2",横幅,"y2",BASE)),
TAG("polyline", ATTR("class","sine-line","points",POINTS))
),
TAGS_HTML(ARRAY(STYLE, TAG("div", ATTR("class","sine-wrap"), SVG)))
)