アメリカ大学院の数理最適化授業で扱う内容まとめ

はじめに

どうも、梅田と申します。

数理最適化を生業にしている変な珍しい会社のグリッドという会社でひっそりと働いてます。色々役割担ってきましたが、今は営業を主に担当しています。

現在、Georgia Techという大学の、Computer Scienceの大学院修士課程に属してます。
「お前は何もわかってないから大学で勉強し直してこい！」と所属する会社で毎度大学院にぶち込まれ、実は人生3回目の修士課程です。Master of Masterだね、ってよくいじられます。

まあそんなことはどうでもよくて、今年数理最適化の授業を選択したので、その授業内容について記します。
アメリカの大学の数理最適化の授業、一体どんなことやってるの？ってのは、もしかしたらごく一部の変態にはウケるかなと思って書くことにしました。
この授業、本業に関わるので、真剣に勉強しました。期末テスト満点！(自慢ごめん)

まあそんなことはほんとどうでもよくて、以下の流れで記事を書きます。

• 最初に大学院の紹介をします。
• どんなこと習うのか、何も例を出さないと実感湧かないと思うので、個人的に面白かったなーっ思ったトピックとして、ロバスト最適化問題を双対問題で書くとスッキリ！についてちょろっと話します。
• 最後に定式化お役立ちリンク集で締めます。

目次

• はじめに
• 大学院の紹介
  • Deterministic Optimization（授業紹介）
    • Week別カリキュラム
  • 受講してみた感想
• どんなことを習うのかの例
  • ロバスト最適化：ロバスト制約を双対で有限個の制約に落とす
• 定式化お役立ち
  • リンク集

大学院の紹介（Georgia Tech）

最初に、簡単に大学院の紹介です。

受講形式はonlineです。ですが、Georgia Techのonline修士課程、offlineの卒業生と学位の区別をしないため、わりかし人気みたいです。
ただ、そのかわりしんどい。普通にキャンパスでキャッキャしてるフレッシュキラキラ大学生と同じカリキュラムで進むので、宿題がしんどい。仕事があるとか全く考慮されてない。出張とか入るとほんと死ぬ。

Georgia Techを選んだ理由は、上記に加えて、Operations Researchのつよつよ研究者がいて彼らがレクチャーを作ってくれてること、公立で比較的学費が安いことが理由です(会社のためを考えて、ね)。

まずは最適化の授業周りの全体像から。最適化の授業はOperations Research(以下OR)という学科で習います。
OR学科のカリキュラムはこちら。

• Operations Research, MS（Georgia Tech Catalog）

習う科目は、すんごく雑に言えば、シミュレーション、最適化、統計、確率過程みたいに分けられる気がします。
今回私が受講したのは、3つあるコア科目の一つである、Deterministic Optimizationです。

Deterministic Optimization（授業紹介）

Week別カリキュラム

週ごとに「何をできるようにする週か」が分かるようにまとめました。

Week	できるようにすること（ゴール）	例 / モジュール
1	最適化の入り口を固める：最適化モデルの基本形（目的関数・制約・変数）と、最小化/最大化・連続/離散などの問題分類を整理する。 最適化の進め方を体験する：ポートフォリオ最適化を題材に「課題→定式化→解く→解釈」の一連の流れを踏む。	Module 1–2
2	数学の足場を作る：線形代数（内積・固有値/固有ベクトル・行列の性質）と、関数/集合の基本性質を復習する。 凸性を武器にする：凸関数・凸集合・凸最適化の定義を押さえ、凸であることが「解ける」「保証がある」に直結する感覚を掴む。	Module 3–4
3	最適化が“どう終わるか”を理解する：最適解の存在、局所解と大域解、改善探索（improving search）の考え方を整理する。 最適性の証明と緩和に慣れる：最適性証明（certificate）の立て方、緩和、ラグランジュ緩和と双対の入口を扱う。	Module 5–6
4	無制約最適化（微分あり）：一階/二階の最適性条件、勾配降下法、ニュートン法の「更新式の意味」と「いつ収束するか」を押さえる。 無制約最適化（微分なし）：単変数・多変数での探索（導関数が使えない状況の考え方）を学ぶ。	Module 7–8
5	線形計画（LP）のモデリング感覚を鍛える：輸送問題・最大流・最短路など、ネットワーク構造をLPとして定式化し、制約と変数の置き方を体に入れる。 実務っぽいLP：電力市場を例に、発電計画・市場清算など「現実の仕組み」を制約で表現する。	Module 9–10
6	不確実性下の意思決定：2段確率LP（two-stage stochastic LP）として「今決める/後で修正する」を定式化し、解き方の全体像を掴む。 非線形の“扱い方”：区分線形（piecewise linear）での近似、ロバスト回帰、放射線治療など、LPで非線形を受け止める技を学ぶ。	Module 11–12
7	LPの幾何を腹落ちさせる：多面体、極点（extreme point）、凸包、非有界方向（extreme ray）を通じて「なぜ頂点を探すのか」を理解する。 LPの代数（BFS中心）：基本実行可能解（BFS）と標準形、なぜBFSが重要かを整理する。	Module 13–14
8	シンプレックス法のコア：局所探索としてのLP、辺を歩く（pivot）という見方、停止条件を理解する。 実装上の論点：退化（degeneracy）、Phase I/II、例題で手順を追う。	Module 15–16
9	LP双対を使えるようにする：弱双対/強双対、相補スラックネス（complementary slackness）を通じて、最適性のチェックと感度の見方を身につける。 ロバスト最適化の入口：不確実性集合を置き、最悪ケースで制約を満たす（robust constraint）を双対性で再定式化する感覚を掴む。	Module 17–18
10	大規模最適化（列生成）：切断在庫（cutting stock）を例に、Gilmore–Gomory定式化→列生成（pricing）→反復の流れを学ぶ。 制約生成との対比：primal-dualの観点で、constraint generation / separation problem を整理する。	Module 19–20
11	分解法（Dantzig–Wolfe）：構造を exploit する、分解して master + subproblem に落とす、という設計思想を学ぶ。 近似/フィッティングの最適化：最小二乗、ノルム、正規方程式、SVDなどを最適化モデリングとして捉え直す。	Module 21–22
12	円錐計画（Conic）：凸円錐と順序、SOCP/SDPの基本を押さえ「線形→円錐」への拡張を理解する。 SOCP/SDPの典型例：分類、実験計画、最小包含楕円体などで“何が嬉しいか”を体験する。	Module 23–24
13	離散最適化の全体像：離散変数が必要になる理由、難しさ（計算量/NP-hardnessの直観）を整理する。 0-1変数で論理を表す：非凸な関係や論理関係を、バイナリ変数と制約で書く基本パターンを学ぶ。	Module 25–26
14	0-1モデリングの実戦：集合被覆/集合分割/集合詰め込み、グラフ・ネットワークなどの代表問題を「制約の型」として身につける。 演習で定式化を固める：モデリング演習で、落とし穴（抜け・重複・線形化）を潰す。	Module 27–28
15	LP緩和を理解する：離散問題をLP緩和で眺め、良い定式化（ideal formulation）の意味を学ぶ。 代表的解法：列挙、カット平面、分枝限定（branch-and-bound）、ヒューリスティクスの位置づけを整理する。	Module 29–30

受講してみた感想

一通り授業を受けて、私自身とても勉強になりました。

自分の大学でも上記のような授業を受けたことが無かったし、ズバリの授業も無かった気がしています。まあ学科によるとは思うけど。
辛かったのは計算ですね。試験が手計算なんですが、自分の計算力の衰えに愕然としました。3*3の行列の特異値分解とか計算ミスしちゃったりして。

そしてこの授業で一番お世話になったのは、梅谷先生の「しっかり学ぶ数理最適化」ですね。ほんとバイブルでした。深謝。
問題クラスとかあんまりどこにもちゃんと載って無かったんですが、めっちゃちゃんと書いてあって、あらためてカバー範囲がすげーなと思いました。

どんなことを習うのかの例

ここからは、個人的にへーってなったトピックを例に、どんなこと習うのかの例を少しだけ紹介します。
Dantzig–Wolfe分解と列生成法の関係について書くか迷ったんですが、書くのめんどくさそうだったので、ロバスト最適化の方を選びました。

ロバスト最適化：ロバスト制約を双対で有限個の制約に落とす

問題設定：不確実な係数を持つ制約

次のような最適化問題を考えます：

$$
\min \quad \mathbf{c}^T \mathbf{x}
$$

$$
\text{s.t.} \quad \mathbf{a}^T \mathbf{x} \leq b, \quad \forall \mathbf{a} : \mathbf{B}\mathbf{a} \leq \mathbf{d}
$$

ここで、制約係数 $\mathbf{a}$ が正確には分からない状況です。不確実性集合 $U$ は多面体で定義されるとします：

$$
U = {\mathbf{a} \in \mathbb{R}^n : \mathbf{B}\mathbf{a} \leq \mathbf{d}}
$$

問題点：$U$ が連続集合だと、$\mathbf{a}^T \mathbf{x} \leq b$ という制約が「$\mathbf{a}$ の候補が無限にある」ため、無限個の制約式になってしまい、そのままでは計算機で扱えません。

結論：双対で書き換えるとこうなる

最終的な定式化（LP）：

$$
\min \quad \mathbf{c}^T \mathbf{x}
$$

$$
\text{s.t.} \quad \mathbf{d}^T \mathbf{y} \leq b
$$

$$
\mathbf{B}^T \mathbf{y} = \mathbf{x}
$$

$$
\mathbf{y} \geq \mathbf{0}
$$

変数について：

• $\mathbf{x}$：元々の主問題の変数（元の問題の符号制約に従う）
• $\mathbf{y}$：双対問題から導入された補助変数（$\mathbf{y} \geq \mathbf{0}$）
• 両方とも変数として扱われ、$\mathbf{B}^T \mathbf{y} = \mathbf{x}$ という等式制約で結ばれています

変換のロジック（ステップ1,2,3）

ステップ1：最悪ケースの定式化（主問題）

「全ての $\mathbf{a}$」を相手にするのではなく、「左辺が最大になる最悪の $\mathbf{a}$（$\max \mathbf{a}^T \mathbf{x}$）でも $b$ 以下であればよい」と定式化します：

$$
\max_{\mathbf{a} : \mathbf{B}\mathbf{a} \leq \mathbf{d}} \mathbf{a}^T \mathbf{x} \leq b
$$

ステップ2：双対性による「変数同士の積」の解消

制約式 $\mathbf{a}^T \mathbf{x} \leq b$ において、$\mathbf{x}$ は決定変数であり、$\mathbf{a}$ もまた最悪ケースを探す過程で動く変数のように振る舞います。この「変数 $\times$ 変数」という双線形（二次）の項が、問題を解く上で邪魔。

そこで、内側の最大化問題を、強双対性を利用して双対問題に書き換えます。ここでのポイントは、「$\mathbf{x}$ を定数とみなして」双対を取ることです。

$$
\text{(P)}: \quad \max_{\mathbf{a}} \quad \mathbf{x}^T \mathbf{a}
$$

$$
\text{s.t.} \quad \mathbf{B}\mathbf{a} \leq \mathbf{d}
$$

$$
\text{(D)}: \quad \min_{\mathbf{y}} \quad \mathbf{d}^T \mathbf{y}
$$

$$
\text{s.t.} \quad \mathbf{B}^T \mathbf{y} = \mathbf{x}
$$

$$
\mathbf{y} \geq \mathbf{0}
$$

双対変換を経ることで、目的関数にあった変数同士の積 $\mathbf{x}^T \mathbf{a}$ が消え、変数 $\mathbf{x}$ は線形な等式制約（$\mathbf{B}^T \mathbf{y} = \mathbf{x}$）の中に分離されました。これにより、扱いにくい二次の関係が、扱いやすい一次（線形）の関係へと解体されます。

ステップ3：決定論的制約への書き換え（統合）

「（双対問題の）最小値 $\leq b$」であればよい。これは最小値を厳密に求めなくても、「条件を満たす $\mathbf{y}$ が存在し、その時の値が $b$ 以下（$\mathbf{d}^T \mathbf{y} \leq b$）」であれば達成できます。これにより、「最適化問題」の枠が外れ、単なる連立不等式（Afterの形）だけが残ります：

$$
\max_{\mathbf{a} : \mathbf{B}\mathbf{a} \leq \mathbf{d}} \mathbf{a}^T \mathbf{x} \leq b
$$

$$
\Longleftrightarrow \exists \mathbf{y} \geq \mathbf{0} \text{ s.t. } \mathbf{B}^T \mathbf{y} = \mathbf{x}
$$

$$
\mathbf{d}^T \mathbf{y} \leq b
$$

結果：ロバスト制約（無限個）が、普通の線形制約（有限個）に落とせた！

定式化お役立ち

リンク集

最後にお役立ちリンク集です。こんな感じの定式化tipsがまとまってます↓(ref: Laurent Lessard)

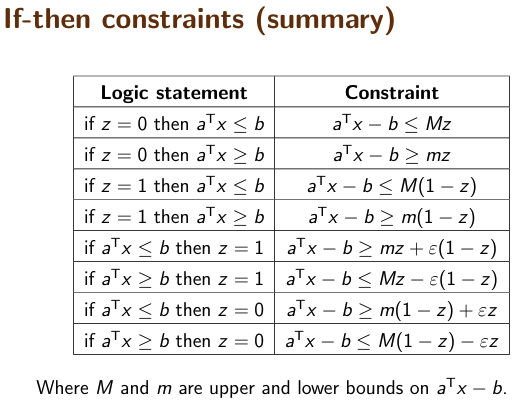
この辺は実務で日々使っているから楽勝だろうと思ってたんですが、こうやって網羅的にひたすら練習問題を解いてみると、「あれ、なんでこう書いたらダメなんだっけ」、「同じこと言ってるけどこっちの方がエレガントだな」みたいな気づきが沢山得られました。

良く定式化はセンスと言われます。実際、未知の問題を解く時は、こんな教科書通りの問題はあり得ないです。でも、センスとは筋の良い定石を学んで養っていくことが大事だと思います。(と、将棋の先生に教わりました)

1. Logic constraints and integer variables (Lessard)
   「論理制約を整数変数でどう表現するか」を、スライド形式で視覚的に分かりやすくまとめた資料です。

2. Linear Programming Formulation
   線形計画法における定式化の基礎から、絶対値や区分線形関数の扱いといった実践的なテクニックを網羅しています。演習問題を通じて、数式化のコツを体系的に学べます。

3. Either-or & if-then constraint formulation
   「AまたはB」や「もしAならB」という論理条件を数式にする方法を解説した動画です。

4. Integer Programming Tricks
   整数計画法における定式化のコツを、数学的に厳密かつ整理された形でまとめた秘伝のタレ的な資料です。

5. MIT's cutesy talking animals
   良くわかんない動物たちが会話するストーリー形式で、複雑な論理モデル化を学べるMITのチュートリアルです。

6. Truth Tables and Logic
   定式化の土台となる「真理値表」や「論理的同値」を基礎から復習できるサイトです。