テキスト「Pythonで学ぶ債券·金利デリバティブ」の78ページや101ページで説明を避けた「ブートストラップ時の連立方程式の解法」が今回のメインテーマ。
第3回で予告したHagan-West流の多変数ニュートン法でブートストラップを計算することが実務で標準的に用いられる計算法。
- この回では第3回の2節のカーブオブジェクトが算出した3つのディスカウントファクター(以下 DF)をHagan and Westが2008年に発表した論文 "Methods for Constructing a Yield Curve"に沿って、手計算を例示する
- 上記論文の第2章
Interpolation And Bootstrap Of Yield Curves—Not Two Separate Processesに記載されたブートストラップ計算法をここでは、Hagan-West流の計算法と参照し、そのアルゴリズムを次の5ステップに分けて説明する- guess → interpolate → pricing → update → fixed point
1. 3商品のディスカウントファクター 算出コード
- まず 3商品
(6mTibor, 1x7FRA, 2ySwap)から3つのDF を同時に計算する次のコード(以下"61行コード"と参照)を実行し、四角で囲った最後の2行の値と第3回の2節で算出したDFとを比較しよう

- 第3回で断念した2年スワップ満期日(2027-12-23)のDF=0.9718779323 が算出できている
- 更に6mTibor(2026-06-23)と1x7FRA(2026-07-23)も同時に計算され、前回と同じ値
- 各コードの意味は随時 説明するが、大まかな内容はA~Dで始まるコメントから推測しよう
- この"61行コード"はHagan-West流の以下のアルゴリズムを再現したもの
-
guess:19行目で初期値
iRT=0.001を設定(iRTはinitial rateの略) -
interpolate:6行目
DiscountCurveコンストラクタによって、カーブがguessの値で作られ、7,8行目は補間されたディスカウントファクターを算出 - pricing:11~13行目では、作成されたカーブで3商品のレートを計算し、市場レートとの差を算出
- update:41~53行目は市場レートとの差を小さくするため、ニュートン法が実行され、カーブを微調整させるループ
- fixed point:調整されたカーブによる3商品のレートが市場レートと一致し、43, 44行目でニュートン法のループが終了。 59, 60行目でそのカーブのディスカウントファクターを出力
-
guess:19行目で初期値
2. ニュートン法 入門 (別名: Newton–Raphson法)
まずはニュートン法を紹介する。
-
ファイナンスの計算において、複利利回りやインプライドボラティリティーの算出にはニュートン法がよく利用される。ただ ニュートン法は微分計算$f'(x)$が必要となり、コードが長くなる
- 第2回記事の3節 JGBクラスのコード説明では、微分を避けるために、
Brent法で日本式複利を実装した(多次元のBrent法は無い)
- 第2回記事の3節 JGBクラスのコード説明では、微分を避けるために、
-
この回ではニュートン法を避けて通れない。実はニュートン法には次の2種類がある
-
方程式 $\mathbf{f(x) = 0}$ の解 $\mathbf{x^*}$ を求めるタイプ
- この
root-findingのニュートン法のテイラー展開は1次で十分
- この
-
最小化問題 $\mathbf{\min_x f(x)}$ を解くタイプ
- テイラー展開が2次まで必要
(Hessianの計算)
- テイラー展開が2次まで必要
-
方程式 $\mathbf{f(x) = 0}$ の解 $\mathbf{x^*}$ を求めるタイプ
-
ここでは
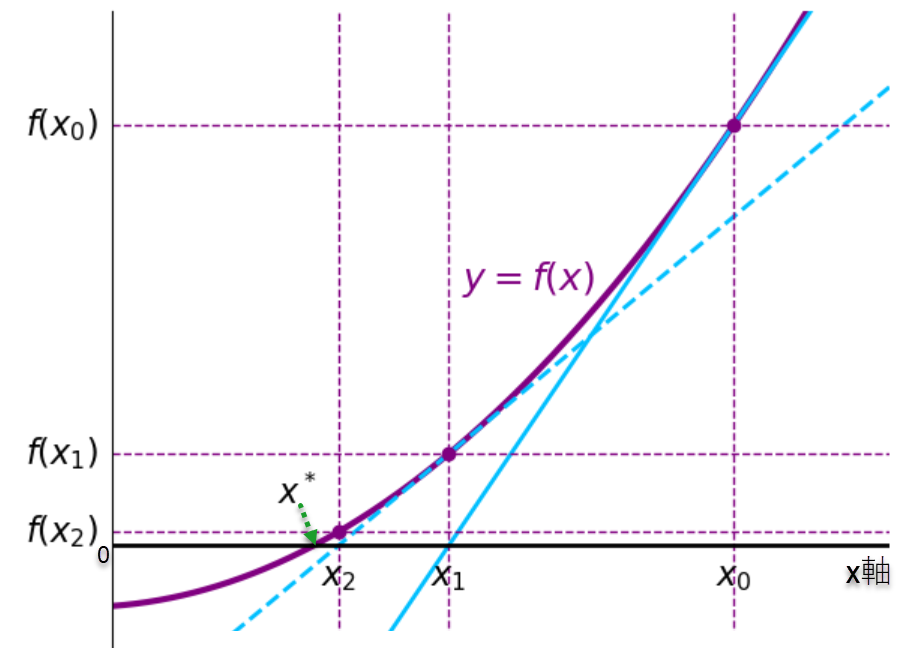
f(x)=0の解のニュートン法となり、初めに1変数の場合をイメージ的に説明する- 下図において、$f(x) = 0$の解は$f(x)$とx軸の交わる点で $\mathbf{x^*}$ と参照する
- 初期値を $\mathbf{x_0}$ とすると、$f(x_0) \neq 0$であり $x_0$は$f(x)$の解ではない
- 点 $x_0$ でテイラー展開し、
$$f(x) \approx f(x_0) + f'(x_0)(x - x_0) \tag{S1}$$0 = 右辺と置き、
$$0 = f(x_0) + f'(x_0)(x - x_0) \tag{S2}$$ $x$について解いた解を$\mathbf{x_1}$とする
$$x_1:= x_0 - \displaystyle{\frac{f(x_0)}{f'(x_0)}}$$ (ここで確認すべき点) - 2回目の計算として、初期値$x_0$を$x_1$で置き換え、同じ計算を行えば、図の$\mathbf{x_2}$を得る
- ニュートン法はこの計算をn回 繰り返し、$x^*$に十分近づいた値$\mathbf{x_{n}}$を解とする
- 上図では、2回目の計算の解である $x_2$ が 既に $x^*$ に近づいている
- "61行コード"では 出力欄の
#3 fx=[ 0. -0. 0.] diff=2.34e-16が示すように、3回のループで解を見つけている
- 一般化すると$$x_{n+1}= x_{n} - \displaystyle{\frac{f(x_{n})}{f'(x_{n})}}$$
- 右辺の2項目をニュートンステップと呼び、次式で表す
$$\Delta x_{n} := - \displaystyle{\frac{f(x_{n})}{f'(x_{n})} = -f'(x_{n})^{-1}\ f(x_{n}) \tag{S3}}$$ - ニュートン法はニュートンステップを用いて、次式でコーディングする
$$x_{n+1}= x_{n} + \Delta x_{n} \tag{S4}$$ -
コード53行目は レート用変数yldをニュートンステップdyで更新するコードyld = yld + dy-
yldは37行目で、( 初期値レート 0.1% x 3商品の年数[yr6m, yr7m, yr2y] )で計算した年限に応じたレートの配列 (要素数は3で、符号はマイナスへ) - Hagan-West流では
yldが初期値となり、式$(S1)$の $x_0$に相当
-
- ニュートンステップ
dyは40~53行目のforループにより更新し、43行目 if diff < tol:で解に近づいたかを判定(tolは19行目で設定)
- 右辺の2項目をニュートンステップと呼び、次式で表す
-
(1変数ニュートン法 まとめ) 現在の近似値 $x_n$ のまわりで、関数 $f(x)$ を一次近似(接線)し、その接線が$x$軸と交わる点を次の近似値にする
(1) 点 $x_n$ でテイラー展開:$\quad\quad f(x) \approx f(x_n) + f'(x_n)(x - x_n)$ $\ (S1)$
(2) 近似した関数 = 0を解く:$\quad\quad\ \ \ 0 = f(x_n) + f'(x_n)(x - x_n) \quad$ $(S2)$
(3) ニュートンステップ:$\qquad\quad \Delta x_{n} = -f'(x_{n})^{-1}\ f(x_{n}) \qquad\qquad\ (S3)$
(4) 次の反復点:$\quad\quad\quad\quad\quad\quad \ x_{n+1} =x_{n} + \Delta x_{n} \quad \quad\quad\quad\quad\ \ \ $ $(S4)$
3. コード詳細 と 3変数のニュートン法
では "61行コード"を1行目から順に読んで行く。1行目はいつものように2つのモジュールを読み込んでいる。(2つのモジュールはテキスト1.4節 参照)
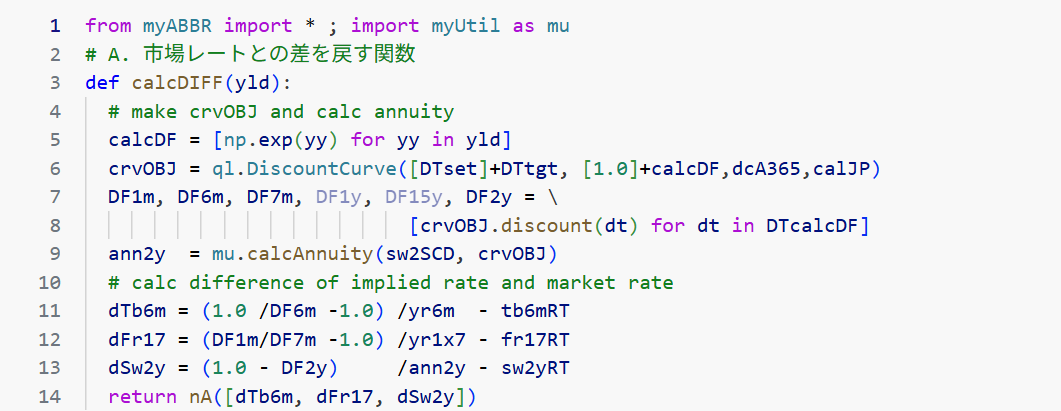
# A. (市場レートとの差を計算する関数)
3行目で式$(S1)$の $f(x)$ に相当する関数として、calcDIFF( yld ) 関数を定義
- 関数の引数 yld について
-
41行目でこの関数が初めて呼び出される - 引数
yldの初期値は37行目で、-0.1% x [yr6m(0.5年), yr7m(0.58年), yr2y(2年)]と計算した[-0.0005, -0.00058, -0.002]("レート x 年限"にマイナスを掛けた値)- マイナスの理由は
5行目で[np.exp(yy) for yy in yld]のように、引数yldから各年数のディスカウントファクターを計算するため - このディスカウントファクターから、6行目でカーブオブジェクトを作成
- マイナスの理由は
- この引数 yld を
レート x 年限という変数にした点が重要- Hagan and Westの2006年の論文 "Interpolation Methods for Curve Construction" では、「レートを直接いじるのではなく、無裁定性を(構造として)満たしやすい変数を選ぶ」という趣旨を記述
-
-
6行目DiscountCurveコンストラクタ:ディスカウントファクターからイールドカーブを作るコンストラクタで、左辺のcrvOBJオブジェクトを作成(テキストでは扱っていない初登場のコンストラクタ)- 引数は DiscountCurve(
dates, DFs, dayCounter, calendar) - 対応するC++クラスはInterpolatedDiscountCurve < LogLinear > Class
- このクラス詳細は
テキスト1.6節で説明したQuantLibリファレンスマニュアルを参照
- このクラス詳細は
- 引数は DiscountCurve(
-
7~13行:3商品(6mTibor, 1x7FRA, 2ySwap)の各レートをディスカウントファクターから計算-
7,8行:計算に必要なディスカウントファクターをdiscountメソッドで取得 -
9行:mu.calcAnnuity関数で2ySwapのアニュイティを計算(calcAnnuity関数はテキスト 69ページ 2.8.2節参照) -
11~13行:右辺第1項で6mTibor, 1x7FRA, 2ySwapの各レートを計算し、それぞれの市場レートとの差を変数dTb6m, dFr17, dSw2yへ設定し、関数の戻り値を準備(dはdifferenceの略)- この各レートの計算を QuantLib C++ではヘルパーオブジェクトが行うため、手計算は不要。しかし、QuantLib-Pythonのヘルパーにはその機能が無いため、手計算した
-
- この関数の3つの戻り値がすべてゼロとなるDiscountCurveコンストラクタの引数 DFsを探し出すことが目的
- 補足すると、5行目の
[np.exp(yy) for yy in yld]で DFs は yld から計算される。つまり、関数の戻り値がゼロとなるyldをニュートン法で見つける作業となる
- 補足すると、5行目の
- 確認のために記すが、calcDIFF関数を$\mathbf{f}$とすると、この関数は引数が3つ、戻り値も3つで、3変数のニュートン法の計算が必要
$$
f:\mathbb{R}^3 \to \mathbb{R}^3,\qquad
f(x,y,z)
=\begin{pmatrix}
f_1(x,y,z)\\
f_2(x,y,z)\\
f_3(x,y,z)
\end{pmatrix}
$$-
その際 1変数のニュートン法の微分 $f'(x)$はヤコビ行列
(Jacobian matrix または 単にヤコビアン)となる- ヤコビ行列とは多変数関数の偏微分を並べた行列で、役割は1変数関数の微分 $f'(x)$ と変わらない
- (簡単な例) 次の2変数関数の場合 $$
\begin{cases}
f_1(x,y) = x^2 + y \\
f_2(x,y) = xy
\end{cases} $$ ヤコビ行列は $$
J(x,y) =
\begin{pmatrix}
\dfrac{\partial f_1}{\partial x} & \dfrac{\partial f_1}{\partial y} \\
\dfrac{\partial f_2}{\partial x} & \dfrac{\partial f_2}{\partial y} \\
\end{pmatrix}
=\begin{pmatrix}
2x & 1 \\
y & x
\end{pmatrix}
$$
-
(3変数のヤコビアンは下の
#C節に記載)
-
# B. (日付, 市場レート等の初期値設定)
17~34行は各初期値の設定と3商品のレート(11~13行目 右辺 第1項)を算出する際に必要となる日付/年数の準備
-
#A節で記したように、3商品のレートの計算を QuantLib C++ではヘルパーオブジェクトが行うので、この#B節もC++を使った場合、ほぼ不要- 似たような記号で変数を定義したが、Hagan-West流の本道ではないので、理解しなくても大丈夫
- 目的の「ディスカウントファクターから3商品をpricingすること」を忘れないように!
一応、変数の意味を説明する。
-
19, 20行 eps,tol,maxIter= 1e-7,1e-14,30:eps, tol, maxIter はそれぞれ 有限差分幅(bumpの大きさ), 収束判定, 最大反復回数を表し、49行目, 43行目, 40行目 で使われる- これらの値の設定はQuantLib C++コードを参考にした
-
23, 27行:2ySwapのスケジュールを設定し(テキスト 49ページ 2.3.2節参照)、27行目で各日付をそれぞれの変数に代入- 変数への代入は本来不要。ただコードを判りやすくするための処置
-
25, 28行:1x7FRAのスケジュールを設定し、日付用の変数を設定 -
29行 DTtgt:求めたい3商品のディスカウントファクターの日付リスト(tgtはtargetの略) - `30行:3商品のレートを算出する際に必要となるDFの日付リスト
-
31~34行:各日付をdcA365ベースで年数に変換(dcA365はテキスト 8ページ 参照)
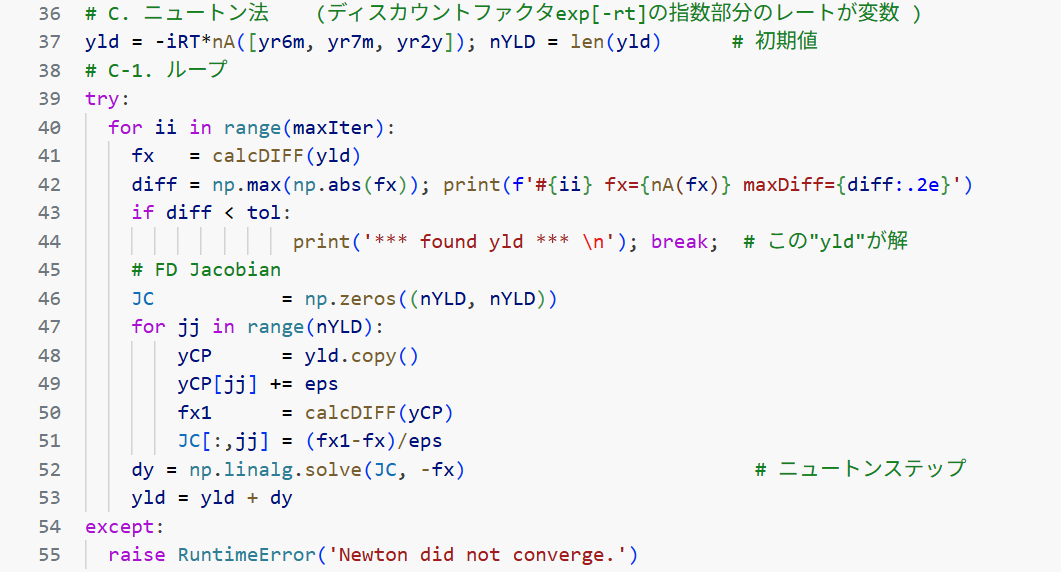
# C. (ニュートン法)
37~44行までは大半が説明済みであるが、多少補足する
-
41行:calcDIFF関数に37行目で計算された初期値 yld を与えて、戻された値を変数fxに設定- この
fxはニュートン法の$f(x_0)$に対応
- この
-
42, 43行:42行目のプリント文からの出力#0 fx=[-0.00971 -0.01015 -0.0133 ] diff=1.33e-02が$f(x_0)$の内容で、市場レートとの最大の差は diff=1.33e-02- 初期値 0.1%のレート
(19行目 iRT=0.001)で算出されたディスカウントファクターで3商品が評価されているため、この値では43行目の判定はFalseとなり、45行目に処理が移る
- 初期値 0.1%のレート
-
45, 46行:コメント行のFD Jacobianは有限差分でのヤコビアン(finite difference Jacobian)を意味し、46行目でJC(ヤコビアン)という3行3列のゼロ行列を作成 -
以下は1変数のニュートン法の表記を3変数に対応させた数式
(式番号はSxxとMxxが対応)-
(1) 3商品を$x, y, z$ とし、$f$をベクトル関数をすると、
$$f:\mathbb{R}^3\to\mathbb{R}^3,\quad f(x,y,z)=
\begin{pmatrix}f_1(x,y,z)\\ f_2(x,y,z)\\ f_3(x,y,z)\end{pmatrix}$$- 右辺の$f_1(x,y,z)$が
14行目のdTB6m、$f_2(..)$がdFr17、$f_3(..)$がdSw2yを意味 - 近似値 $ \boldsymbol{x}_n = \begin{pmatrix} x_n, \ y_n, \ z_n \end{pmatrix}$で1次テイラー展開は
$$\boldsymbol{f}(\boldsymbol{x}) \approx \boldsymbol{f}(\boldsymbol{x}_n) + J(\boldsymbol{x}_n)\ (\boldsymbol{x}-\boldsymbol{x}_n) \tag{M1}$$ - $J(\boldsymbol{x})$はヤコビアン
(ヤコビ行列、Jacobian matrix)
$$
J(\boldsymbol{x})
:= \frac{\partial (f_1,f_2,f_3)}{\partial (x,y,z)}=
\begin{pmatrix}
\frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} & \frac{\partial f_1}{\partial z} \\
\frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} & \frac{\partial f_2}{\partial z} \\
\frac{\partial f_3}{\partial x} & \frac{\partial f_3}{\partial y} & \frac{\partial f_3}{\partial z}
\end{pmatrix}_{(x_n,\ y_n,\ z_n)}
\tag{$f'(x)$相当}$$- 最後の添字 $(x_n,\ y_n,\ z_n)$ は「この点で評価する」という意味(文脈で明らかなら省略)
- 右辺の$f_1(x,y,z)$が
-
(2) 近似式を $\boldsymbol{x}$ について解く
$$ \boldsymbol{0} = \boldsymbol{f}(\boldsymbol{x}_n) + J(\boldsymbol{x}_n) (\boldsymbol{x} -\boldsymbol{x}_n) \tag{M2}$$ - (3) ニュートンステップは $$ \Delta\boldsymbol{x}_n := - J(\boldsymbol{x}_n)^{-1}\ \boldsymbol{f}(\boldsymbol{x}_n) \tag{M3}$$と表せ、次式でコーディングする
$$ \boldsymbol{x}_{n+1} = \boldsymbol{x}_n + \Delta\boldsymbol{x}_n \tag{M4}$$
-
(1) 3商品を$x, y, z$ とし、$f$をベクトル関数をすると、
-
では再度 "61行コード"に戻ろう
-
47~51行 for jj in range(nYLD):このforループで、有限差分によるヤコビアンを作成 -
48行 yCP=yld.copy():いわゆる値渡しにするため、.copyを付けている- Pythonリスト / numpy配列は参照渡し、Pythonタプルは値渡し
- もし
yCP = yldだけだと"参照渡し"となり、49行目のyCP[jj] += epsはオリジナルのyldの値も変化させてしまう - Pythonに"値渡し/参照渡し"の概念はなく、上は比喩的な説明
- (オブジェクト生成後に中身を変更できる場合をmutableといい、mutableオブジェクトは参照渡しのように振る舞う)
-
49, 50行 yCP[jj] +=eps:yCPの $jj$ 成分だけを微小量 $\varepsilon$(epsは19行目で定義)変化させ、calcDIFF関数を呼び出して、$fx1$を作成 -
51行 JC[:,jj]=(fx1-fx)/eps:右辺を有限差分で計算し、ヤコビアンの$jj$列を更新- スライス
JC[:,jj]のコロン :は "すべての行" を意味 - 例えば、$jj=0$では第1列の$x$の偏微分の列が更新される
$$
\begin{pmatrix}
\frac{\partial f_1}{\partial x} & \frac{\partial f_1}{\partial y} & \frac{\partial f_1}{\partial z} \\
\frac{\partial f_2}{\partial x} & \frac{\partial f_2}{\partial y} & \frac{\partial f_2}{\partial z} \\
\frac{\partial f_3}{\partial x} & \frac{\partial f_3}{\partial y} & \frac{\partial f_3}{\partial z}
\end{pmatrix}
$$ - 47行目のforループで、第2列の$y$の偏微分の列、第3列の$z$の偏微分の列が計算され、ヤコビアン全体を更新
- (些細な点であるが、Hagan-West"法"という場合、この計算は有限差分ではなく、偏微分した式が必要)
- スライス
-
52行 dy=np.linalg.solve(JC, -fx): このコードは "61行コード"の中で最も重要で、1行~51行までの計算が集約され、ニュートンステップ$dy$を計算(linalgは linear algebraの略)-
式$(M3)$を書き直せば、次式$(M3')$ $$ J(\boldsymbol{x}_n) \Delta\boldsymbol{x}_n = -\boldsymbol{f}(\boldsymbol{x}_n) \tag{M3'}$$
- (ヤコビアンが判りにくければ、微分の式$(S3)$で考えよう)$$f'(x_{n})\ \Delta x_{n}=-f(x_{n}) \tag{S3'}$$
-
式$(M3')$と52行目コード
dy=np.linalg.solve(JC, -fx)の対応関係-
solveメソッドの第1引数JCは51行目で計算されたヤコビ行列$J(\boldsymbol{x}_n)$ - 第2引数
-fxは41行目のcalcDIFF関数の戻り値をマイナスにしたもの - 式$(M3')$のニュートンステップ$\Delta\boldsymbol{x}_n$は52行目で計算される左辺の$dy$
-
-
-
次の連立方程式を解く行列演算のコードを理解し、式$(M3')$の行列演算と比較しよう
$$
\begin{cases}
2x + y = 1 \\
x + 3y = 5
\end{cases}
$$- この連立方程式を行列で表現すれば、
$$
A =
\begin{pmatrix}
2 & 1 \\
1 & 3
\end{pmatrix},
\quad
b =
\begin{pmatrix}
1 \\
5
\end{pmatrix}
と置き,\quad
A \begin{pmatrix}
x \\
y
\end{pmatrix}
= b
\tag{M5}
$$ - この解をlinalg.solveで計算するコードは、行列$A, b$を使い、以下となる

- 4行目で
np.linalg.solve(A,b)と記入し、解$x$を得る- 逆行列を作る必要はない
(補足) 5行目の @ は行列の掛け算
- 逆行列を作る必要はない
- 式$(M3')$と$(M5)$を比較すれば、
52行目は理解できるだろう
- この連立方程式を行列で表現すれば、
-
D. (見つかった解 "yld" でDFを算出)
-
58, 59行目は5, 6行目のコピーであり、説明は省略- ただし、58行目の
yldは42, 43行目から飛んできた見つかった解 yldである
- ただし、58行目の
-
59行目 nSetF(10) ... nSetF(): myABBRモジュールで定義したnumpy配列の桁数を指定する短縮形(テキスト 322ページ 参照)-
nSetF(10)により、DFの出力を少数10桁表示に設定 - 後半の
nSetF()は初期設定である少数5桁表示に戻した
-
まとめ
- Hagan-West流の計算法によるブートストラップはQuantLibや金融業界で標準的に使用される
- 著者のテキストに、この計算法を一言も記述していないが、その理由は多変数ニュートン法が登場し、かなり難解なため
- この記事から覚えておくべきことは「イールドカーブのノードを構成する商品を正しく評価するディスカウントファクターをニュートン法で見つけていること」くらいで十分
(冒頭に説明した"5ステップのアルゴリズム"でもよい) - QuantLibを使えば、簡単にこの計算法によるディスカウントファクターを得られるので、その他の面倒な部分は忘れても構わない
- 上記コードはテキストのサポートページ より、取得可能
(ファイル名:HaganWestCalcDF.ipynb, myABBR.py)