テキスト「Pythonで学ぶ債券·金利デリバティブ」第2章で説明したTiborカーブでは意図的にシリアルFRA(Forward Rate Agreement)を取り除いた。その理由はシリアルFRAという用語が一般的ではないため。
- シリアルFRAとはFRAの中で最も基本的な商品
- 広い意味のシリアルFRAはテナーがTiborと同一(例えば3ヶ月)で、開始月が連続のFRA
- FRAは「開始月 x 終了月」で表され、
1x4, 2x5, 3x6等がシリアルFRA
- FRAは「開始月 x 終了月」で表され、
- 狭義のシリアルFRAは開始月と終了月がテナー刻みで連続なFRA
例:3x6, 6x9, 9x12
ただ テキスト第3章のTONAカーブ構築で説明したフォワードレートによるディスカウントファクター算出の次式(テキスト78ページ 式3.1)はFRAの計算法そのもの。
$$
\begin{split}
D_E
&=
D_S \times \left(
\frac{1}{1+ f_{S \times E}\times \tau}\right)\ , \quad \tau : E-S
\end{split}
\tag{3.1}
$$
そこで、今回は以下の各項目を説明する
- 日本証券クリアリング機構 (以下 JSCC) はTONAカーブとのベーシススプレッドとしてTiborカーブを公表しているが、その算出法
- シリアルFRAをいれたTiborカーブ構築のコード例と手計算による確認
-
テキスト 78ページや101ページで説明を避けた「ブートストラップ時の連立方程式の解法」部分の実務で用いられている計算法 (Hagan-West法)
1. JSCCのFixingレート
-
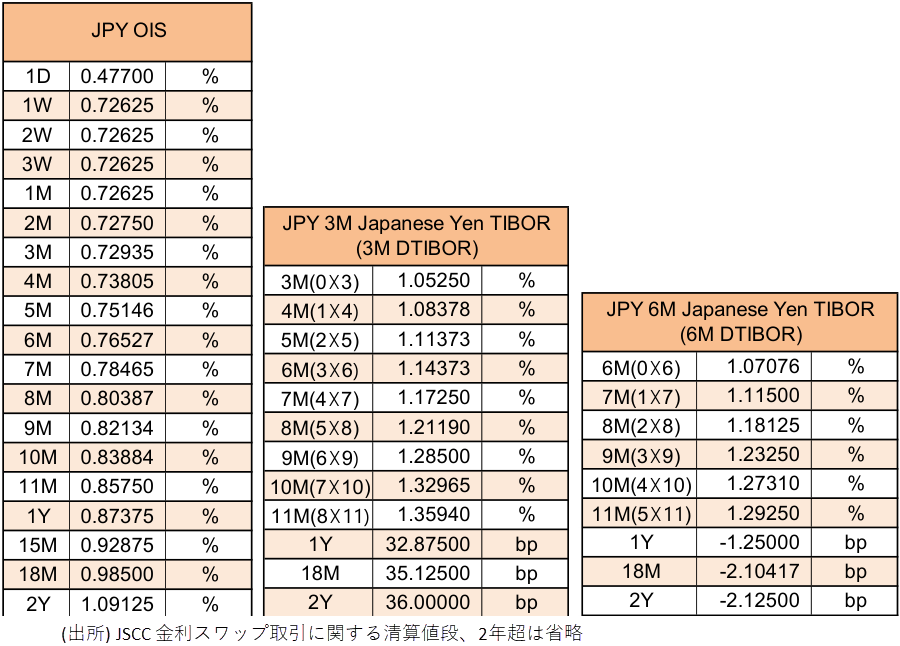
下図はJSCCが発表した2025年12月19日引けのFixingデータ
-
各種レートの意味とTiborスワップレートの計算
- OISは%単位のレート (ディスカウントカーブの役割)
- DTIBORの
Dはdomesticの略で、今は無いユーロ円Tiborと区別する記号。この記事ではDは省略 - 3ヶ月Tiborカーブ(以下
3図mTiborカーブ)は8 x 11までは3ヶ月テナーのシリアルFRAのレート、1年以上はOISとのベーシススプレッド (フォワードカーブの役割)- 2年スワップレート:
1.09125%+36.0bp = 1.45125%
- 2年スワップレート:
- 6ヶ月Tiborカーブは5 x 11までは6ヶ月テナーのシリアルFRAのレート、1年以上は3mDTiborカーブとのテナーベーシススプレッド (フォワードカーブの役割)
- 2年スワップレート:
1.09125%+36.0bp-2.125bp = 1.4300%
- 2年スワップレート:
2. FRAのヘルパーと実行例
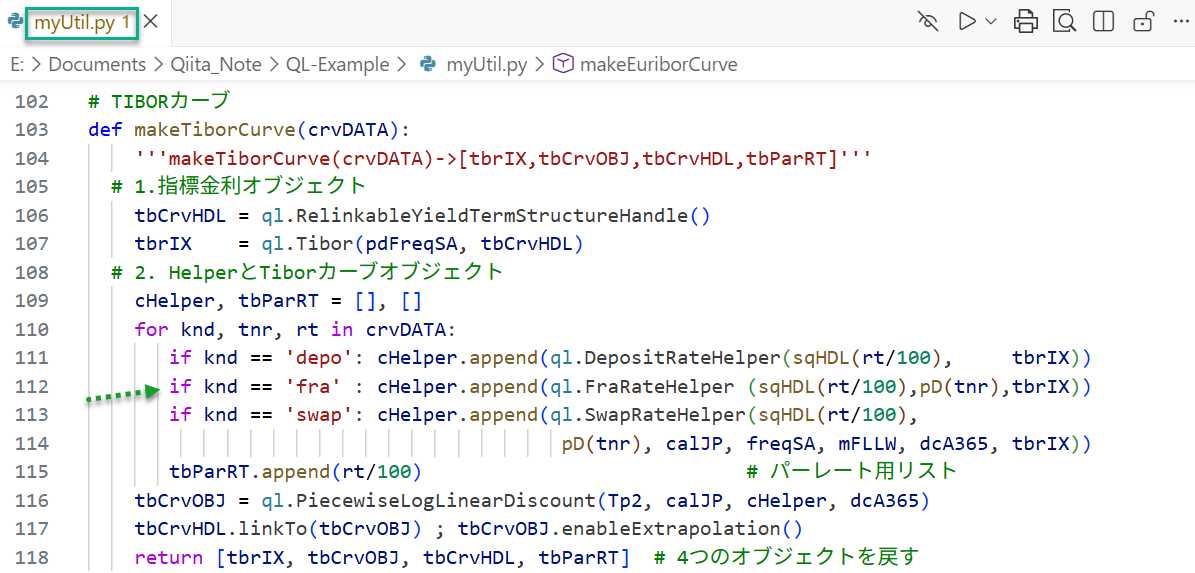
$\qquad\qquad\qquad\qquad\qquad\qquad$(図3-1)
-
上図はテキスト2.2.4節で説明した
myUtil.pyモジュールのTIBORカーブ作成関数makeTiborCurveにFRA用のヘルパーを追加したコード- 修正点は矢印の行のみで
FraRateHelperコンストラクタを追加 - すぐ上の行の
DepositRateHelperと比べて、FRAの開始月を表す引数pD(tnr)が1つ増えただけ - シリアルFRAの知識があれば、簡単なコンストラクタである
- 修正点は矢印の行のみで
-
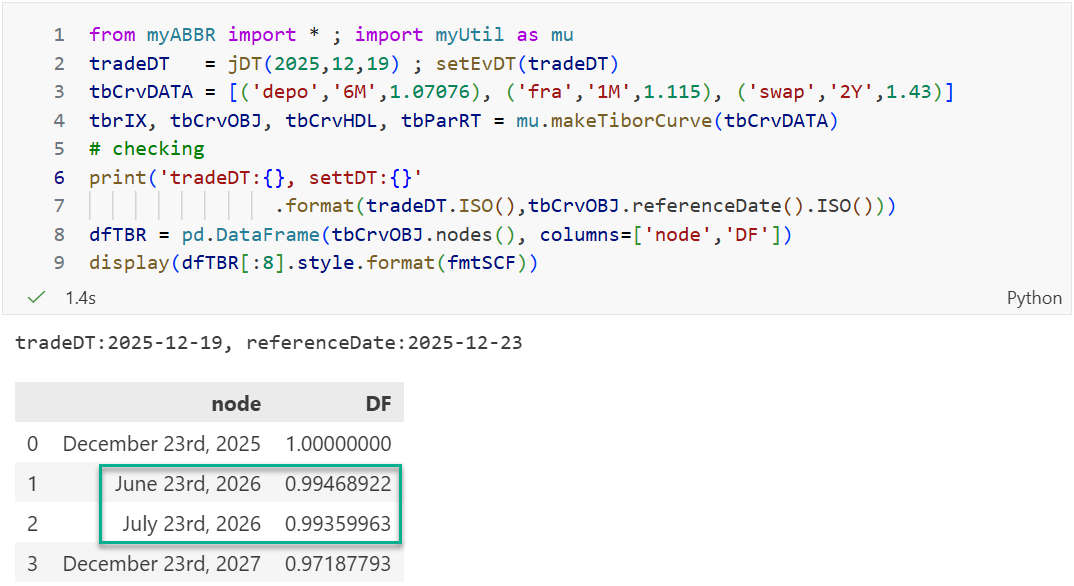
下図はJSCCのデータをこの
mu.makeTiborCurveに与えて、ディスカウントファクターDFを算出した例(テキスト図2.3とほぼ同じコード) -
次の下2つのセルは6mTiborと1x7 FRAのディスカウントファクターを手計算した例
-
ただし、FRAの計算はテキスト78ページの説明と同様、1ヶ月先のDFを5行目
tbCrvOBJ.discount(DT1m)で取得する”手抜き”の計算 -
確認すべきは、FRAから計算されるDFはFRAの満期日のDFである点
- (筆者は10数年前に初めてシリアルFRAを見た。当時 FRAのDFをフォワードのディスカウントファクターと誤解した経験があり、まだ苦手意識が残っている)
3. 2年ディスカウントファクターの連立方程式
-
2年ディスカウントファクターはブートストラップ
(定義はテキスト97ページ)で算出 -
2年スワップの満期日(2027年12月23日)のディスカウントファクターは
テキスト 101ページ (Semiannualのケース)とほぼ同じ -
3つの未知数$(D_{1.0}\ D_{1.5}\ D_{2.0}\ )$を計算するための3本の連立方程式は以下となる
- テキストとの相違は7カ月のノードにFRAを入れたため、補間式では0.5年を7mに修正
$$
\begin{split}
D_{2.0} \times (1 + \tau_{2.0} S)
&= 1 - S \times \bigl( \tau_{0.5} D_{0.5} + \tau_{1.0} D_{1.0} + \tau_{1.5} D_{1.5} \bigr)
\\
\ln(D_{1.0}) &= \bigl[ \ln(D_{2.0}) - \ln(D_{7m}) \bigr] \times \frac{\text{7m〜1yの日数}} {\text{7m〜2yの日数}} + \ln(D_{7m})
\\
\ln(D_{1.5}) &= \bigl[ \ln(D_{2.0}) - \ln(D_{7m}) \bigr] \times \frac{\text{7m〜1.5yの日数}} {\text{7m〜2yの日数}} + \ln(D_{7m})
\end{split}
$$ - たった2年のディスカウントファクターを求めるのに、3本の連立方程式を解くことは苦痛
- 例えば、JSCCの発表する6ヶ月Tiborスワップでは15年の次のノードは20年
- つまり、20年のディスカウントファクターの計算の場合、未知数は10個 $(D_{15.5}$ ~ $D_{20})$となり、10本の連立方程式は見たくない
- テキストとの相違は7カ月のノードにFRAを入れたため、補間式では0.5年を7mに修正
-
(補足) 次の4節で紹介するHagan West(2006)の論文では、上で行ったディスカウントファクターの対数線形補間をRaw Interpolationと参照
(テキスト 23ページ 1.3.7節参照)
4. Hagan-West流の計算法
- この苦痛を伴うブートストラップに対し、多変数のニュートン法を用い、非線形連立方程式を解くことで、カーブ構築を行うことが現在の標準的な計算法
- この背景には 次の論文で紹介されたHagan-West法が起因する
- (2006) Interpolation Methods for Curve Construction, Applied Mathematical Finance
- (2008) Methods for Constructing a Yield Curve, WILMOTT magazine
- QuantLib C++では各種補間ルールをクラス別に実装し、上記論文で紹介されたMonotone Convex補間クラスも
InterpolatedDiscountCurveクラスから利用可能-
よく利用されるpiecewise cubic補間
通常の三次スプラインは"滑らかさ"を最優先した数学的補間法 -
monotone convex補間は"無裁定・単調性・凸性を壊さない"ことを目的した金融専用の補間法
- Hagan–West (2006) が補間したいのは "割引関数 $P(0,T)$" または "瞬間的フォーワードレート $f(0,T) = -\frac{d}{dT}\log P(0,T)$"
- この補間の際、維持すべき性質:
- 単調性: $P(0,T) \text{ は } T \text{ に対して単調減少}$
- 正のフォワードレート: $f(0,T) \ge 0$
- 無裁定性:forwardレートが局所的に暴れない
-
monotone convex補間とは、「フォワードレートを区間ごとに二次関数で表し、その積分として ディスカウントファクターを作る。その際 単調性(monotone)と凸性(convex)を強制的に守る」補間法
-
- PythonからInterpolatedDiscountCurveクラスへのアクセスは限定的ながら
DiscountCurveクラスから可能で、第4回記事の主役となる
ディスカウントファクターの計算は地味で、出来れば、避けて通りたいのが本音。しかし、Hagan-West流の多変数ニュートン法によるブートストラップを判りやすく記述した教科書(日本語、英語を問わず)が無い。
次回は上記 2年のディスカウントファクター算出を数値例とするHagan-West流の計算法を説明する。(訂正:Hagan-West法と呼ぶ場合、Monotone Convex補間を指すが、次回投稿ではこの補間法に触れないため、「Hagan-West流の計算法」に修正)
まとめ
- JSCCのベーシススプレッドを用いたTiborスワップレートの算出法
- FRAヘルパーを
mu.makeTiborCurveへ追加し、シリアルFRAのDFを算出 - FRAから計算されるディスカウントファクターはFRAの満期日のDFである
- ブートストラップ時の連立方程式の数
- Hagan-West流の計算法(
QuantLibのDiscountCurveクラス)の予告 - 上記コードはテキストのサポートページ より、取得可能
(ファイル名:q03-FRAcalc.ipynb, myUTIL.py)