(今後2,3回の投稿でQuantLibを使った物価連動国債の分析例を紹介する)
今回は通常国債の名目利回りと物価連動国債の実質利回りの差であるBreak-even Inflation(以下BEI)の計算法を説明する。
1. BEIの定義
この利回りの差であるBEIの別の表現は「通常国債と物価連動国債(以下 物国 )の投資利回りが等しくなるような 将来のインフレ率 」で、直感的には市場が織り込んだ期待インフレ率 である
-
BEIの理想的な計算はゼロレート$z$ 、同一満期 $T$ の債券に対し、
- 名目利回り $z_n(T)$ 、実質利回り $z_r(T)$ とすると、次式で算出する
$$
\text{BEI}(T) = z_n(T) - z_r(T)
$$ - ただ、この定義ではゼロレートの算出に補間やブートストラップが必要
- 名目利回り $z_n(T)$ 、実質利回り $z_r(T)$ とすると、次式で算出する
-
実務的にはゼロレートを債券満期までの複利利回り $YTM$ で置換えた次式が使われる
$$
\text{BEI}(T) =\text{YTM}_n(T) - \text{YTM}_r(T)
\tag{5-1}
$$ -
注意点として、BEI と期待インフレ率は異なり、両者の関係は一般的に次式となる
\begin{aligned}
\text{BEI}
&=
\text{期待インフレ率} \\
&\qquad \qquad
+ \underbrace{\text{インフレ リスクプレミアム}}_{\text{Risk Premium}}
+ \underbrace{\text{流動性プレミアム}}_{\text{Liquidity Premium}}
\end{aligned}
- 右辺の2，3項目の計測はかなり困難で、筆者は
BEI ≒ 期待インフレ率と見做している。ただし次の点を忘れないように！- 物価連動債は流動性が低く、ショック時に BEI は急低下する
- この現象は、期待インフレ率の低下ではなく、流動性プレミアムの変動となり、
BEI ≠ 期待インフレ率となる
2. 物国30回債のBEI計算例
- では 計算例を示そう。下図はJSDAが発表した2026年1月6日引けのマーケットデータ。(左上の2026年1月7日とは翌日に発表する日付を意味)
- 867行目の物国30回債のクーポンが
*印で表示されているが、正しくは0.005% - 164行目がベンチマークの378回債
- 867行目の物国30回債のクーポンが
$\qquad\qquad\qquad\qquad\qquad\qquad$(図5-1：JSDA 2026年1月6日引けデータ)
-
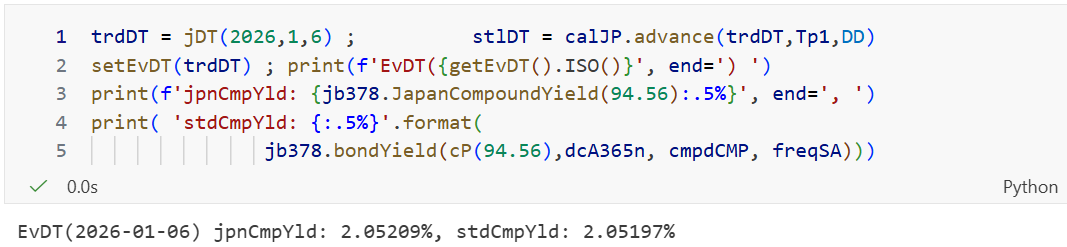
第2回記事 JGBクラスの日本式複利メソッドの実装 で伝えたように、JSDAはT+0で日本式複利を計算し、2.051%
-
下のセルでは、第2回記事の復習を兼ね、T+0で378回債の価格94.56から日本式と欧米式複利を計算した
- 3行目のmakeJGB関数は第2回 4節の説明を参照
- この関数の引数は最低3つ必要となり、
(378回債の前回利払日、満期日、クーポン)で構成 - 5行目
getEvDT関数はQuantLibのシステム日付を取得する関数として、新たにmyABBRモジュールに追加(これでsetter, getterが揃った) - 第2回記事でも記したが、日本式複利と欧米式複利の差は大きくない。問題がない場合、筆者の投稿はQuantLib標準の複利メソッドを使用する
-
T+0は邪魔なので、次のセルは通常のT+1で複利を算出させた
- 2行目のsetEvDT関数で、取引日
(trdDTはtrade dateの略)を1月6日にセットし直し、複利利回り 2.052%を算出
- 2行目のsetEvDT関数で、取引日
- これらを前提に次のセルで BEI 1.7770% を算出
-
上で算出した各複利利回りは第2回記事の復習であり、本題からはズレている
-
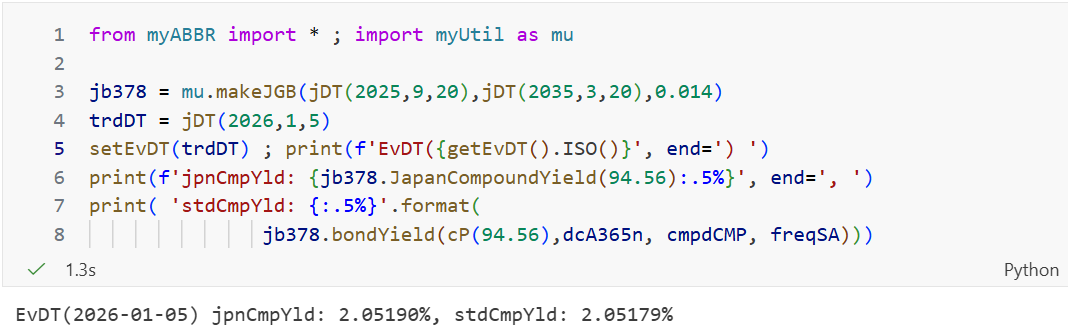
BEIの計算は下のたった10行のコードのみで完了する
$\qquad\qquad\qquad\qquad$(図5-2：実質利回り債オブジェクトとBEI算出) -
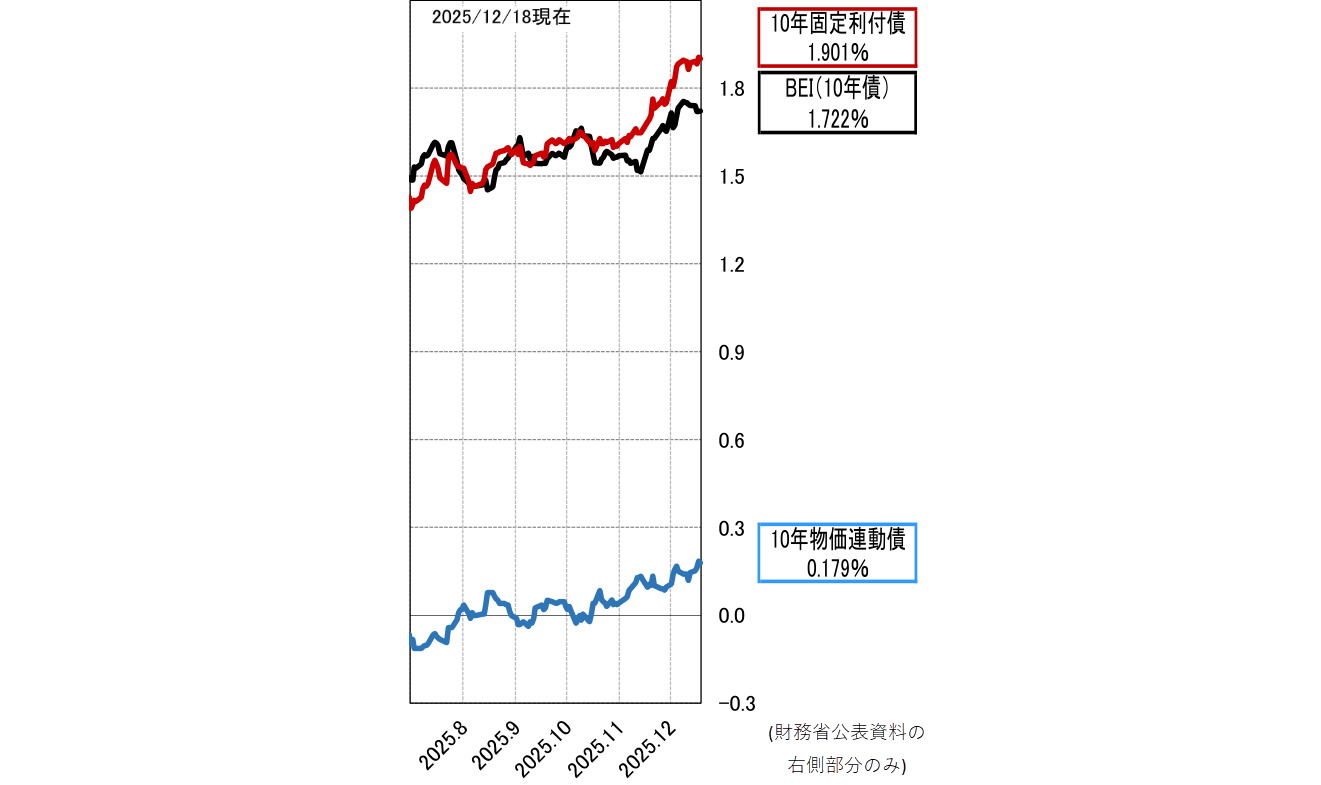
日本の財務省は「ブレーク・イーブン・インフレ率の推移」を物価連動国債のWebで発表しているが、2025/12/18現在で1.722%と公表し、ほぼ同じ水準
(注：評価日が異なる)
-
- では上のコードを概観する
- 2,3行目は初期値の設定
-
effDT,matDTは物国30回債の前回利払日と満期日 -
rBndPRC,nmlYldは それぞれreal yield bond price(実質利回り債の価格), nominal yieldの略
-
- 6行目は
makeJGB関数を使い、インフレで元本が増減しない実質利回り債のオブジェクトrBndOBJを物国30回債の条件から設定-
rBndOBJとはクーポン0.005%、償還100円の国債
-
- 8行目はJSDAの価格 97.55からYTM利回り 0.2750% を算出
-
cP(...)関数はクリーンプライスを意味し、myABBRモジュールで定義 - この97.55は実質利回り債の価格なので、Real clean price
(実質価格)と呼ばれる
-
- 9行目は YTMベースの式(1)を使い、BEI 1.777%を算出
- このBEI値は第6回記事で利用するので、変数
beiRTに保存
- このBEI値は第6回記事で利用するので、変数
- 2,3行目は初期値の設定
QuantLibを使えば、BEIは驚くほど簡単に計算できることが判ったと思う。
まとめ
- BEIを定義し、YTMベースのBEI算出のコード例を示した
- そのコードでは実質利回り債を第2回記事で作成したmakeJGB関数で作成
- 上記コードはテキストのサポートページ より、取得可能。
(ファイル名はinfBond-JP.ipynb, myABBR.py, myUtil.py)(ファイル名はinfBond-JP.ipynbへ修正し、第6回コードが含まれる