0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@retrieveram(レトリバー am)

第6回：物価連動国債のキャッシュフローと名目利回り

Last updated at Posted at 2026-01-21

第5回記事ではYTMベースのBreak-even Inflation (以下BEI)を算出した。今回はBEIでインフレが発生した場合 (つまり 前回算出した1.777%で、インフレが発生した場合)、物価連動国債 (以下 物国) の名目利回りはベンチマーク国債の利回り 2.052%になるかを確認する。

この確認作業は、インフレ後の物国のキャッシュフローの作成と利回り算出となるが、この2つの作業は物国を理解する王道である。

かなり長い記事となり、我慢が必要となることを最初に断っておく。

1. Reference CPI (適用指数)、 Index Ratio (連動係数)

初めに物国のキャッシュフロー作成の下準備をする。

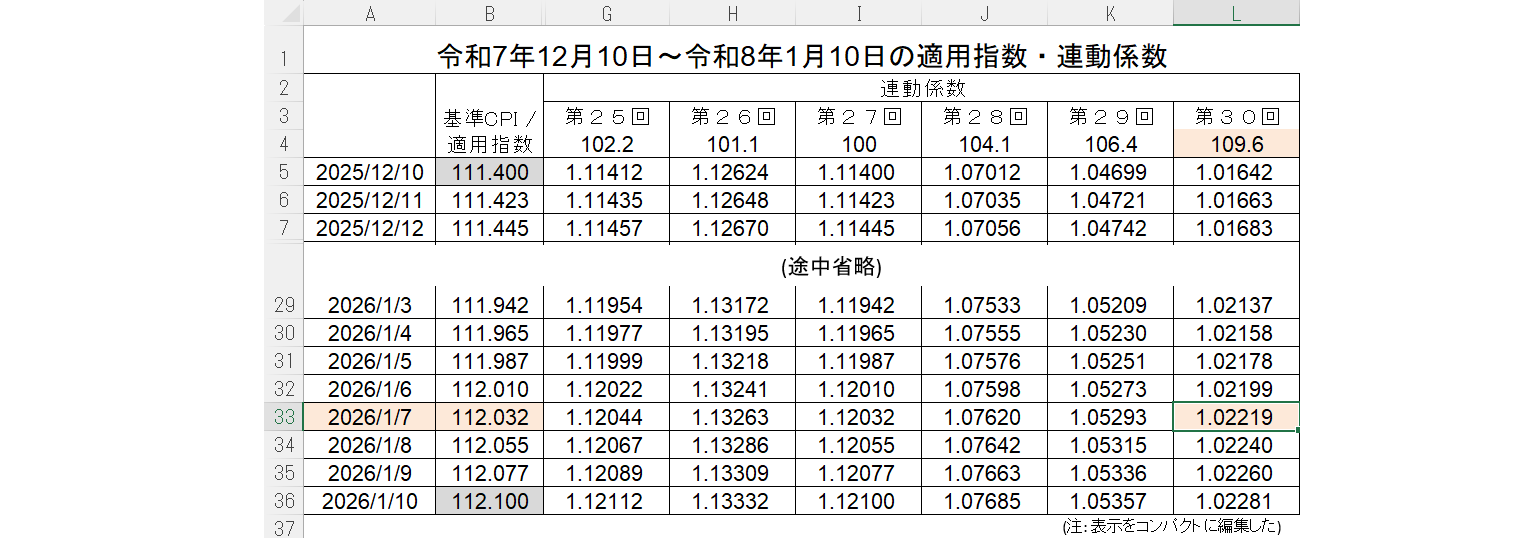
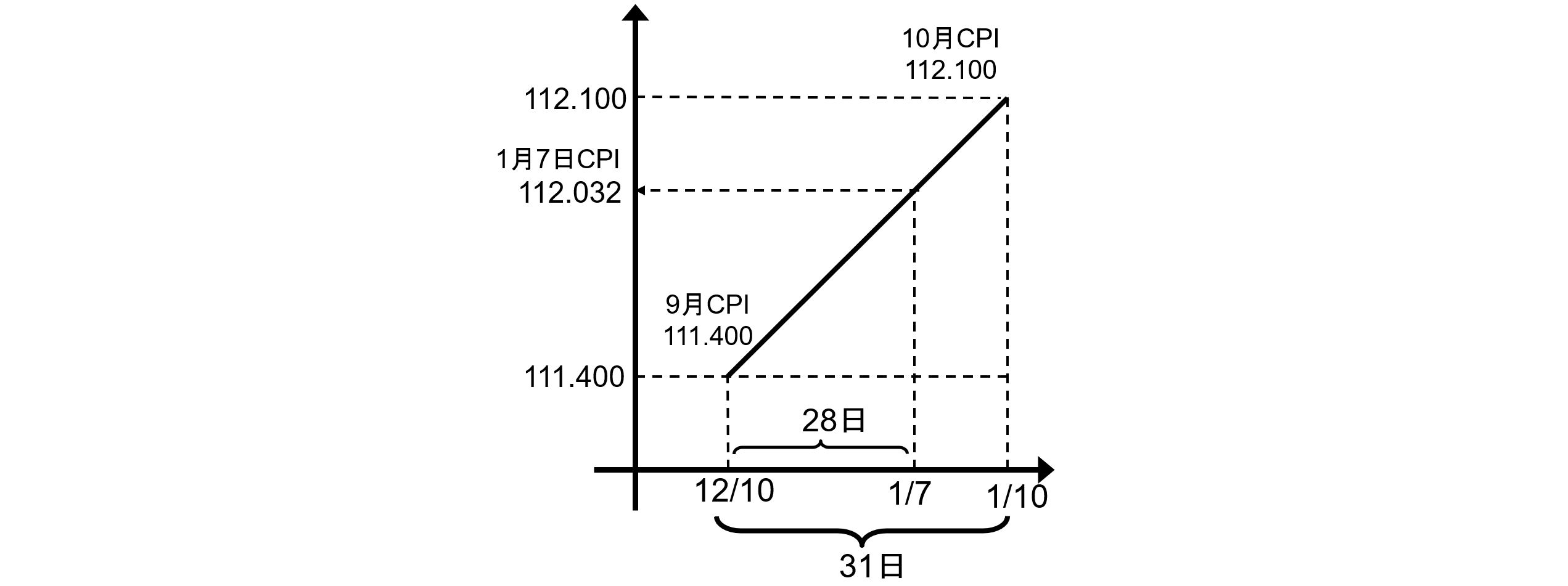
まず、このExcelについて 説明するが、物国の取引日 / 受渡日は前回同様 2026年1月6日 / 7日とする。重要な点は、受渡日のCPIがB33セルの112.032と算出されている点である。

1-1. Reference CPI (適用指数) B33セル：112.032

  • 物国が参照するCPIは3ヶ月前のデータ。このことを「3ヶ月ラグのCPI」などと言う

  • A5, B5セル： 2025/12/10 111.40は3ヶ月前の2025年9月10日のCPIが111.40を意味

  • 同様にA36, B36セル： 2026/1/10 112.10は3ヶ月前の2025年10月10日のCPIが112.10であった

    • 本来のCPIの解釈にしたがえば、9月CPIが111.40、10月CPIが112.10であり、9月10日や10月10日という各月10日のCPIではない
    • たぶん、この10日は物国の利払日が10日なため、適当に財務省が決めたものか？
    • 欧米の標準仕様は月初の1日で、この違いがあとあと コーディングに影響

  • 2025/12/11～2026/1/9の各日付けのCPIは111.40と112.10を単純に線形補間した値

    • これら補間したCPIを Reference CPI (適用指数)と呼ぶ

    • 下は2026年1月7日の適用指数計算のイメージ図
      日本12月CPI補間の図png

  • この線形補間は次式のように 初めにウエイト $w$ を算出し、

    $$
    w=\frac{1/7-12/10}{1/10-12/10}=\frac{28日}{31日}
    $$

    • この $w$ を利用して、

      $$
      (1-w) \times 111.400 + w \times 112.100 = 112.032
      $$

      • テキスト p.11 脚注4 式(1.3) に線形補間の原型の式を記したが、その右辺が上のウエイトに対応

      • このウエイト算出で注意すべき点は2025/12/10～2026/1/10を使うこと。3ヶ月ラグの期間 2025/9/10～10/10ではない (ここはよく間違える！)

      • 線形補間の式は使わないとすぐに忘れるので、メモしておく

        $$
        y(x)=(1-w)\ y_0+w\ y_1 ,\quad \text{ウエイト } w:=\frac{x-x_0}{x_1-x_0}
        \tag{6-1}
        $$

      • 同値な形： $ y(x)=y_0+\frac{x-x_0}{x_1-x_0}(y_1-y_0)
        \quad $(テキスト p.11 脚注4 と同じ式)

      • ウエイトは12/10からの経過日数に対応し、12/10では $w=0$ 、1/10では $w=1$

1-2. Base CPI (基準CPI) L4セル：109.6

  • G4～L4セル：102.2, ... , 109.6 物国25回債～30回債が発行された時のCPI

    • CPIの改定があれば、このBase CPIの値は改定されるが、それ以外は不変
    • 図6-1の2行目では、baseCPIとせず、発行時CPIとしてのissCPIという変数名を使用 (baseという用語が他の状況で使われるため)

1-3. Index Ratio (連動係数) L33セル：1.02219

  • Index Ratioは次式のように、Reference CPI ÷ Base CPIで算出

    • 発生したインフレの結果として、物国額面の増減を表す数値

    $$
    \text{Index Ratio (連動係数)}= \frac{
    \overset{(適用指数)}{Ref.CPI}
    }{
    \underset{(基本CPI)}{BaseCPI}
    } = \frac{112.032}{109.6} = 1.02219 \tag{6-2}
    $$

  • 上式では インフレーションにより、額面が1.0から1.02219に増加

1-4. 2つのクリーン価格：Real clean price と Clean price

  • 第5回 2節では市場で取引されている価格97.55を実質価格 (Real Clean Price)と呼んだ

  • 物国のClean Price (クリーン価格)はIndex Ratioを使い、次式で算出する

    $$
    \text{クリーン価格} = \text{Real Clean Price} \times \text{Index Ratio} \tag{6-3}
    $$

  • つまり、物国は2つの利回り(名目と実質)に対応し、2つのクリーン価格を持つ

  • 実質価格に対応し、クリーン価格を名目価格とも言う

  • このクリーン価格に経過利息を加算したものがダーティー価格であり、受渡代金となる (ダーティー価格は1つのみ)

2. CPI指数オブジェクト、 インフレカーブ オブジェクト

Reference CPI や Base CPI は大した計算を行っていないが、ここまでの部分をQuantLibで計算するには、インフレカーブを持ったCPI指数のオブジェクト(図6-1 10行目のcpiIX)を作成し、そのメソッドで計算させる。

  • インフレカーブとCPI指数の関係は、スワップカーブとIborの関係に対応

    • Iborのフォワードレートを計算する際、スワップカーブが必要
    • CPI指数のフォワードを計算させるのに、インフレカーブが必要
      • この回の目標であるインフレ後の物国キャッシュフローを作成するには、CPI指数のフォワードの計算が必須

  • 図6-1がコードと出力例 (見慣れないキャメルケースは"myABBRモジュールで定義"ではと考えよう)
    CPIオブジェクトpng $\qquad\qquad\qquad\qquad\qquad$(図6-1：CPIオブジェクトコード)

    • インフレ関連で新たに追加したmyABBRモジュールの短縮形
      myARRBCPIpng$\qquad\qquad\qquad\qquad\quad$(図6-2：myABBRでのインフレ関連の短縮形)

2-1. 出力に関連したコード

まず、図6-1の出力結果が第1節のReference CPI、Index Ratioと一致している点を確認しよう

  • 14行目 refCPI：CPIクラス(C++の構造体) の静的メソッドlaggedFixingで3ヶ月ラグでの2026年1月7日のReference CPIを算出 (静的メソッドはテキスト p.7を参照)

  • この新しいメソッドは最近追加されたようで、ドキュメントが間に合っていないが、QuantLib.pyファイルでは次のようなコード (QuantLib.pyファイルはテキスト p.7を参照)

deflaggedFixingpng

  • 引数は4つで、(CPIインデックス、ターゲットの日付、3ヶ月ラグ、補間方法)

  • 図6-1の14行目で与えた4つの変数から、これらの引数の内容を推測しよう。以下が簡単な説明 (ds9, lag3M, cpiLNRはmyABBRの短縮形、図6-2参照)

    • cpiIX：10行目で作成されたCPI指数のオブジェクト

    • aStlDT：adjusted settle dateの略で5行目で作成。

      • 本来の受渡日(stlDT)2026年1月7日から9日(ds9)を引いた日付 (dsはdaysの略)

    • lag3M：ラグ3ヶ月を意味する短縮形

      • ラグ0ヶ月のlag0MもmyABBRでは定義

    • cpiLNR：CPIの補間を線形に指定する短縮形 (LNRはlinearの略)

      • １ヶ月単位でCPIが更新されるため、月内を線形補間させる
      • 補間計算を行わないcpiFLTもmyABBRで定義

  • 14行目 右辺先頭のroundはCPI指数を少数3桁へラウンド (財務省ルール)

  • 15行目 ixRTO：Index Ratioを式(6-2)より、refCPI÷issCPI で算出

    • 先頭のroundでindex Ratioを少数5桁へラウンド (財務省ルール)

2-2. CPI指数オブジェクトのコード

では図6-2のコードを1行目から見て行く

  • 2,3行目 初期値設定：3ヶ月ラグで参照する9月と10月のCPIをstCPI, enCPIに設定 (st, enはstard, endの略)

    • Quantlibでは、CPIデータは月初～月末となるため、年、月という日付を与える

  • 5,6行目 ds9による調整：毎月10日というCPIの日付を欧米の標準仕様に修正すため、取引日と受渡日から9日(ds9)を引いて、aTrdDT, aStlDTに設定 (aはadjustedの略)

    • setEvDT(aTrdDT) によって、QuantLibのシステム日付も9日前に修正

    • この修正法は、1-1節で示した「適用指数計算のイメージ図」の日付を9日ずらしても同じ計算となり、結果は正しい

      • 国債の場合、利払い日・償還日が曜日に関係なく、固定されているため、このようなシフトが可能

  • 9,10,11行目 CPI指数オブジェクトの設定：ZeroInflationIndexコンストラクタによって、日本のCPI指数オブジェクト cpiIX を作成

    • コンストラクタの引数に関しては、QLPドキュメントの説明(下図)と10,11行目を見較べて、推測しよう (QLPドキュメントはテキスト p.6を参照)
      classZeroInflationIndexpng

      (若干の補足説明)

      • 第2引数 jpRegion：myABBRモジュールで、CustomRegionコンストラクタを使い、ql.CustomRegion("Japan", "JP")と定義
      • 第3引数 revisedF：myABBRモジュールで False を指定し、CPI指数が改定がされていないと設定
      • 第5引数 lag0M：インデックス自体にラグは無いので、myABBRモジュールで、ql.Period('0M')を設定
        • QLPドキュメントの説明とは異なる。ここをlag3Mにするとエラーで身動きできなくなる
      • 第7引数 infCvHDL：9行目で設定した空のインフレカーブ用ハンドル
        • インフレカーブの設定は2-3節で行う
        • 空のハンドルの設定はTiborと同じで、テキスト p.43の図2.3 7,8行目を参照

  • 12行目 cpiIX.addFixing：9月と10月に確定したCPI値をcpiIXオブジェクトに登録

    • addFixingメソッドはTiborと同じで、テキスト p.59 2.4.4節を参照
    • jDT(yy,mm,1)と毎月1日を指定$\quad$ (ここを10日にしても、1日でフィクシングされる)

  • 13行目 lastFixingDate：最後にフィクシングした日付を戻すメソッド

    • 12行目で9月と10月のCPI値をフィクシングさせたので、最後にフィクシングした日付は2025年10月1日

2-3. インフレカーブ 設定

直前に説明した13行目 lastFixingDateメソッドが意味することは「cpiIXオブジェクトは10月1日以降のインフレデータを持っていない」ことである。インフレカーブの設定は、その日付以降の将来のインフレ率をcpiIXに教える。

図6-3の2行目 ZeroInflationCurve はインフレカーブを作成する最も簡便なコンストラクタ。
ZeroInflationCurvepng$\qquad\qquad\qquad\qquad\qquad$(図6-3：インフレカーブ オブジェクト)

  • 3行目：日付リスト[enCpiDT,enCpiDT+pD('10y')]とレートリスト[beiRT,beiRT]を与えて、インフレカーブのオブジェクトinfCvOBJを作成

    • 日付リストでは、2025年10月1日から10年間を指定し、レートは第5回記事で計算したbeiRT=1.7770%をフラットで設定

  • 5行目 infCvHDL.linkTo(infCvOBJ)：図6-1の9行目で作成した空のハンドルinfCvHDLへinfCvOBJオブジェクトをリンク

    • infCvHDLハンドルはcpiIXオブジェクト作成時の引数であった (同図 11行目)
    • このリンクにより、cpiIXオブジェクトはフォワードCPIの算出が可能になる

  • 6～8行 infCvOBJ.nodes： 作成されたinfCvOBJオブジェクトは金利カーブと同様なnodesメソッドを持ち、nodes情報を出力 (nodesの例は、テキスト 図2.3など 参照)

3. 物国オブジェクトとプライシング

長い準備が終わり、図6-4の2～4行目で物国30回債用のインフレで元本が増大するオブジェクトの作成にたどり着けた。
CPIBond-No30.png$\qquad\qquad\qquad\qquad\quad$(図6-4：物国オブジェクトとプライシング)

初めに出力結果を確認する。

  • 物国の名目金利 nominal YLD は 2.05200%とベンチマーク国債の利回りとほぼ一致

    • どのような計算から、名目利回り 2.052%が計算されたかは、3-xx節で説明

  • 実質価格(Real Clean Price)を表すrealClnPRC=97.5728931は第5回記事 2節の97.55と0.02円ほどのズレ

    • この実質価格を97.55に一致させるため、BEIで設定したインフレカーブを修正する。この修正は第7回記事で説明

次にどのメソッドがこの計算結果を算出したかを確認する。(使用されている債券のメソッドの詳細はテキスト4.2節で説明済み)

  • 9行目の cleanPriceメソッドは、名目価格(Clean Price)を戻し、99.73804円

  • 実質価格は式(6-3)より、9行目 2つ目のコードでrClnPRC=clnPRC/ixRTOで手計算

  • 9行目で計算された名目価格 clnPRC を11行目の bondYieldメソッドに与え、名目利回り 2.052% を算出

3-1. CPIBond コンストラクタとメソッド

では 図6-4のコードで残った部分を確認する。

  • 2行 iScdOBJ： 第5回記事で使用したmakeJGB関数は使わず、Scheduleコンストラクタを使用し、物国30回債用のiScdOBJオブジェクトを作成

    • 注意すべきは、effDTとmatDTをds9で調整させている
    • その他はmakeJGB関数のScheduleコンストラクタと同じ

  • 3,4行 iBndOBJ ：CPIBondコンストラクタによって、物国30回債のiBndOBJを作成。

    このコンストラクタの引数に関しては、QLPドキュメントの説明 (下図)と3, 4行目を見較べて、推測しよう
    classCPIBond.png

    • 3番目の引数 growthOnly は常にFalseとし、図6-2でgwONY=False を設定

    • その他の引数は自明であろう

  • 6,7行：6行目でディスカウントカーブを作成し、7行目でiBndOBJオブジェクトにエンジンをセット

    • この手順はテキスト 図4.11 と同じ

    • 注意すべきはディスカウントカーブの受渡日がaStlDTとしている。つまりディスカウントカーブも9日間シフトさせている

  • テキスト 図4.11 ではNPVメソッドで利含み価格を計算させているが、エンジンを搭載した債券オブジェクトの場合、この図6-4の9,10行目のように cleanPrice, accruedAmount, dirtyPrice 等は引数無しで計算できる

3-2. 物国30回債のキャッシュフロー

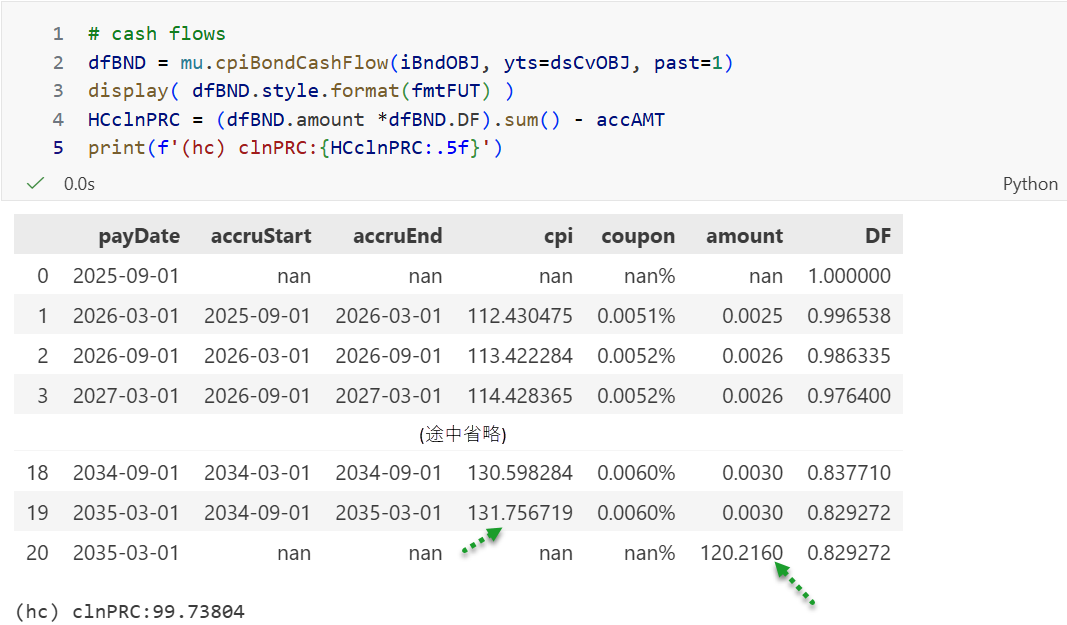
図6-5は 物国30回債のiBndOBJオブジェクトを用い、2, 3行目でキャッシュフロー表を出力させ、4行目でキャッシュフロー表のamount列とDF列から、クリーン価格を手計算させ、図6-4と同じ価格 99.73804を得た。
No30-CashFlow.png
$\qquad\qquad\qquad\qquad\quad$(図6-5：物国30回債キャッシュフロー表)

このキャッシュフロー表から、まず 理解すべき点を列挙しよう。

  • 左3列の日付は9日間シフトさせたもので、本来はすべてが10日

    • index20番の物国30回債の債券償還日は2035年3月10日

  • キャッシュフロー表 中央の cpi列 はBEI 1.7770%でインフレが発生した場合の将来のCPIで、Reference CPI(適用指数)

  • index20番は物国30回債の償還価格が 120.2160 を表示

    • この償還価格はIndex Ratio (連動係数)として、償還日CPI 131.756719 ÷ 発行時CPI 109.60 から算出

    • 各利払い日の元本の増大は利払い日CPIから、Index Ratioを計算し、利払い額が算出される

  • 図6-4で出力された名目利回り(nominalYLD) 2.0520% はamount列から計算した年2回複利

この第6回記事はかなり長くなったので、この辺りで一旦休憩し、残りは第7回記事で説明しよう。

  • 上記コードはテキストのサポートページ より、取得可能。(ファイル名はinfBond-JP.ipynb, myABBR.py, myUtil.py)
0
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
0
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?