非線形数理モデルであるHenon写像を紹介します。
以前に紹介したロジスティック写像と同じ低次元離散力学系です。
非線形の数理モデルであるエノン写像を対象として、初期値鋭敏性を確認します。
ロジスティック写像でも同様の記事をがあるのでぜひ!
関連記事1: ロジスティック写像の紹介
関連記事2: 初期値鋭敏性について(ロジスティック写像)
エノン写像は以下のような連立方程式, 漸化式で表されます。
$x_{n+1} = 1- ax_{n}^2 + y_{n}$
$y_{n+1} = bx_{n}$
$a,b$はエノン写像のパラメータになります。
本題の初期値鋭敏性の話に入っていきます。
初期値鋭敏性とは、カオスの定義あるいは特性の一つになります[1]。
初期値鋭敏性を実際に確認するために、$10^{-5}$や$10^{-10}$くらいの微小の誤差を与えます。
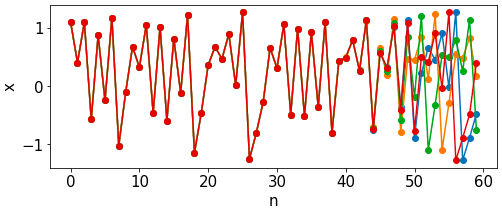
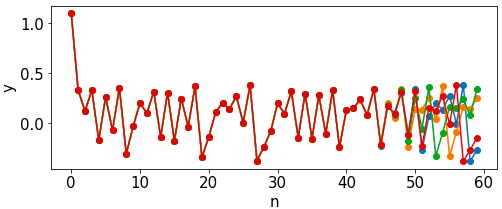
$10^{-5}$や$10^{-10}$程度の誤差ではありますが、途中から大きく軌道が外れるのが確認できると思います。
別の見方で軌道が大きく外れるのを確認してみます。
x軸が時間, y軸が誤差を表しています。
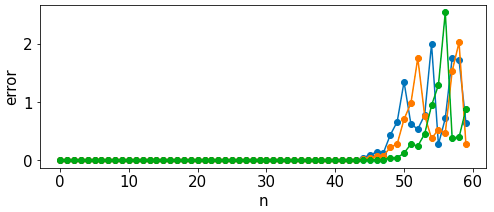
$n=40$くらいまでは軌道はほとんど一緒に見えますが、$n=45$くらいから大きく軌道が外れることがわかります。