以前(というか昨年のAdvent Calender)線形SVMについて書かせていただいたのですが、非線形の部分に触れられずに終わってしまったので、今回は続きということで非線形SVMについてまとめてみようと思います。
前回の記事は以下になります。
線形SVM(Machine Learning Advent Calendar 2015)
非線形SVMとは
前回の線形SVMでは、データ集合の実空間上に線形な境界を設けることで、データ集合を2つのグループに分類していました。
例えば、二次元空間上に存在するデータ集合を2つのグループに分類したいとき、線形SVMを使えば両グループが最も乖離する位置に線形な境界(超平面)を定義でき、データ集合を2分することができます(なおこのときのデータ集合は訓練集合であり、各データの正解ラベルはわかっているものとします)。
 (同じ色の点は、同じグループのデータであることを表しています)
(同じ色の点は、同じグループのデータであることを表しています)
では、この実空間上の超平面を作る線形SVMは、どんなデータ集合も分離できるのでしょうか?

例えば、二次元空間上のデータ集合が上図のように分布していた場合、どんな直線の引き方をしてもデータ集合を2つに分けられそうにありません。
このように、ソフトマージンによる制約緩和があるとはいえ、全てのデータを超平面だけで分離するには限界があります。
そこで非線形SVMでは、一旦実空間のデータを超平面で分離できる空間に写像してから、線形SVMと同じ仕組みでデータ集合を分離します。

超平面でデータ集合が分離できることを線形分離可能といいます。写像後の空間で線形分離可能であれば、その空間内で線形SVMの考え方を適用すればよいという、至ってシンプルな考え方です。
ここで気になるのが、写像の方法です。非線形SVMでは、線形SVMで扱った制約付きの目的関数の最適化を別の形で表現します。前者を主問題、後者を双対問題と呼びます。この双対問題の中で、非常にエレガントな形で別空間への写像が行われます。
次項では、この双対問題について説明します。
双対問題
ソフトマージンを適用した線形SVMにおける主問題は、以下の様なものでした。
\min _{\boldsymbol{w},b,\boldsymbol{\xi} }\frac{1}{2}{{\|\boldsymbol{w}\|}^2+C\sum_{i \in \{1...n\} }ξ_i \ \ \ \ } \\
\mbox{ s.t. } y_i(\boldsymbol{w^{\mathrm{T}}x_i}+b) \geq 1-ξ_i \ \ \ (i \in \{1...n\}), \ \ \ ξ_i \geq 0
簡単に説明すると、境界に最も近いデータ点と境界の距離が、なるべく離れるようにしたい・・・という意図が、この主問題に落とし込まれています。
(正規化等行ったので、わかりづらくなっていますが。。。)
この主問題を、ラグランジュの未定乗数法を使って解いていきます。
ラグランジュの未定乗数法
ラグランジュの未定乗数法とは、制約条件の与えられた目的関数を最適化したいとき、新しい目的関数を作り最適化する手法です。
大まかに説明すると、パラメタ$\boldsymbol x$に関して最適化を行う目的関数を$f(\boldsymbol x )$、制約条件を$g_k(\boldsymbol x )$(制約条件は一つ以上存在)とおいた時、
F(\boldsymbol \lambda , \boldsymbol x)=f(\boldsymbol x )-\sum _k \lambda_k g_k(\boldsymbol x )
を新たな目的関数とします。但しこの時、$g(\boldsymbol x)$の右辺は0である必要があります。
$\lambda _k$はラグランジュ乗数と呼び、制約条件の数だけ定義されます。なおここでは、ラグランジュ乗数も目的関数の中で最適化すべきパラメタとなります。ラグランジュの未定乗数法を使うことで、制約ごと目的関数の中に組み込むことができ、制約のない目的関数の最適化問題に落とし込むことができます。
このように目的関数を作り直せる理由については、上記リンク先の幾何的解釈が参考になります。
ラグランジュの未定乗数法による双対問題の導出
先程のラグランジュの未定乗数法を主問題に適用するために、主問題の目的関数と制約条件を以下のように関数の形で表記します。
\begin{aligned}
f(\boldsymbol w, \boldsymbol \xi ) & =
\frac{1}{2}{{\|\boldsymbol{w}\|}^2+C\sum_{i \in \{1...n\} }ξ_i \ \ \ \ } \\
\\
g(\boldsymbol w, b, \xi _i) & =
y_i(\boldsymbol{w^{\mathrm{T}}x_i}+b) -1+ξ_i \geq 0 \\
\\
h(\xi _i) & = ξ_i \geq 0 \\
\\
& i \in \{1...n\} \\
\end{aligned}
2つの制約条件に対応する関数を$g(\boldsymbol w, b, \xi _i)$と$h(\xi _i)$で表しています。
ただし、各関数は$\xi _i$の個数分だけ定義されるので、$g(\boldsymbol w, b, \xi _i)$と$h(\xi _i)$はそれぞれ$n$個存在することになります。
そしてラグランジュ乗数 $\boldsymbol \alpha = ${$ \alpha _1,...,\alpha _n $}$, \ \boldsymbol \mu = ${$ \mu _1,...,\mu _n $}を用いて、新しい目的関数を以下のように定義します。
なお各乗数は非負であるとします。
L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu) = \ \
f(\boldsymbol w, \boldsymbol \xi ) \ \ -
\sum _{i \in \{1...n\}} \alpha _i g(\boldsymbol w, b, \xi _i) \ \ -
\sum _{i \in \{1...n\}} \mu _i h(\xi _i)
= \frac{1}{2}{{\|\boldsymbol{w}\|}^2+C\sum_{i \in \{1...n\}}ξ_i}\ \ -
\sum _{i \in \{1...n\}} \alpha _i \{ y_i(\boldsymbol{w^{\mathrm{T}}x_i}+b) -1+ξ_i \}\ \ -
\sum _{i \in \{1...n\}} \mu _i \xi _i
最適化すべきパラメタがだいぶ増えてきました。
以降は説明のため、主問題で登場したパラメタ$\boldsymbol w, b, \boldsymbol \xi$を主変数、ラグランジュ変数$\boldsymbol \alpha , \boldsymbol \mu$を双対変数と呼ぶことにします。
新しい目的関数ができたら、次は関数$L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu)$のうち、双対変数に関して最大化した関数$P(\boldsymbol w, b, \boldsymbol \xi)$を定義します。
P(\boldsymbol w, b, \boldsymbol \xi) =
\max _{\boldsymbol \alpha \geq \boldsymbol 0 \ , \
\boldsymbol \mu \geq \boldsymbol 0}
L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu)
= \frac{1}{2}{{\|\boldsymbol{w}\|}^2+C\sum_{i \in \{1...n\}}ξ_i} \ \ -
\max _{\boldsymbol \alpha \geq \boldsymbol 0 \ , \
\boldsymbol \mu \geq \boldsymbol 0} \{
\sum _{i \in \{1...n\}} \alpha _i \{ y_i(\boldsymbol{w^{\mathrm{T}}x_i}+b) -1+ξ_i \}\ \ -
\sum _{i \in \{1...n\}} \mu _i \xi _i
\}
$ \max _{ \boldsymbol \alpha \geq \boldsymbol 0 , \boldsymbol \mu \geq \boldsymbol 0 } $で囲まれた項は元々は制約条件でした。
もし$ y _i ( \boldsymbol w ^{\mathrm{T}} x_i + b ) -1 + ξ _i \lt 0$または$\xi _i \lt 0$であった場合、関数$L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu)$は無限大に増加してしまい、最大値が存在しなくなってしまいます(双対変数は非負)。
逆に$ y _i ( \boldsymbol w^{\mathrm{T}} x_i + b ) -1 + ξ _i \geq 0$または$ \xi _i \geq 0$が成立すれば、$ \max _{ \boldsymbol \alpha \geq \boldsymbol 0 , \boldsymbol \mu \geq \boldsymbol 0 }$で囲まれた項の最大値は0となり、$P(\boldsymbol w, b, \boldsymbol \xi)$元の目的関数が出現します。
よって、制約条件を満たしているときのみ、$P(\boldsymbol w, b, \boldsymbol \xi)$は最適化可能になります。
このことから、$P(\boldsymbol w, b, \boldsymbol \xi)$を主変数について最小化した
\begin{aligned}
\min _{\boldsymbol w, b, \boldsymbol \xi} P(\boldsymbol w, b, \boldsymbol \xi) =
\min _{\boldsymbol w, b, \boldsymbol \xi} \max _{\boldsymbol \alpha \geq \boldsymbol 0 \ , \ \boldsymbol \mu \geq \boldsymbol 0}
L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu)
& \ \ \ (1)
\end{aligned}
は、元の制約付き目的関数の問題と等価であるといえます。
これで、制約のない目的関数を最適化する問題に帰着できることが確認できました。
D(\boldsymbol \alpha, \boldsymbol \mu) =
\min _{\boldsymbol w, b, \boldsymbol \xi}
L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu)
更にこの$D(\boldsymbol \alpha, \boldsymbol \mu)$を双対変数に関して最大化します。
\begin{aligned}
\max _{\boldsymbol \alpha \geq \boldsymbol 0 \ , \ \boldsymbol \mu \geq \boldsymbol 0} D(\boldsymbol \alpha, \boldsymbol \mu) =
\max _{\boldsymbol \alpha \geq \boldsymbol 0 \ , \ \boldsymbol \mu \geq \boldsymbol 0}
\min _{\boldsymbol w, b, \boldsymbol \xi}
L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu)
& \ \ \ (2)
\end{aligned}
先程の$\min _{\boldsymbol w, b, \boldsymbol \xi} P(\boldsymbol w, b, \boldsymbol \xi)$は最終的に主変数に関する最適化を行う主問題でしたが、$\max _{\boldsymbol \alpha \geq \boldsymbol 0 \ , \ \boldsymbol \mu \geq \boldsymbol 0} D(\boldsymbol \alpha, \boldsymbol \mu)$は双対変数に関する最適化を行っています。
この$\max _{\boldsymbol \alpha \geq \boldsymbol 0 \ , \ \boldsymbol \mu \geq \boldsymbol 0} D(\boldsymbol \alpha, \boldsymbol \mu)$を双対問題と呼びます。
この問題を整理すると、双対変数のみの問題として表すことができます。
主変数の中身を求めるため、$\min _{\boldsymbol w, b, \boldsymbol \xi}L(\boldsymbol w, b, \boldsymbol \xi, \boldsymbol \alpha , \boldsymbol \mu)$を各主変数で偏微分し、それらを0とします。
\begin{aligned}
\frac{\partial L}{\partial \boldsymbol w} & =
\boldsymbol w - \sum _{i \in \{1...n\}} \alpha_i y_i x_i = 0 & (3)\\
\frac{\partial L}{\partial b} & =
- \sum _{i \in \{1...n\}} \alpha_i y_i = 0 & (4)\\
\frac{\partial L}{\partial \xi_i} & =
C - \alpha_i - \mu_i = 0 & (5)\\
\end{aligned}
$\boldsymbol w$の値は明らかです。$L$は$\boldsymbol w$に関する凸二次関数なので、$(3)$で得られた$\boldsymbol w$により$L$は最小になります。一方、$\xi_i$や$\mu_i$は上記方程式に現れていません。これでは任意の値をこれら2つの主変数に設定できてしまうため、各変数の係数が0でない限り$L$は無限に小さくなってしまいます。そこで$(4),(5)$を係数として使い、$\xi_i$と$\mu_i$を$L$から消去します。
L = \frac{1}{2} ||\boldsymbol w||^2 -
\sum _{i \in \{1...n\}} \alpha_i y_i \boldsymbol w^{\mathrm{T}} \boldsymbol x_i-
b \sum _{i \in \{1...n\}} \alpha_i y_i +
\sum _{i \in \{1...n\}} \alpha_i +
\sum _{i \in \{1...n\}}(C - \alpha_i - \mu_i)\xi_i \\ =
- \frac{1}{2} \sum _{i,j \in \{1...n\}} \alpha_i \alpha_j y_i y_j \boldsymbol x_i^{\mathrm{T}} \boldsymbol x_j + \sum _{i \in \{1...n\}} \alpha_i
無事主変数を消すことに成功しましたが、双対変数である$\boldsymbol \mu$も消えてしまいました。ですが方程式$(5)$より、$C - \alpha_i = \mu_i$が導けます。また双対変数は非負、すなわち$\alpha_i \geq 0 , \mu_i \geq 0$なので、$C - \alpha_i \geq 0$、さらに$C \geq \alpha_i \geq 0$であることが導けます。また$(4)$も制約条件として加えると、双対問題は新たに以下のように定義できます。
\max _ \boldsymbol \alpha
- \frac{1}{2} \sum _{i,j \in \{1...n\}} \alpha_i \alpha_j y_i y_j \boldsymbol x_i^{\mathrm{T}} \boldsymbol x_j + \sum _{i \in \{1...n\}} \alpha_i \\
\mbox{ s.t. } \sum _{i \in \{1...n\}} \alpha_i y_i = 0 , \ \ \ C \geq \alpha_i \geq 0 \ \ \ (i \in \{1...n\})
$(1)$は元の主問題と等価であり、$(1)$と$(2)$も$\max$と$\min$の順序が異なるだけで等価です。したがって上記の双対問題も元の主問題と等価であるといえます。
カーネルによる非線形空間への写像
前項で導出した双対問題から、SVMを非線形に拡張します。
$d$次元空間上の入力ベクトル$\boldsymbol x(\in \mathrm{R}^d)$をある特徴空間$F$へと写像する関数$\phi(\boldsymbol x)$を考えます。
この時、$\phi(\boldsymbol x)$を新たな特徴ベクトルとして$F$中の超平面は以下のように表されます。
f(\boldsymbol x) = \boldsymbol w^{\mathrm{T}} \phi (\boldsymbol x) + b
上記式では$\boldsymbol w$も$F$上のパラメータとなります。
$\boldsymbol x$が$\phi (\boldsymbol x)$となったことで、$F$上では線形であり、実空間$\mathrm{R}^d$上では非線形な$f(\boldsymbol x)$が定義されます。
この変換を先の双対問題にも適用すると、
\max _ \boldsymbol \alpha
- \frac{1}{2} \sum _{i,j \in \{1...n\}} \alpha_i \alpha_j y_i y_j \phi (\boldsymbol x)^{\mathrm{T}} \phi (\boldsymbol x_j) + \sum _{i \in \{1...n\}} \alpha_i \\
\mbox{ s.t. } \sum _{i \in \{1...n\}} \alpha_i y_i = 0 , \ \ \ C \geq \alpha_i \geq 0 \ \ \ (i \in \{1...n\})
となります。
この双対問題では、$\phi (\boldsymbol x)$が内積としてのみ出現しています。これはつまり、直接$\phi (\boldsymbol x_j)$を求めずとも、その内積形である$\phi (\boldsymbol x)^{\mathrm{T}} \phi (\boldsymbol x_j)$さえ計算できれば最適化が可能であることを暗に示しています。
そこで、この内積形$\phi (\boldsymbol x)^{\mathrm{T}} \phi (\boldsymbol x_j)$をカーネル関数
K(\boldsymbol x_i, \boldsymbol x_j ) =
\phi (\boldsymbol x)^{\mathrm{T}} \phi (\boldsymbol x_j)
として定義します。
ある特定の性質を満たす関数を用いることで、$\phi (\boldsymbol x)$を直接計算せずとも$K(\boldsymbol x_i, \boldsymbol x_j )$が計算できることが既にわかっているそうです(カーネルトリック)。
内積形をカーネル関数に置き換えた最終的な双対問題は以下のようになります。
\max _ \boldsymbol \alpha
- \frac{1}{2} \sum _{i,j \in \{1...n\}} \alpha_i \alpha_j y_i y_j K(\boldsymbol x_i, \boldsymbol x_j ) + \sum _{i \in \{1...n\}} \alpha_i \\
\mbox{ s.t. } \sum _{i \in \{1...n\}} \alpha_i y_i = 0 , \ \ \ C \geq \alpha_i \geq 0 \ \ \ (i \in \{1...n\})
これで、入力データの実空間上に、SVMによる非線形な超平面を作ることができます。
なおカーネル関数の持つべき性質について、あまり詳しいことは述べられませんが、
大体次のような性質を持つようです。
- 対称性を持つこと ($K(\boldsymbol x_i, \boldsymbol x_j ) = K(\boldsymbol x_j, \boldsymbol x_i )$)
- 正定値性を持つこと (任意の実数 $a_i,a_j$ について $ \sum_i a_i a_j K( \boldsymbol x_i, \boldsymbol x_j ) \gt 0$が成り立つ)
(正定値に関する事柄はまだ詳しく理解できていないので、また別の記事でまとめるかもしれません。。。)
また、代表的なカーネルとして、以下のものがよく用いられるそうです。
- RBFカーネル
K(\boldsymbol x_i, \boldsymbol x_j ) = exp(- \gamma ||\boldsymbol x_i - \boldsymbol x_j ||) \ \ \ (\gamma \in \mathrm R, \gamma \gt 0)
- 多項式カーネル
K(\boldsymbol x_i, \boldsymbol x_j ) = ( 1 + \boldsymbol x_i^{\mathrm{T}} \boldsymbol x_j ) ^ p \ \ \ (p \in \mathrm R)
- 線形カーネル(線形SVMと同じ)
K(\boldsymbol x_i, \boldsymbol x_j ) = \boldsymbol x_i^{\mathrm{T}} \boldsymbol x_j
- シグモイドカーネル(正定値ではないが、使われることが多い)
K(\boldsymbol x_i, \boldsymbol x_j ) = \tanh (c \boldsymbol x_i^{\mathrm{T}} \boldsymbol x_j + \theta ) \ \ \ (c, \theta \in \mathrm R)
Pythonによる実装
最後に、簡単ですがSVMによる手書き文字認識のpythonコードを掲載します。
機械学習に詳しい方ならご存知かと思いますが、scikit-learnと呼ばれる機械学習のライブラリを使えば、機械学習でよく用いられる前処理・データの選定・分類器、結果検証等の手法を簡単に試すことができます。
ここまでSVMの仕組みを追ってきてライブラリ頼みなのも情けない感じですが、
仕組みを抑えた上でこういった便利なライブラリを使っていくと実験が非常に捗るので、おすすめです。
from __future__ import print_function
import itertools
import numpy as np
from sklearn import svm
from sklearn.datasets import load_digits
from sklearn.cross_validation import train_test_split
from sklearn.grid_search import GridSearchCV
from sklearn.metrics import confusion_matrix
import matplotlib.pyplot as plt
# 手書き数字文字データセット(10class)
digits = load_digits(n_class=10)
# 特徴ベクトルと正解ラベル
X, Y = digits.data, digits.target
# データセットを交差検証によって訓練データ・テストデータへ分割
x_train, x_test, y_train, y_test = train_test_split(X, Y, test_size=0.4, random_state=0)
# 線形なSVMによる分類器(ソフトマージンにおける定数はC=1.)
clf = svm.SVC(kernel='linear', C=1.)
# clf = svm.SVC(kernel='rbf', gamma=0.001) # 非線形SVM, rbfカーネル
# 訓練データによる学習(超平面の決定)
clf.fit(x_train, y_train)
# テストデータの分類
pred = clf.predict(x_test)
# テストデータ分類精度
print ("Test Accuracy : ", (pred == y_test).mean())
#
# 混同行列(クラス分類の結果を可視化する行列)の表示
#
c_mat = confusion_matrix(y_test, pred)
plt.imshow(c_mat, interpolation='nearest', cmap=plt.cm.Greens)
plt.xlabel('Predicted labels')
plt.ylabel('True labels')
plt.grid(False)
plt.colorbar()
n_class = len(digits.target_names)
marks = np.arange(n_class)
plt.xticks(marks, digits.target_names)
plt.yticks(marks, digits.target_names)
# 分類データ数テキストラベル
thresh = c_mat.max() / 2.
for i, c in enumerate(c_mat.flatten()):
color = "yellow" if c > thresh else "black"
plt.text(i / n_class, i % n_class, c, horizontalalignment="center", color=color)
plt.tight_layout()
plt.show()
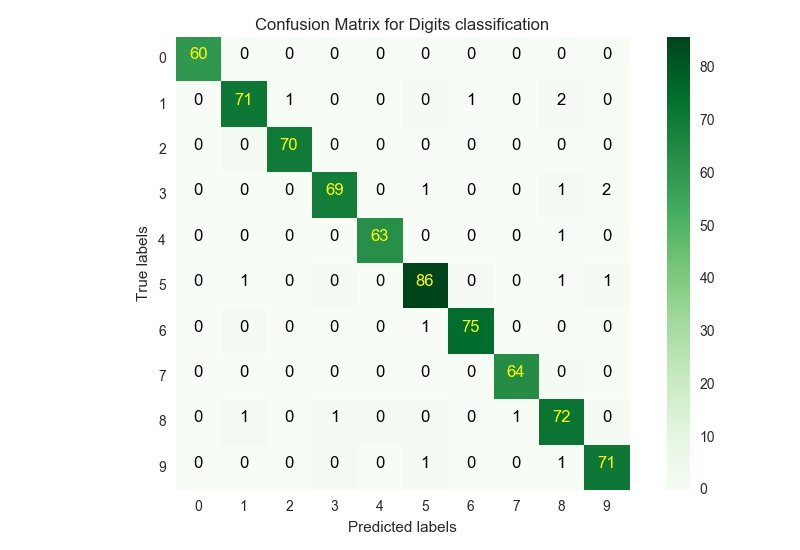
上記コードを線形カーネルで実行すると、出力は以下のようになります。
Test Accuracy : 0.974965229485
混同行列は以下のようになりました。
線形カーネルでも、概ね精度よく分類されているのがわかります。
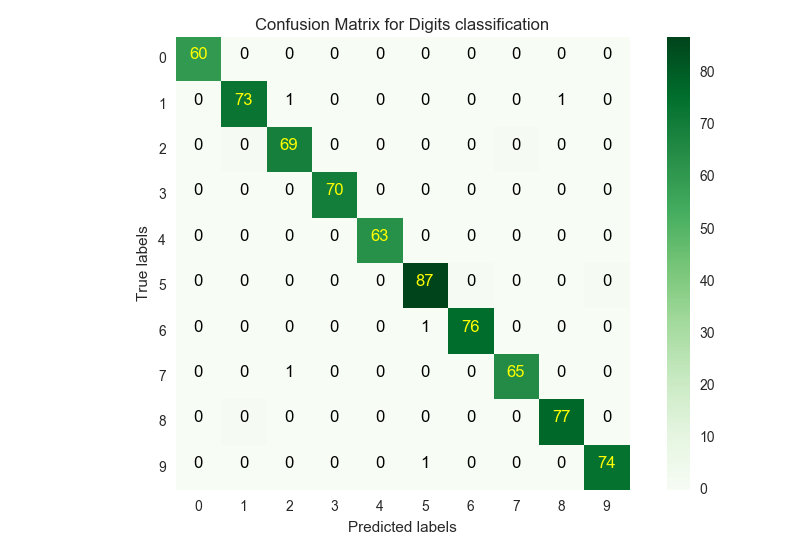
ここで、カーネルを非線形なRBFカーネルに変更し、再び学習・テストを行うと、精度と混同行列は以下のようになりました。
Test Accuracy : 0.993045897079
RBFカーネルにすることで、さらに精度良く分類することができました。
但し注意しなければならないのは、非線形にすることで必ずしも精度は向上するわけではないということです。非線形SVMのように自由度の高い学習モデルは、データに合わせて柔軟にフィッティングできる分、訓練データに過度にフィットしてしまう可能性が高くなります(過学習)。
なので実際には、複数のパラメタを検証する、データセットを増やすなどして、データセットに対して適した学習器(SVM)を決定する必要があります。また多角的に分類結果を検証する場合、単にテストデータに対する精度だけでなく、他の性能評価尺度を導入する必要があります。また、上記コードではtest_train_split関数でデータセットを単純に二分割していますが、限られたデータセットできちんと分類実験をしたい場合は交差検証を行う必要があります。
さいごに
今回の記事で、非線形な境界の作り方までは簡単ですがなんとか押さえられました。
個々の細かい理論がまだ十分理解できていないので、これから少しずつ追っていこうと思います。