\newcommand \iddots {
\mathinner {
\kern{1.2mu}
\raise{2mu}{.}
\kern{3mu}
\raise{7.4mu}{.}
\kern{3mu}
\raise{12.8mu}{.}
\kern{1.2mu}
}
}
\newcommand{\add}{\operatorname{add}}
\newcommand{\double}{\operatorname{double}}
\newcommand{\multiply}{\operatorname{multiply}}
\newcommand{\exponentiate}{\operatorname{exponentiate}}
\newcommand{\predecessorOf}{\operatorname{predecessorOf}}
\newcommand{\subtract}{\operatorname{subtract}}
\newcommand{\isZero}{\operatorname{isZero}}
\newcommand{\isLessThanOrEqualTo}{\operatorname{isLessThanOrEqualTo}}
\newcommand{\isGreaterThanOrEqualTo}{\operatorname{isGreaterThanOrEqualTo}}
\newcommand{\ifThenElse}{\operatorname{ifThenElse}}
\newcommand{\and}{\operatorname{and}}
\newcommand{\or}{\operatorname{or}}
% 名前なんとかならんもんか(\not を \renewcommand すると \neq にも影響してしまう)
\newcommand{\myNot}{\operatorname{not}}
\newcommand{\isEqualTo}{\operatorname{isEqualTo}}
\newcommand{\isLessThan}{\operatorname{isLessThan}}
\newcommand{\isGreaterThan}{\operatorname{isGreaterThan}}
\newcommand{\remainderOf}{\operatorname{remainderOf}}
\newcommand{\divide}{\operatorname{divide}}
\newcommand{\isDivisibleBy}{\operatorname{isDivisibleBy}}
\newcommand{\nthRootOf}{\operatorname{nthRootOf}}
\newcommand{\forAll}{\operatorname{forAll}}
\newcommand{\forAny}{\operatorname{forAny}}
\newcommand{\isPrime}{\operatorname{isPrime}}
\newcommand{\countPrimes}{\operatorname{countPrimes}}
\newcommand{\nthPrime}{\operatorname{nthPrime}}
\newcommand{\squareRootOf}{\operatorname{squareRootOf}}
\newcommand{\cubicRootOf}{\operatorname{cubicRootOf}}
\newcommand{\Ack}{\operatorname{Ack}}
\newcommand{\encode}{\operatorname{encode}}
\newcommand{\decode}{\operatorname{decode}}
\newcommand{\lengthOf}{\operatorname{lengthOf}}
\newcommand{\subscript}{\operatorname{subscript}}
\newcommand{\finalIndexOf}{\operatorname{finalIndexOf}}
\newcommand{\lastOf}{\operatorname{lastOf}}
\newcommand{\AckSeq}{\operatorname{AckSeq}}
\newcommand{\pushed}{\operatorname{pushed}}
\newcommand{\popped}{\operatorname{popped}}
\newcommand{\hyper}{\operatorname{hyper}}
TL;DR(この記事のまとめ)
アッカーマン関数は、原始再帰的でないが全域 $\mu$ 再帰的であるという点で意義深い関数です。
アッカーマン関数とは
この記事を開いてくださった方はアッカーマン関数についてはもうご存知かもしれませんが、そうでない方もいらっしゃるかもしれないのでここでご紹介いたします。
アッカーマン関数は、超巨大な自然数を生み出してしまうことで有名な関数です。その値の一例を見てみましょう。
\displaylines {
\Ack(0, 0) = 1 \\
\Ack(3, 4) = 125 \\
\Ack(4, 1) = 65533 \\
\Ack(4, 2) = 2^{65536} - 3 \ (\text{19729 桁}) \\
\Ack(4, 3) = 2^{2^{65536}} - 3 \ (\text{「桁数が」19728 桁の数}) \\
\Ack(5, 1) = (\text{もはや指数でもまともに表記できないくらいデカい数})
}
ではそんなアッカーマン関数の定義を見てみましょう。
\Ack(m, n) =
\begin{cases}
n + 1 & (m = 0) \\
\Ack(m - 1, 1) & (m \neq 0, n = 0) \\
\Ack(m - 1, \Ack(m, n - 1)) & (m \neq 0, n \neq 0)
\end{cases}
とてもシンプルな再帰関数ですね。この見かけからは想像しにくいですが、実際に計算してみると前述の通りとてもデカい計算結果が出てきてしまいます。
このアッカーマン関数がとてもデカい数を生み出すことはそれ自体興味深い事実ではありますが、実はアッカーマン関数の真の興味深さは別のところにあります。アッカーマン関数は、原始再帰的でない全域 $\mu$ 再帰関数なのです。
は?(半ギレ)
原始再帰関数とは
数学の世界では「足し算」とか「掛け算」とか「指数関数」とかいろいろな計算が行われますが、それらの計算をごくわずかな部品の組み合わせだけで作れるようにしようぜ、というのが原始再帰関数のアイデアです。原始再帰関数は以下に挙げる三つの関数と二つの作用素だけの組み合わせで関数を記述します。
- 関数(自然数から自然数を作るもの)
- 定数関数
- 後者関数
- 射影関数
- 作用素(関数から関数を作るもの)
- 合成作用素
- 原始再帰作用素
それでは順にみていきましょう。
定数関数
定数関数 $C^k_0$ は $k$ 個の引数を受け取り、それらをすべて無視して自然数 $0$ を返却します。
C^k_0(n_1, \ldots, n_k) = 0
Python で書くとこうなります。
# 数学的な議論とは関係のないところで不必要にプログラムが煩雑になるのを避けるため、
# このプログラムの方では k の指定はなしにしてしまい、
# ただ単に任意長引数を捨てて 0 を返す関数とします。
def C0(*_):
return 0
なお Python での実装は以下で公開しています。これから先この比ではないほど複雑な関数が山のように出てくるので、本当に正しく計算できるのか試してみたいという方は見てみてください。
後者関数
後者関数 $S$ は受け取った自然数の次の自然数を返します。
S(n) = (\text{$n$ の次の数})
def S(n):
return n + 1
射影関数
射影関数 $P^k_i$ は $k$ 個の引数を受け取り、$i$ 番目の引数を返します。
P^k_i(n_1, \ldots, n_k) = n_i
# こちらも定数関数同様 k の指定は省きます。
def P(i):
return lambda *args: args[i - 1]
# Example: P(2)(10, 7, 1) = 7
これで三つの関数は紹介し終えました。次は二つの「作用素」です。作用素は複数の関数を組み合わせて新たな関数を作り出します。
合成作用素
合成作用素 $\circ$ は関数の合成を行います。$k$ 項関数 $f$ と $k$ 個の $l$ 項関数 $g_1, \ldots, g_k$ の合成 $f \circ (g_1, \ldots, g_k)$ を $h$ とすると、$h$ は以下に定められる $l$ 項関数です。
h(n_1, \ldots, n_l) = f(g_1(n_1, \ldots, n_l), \ldots, g_k(n_1, \ldots, n_l))
def composition(f, *gs):
return lambda *args: f(*(g(*args) for g in gs))
受け取った引数 $n_1, \ldots, n_l$ をまず $g_1, \ldots, g_k$ に食わせていき、その各計算結果を $f$ で束ねる的なノリです。形式的定義だとちょっととっつきにくいですが、1 項関数に限定すれば
(f \circ g)(n) = f(g(n))
となり、高校数学なんかでもよく見るやつになりますね。これを引数の数に関して一般化したわけです。
原始再帰作用素
さて最後が原始再帰作用素ですが、これがぶっちぎりで意味不明です。覚悟してください。
原始再帰作用素 $\rho$ は $k$ 項関数 $f$ と $k + 2$ 項関数 $g$ の原始再帰 $\rho(f, g)$ を定めます。$h = \rho(f, g)$ とすると、$h$ は以下に定められる $k + 1$ 項関数です。
\begin{aligned}
h(0, n_1, \ldots, n_k) &= f(n_1, \ldots, n_k) \\
h(S(m), n_1, \ldots, n_k) &= g(m, h(m, n_1, \ldots, n_k), n_1, \ldots, n_k)
\end{aligned}
def primitive_recursion(f, g):
def h(m, *args):
return f(*args) if m == 0 else g(m - 1, h(m - 1, *args), *args)
return h
は?(半ギレ)(2回目)
原始再帰作用素の解釈
$f$ と $g$ の原始再帰 $h = \rho(f, g)$ を実際に手計算してみると以下のような式になることがわかります(文字数が多すぎて見づらくなるのを避けるため、$n_1, \ldots, n_k$ を太字の $\boldsymbol{n}$ で略記します)。
\begin{aligned}
h(m, \boldsymbol{n}) &= g(m - 1, h(m - 1, \boldsymbol{n}), \boldsymbol{n}) \\
&= g(m - 1, g(m - 2, h(m - 2, \boldsymbol{n}), \boldsymbol{n}), \boldsymbol{n}) \\
&= g(m - 1, g(m - 2, g(m - 3, h(m - 3, \boldsymbol{n}), \boldsymbol{n}), \boldsymbol{n}), \boldsymbol{n}) \\
&= \cdots \\
&= g(m - 1, g(m - 2, \ldots g(0, h(0, \boldsymbol{n}), \boldsymbol{n}), \boldsymbol{n}), \ldots, \boldsymbol{n}) \\
&= g(m - 1, g(m - 2, \ldots g(0, f(\boldsymbol{n}), \boldsymbol{n}), \boldsymbol{n}), \ldots, \boldsymbol{n})
\end{aligned}
最後の式を内側から注目してみると、$f$ と $g$ の原始再帰 $\rho(f, g)$ がやっていることは以下のとおりであることが見て取れます。
- $\boldsymbol{n}$ を $f$ に食わせ、$f(\boldsymbol{n})$ を求める。これを $\phi$ とする。
- $\boldsymbol{n}$ と $\phi$ を $g$ に食わせ、$g(0, \phi, \boldsymbol{n})$ を求める。これを $\phi'$ とする。
- $\boldsymbol{n}$ と $\phi'$ を $g$ に食わせ、$g(1, \phi', \boldsymbol{n})$ を求める。これを $\phi''$ とする。
- (以下これを合計 $m$ 回繰り返す)
つまり、関数 $f$ と $g$ の役割は以下のように記述できます。
- $f$ の役割:最初に $\boldsymbol{n}$ を束ね、一つの自然数を求める。
- $g$ の役割:「現在の再帰回数」$m$、「前回の計算結果」$\phi$、「オリジナルの引数」$\boldsymbol{n}$ から「次の計算結果」を求める。
これらを踏まえ Python での実装を書き換えると以下のようになります。
def primitive_recursion(f, g):
def h(recursion_count, *args):
result = f(*args)
for r in range(recursion_count):
result = g(r, result, *args)
return result
return h
このコードにはとても重要な示唆が含まれます。すなわち、原始再帰とは for ループの数学的表現なのです。より具体的に言うと、原始再帰は「いったい何回繰り返し処理を行えばいいのか」が事前に確定している繰り返し処理を記述できます。たとえば $\rho(f, g)(100, \boldsymbol{n})$ などとした場合はきっかり 100 回 $g$ が呼ばれます。
この一方で、「いったい何回繰り返し処理を行えばいいのか」が事前に確定しない繰り返し処理は原始再帰では記述できません。例えば以下のプログラムは原始再帰関数では記述できません。
# 与えられた関数 the_function が 42 を返すような引数を総当たりで見つけ出す
def find42(the_function):
i = 0
while the_function(i) != 42:
i += 1
return i
このようにいつまで処理を繰り返し続ければいいのかわからない関数は原始再帰では記述できません。またどうせ後で説明することになるのでちょっとネタバレしておくと、このような関数は $\mu$ 再帰関数 によって記述されることになります。これについてはまた後で述べます。
補足:射影関数の役割
射影関数ですが、こいつはいったい何のためにあるのか一見するとわかりにくいです。「別になくても何とかなりそうじゃね?」と思えてしまいそうです。
P^k_i(n_1, \ldots, n_k) = n_i
結論から言うと、射影関数は引数の順番を入れ替えるときや引数の一部を抜き出すときなどに必要になります。具体例を見てみましょう。既知の関数 $f$ に対し、こんな関数 $g$ を作りたいとします。
g(m, n) = f(n, m)
$g$ は引数の順番を入れ替えて $f$ に渡すだけの簡単な関数です。と思いきや、今までに紹介した三つの関数と二つの作用素の組み合わせで作るのは意外と難しいです。正解はこうです。
g = f \circ (P^2_2, P^2_1)
この関数に実際に引数 $m, n$ を渡してみましょう。
\begin{aligned}
g(m, n) &= (f \circ (P^2_2, P^2_1))(m, n) \\
&= f(P^2_2(m, n), P^2_1(m, n)) \\
&= f(n, m)
\end{aligned}
このように引数の順番を入れ替えることができます。引数の一部を抜き出すパターンも同様です。こんな関数 $g$ を作るとしましょう。
g(m, n) = f(n)
$g$ は第一引数 $m$ を捨てて第二引数 $n$ のみを $f$ に渡す関数です。「こんな関数いつ必要になるんだよ」とお思いの方もいらっしゃるかもしれませんが、引数の数を調節しなければならない都合上このような関数を定義したくなることも実はままあります。こんな関数 $g$ もやはり射影関数で作れます。
g = f \circ P^2_2
こんなときに射影関数が必要になるわけですね。
原始再帰関数の例
以上に紹介した三つの関数(定数関数、後者関数、射影関数)と二つの作用素(合成作用素、原始再帰作用素)の組み合わせによって記述できる関数を原始再帰関数といいます。いくつか具体例を見ていきましょう。
1 を返す定数関数
C^k_1 = S \circ C^k_0
この関数は $k$ 個の引数を受け取り、それらをすべて無視して自然数 $1$ を返却します。あとは同じノリで $2$ を返す定数関数 $C^k_2$ とか $3$ を返す定数関数 $C^k_3$ も作れます。
2 を足す関数
\operatorname{plus2} = S \circ S
この関数は自然数 $n$ を受け取り、それに $2$ を足した数を返却します。
足し算
\add = \rho(P^1_1, S \circ P^3_2)
この記事の本題からはそれてしまうのでなぜこの式で和が求まるのかの厳密な説明は割愛しますが、ざっくり説明すると引数 $m, n$ に対し原始再帰作用素を使って「$n$ に $S$ を $m$ 回繰り返し適用する」という処理を実現しています。これにより $m + n$ が求まるわけです。
2 倍する関数
\double = \add \circ (P^1_1, P^1_1)
受け取った引数を二つ $\add$ へ渡すことで 2 倍できます。
掛け算
\multiply = \rho(C^1_0, \add \circ (P^3_2, P^3_3))
これも足し算と同様、引数 $m$, $n$ に対し「$0$ に $n$ を $m$ 回足す」という操作を行い $mn$ を計算しています。
冪乗
\exponentiate = \rho(C^1_1, \multiply \circ (P^3_2, P^3_3)) \circ (P^2_2, P^2_1)
ここは先ほど説明した射影関数のトリックを使っています。まず「第二引数の第一引数乗を求める関数」を原始再帰作用素で定義し、そのあと射影関数を用いて引数の順序を入れ替えることで「第一引数の第二引数乗を求める関数」を作っています。「0 の 0 乗」とか未定義の部分に関しては見なかったことにします
前者関数
\predecessorOf = \rho(C^0_0, P^2_1)
この関数は自然数 $n$ を受け取り、$n$ の一つ前の自然数を返却します(ただし $\predecessorOf(0)$ は便宜的に $0$ であるとします)。
切り詰め減算
\subtract = \rho(P^1_1, \predecessorOf \circ P^3_2) \circ (P^2_2, P^2_1)
この関数は自然数 $m, n$ を受け取り、$\max(m - n, 0)$ を返却します(つまり実際の減算結果が負になってしまう場合は便宜的に $0$ を返すというわけです)。
また、原始再帰関数は Boolean 値を返す関数も疑似的に作ることができてしまいます。与えられた引数が所与の条件を満たすならば $1$ を、そうでないなら $0$ を返却するとすればよいのです。つまり C 言語と似た感じのノリですね。
ゼロ判定
\isZero = \rho(C^0_1, C^2_0)
この関数は与えられた自然数が $0$ ならば $1$ を、そうでないなら $0$ を返却します。
小なりイコール・大なりイコール
$m \leq n$ は、$m$ と $n$ の切り詰め減算 $\subtract(m, n) = \max(m - n, 0)$ が $0$ であることと同値です。よってこのように定義されます。
\isLessThanOrEqualTo = \isZero \circ \subtract
また $m \geq n$ は言うまでもなく $n \leq m$ と同値なので、いま定義した小なりイコールの引数の順番をひっくり返してやれば大なりイコールが定義されます。
\isGreaterThanOrEqualTo = \isLessThanOrEqualTo \circ (P^2_2, P^2_1)
条件分岐
以上に例を挙げた Boolean 値を返す関数を使って条件分岐を実装することすらできます。
\ifThenElse = \rho(P^2_2, P^4_3)
この関数は第一引数が $0$ ならば第三引数を、そうでないなら第二引数を返します。つまりこういうことです。
\ifThenElse(c, m, n) =
\begin{cases}
m & (c \neq 0) \\
n & (c = 0)
\end{cases}
Excel の IF 関数と一緒ですね。
論理演算
ここまでくればもはや驚かないでしょうが、AND, OR, NOT 等の論理演算も原始再帰関数で定義できます。
\displaylines {
\and = \ifThenElse \circ (P^2_1, P^2_2, C^2_0) \\
\or = \ifThenElse \circ (P^2_1, C^2_1, P^2_2) \\
\myNot = \ifThenElse \circ (P^1_1, C^1_0, C^1_1)
}
イコール・小なり・大なり
するとイコール・小なり・大なりもこのように定義されるわけです。
\displaylines {
\isEqualTo = \and \circ (\isLessThanOrEqualTo, \isGreaterThanOrEqualTo) \\
\isLessThan = \myNot \circ \isGreaterThanOrEqualTo \\
\isGreaterThan = \myNot \circ \isLessThanOrEqualTo
}
剰余演算
さらに剰余演算も定義できます。$m$ を $n$ で割った剰余を $\remainderOf(m, n)$ とすると以下の関係式が成立します。$0$ で割ったあまりとかはここでも見なかったことにします(小声)
\begin{aligned}
\remainderOf(0, n) &= 0 \\
\remainderOf(S(m), n) &=
\begin{cases}
0 & (S(\remainderOf(m, n)) = n) \\
S(\remainderOf(m, n)) & (\mathrm{otherwise})
\end{cases}
\end{aligned}
これを原始再帰作用素を用いてうまいこと記述すると以下のようになります。
\remainderOf = \rho \left(
\begin{gathered}
C^1_0, \\
\ifThenElse \circ \left(
\begin{gathered}
\isEqualTo \circ \left(
\begin{gathered}
S \circ P^3_2, \\
P^3_3
\end{gathered}
\right), \\
C^3_0, \\
S \circ P^3_2
\end{gathered}
\right)
\end{gathered}
\right)
整除可能性(割り切れるかどうか)
$m$ が $n$ で割り切れるとは $m$ を $n$ で割ったあまりが $0$ であるということですから、以下のように簡単に書けます。
\isDivisibleBy = \isZero \circ \remainderOf
切り捨て除算
ついでに割り算も定義しておきます。$m$ を $n$ で割った商 $\divide(m, n)$ は以下の関係式を満たします。
\begin{aligned}
\divide(0, n) &= 0 \\
\divide(S(m), n) &=
\begin{cases}
S(\divide(m, n)) & (S(\remainderOf(m, n)) = n) \\
\divide(m, n) & (\mathrm{otherwise})
\end{cases}
\end{aligned}
これも原始再帰作用素で書くとこうなります。
\divide = \rho \left(
\begin{gathered}
C^1_0, \\
\ifThenElse \circ \left(
\begin{gathered}
\isEqualTo \circ \left(
\begin{gathered}
S \circ \remainderOf \circ \left(
\begin{gathered}
P^3_1, \\
P^3_3
\end{gathered}
\right), \\
P^3_3
\end{gathered}
\right), \\
S \circ P^3_2, \\
P^3_2
\end{gathered}
\right)
\end{gathered}
\right)
切り捨て冪根
さらについでに冪根も定義しておきます。$m$ の $n$ 乗根の切り捨て $\nthRootOf(m, n)$ は以下の関係式を満たします。0 乗根に関してはやはり見なかったことにします。
\begin{aligned}
\nthRootOf(0, n) &= 0 \\
\nthRootOf(S(m), n) &=
\begin{cases}
S(\nthRootOf(m, n)) & (S(\nthRootOf(m, n))^n \le S(m)) \\
\nthRootOf(m, n) & (\mathrm{otherwise})
\end{cases}
\end{aligned}
というわけでこうなります。
\nthRootOf = \rho \left(
\begin{gathered}
C^1_0, \\
\ifThenElse \circ \left(
\begin{gathered}
\isLessThanOrEqualTo \circ \left(
\begin{gathered}
\exponentiate \circ \left(
\begin{gathered}
S \circ P^3_2, \\
P^3_3
\end{gathered}
\right), \\
S \circ P^3_1
\end{gathered}
\right), \\
S \circ P^3_2, \\
P^3_2
\end{gathered}
\right)
\end{gathered}
\right)
第二引数を固定してやれば平方根や立方根を求める関数も作れます。
\displaylines {
\squareRootOf = \nthRootOf \circ (P^1_1, C^1_2) \\
\cubicRootOf = \nthRootOf \circ (P^1_1, C^1_3)
}
原始再帰関数の限界
さて以上に見たように、原始再帰関数という計算システムは for 文と if 文を表現できます。これだけあれば大概の計算は表現できますし、むしろ原始再帰関数で表現できない計算を思いつくことの方が難しいでしょう。
しかしながら、過去においてはこの原始再帰関数があらゆる計算を表せるのか否かということは未解決の問題でした。つまり、どんな関数も原始再帰関数で表すことができるのか、あるいはそうでないのかは、誰も証明も反証もできていなかったのです。
そんな中ヴィルヘルム・アッカーマンにより考案されたのがアッカーマン関数です。アッカーマンは自身の考案したアッカーマン関数が原始再帰関数では表現できないことを証明してしまいました。したがって、あらゆる計算は原始再帰関数で表現できるという淡い期待はもろくも打ち砕かれることとなってしまいました。
アッカーマン関数の非原始再帰性の証明
準備
アッカーマン関数の非原始再帰性の証明に入る前に、証明に使うためのアッカーマン関数の簡単な性質の確認をしておきます。ただ性質の証明の部分は記事の本題とは関係ないので、証明は畳んでおきます。興味のある人だけ読んでください。
性質 1: $\Ack(1, n) = n + 2$
証明
$n = 0$ のとき、
\begin{aligned}
\Ack(1, 0) &= \Ack(0, 1) \\
& = 2
\end{aligned}
よって $n = 0$ に関して与命題は成立する。次にとある $n'$ が存在して $\Ack(1, n') = n' + 2$ と仮定すると、
\begin{aligned}
\Ack(1, n' + 1) &= \Ack(0, \Ack(1, n')) \\
&= \Ack(0, n' + 2) && (\because \text{仮定より}) \\
&= n' + 3 \\
&= (n' + 1) + 2
\end{aligned}
よって帰納的に任意の $n$ に対し与命題は真である。(証明終)
性質 2: $\Ack(2, n) = 2n + 3$
証明
$n = 0$ のとき、
\begin{aligned}
\Ack(2, 0) &= \Ack(1, 1) \\
&= 3 && (\because \text{性質 1})
\end{aligned}
よって $n = 0$ に関して与命題は成立する。次にとある $n'$ が存在して $\Ack(2, n') = 2n' + 3$ と仮定すると、
\begin{aligned}
\Ack(2, n' + 1) &= \Ack(1, \Ack(2, n')) \\
&= \Ack(1, 2n' + 3) && (\because \text{仮定より}) \\
&= 2n' + 5 && (\because \text{性質 1}) \\
&= 2(n' + 1) + 3
\end{aligned}
よって帰納的に任意の $n$ に対し与命題は真である。(証明終)
性質 3: $n < \Ack(m, n)$
証明
$m = 0$ のとき、
n < \Ack(0, n) = n + 1
よって $m = 0$ に関して与命題は成立する。また
\begin{aligned}
\Ack(m + 1, n) &= \Ack(m, \Ack(m + 1, n - 1)) \\
&= \Ack(m, \Ack(m, \Ack(m + 1, n - 2))) \\
&= \cdots \\
&= \underbrace{\Ack(m, \Ack(m, \cdots \Ack(m + 1, 0)))}_{\text{$n + 1$ $\Ack(\cdot)$s}} \\
&= \underbrace{\Ack(m, \Ack(m, \cdots \Ack(m, 1)))}_{\text{$n + 1$ $\Ack(\cdot)$s}}
\end{aligned}
である。ここでとある $m'$ が存在して $n < \Ack(m', n)$ と仮定すると、
\begin{aligned}
1 &< \Ack(m', 1) \\
&< \Ack(m', \Ack(m', 1)) \\
&< \Ack(m', \Ack(m', \Ack(m', 1))) \\
&< \cdots \\
&< \underbrace{\Ack(m', \Ack(m', \cdots \Ack(m', 1)))}_{\text{$n + 1$ $\Ack(\cdot)$s}} \\
&= \Ack(m' + 1, n)
\end{aligned}
したがって、
\Ack(m' + 1, n) > n + 1 > n
よって帰納的に任意の $m$ と $n$ に対し与命題は真である。(証明終)
性質 4: $\Ack(m, n) < \Ack(m, n + 1)$
証明
$m = 0$ のとき、
\Ack(0, n) = n + 1 < n + 2 = \Ack(0, n + 1)
よって $m = 0$ に関して与命題は成立する。また
\begin{aligned}
\Ack(m + 1, n) &< \Ack(m, \Ack(m + 1, n)) && (\because \text{性質 3}) \\
&= \Ack(m + 1, n + 1)
\end{aligned}
よって与命題は正の $m$ に関しても真であるので、任意の $m$ と $n$ に対し真である。(証明終)
性質 5: $\Ack(m, n + 1) \leq \Ack(m + 1, n)$
証明
$n = 0$ のとき、
\Ack(m, 1) = \Ack(m + 1, 0)
よって $n = 0$ に関して与命題は成立する。
ここでとある $n'$ について $\Ack(m, n' + 1) \leq \Ack(m + 1, n')$ が成り立つと仮定する。まず性質 3 より $n' + 2 \leq \Ack(m, n' + 1)$ であることと性質 4 を組み合わせて $\Ack(m, n' + 2) \leq \Ack(m, \Ack(m, n' + 1))$ が成り立つので、
\begin{aligned}
\Ack(m, n' + 2) &\leq \Ack(m, \Ack(m, n' + 1)) \\
&\leq \Ack(m, \Ack(m + 1, n')) && (\because \text{仮定と性質 4}) \\
&= \Ack(m + 1, n' + 1)
\end{aligned}
よって帰納的に任意の $n$ と $m$ に対し与命題は真である。(証明終)
性質 6: $\Ack(m, n) < \Ack(m + 1, n)$
証明
\begin{aligned}
\Ack(m, n) &< \Ack(m, n + 1) && (\because \text{性質 4}) \\
&\leq \Ack(m + 1, n) && (\because \text{性質 5})
\end{aligned}
(証明終)
性質 7: $\Ack(l, \Ack(m, n)) < \Ack(l + m + 2, n)$
証明
\begin{aligned}
\Ack(l, \Ack(m, n)) &\leq \Ack(l + m, \Ack(m, n)) && (\because \text{性質 6}) \\
&< \Ack(l + m, \Ack(l + m + 1, n)) && (\because \text{性質 4, 6}) \\
&= \Ack(l + m + 1, n + 1) \\
&\leq \Ack(l + m + 2, n) && (\because \text{性質 5})
\end{aligned}
(証明終)
証明
さて満を持してアッカーマン関数の非原始再帰性の証明に入ります。記事冒頭でご紹介したようにアッカーマン関数は超巨大な自然数を生み出してしまいますが、これがアッカーマン関数の非原始再帰性の証明に繋がります。ざっくり説明すると、アッカーマン関数がいかなる原始再帰関数よりもデカい自然数を生み出してしまうことを示すのです。そのようにしてアッカーマン関数が原始再帰関数では表現できないことを証明できます。
まず、以下が成り立つことを「アッカーマン関数は関数 $f$ よりつよい」と呼ぶことにします。
とある自然数 $m$ が存在し、任意の引数 $\boldsymbol{n}$ に対し
f(\boldsymbol{n}) < \Ack(m, \max(\boldsymbol{n}))
が成り立つこと。
このとき、アッカーマン関数がいかなる原始再帰関数よりもつよいことを示せばアッカーマン関数が原始再帰関数では表現できないことを証明したことになります。なぜでしょうか?
もし仮にアッカーマン関数が任意の原始再帰関数よりもつよく、なおかつアッカーマン関数自身もまた原始再帰関数であったと仮定します。するとアッカーマン関数はアッカーマン関数自身よりもつよいことになりますから、とある自然数 $l$ が存在して任意の自然数 $m, n$ に対し
\Ack(m, n) < \Ack(l, \max(m, n))
だということになってしまいますが、これは明らかに成り立ちません。例えば $m = l + 1, n = l + 2$ とすれば、
\displaylines {
\Ack(m, n) = \Ack(l + 1, l + 2) \\
\Ack(l, \max(m, n)) = \Ack(l, l + 2)
}
となり、性質 6 より前者の方が後者より大きいからです。よって、アッカーマン関数が任意の原始再帰関数よりつよいことを示せばアッカーマン関数の非原始再帰性を示せることになります。それでは証明していきましょう。
補題 1: アッカーマン関数は定数関数 $C^k_0$ よりつよい。
証明
$k$ 個の任意の引数 $\boldsymbol{n} = n_1, \ldots, n_k$ に対し、
C^k_0(\boldsymbol{n}) = 0 < \max(\boldsymbol{n}) + 1 = \Ack(0, \max(\boldsymbol{n}))
であるため。(証明終)
補題 2: アッカーマン関数は後者関数 $S$ よりつよい。
証明
任意の自然数 $n$ に対し、
\begin{aligned}
S(n) &= n + 1 \\
&< n + 2 \\
&= \Ack(1, \max(n)) && (\because \text{性質 1})
\end{aligned}
であるため。(証明終)
(ここにおける $n$ は太字の $\boldsymbol{n}$ のような引数列ではなくただの自然数であるため $\max(n) = n$ であることに注意してください)
補題 3: アッカーマン関数は射影関数 $P^k_i$ よりつよい。
証明
$k$ 個の任意の引数 $\boldsymbol{n} = n_1, \ldots, n_k$ に対し、
P^k_i(\boldsymbol{n}) = n_i < \max(\boldsymbol{n}) + 1 = \Ack(0, \max(\boldsymbol{n}))
であるため。(証明終)
補題 4: アッカーマン関数が関数 $f$ と $g_1, \ldots, g_k$ のいずれよりもつよいならば、アッカーマン関数はこれらの合成 $f \circ (g_1, \ldots, g_k)$ よりもつよい。
証明
アッカーマン関数が $f$ と $g_1, \ldots, g_k$ のいずれよりもつよいという前提条件より、
\begin{aligned}
f(\boldsymbol{p}) &< \Ack(m, \max(\boldsymbol{p})) \\
g_1(\boldsymbol{q}) &< \Ack(n_1, \max(\boldsymbol{q})) \\
&\vdots \\
g_k(\boldsymbol{q}) &< \Ack(n_k, \max(\boldsymbol{q}))
\end{aligned}
を満たす $m, n_1, \ldots, n_k$ が $\boldsymbol{p}, \boldsymbol{q}$ にかかわらず常に存在する。
ここで $g_1(\boldsymbol{q}), \ldots, g_k(\boldsymbol{q})$ の中で最も大きいものが $g_j(\boldsymbol{q})$ であるとすると、
\begin{aligned}
f \circ (g_1, \ldots, g_k)(\boldsymbol{q}) &= f(g_1(\boldsymbol{q}), \ldots, g_k(\boldsymbol{q})) \\
&< \Ack(m, \max\{g_1(\boldsymbol{q}), \ldots, g_k(\boldsymbol{q})\}) \\
&= \Ack(m, g_j(\boldsymbol{q})) \\
&< \Ack(m, \Ack(n_j, \max(\boldsymbol{q}))) && (\because \text{性質 4}) \\
&< \Ack(m + n_j + 2, \max(\boldsymbol{q})) && (\because \text{性質 7})
\end{aligned}
である。(証明終)
補題 5: アッカーマン関数が関数 $f$ と $g$ のいずれよりもつよいならば、アッカーマン関数はこれらの原始再帰 $\rho(f, g)$ よりもつよい。
証明
アッカーマン関数が $f$ と $g$ のいずれよりもつよいという前提条件より、
\begin{aligned}
f(\boldsymbol{r}) &< \Ack(m, \max(\boldsymbol{r})) \\
g(p, q, \boldsymbol{r}) &< \Ack(n, \max(p, q, \boldsymbol{r}))
\end{aligned}
を満たす $m, n$ が $p, q, \boldsymbol{r}$ にかかわらず常に存在する。
次に $h = \rho(f, g)$ とし、以下の補題を証明する。
補題 5-1:
とある自然数 $s$ が存在し、任意の自然数 $t$ と引数 $\boldsymbol{u}$ に対し
h(t, \boldsymbol{u}) < \Ack(s, t + \max(\boldsymbol{u}))
が成り立つ。
証明: $t = 0$ のとき、
h(0, \boldsymbol{u}) = f(\boldsymbol{u}) < \Ack(m, 0 + \max(\boldsymbol{u}))
よって $t = 0$ に関して与命題は成立する。ここでとある $t'$ と $s'$ が存在し $h(t', \boldsymbol{u}) < \Ack(s', t' + \max(\boldsymbol{u}))$ であることを仮定すると、
\begin{aligned}
h(t' + 1, \boldsymbol{u}) &= g(t', h(t', \boldsymbol{u}), \boldsymbol{u}) \\
&< \Ack(n, \max(t', h(t', \boldsymbol{u}), \boldsymbol{u}))
\end{aligned}
が成り立ち、加えて
\begin{aligned}
&t' \leq t'+\max(\boldsymbol{u}) < \Ack(s', t' + \max(\boldsymbol{u})) && (\because \text{性質 3}) \\
&h(t', \boldsymbol{u}) < \Ack(s', t' + \max(\boldsymbol{u})) && (\because \text{仮定より}) \\
&\max(\boldsymbol{u}) \leq t'+\max(\boldsymbol{u}) < \Ack(s', t' + \max(\boldsymbol{u})) && (\because \text{性質 3})
\end{aligned}
なので、$\max(t', h(t', \boldsymbol{u}), \boldsymbol{u}) < \Ack(s', t' + \max(\boldsymbol{u}))$ である。したがって
\begin{aligned}
h(t' + 1, \boldsymbol{u}) &< \Ack(n, \max(t', h(t', \boldsymbol{u}), \boldsymbol{u})) \\
&< \Ack(n, \Ack(s', t' + \max(\boldsymbol{u}))) && (\because \text{性質 4}) \\
&< \Ack(n + s' + 2, t' + \max(\boldsymbol{u})) && (\because \text{性質 7}) \\
&< \Ack(n + s' + 2, (t' + 1) + \max(\boldsymbol{u})) && (\because \text{性質 4})
\end{aligned}
よって帰納的に任意の $p$ に対し与命題は真である。(証明終)
補題 5-1 よりとある自然数 $s$ が存在し、任意の $t$ と $\boldsymbol{u}$ に対し以下が成り立つ。
\begin{aligned}
h(t, \boldsymbol{u}) &< \Ack(s, t + \max(\boldsymbol{u})) \\
&\leq \Ack(s, 2 \times \max(t, \boldsymbol{u})) && (\because \text{性質 4}) \\
&< \Ack(s, 2 \times \max(t, \boldsymbol{u}) + 3) && (\because \text{性質 4}) \\
&= \Ack(s, \Ack(2, \max(t, \boldsymbol{u}))) && (\because \text{性質 2}) \\
&< \Ack(s + 4, \max(t, \boldsymbol{u})) && (\because \text{性質 7})
\end{aligned}
よってアッカーマン関数は $h = \rho(f, g)$ よりもつよい。(証明終)
したがってアッカーマン関数は原始再帰関数を形作る三つの関数と二つの作用素をいかに組み合わせた関数よりもつよいので、アッカーマン関数はいかなる原始再帰関数よりもつよいと証明できました。すなわちアッカーマン関数は原始再帰関数では表現できません。
μ 再帰関数
アッカーマン関数は原始再帰関数では表現できませんでした。つまり残念ながら原始再帰関数はあらゆる計算を表せる仕組みではなかったわけです。
しかし、実はアッカーマン関数は $\mu$ 再帰関数という仕組みでは表せることが分かっています。$\mu$ 再帰関数は以下の関数と作用素からなります。
- 定数関数 $C^k_0$
- 後者関数 $S$
- 射影関数 $P^k_i$
- 合成作用素 $\circ$
- 原始再帰作用素 $\rho$
- 最小化作用素 $\mu$
つまり $\mu$ 再帰関数は原始再帰関数に「最小化作用素 $\mu$」なるものを付け加えた仕組みです。$k + 1$ 項関数 $f$ に対し $\mu(f)$ を $g$ と置くと、$g$ は以下を満たす $k$ 項関数です。
g(\boldsymbol{n}) := (\text{$f(m, \boldsymbol{n}) = 0$ を満たす最小の $m$})
def mu(f):
def g(*args):
i = 0
while f(i, *args) != 0:
i += 1
return i
return g
いままでの作用素と比べるとなにやら様子がおかしいです。実際、最小化作用素にはある重大な問題点があります。
μ 再帰関数の問題点
少し前に原始再帰関数をいくつか例示しましたが、その中にこんなのがありました。
C^k_1 = S \circ C^k_0
受け取った $k$ 個の引数をすべて捨てて $1$ を返す定数関数です。ここで $\mu(C^k_1)$ について考えてみましょう。
\mu(C^k_1)(\boldsymbol{n}) = (\text{$C^k_1(m, \boldsymbol{n}) = 0$ を満たす最小の $m$})
$\mu(C^k_1)$ は以上のような関数になるわけですが、しかし $C^k_1$ はどんな引数に対しても必ず $1$ を返す関数です。したがって「$C^k_1(m, \boldsymbol{n}) = 0$ を満たす最小の $m$」など存在しません。ここに最小化作用素の、ひいては $\mu$ 再帰関数の問題点が現れています。$\mu$ 再帰関数は原始再帰関数とは違って返り値が定義されない場合があるのです。
別の例も見てみましょう。
\mu(\isGreaterThanOrEqualTo)(n) =
\begin{cases}
\mathrm{undefined} & (n = 0) \\
0 & (n \neq 0)
\end{cases}
この関数は引数が $0$ のときのみ返り値が未定義です。このように一部の引数に対してのみ返り値が定義されないパターンもあるわけです。
さらに実は最小化作用素にはもっと大きな問題もあります。ここになにか 2 項原始再帰関数 $f$ があるとしましょう。あなたは $\mu(f)(5)$ の値を求めようとしているとします。つまりあなたが知りたいのは「$f(m, 5) = 0$ を満たす最小の $m$」です。この $m$ を具体的にどうやって求めるのかというのが問題なのです。
最も簡単な方法は $m = 0$ から順番に確かめていくことでしょう。しかしこの方法だと、例えば $m = 5000000000000000$ で初めて $f(m, 5) = 0$ になるときなど 5000 兆回も計算を行わなければならないことになります。
いや、5000 兆回で済むならまだマシな方です。先ほど見た $\mu(C^k_1)$ のようにそもそも返り値が未定義である(すなわち存在しない)場合などは 5000 京回やっても 5000 垓回やっても答えが求まらないことになりますし、もっと悪いことに「そもそも返り値など存在していない」、すなわち「いくら計算を行ったところで条件を満たす $m$ が見つかることなど決してない」ということはあなたにはわかりません。すなわち、辛抱強く計算を続ければいつかは答えが見つかるのか、それとももういくら計算しても無駄なのか、それがわからないままいつまでも計算し続けなければならないのです。
この問題をどうにかすることはできないのでしょうか?すなわち、$\mu(f)(\boldsymbol{n})$ の値を効率的に求めたり、そもそもそれ以前に $\mu(f)(\boldsymbol{n})$ は存在するのか、それを知る方法はないのでしょうか?
・・・・・・結論から言うと、そのような方法はないです。まだそのような方法が考案されていないとかそういう話ではなく、そもそも $\mu(f)(\boldsymbol{n})$ が存在するか判定する方法は存在しないことが証明されているのです。
先ほど「原始再帰作用素は for 文に対応している」という話をしましたが、これになぞらえると最小化作用素の方は while 文に対応していることになります。すなわち、原始再帰作用素は繰り返し回数が事前に確定している(ゆえにいつかは終わることが確定している)繰り返し処理に相当し、最小化作用素の方は繰り返し回数が確定していない(ゆえにいつか終わるとは限らない)繰り返し処理に相当すると言えます。まあ C 言語なんかだと for 文を while 文の代わりに使えるのでこの比喩は必ずしも成り立たないんですけどね
全域 μ 再帰関数
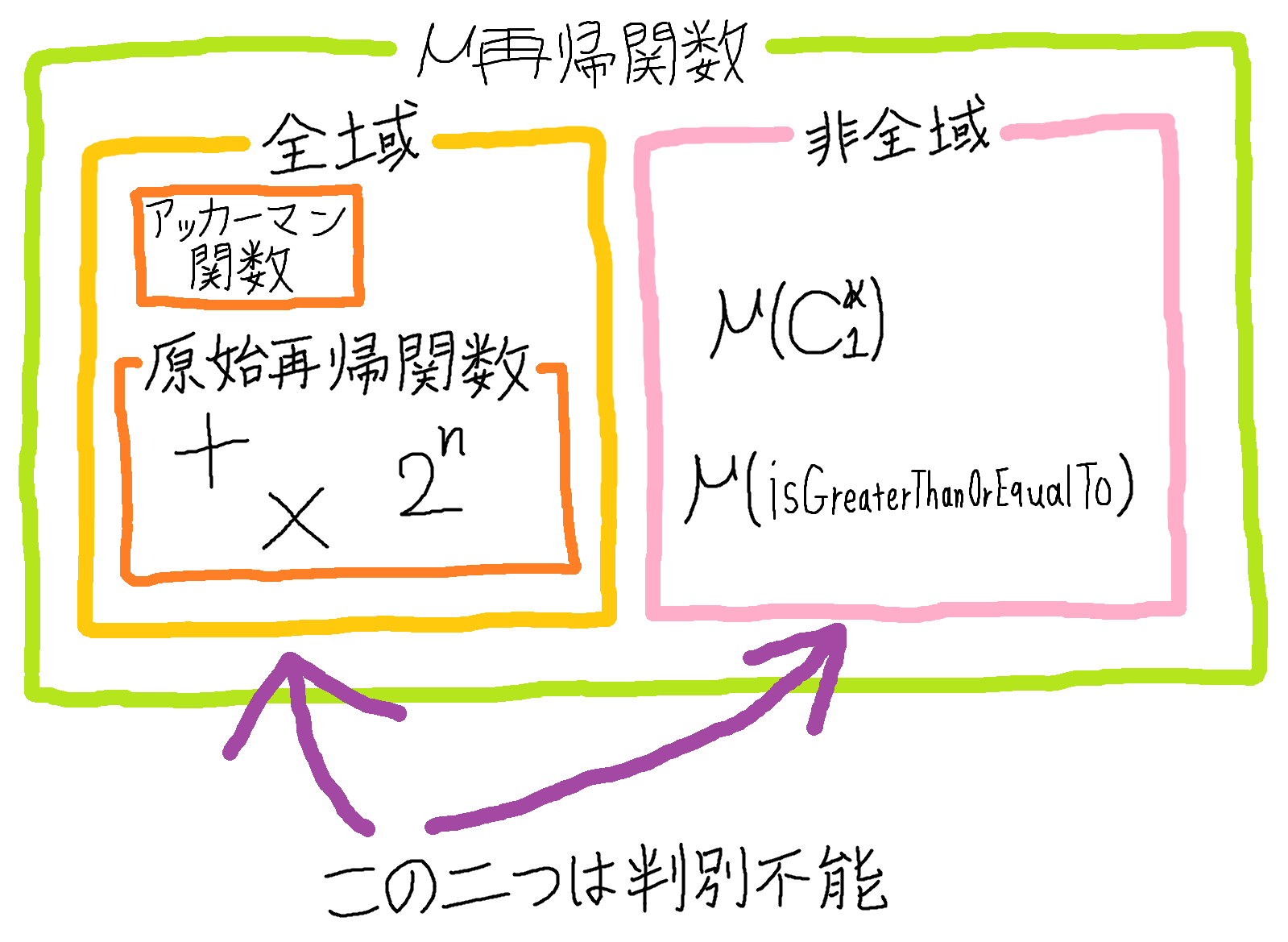
なんか微妙な結論になってしまいましたが、ご安心ください。先ほどアッカーマン関数は $\mu$ 再帰関数でなければ表現できないと言いましたが、少なくともアッカーマン関数はあらゆる引数の組み合わせに対し返り値が定義されています(つまり最小化作用素による探索は必ず有限回で終了します)。そのような $\mu$ 再帰関数を全域 $\mu$ 再帰関数といいます。また原始再帰関数は当然すべて全域 $\mu$ 再帰関数です。
いままでに分かったことを図にまとめるとこのようになります。
というわけでアッカーマン関数が全域 $\mu$ 再帰関数であることを確認しましょう。要するに以下の二つを確認すればよいです。
- アッカーマン関数の返り値があらゆる引数の組み合わせに対し定義されていること
- アッカーマン関数が $\mu$ 再帰関数であること
アッカーマン関数の全域性の証明
いままでアッカーマン関数の返り値が任意の引数に対し定義されていることは自明の事実としてスルーしていましたが、本当なら真っ先に証明しておくべき重要事項でした。二重の入れ子になった帰納法になるのでちょっとややこしいですが、落ち着いて見てみれば結構簡単に証明できます。
証明
$m = 0$ のとき、
\Ack(0, n) = n + 1
よって任意の $n$ に対し $(0, n)$ がアッカーマン関数の定義域に含まれることは自明。
ここでとある $m'$ が存在して任意の $n$ に対し $(m', n)$ がアッカーマン関数の定義域に含まれると仮定すると、$\Ack(m', 1) = \Ack(m' + 1, 0)$ より $(m' + 1, 0)$ もアッカーマン関数の定義域に含まれる。
次にとある $n'$ が存在して $(m' + 1, n')$ がアッカーマン関数の定義域に含まれると仮定すると、$\Ack(m', \Ack(m' + 1, n')) = \Ack(m' + 1, n' + 1)$ より $(m' + 1, n' + 1)$ もアッカーマン関数の定義域に含まれる。よって帰納的に任意の $n$ に対し $(m' + 1, n)$ はアッカーマン関数の定義域に含まれる。
よって帰納的に任意の $(m, n)$ はアッカーマン関数の定義域に含まれる。(証明終)
アッカーマン関数の μ 再帰性の証明
次に原始再帰関数では表せなかったアッカーマン関数が $\mu$ 再帰関数では表せることを証明します。しかしその前にいくつか下準備をします。
下準備 0: もろもろの関数の用意
限定的最小化作用素
これまで見てきたとおり原始再帰関数は三つの関数と二つの作用素の組み合わせでできるわけですが、ここで後々のために作用素を一つ勝手に付け加えます。その作用素を限定的最小化作用素 $\beta$ と呼ぶことにします($\beta$ は "bounded" の頭文字をとりました)。$k$ 項関数 $b$ と $k + 1$ 項関数 $f$ に対し $\beta(b, f)$ を $g$ と置くと、$g$ は以下を満たす $k$ 項関数です。
g(\boldsymbol{n}) = (\text{$f(m, \boldsymbol{n}) = 0$ を満たす $m$ が $0 \leq m < b(\boldsymbol{n})$ の範囲に存在するならばそのうち最小のもの, しないなら $b(\boldsymbol{n})$})
要は最小化作用素の探索範囲を $b(\boldsymbol{n})$ を上限とする有限の範囲に限定したものです。これがあると後で便利なのですが、しかし勝手に作用素を付け加えるというのも横暴な話です。なのでこれから「$b$ と $f$ が原始再帰的ならば $\beta(b, f)$ も原始再帰的である」ことを証明します。もしこれが証明できれば原始再帰関数の枠組みの中に限定的最小化作用素があろうがなかろうが結局差異はないということになるので、安心して限定的最小化作用素を追加することができます。それでは張り切って証明していきましょう。
証明
所与の $k + 1$ 項原始再帰関数 $f$ に対し、$k + 1$ 項関数 $g'$ を以下の如く定める。
\begin{aligned}
g'(0, \boldsymbol{n}) &= 0 \\
g'(S(m), \boldsymbol{n}) &=
\begin{cases}
g'(m, \boldsymbol{n}) & (g'(m, \boldsymbol{n}) < m) \\
m & (g'(m, \boldsymbol{n}) = m \land f(m, \boldsymbol{n}) = 0) \\
S(m) & (\mathrm{otherwise})
\end{cases}
\end{aligned}
このとき、$g'(m, \boldsymbol{n})$ は「$f(m', \boldsymbol{n}) = 0$ を満たす $m'$ が $0 \le m' < m$ の範囲に存在するならばそのうち最小のもの、しないなら $m$」になっている。このことは帰納法により容易に確かめられる。$m = 0$ の場合は自明だし、$m = m'$ で成り立つという仮定の下 $m = S(m')$ でも成り立つことは $g'$ の定義式より明らかである。したがって $\beta(b, f)(\boldsymbol{n}) = g'(b(\boldsymbol{n}), \boldsymbol{n})$ が成り立つので、$g'$ が原始再帰的ならば $\beta(b, f)$ も明らかに原始再帰的である。
ここで $g'$ の定義式は以下のようにも記述できる。
\begin{aligned}
g'(0, \boldsymbol{n}) &= C^k_0(\boldsymbol{n}) \\
g'(S(m), \boldsymbol{n}) &= \ifThenElse\left(
\begin{aligned}
\begin{gathered}
\isLessThan(g'(m, \boldsymbol{n}), m), \\
g'(m, \boldsymbol{n}), \\
\ifThenElse\left(
\begin{aligned}
\begin{gathered}
\and\left(
\begin{aligned}
\begin{gathered}
\isEqualTo(g'(m, \boldsymbol{n}), m), \\
\isZero(f(m, \boldsymbol{n}))
\end{gathered}
\end{aligned}
\right), \\
m, \\
S(m)
\end{gathered}
\end{aligned}
\right)
\end{gathered}
\end{aligned}
\right)
\end{aligned}
さらに $k + 2$ 項関数 $g''$ を以下の如く定める。
\displaylines{
g''(m, x, \boldsymbol{n}) = \ifThenElse\left(
\begin{aligned}
\begin{gathered}
\isLessThan(x, m), \\
x, \\
\ifThenElse\left(
\begin{aligned}
\begin{gathered}
\and\left(
\begin{aligned}
\begin{gathered}
\isEqualTo(x, m), \\
\isZero(f(m, \boldsymbol{n}))
\end{gathered}
\end{aligned}
\right), \\
m, \\
S(m)
\end{gathered}
\end{aligned}
\right)
\end{gathered}
\end{aligned}
\right) \\
(\therefore g'(S(m), \boldsymbol{n}) = g''(m, g'(m, \boldsymbol{n}), \boldsymbol{n}))
}
このとき $g' = \rho(C^k_0, g'')$ であることは原始再帰作用素の定義より明らかである。また前提条件より $f$ と $b$ は原始再帰的であり、したがって $g''$ も原始再帰的であり、したがって $g'$ も原始再帰的である。よって(前述の通り)$\beta(b, f)$ は原始再帰的である。(証明終)
さらに追加
いま定義した限定的最小化作用素を用い、こんな作用素も作ってみましょう。
- 限定的全称量化作用素 $\forAll$
- $0$ 以上 $b(\boldsymbol{n})$ 未満の任意の自然数 $m$ に対し $f(m, \boldsymbol{n}) \neq 0$ ならば $\forAll(b, f)(\boldsymbol{n}) = 1$, そうでないなら $0$
- 限定的存在量化作用素 $\forAny$
- $0$ 以上 $b(\boldsymbol{n})$ 未満のとある自然数 $m$ に対し $f(m, \boldsymbol{n}) \neq 0$ ならば $\forAny(b, f)(\boldsymbol{n}) = 1$, そうでないなら $0$
要は数理論理学でいうところの $\forall$ と $\exists$ ですね。限定的最小化作用素を使えば簡単に定義できちゃいます。
\displaylines {
\forAll(b, f) = \isEqualTo \circ (\beta(b, f), b) \\
\forAny(b, f) = \myNot \circ \isEqualTo \circ (\beta(b, \myNot \circ f), b)
}
素数判定関数
この最小化作用素を用いて素数判定関数を定義できます。自然数 $n$ が素数である必要十分条件は、
- $n$ が $2$ 以上である
- $2$ 以上 $\sqrt{n}$ 以下の自然数に $n$ の約数が存在しない
- 強引に言い換えれば、$0$ 以上 $\lfloor \sqrt{n} \rfloor - 1$ 未満の任意の自然数 $m$ に対し $m + 2$ が $n$ の約数ではない
がどちらも満たされることなので、素数判定関数 $\isPrime$ は以下のように定義できます。
\isPrime = \and \circ \left(
\begin{aligned}
\begin{gathered}
\isGreaterThanOrEqualTo \circ \left(
\begin{gathered}
P^1_1, \\
C^1_2
\end{gathered}
\right), \\
\forAll \left(
\begin{aligned}
\begin{gathered}
\predecessorOf \circ \squareRootOf \circ P^1_1, \\
\myNot \circ \isDivisibleBy \circ \left(
\begin{aligned}
\begin{gathered}
P^2_2, \\
\add \circ \left(
\begin{gathered}
P^2_1, \\
C^2_2
\end{gathered}
\right)
\end{gathered}
\end{aligned}
\right)
\end{gathered}
\end{aligned}
\right)
\end{gathered}
\end{aligned}
\right)
素数計数関数
これを用い、素数計数関数 $\countPrimes$ を定義します。
\countPrimes(n) := (\text{$n$ 未満の素数の個数})
ここで、$\countPrimes$ は明らかに以下の漸化式を満たします。
\begin{aligned}
\countPrimes(0) &= 0 \\
\countPrimes(S(n)) &=
\begin{cases}
S(\countPrimes(n)) & (\isPrime(n) = 1) \\
\countPrimes(n) & (\isPrime(n) = 0)
\end{cases}
\end{aligned}
よって $\countPrimes$ は原始再帰作用素で表せます。
\countPrimes = \rho \left(
\begin{gathered}
C^0_0, \\
\ifThenElse \circ \left(
\begin{gathered}
\isPrime \circ P^2_1, \\
S \circ P^2_2, \\
P^2_2
\end{gathered}
\right)
\end{gathered}
\right)
素数関数
さらに、引数で指定された番号の素数を返却する関数 $\nthPrime$ を定義します。つまりこういうことです。
\displaylines {
\nthPrime(0) = 2 \\
\nthPrime(1) = 3 \\
\nthPrime(2) = 5 \\
\nthPrime(3) = 7 \\
\nthPrime(4) = 11 \\
\vdots
}
ただし、上の例からも見て取れますが、素数は便宜上 0 番から数えるものとします($\nthPrime(0)$ だけ未定義になってしまうとスッキリしないので)。
まず(素数を 0 番から数える場合)$n$ 番目の素数 $p_n$ は不等式 $p_n < (n + 1)^2 + 2$ を満たします。
ちゃんと理解していませんが以下の回答を参考にしました。ただしリンク先の回答では素数を 1 番から数えていることに注意してください。
したがって $0$ 以上 $(n + 1)^2 + 2$ 未満の範囲内で $\countPrimes(k) = n \land \isPrime(k) = 1$ を満たす唯一の自然数 $k$ が必ず見つかります。この $k$ が $n$ 番目の素数 $p_n$ です。つまりさっき定義した限定的最小化作用素の出番ですね。
\nthPrime = \beta \left(
\begin{aligned}
\begin{gathered}
\add \circ \left(
\begin{gathered}
\multiply \circ \left(
\begin{gathered}
S, \\
S
\end{gathered}
\right), \\
C^1_2
\end{gathered}
\right), \\
\myNot \circ \and \circ \left(
\begin{aligned}
\begin{gathered}
\isEqualTo \circ \left(
\begin{gathered}
\countPrimes \circ P^2_1, \\
P^2_2
\end{gathered}
\right), \\
\isEqualTo \circ \left(
\begin{gathered}
\isPrime \circ P^2_1, \\
C^2_1
\end{gathered}
\right)
\end{gathered}
\end{aligned}
\right)
\end{gathered}
\end{aligned}
\right)
下準備 1: アッカーマン関数を数列で表現する
一旦話変わります。ここからアッカーマン関数の計算を別の観点から眺めてみます。ちょっと $\Ack(2, 1)$ を求めてみましょう。
\begin{aligned}
\Ack(2, 1) &= \Ack(1, \Ack(2, 0)) \\
&= \Ack(1, \Ack(1, 1)) \\
&= \Ack(1, \Ack(0, \Ack(1, 0))) \\
&= \Ack(1, \Ack(0, \Ack(0, 1))) \\
&= \Ack(1, \Ack(0, 2)) \\
&= \Ack(1, 3) \\
&= \Ack(0, \Ack(1, 2)) \\
&= \Ack(0, \Ack(0, \Ack(1, 1))) \\
&= \Ack(0, \Ack(0, \Ack(0, \Ack(1, 0)))) \\
&= \Ack(0, \Ack(0, \Ack(0, \Ack(0, 1)))) \\
&= \Ack(0, \Ack(0, \Ack(0, 2))) \\
&= \Ack(0, \Ack(0, 3)) \\
&= \Ack(0, 4) \\
&= 5
\end{aligned}
こうして実際の計算過程を眺めてみると $\Ack()$ がすごい入れ子になっているのが見て取れると思います。例として 9 行目を抜き出してみましょう。
\Ack(0, \Ack(0, \Ack(0, \Ack(1, 0))))
ここで一つ注目してほしい大事なことがあります。見ての通りすごい入れ子になっているこの式ですが、「閉じる括弧」は全て右側に集まっているのがわかると思います。
\Ack(0, \Ack(0, \Ack(0, \Ack(1, 0\color{red}{))))}
実際、「閉じる括弧」が全て右側に集中することになるのはアッカーマン関数の定義式から明らかです。
\Ack(m, n) =
\begin{cases}
n + 1 & (m = 0) \\
\Ack(m - 1, 1) & (m \neq 0, n = 0) \\
\Ack(m - 1, \Ack(m, n - 1)) & (m \neq 0, n \neq 0)
\end{cases}
ということはこのように、式から関数名 $\Ack$ 及び括弧を全て取ってしまっても、その意味に曖昧さが生じることはありません。
\displaylines {
\Ack(0, \Ack(0, \Ack(0, \Ack(1, 0)))) \\
\text{↕相互に一意的に変換可能} \\
0, 0, 0, 1, 0
}
関数名と括弧をすべて取ってしまっても、「後ろから二つとって $\Ack()$ でくくる」ということを繰り返せば元の式を復元できます。この発想により、アッカーマン関数の計算をこのように表現することができてしまいます。
$\Ack(m, n)$ を求めるにあたり、数列 $\boldsymbol{s} = \{m, n\}$ を用意する。数列 $\boldsymbol{s}$ に対し、その長さが 1 より大きい限り以下を繰り返す。
- $\boldsymbol{s}$ の末尾が $0, l$ ならばこの二つを取り去り、$l + 1$ を末尾に追加する。
- $\boldsymbol{s}$ の末尾が $k (\neq 0), 0$ ならばこの二つを取り去り、$k - 1, 1$ を末尾に追加する。
- $\boldsymbol{s}$ の末尾が $k (\neq 0), l (\neq 0)$ ならばこの二つを取り去り、$k - 1, k, l - 1$ を末尾に追加する。
$\boldsymbol{s}$ の長さが 1 になったとき、$\boldsymbol{s}$ に含まれるその唯一の自然数がアッカーマン関数の解である。
def sequential_Ackermann(m, n):
s = [m, n]
while len(s) > 1:
l = s.pop()
k = s.pop()
if m == 0:
s += [l + 1]
elif n == 0:
s += [k - 1, 1]
else:
s += [k - 1, k, l - 1]
return s[0]
下準備 2: 自然数列を自然数にエンコードする
ここに自然数列 $\boldsymbol{s} = \{s_i\}$ があるとします。この数列 $\boldsymbol{s}$ のエンコード $\encode(\boldsymbol{s})$ を以下のように定義します。
\encode(\boldsymbol{s}) := \prod_{i = 0}^{|\boldsymbol{s}| - 1} p_i^{s_i + 1} \ (\text{$p_i$ は $i$ 番目の素数})
いくつか具体例を見てみましょう。
\begin{aligned}
&\encode(\{0\}) &&= 2^{0 + 1} &&= 2 \\
&\encode(\{0, 1\}) &&= 2^{0 + 1} \times 3^{1 + 1} &&= 18 \\
&\encode(\{1\}) &&= 2^{1 + 1} &&= 4 \\
&\encode(\{3, 6, 2, 9\}) &&= 2^{3 + 1} \times 3^{6 + 1} \times 5^{2 + 1} \times 7^{9 + 1} &&= 1235546739126000
\end{aligned}
このように自然数列を自然数へ変換することができます。またそれ以上に重要なのは、この変換は元に戻せるということです。この変換は素因数分解の一意性を利用しているので、変換後の自然数を素因数分解して各要素から $1$ を引いてやれば元の数列を復元できるというわけです。
ただ残念ながら、この方法は自然数列と自然数を一対一で対応させるものではありません(単射ではあるものの全射ではない)。例えば自然数 $10$ に対応する数列を強引に求めると $\{0, -1, 0\}$ と $-1$ を含むものになってしまいます。ただこのことはこの後の議論とは関係ないのでこのまま進めます。全単射を作る方法も思いつかなかったし
同様に、自然数のデコード $\decode(e)$ を以下のように定めます。
\decode(e) := (\text{エンコード結果が $e$ であるような数列})
アッカーマン関数を最小化作用素で表す
アッカーマン関数を「数列から数列の変換」として表現する方法はすでに述べた通りです。この発想を用い、以下を定めます。
s_{m, n, i} := (\text{$\{m, n\}$ から始まるアッカーマン数列を $i$ 回変換したもの})
意味わかんないので具体例を見てみましょう。まず一例として、$\Ack(1, 1)$ は以下のように求まります。
\begin{aligned}
\Ack(1, 1) &= \Ack(0, \Ack(1, 0)) \\
&= \Ack(0, \Ack(0, 1)) \\
&= \Ack(0, 2) \\
&= 3
\end{aligned}
したがって各 $i$ に対し $s_{1, 1, i}$ は以下のように定まります。
\begin{aligned}
s_{1, 1, 0} &= \{1, 1\} \\
s_{1, 1, 1} &= \{0, 1, 0\} \\
s_{1, 1, 2} &= \{0, 0, 1\} \\
s_{1, 1, 3} &= \{0, 2\} \\
s_{1, 1, 4} &= \{3\}
\end{aligned}
さて、数列に対する操作は数列の長さが $1$ になったらおしまいなのでした。したがって、最小化作用素を用いてアッカーマン関数はこのように表せます。
\displaylines {
\lengthOf(e) := (\text{エンコードが $e$ である数列の長さ}) \\
\subscript(e, i) := (\text{エンコードが $e$ である数列の $i$ 番目の要素}) \\
\AckSeq(m, n, i) := \encode(s_{m, n, i}) \\
\begin{aligned}
\finalIndexOf(m, n) &:= (\text{$\lengthOf(\AckSeq(m, n, i)) = 1$ を満たす最小の $i$}) \\
&= \mu(\myNot \circ \isEqualTo \circ (\lengthOf \circ \AckSeq \circ (P^3_2, P^3_3, P^3_1), C^3_1))(m, n)
\end{aligned} \\
\begin{aligned}
\Ack(m, n) &= (\text{$s_{m, n, \finalIndexOf(m, n)}$ の唯一の要素}) \\
&= (\text{$\decode(\AckSeq(m, n, \finalIndexOf(m, n)))$ の唯一の要素}) \\
&= \subscript(\AckSeq(m, n, \finalIndexOf(m, n)), 0)
\end{aligned}
}
よって、アッカーマン関数 $\Ack$ が $\mu$ 再帰関数であることを証明するには以下が証明できればよいです。
- $\subscript$ が $\mu$ 再帰関数であること
- $\AckSeq$ が $\mu$ 再帰関数であること
- $\finalIndexOf$ が $\mu$ 再帰関数であること
- さらに上記の $\finalIndexOf$ の式より、$\finalIndexOf$ の $\mu$ 再帰性の証明には以下を示せば十分です。
- $\lengthOf$ が $\mu$ 再帰関数であること
- $\AckSeq$ が $\mu$ 再帰関数であること
- さらに上記の $\finalIndexOf$ の式より、$\finalIndexOf$ の $\mu$ 再帰性の証明には以下を示せば十分です。
というわけで、$\lengthOf$, $\subscript$, $\AckSeq$ の $\mu$ 再帰性を示せばめでたくアッカーマン関数の $\mu$ 再帰性が示せたことになります。$\lengthOf$ と $\subscript$ の二つに関してはもしかしたら単に $\mu$ 再帰関数であるのみならず原始再帰関数であることも示せるのかもしれませんが、もう面倒なのでこの記事では $\mu$ 再帰性を示すにとどめます。
lengthOf の μ 再帰性
まず $\lengthOf$ の方ですが、$\lengthOf(e)$ は「$e$ の素因数でない最小の素数の番号」とも表現できます(素数は 0 番から数えると約束していたことに注意してください)。ということは最小化作用素を使えば簡単に表現できますね。
\lengthOf = \mu(\isDivisibleBy \circ (P^2_2, \nthPrime \circ P^2_1))
subscript の μ 再帰性
次に $\subscript$ ですが、$\subscript(e, i)$ は「$p_i^k$ が $e$ を割り切らなくなる最小の $k$ に対する $k - 2$」と表現できます。ということはこうなります。
\subscript = \subtract \circ \left(
\begin{gathered}
\mu \left(
\isDivisibleBy \circ \left(
\begin{gathered}
P^3_2, \\
\exponentiate \circ \left(
\begin{gathered}
\nthPrime \circ P^3_3, \\
P^3_1
\end{gathered}
\right)
\end{gathered}
\right)
\right) \\
C^2_2
\end{gathered}
\right)
lastOf
いま定義した $\lengthOf$ と $\subscript$ を組み合わせると数列の末尾要素を取り出す $\lastOf$ がついでに定義できます。
\lastOf = \subscript \circ (P^1_1, \predecessorOf \circ \lengthOf)
javascript なんかで配列の最後の要素を取得するのに array[array.length - 1] とかやるのと全く同じことですね。
AckSeq の μ 再帰性
次に以下の演算をどんどこ定めていきます。
\displaylines {
\pushed(e, n) := (\text{エンコードが $e$ である数列の末尾に $n$ を追加した数列のエンコード}) \\
\popped(e) := (\text{エンコードが $e$ である数列の末尾の要素を削除した数列のエンコード})
}
$\pushed(e, n)$ の方は $e \times p_{|\decode(e)|}^{n + 1}$ と表せます。したがってこうなります。
\pushed = \multiply \circ \left(
\begin{gathered}
P^2_1, \\
\exponentiate \circ \left(
\begin{gathered}
\nthPrime \circ \lengthOf \circ P^2_1, \\
S \circ P^2_2
\end{gathered}
\right)
\end{gathered}
\right)
次に $\popped(e)$ の方は $\frac{e}{p_{|\decode(e)| - 1}^{\lastOf(e) + 1}}$ となるのでこうなります。
\popped = \divide \circ \left(
\begin{gathered}
P^1_1, \\
\exponentiate \circ \left(
\begin{gathered}
\nthPrime \circ \predecessorOf \circ \lengthOf \circ P^1_1, \\
S \circ \lastOf \circ P^1_1
\end{gathered}
\right)
\end{gathered}
\right)
これらを用いて $\AckSeq$ はこうなります。
\begin{aligned}
\AckSeq(m, n, 0) &= \encode(\{m, n\}) \\
&= 2^{m + 1} \times 3^{n + 1} \\
\AckSeq(m, n, S(i)) &=
\begin{cases}
\pushed(\popped(\popped(\AckSeq(m, n, i))), l + 1) & (\text{末尾が $0, l$}) \\
\pushed(\pushed(\popped(\popped(\AckSeq(m, n, i))), k - 1), 1) & (\text{末尾が $k (\neq 0), 0$}) \\
\pushed(\pushed(\pushed(\popped(\popped(\AckSeq(m, n, i))), k - 1), k), l - 1) & (\text{末尾が $k (\neq 0), l (\neq 0)$})
\end{cases}
\end{aligned}
これでようやく $\AckSeq$ を定義するためのお膳立てが整いました。あとはごにょごにょするとこうなります。
\AckSeq = \rho \left(
\begin{gathered}
\multiply \circ \left(
\begin{gathered}
\exponentiate \circ \left(
\begin{gathered}
C^2_2, \\
S \circ P^2_1
\end{gathered}
\right), \\
\exponentiate \circ \left(
\begin{gathered}
C^2_3, \\
S \circ P^2_2
\end{gathered}
\right)
\end{gathered}
\right), \\
\ifThenElse \circ \left(
\begin{gathered}
\isZero \circ \left(
\begin{gathered}
\lastOf, \\
\popped \circ P^4_2
\end{gathered}
\right), \\
\pushed \circ \left(
\begin{gathered}
\popped \circ \popped \circ P^4_2, \\
S \circ \lastOf \circ P^4_2
\end{gathered}
\right), \\
\ifThenElse \circ \left(
\begin{gathered}
\and \left(
\begin{gathered}
\isZero \circ \lastOf \circ P^4_2, \\
\myNot \circ \isZero \circ \lastOf \circ \popped \circ P^4_2
\end{gathered}
\right), \\
\pushed \circ \left(
\begin{gathered}
\pushed \circ \left(
\begin{gathered}
\popped \circ \popped \circ P^4_2, \\
\predecessorOf \circ \lastOf \circ \popped \circ P^4_2
\end{gathered}
\right), \\
C^4_1
\end{gathered}
\right), \\
\pushed \circ \left(
\begin{gathered}
\pushed \circ \left(
\begin{gathered}
\pushed \circ \left(
\begin{gathered}
\popped \circ \popped \circ P^4_2, \\
\predecessorOf \circ \lastOf \circ \popped \circ P^4_2
\end{gathered}
\right), \\
\lastOf \circ \popped \circ P^4_2
\end{gathered}
\right), \\
\predecessorOf \circ \lastOf \circ P^4_2
\end{gathered}
\right)
\end{gathered}
\right)
\end{gathered}
\right)
\end{gathered}
\right) \circ \left(
\begin{gathered}
P^3_3, \\
P^3_1, \\
P^3_2
\end{gathered}
\right)
長すぎンだろ・・・
アッカーマン関数(再掲)
これでようやく $\AckSeq$ が定義できました。よって先ほどにも述べたようにアッカーマン関数 $\Ack$ がこのように定義できます。
\displaylines {
\finalIndexOf = \mu \left(
\myNot \circ \isEqualTo \circ \left(
\begin{gathered}
\lengthOf \circ \AckSeq \circ \left(
\begin{gathered}
P^3_2, \\
P^3_3, \\
P^3_1
\end{gathered}
\right), \\
C^3_1
\end{gathered}
\right)
\right) \\
\Ack = \subscript \circ \left(
\begin{gathered}
\AckSeq \circ \left(
\begin{gathered}
P^2_1, \\
P^2_2, \\
\finalIndexOf \circ P^2_1 \circ P^2_2
\end{gathered}
\right), \\
C^2_0
\end{gathered}
\right)
}
これでようやく定義完了です。お疲れさまでした。
注意点
前述の通り Python で実装したソースコードを公開しています。この実装は検算も兼ねていたのですが、しかし原始再帰関数はアホみたいに再帰しまくるのでアッカーマン関数はせいぜい $\Ack(1, 1) = 3$ くらいまでしか確認できませんでした。なのでもしかしたら立式を間違えている部分もあるかもしれませんが、もう私の知ったこっちゃありません(半ギレ)
おまけ
この記事のおまけとして、衝撃的事実をご紹介します。
アッカーマン関数は原始再帰的ではないと証明したわけですが、アッカーマン関数に少し制限を加えたこんな関数を考えてみましょう。
\Ack_0(n) = \Ack(0, n)
つまり、$\Ack_0$ はアッカーマン関数の第一引数を $0$ に固定した関数です。アッカーマン関数の定義よりこの関数の返り値はこうなります。
\Ack_0(n) = n + 1
この $\Ack_0$ は明らかに原始再帰的です。具体的には $\Ack_0 = S$ です。
次に $\Ack_1$ について考えてみましょう。つまりアッカーマン関数の第一引数を $1$ に固定した関数です。
\begin{aligned}
\Ack_1(n) &= \Ack(1, n) \\
&=
\begin{cases}
\Ack(0, 1) & (n = 0) \\
\Ack(0, \Ack(1, n - 1)) & (n \neq 0)
\end{cases} \\
&=
\begin{cases}
\Ack_0(1) & (n = 0) \\
\Ack_0(\Ack_1(n - 1)) & (n \neq 0)
\end{cases}
\end{aligned}
$n \neq 0$ の場合を再帰的に展開していくと以下のようになります。
\displaylines {
\Ack_1(n) = \underbrace{\Ack_0(\Ack_0(\ldots \Ack_0(1)))}_{\text{$n + 1$ $\Ack_0(\cdot)$s}} \\
\therefore \Ack_1 = \rho(C^0_1, \Ack_0 \circ P^2_2) \circ S
}
したがって、$\Ack_0$ が原始再帰的であったことから $\Ack_1$ も原始再帰的です。
このことは $\Ack_2$ 以降も同様です。一般に $\Ack_{i + 1}$ は $\Ack_1$ と $\Ack_0$ の関係式と同様に
\Ack_{i+1} = \rho(C^0_1, \Ack_i \circ P^2_2) \circ S
と表せるので、帰納的に任意の $i$ に対し $\Ack_i$ は原始再帰的です。これが衝撃的事実です。$\Ack_0$ も $\Ack_1$ も $\Ack_2$ も $\Ack_{100}$ も $\Ack_{18363285803}$ も原始再帰的なのに、にもかかわらずアッカーマン関数 $\Ack$ は非原始再帰的なのです。
せっかくなのでもう少し深堀りして考えてみましょう。原始再帰作用素が for 文を表すというのはすでに述べた通りです。したがって、原始再帰作用素を 1 個使って表せる $\Ack_1$ は 1 重ループに相当します。
\begin{aligned}
\Ack_1 &= \rho(C^0_1, \Ack_0 \circ P^2_2) \circ S \\
&= \rho(C^0_1, S \circ P^2_2) \circ S
\end{aligned}
そして $\Ack_2$ はこのように原始再帰作用素を二つ入れ子にして表せるので、すなわち 2 重ループに相当します。
\begin{aligned}
\Ack_2 &= \rho(C^0_1, \Ack_1 \circ P^2_2) \circ S \\
&= \rho(C^0_1, \rho(C^0_1, S \circ P^2_2) \circ S \circ P^2_2) \circ S
\end{aligned}
以下同様です。$\Ack_{100}$ は 100 重ループに相当しますし、$\Ack_{18363285803}$ は 18363285803 重ループに相当します。これらは全てまぎれもない原始再帰関数です。
ですが、アッカーマン関数 $\Ack(m, n)$ は $m$ 重ループを表します。つまり、アッカーマン関数を計算するには for 文の深さ自体を動的に決める必要があるのです。それが原始再帰関数の表現能力を超えてしまっており、アッカーマン関数は原始再帰関数では表せないというわけです。
おまけ 2
最後にアッカーマン関数の一般項を求めてみましょう。まず $\Ack_0(n) = n + 1$ なので $S(n)$ と一致することはすでに述べた通りです。
\Ack_0 = S
そして $\Ack_1$ と $\Ack_0$ の間にはこのような関係が成り立つのでした。
\Ack_1(n) = \underbrace{\Ack_0(\Ack_0(\ldots \Ack_0(1)))}_{\text{$n + 1$ $\Ack_0(\cdot)$s}}
つまり、$\Ack_1(n)$ は「$1$ に『$1$ を足す』を $n + 1$ 回繰り返した値」になります。したがって $\Ack_1$ の一般項はこのようになります。
\Ack_1(n) = n + 2
これは「性質 1」としてずっと前に求めましたね。
次に $\Ack_2$ は $\Ack_1$ を用いて以下のように表せます。
\Ack_2(n) = \underbrace{\Ack_1(\Ack_1(\ldots \Ack_1(1)))}_{\text{$n + 1$ $\Ack_1(\cdot)$s}}
よって $\Ack_2(n)$ の一般項は以下のように求まります。
\begin{aligned}
\Ack_2(n) &= \underbrace{(((1) + 2) + 2 ) + \cdots + 2}_{\text{$n + 1$ times}} \\
&= 2n + 3
\end{aligned}
これも「性質 2」として求めたやつですね。
この調子で $\Ack_3$ も求めていきましょう。ここまでくれば同じ感じなのでもうはしょっていきます。
\begin{aligned}
\Ack_3(n) &= \underbrace{2 \times (\cdots (2 \times (2 \times (1) + 3) + 3) \cdots) + 3}_{\text{$n + 1$ times}} \\
&= \underbrace{2 \times (\cdots (2 \times (2^2 \times (1) + 3 \times 2 + 3) + 3) \cdots) + 3}_{\text{$n$ times}} \\
&= \underbrace{2 \times (\cdots (2 \times (2^3 \times (1) + 3 \times 2^2 + 3 \times 2 + 3) + 3) \cdots) + 3}_{\text{$n - 1$ times}} \\
&= \cdots \\
&= 2^{n + 1} \times (1) + 3 \times (2^n + 2^{n - 1} + \cdots + 1) \\
&= 2^{n + 1} + 3 \times (2^{n + 1} - 1) \\
&= 2^{n + 1} + 3 \times 2^{n + 1} - 3 \\
&= 4 \times 2^{n + 1} - 3 \\
&= 2^{n + 3} - 3
\end{aligned}
もう少し頑張って $\Ack_4$ も求めます。
\begin{aligned}
\Ack_4(n) &= \underbrace{2^{{\iddots}^{2^{(2^{(1) + 3} - 3) + 3} - 3_\ddots}} - 3}_{\text{$n + 1$ times}} \\
&= \underbrace{2^{{\iddots}^{2^4}}}_{\text{$n + 1$ times}} - 3 \\
&= \underbrace{2^{{\iddots}^{2^2}}}_{\text{$n + 3$ times}} - 3
\end{aligned}
クヌースの矢印とハイパー演算
そろそろ表記が辛くなってきました。しかも次の $\Ack_5$ はもっと辛くなるでしょう。そこでクヌースの矢印表記というものを導入することで少しでも読みやすくします。
まず演算子 "$\uparrow$" は冪乗を表すものとします。
m \uparrow n := m^n
次に演算子 "$\uparrow\uparrow$" を定めます。これはさっき定義した演算子 "$\uparrow$" を二つ並べたものではなく、この矢印二つで一塊の演算子です。
\begin{aligned}
m \uparrow\uparrow n &:= \underbrace{m \uparrow (\cdots \uparrow (m \uparrow m))}_{\text{$n$ times}} \\
&= \underbrace{m^{m^{{\iddots}^m}}}_{\text{$n$ times}}
\end{aligned}
つまり、冪乗を繰り返すことで演算 "$\uparrow\uparrow$" が定められます。これは足し算の繰り返しにより掛け算を定義したり、掛け算の繰り返しにより冪乗を定義したりしたのと全く同じパターンです。並べてみると共通性がよくわかります(ただし冪乗以降は結合法則が成り立たなくなるので括弧が必要になることに注意してください)。
\displaylines {
m \times n = \underbrace{m + m + \cdots + m}_{\text{$n$ times}} \\
m \uparrow n = \underbrace{m \times m \times \cdots \times m}_{\text{$n$ times}} \\
m \uparrow\uparrow n = \underbrace{m \uparrow (\cdots \uparrow (m \uparrow m))}_{\text{$n$ times}}
}
同じ調子で演算子 "$\uparrow\uparrow\uparrow$" も定めましょう。
\begin{aligned}
m \uparrow\uparrow\uparrow n &:= \underbrace{m \uparrow\uparrow (\cdots \uparrow\uparrow (m \uparrow\uparrow m))}_{\text{$n$ times}} \\
&= \left. \underbrace{m^{m^{{\iddots}^m}}}_{\underbrace{\vdots}_{\text{$\underbrace{m^{m^{{\iddots}^m}}}_{\text{$\underbrace{m^{m^{{\iddots}^m}}}_{\text{$m$ times}}$ times}}$ times}}} \right\} \text{$n$ times}
\end{aligned}
もはや $\TeX$ ですら描画が厳しくなってきたのでここらで打ち止めにしますが、この後も "$\uparrow\uparrow\uparrow\uparrow$", "$\uparrow\uparrow\uparrow\uparrow\uparrow$", ... と凶悪な演算子が際限なく定義されていきます。これら足し算、掛け算、冪乗、"$\uparrow\uparrow$"(テトレーション)、"$\uparrow\uparrow\uparrow$"(ペンテーション)・・・を総称してハイパー演算といいます。足し算を「レベル 1 のハイパー演算」、掛け算を「レベル 2 のハイパー演算」などと呼ぶことにすると、レベル $i$ のハイパー演算 $\hyper_i$ は以下のように定義されます。
\hyper_i(m, n) =
\begin{cases}
n + 1 & (i = 0) \\
m & (i = 1 \land n = 0) \\
0 & (i = 2 \land n = 0) \\
1 & (i \geq 3 \land n = 0) \\
\hyper_{i - 1}(m, \hyper_i(m, n - 1)) & (\mathrm{otherwise})
\end{cases}
きれいな再帰的定義になるかと思いきや意外とごちゃごちゃしてしまいました。なんで・・・?
そしてレベル 0 の演算は便宜的に $\hyper_0(m, n) = n + 1$ となります。$m$ がどっか行っちゃってますが定義の一貫性のためですから仕方ありません。
アッカーマン関数をハイパー演算で表す
これまでに一般項がわかった $\Ack_0$ から $\Ack_4$ を並べてみましょう。
\begin{aligned}
\Ack_0(n) &= n + 1 \\
\Ack_1(n) &= n + 2 \\
\Ack_2(n) &= 2n + 3 \\
\Ack_3(n) &= 2^{n + 3} - 3 \\
&= 2 \uparrow (n + 3) - 3 \\
\Ack_4(n) &= \underbrace{2^{{\iddots}^{2^2}}}_{\text{$n + 3$ times}} - 3 \\
&= 2 \uparrow\uparrow (n + 3) - 3
\end{aligned}
ここから話の流れが強引になります $\Ack_4$ は見ての通り "$\uparrow\uparrow$"(テトレーション)で表されます。そして $\Ack_3$ は冪乗で表されます。ということは、$\Ack_i$ はレベル $i$ のハイパー演算で表せそうですよね?
そして $\Ack_3$ と $\Ack_4$ にもう一度注目してみましょう。
\begin{aligned}
\Ack_3(n) &= 2 \uparrow (n + 3) - 3 \\
\Ack_4(n) &= 2 \uparrow\uparrow (n + 3) - 3
\end{aligned}
なんか似てます。そして実は $\Ack1$ と $\Ack_2$ もこれと似た形で表されます。
\begin{aligned}
\Ack_1(n) &= n + 2 \\
&= 2 + (n + 3) - 3 \\
\Ack_2(n) &= 2n + 3 \\
&= 2 \times (n + 3) - 3
\end{aligned}
つまりこのような仮説が立てられます。
\Ack_m(n) = \hyper_m(2, n + 3) - 3
$m = 1, 2, 3, 4$ でしか確かめていませんでしたが、$m = 0$ でも成り立つでしょうか?
\begin{aligned}
\Ack_0(n) &= n + 1 \\
&= (n + 3) + 1 - 3 \\
&= \hyper_0(2, n + 3) - 3
\end{aligned}
見事に成り立ちました。仮説の信憑性は高そうです。それではきちんと証明しましょう。
証明
まず以下の補題を証明する。
補題: 任意の $i \geq 1$ に対し、$\hyper_i(2, 2) = 4$ である。
証明: ハイパー演算子の定義より任意の自然数 $m$ 及び $3$ 以上の任意の $i$ に対し $\hyper_{i}(m, 0) = 1$ であることに注意すると、$2$ 以上の任意の $i'$ に対し
\begin{aligned}
\hyper_{i'}(m, 1) &= \hyper_{i'}(m, \hyper_{i' + 1}(m, 0)) \\
&= \hyper_{i' + 1}(m, 1)
\end{aligned}
が成立する。そして $\hyper_2(m, 1) = m \times 1 = m$ なので、したがって帰納的に $2$ 以上の任意の $i$ に対し $\hyper_{i}(m, 1) = m$ である。よって $1$ 以上の任意の $i'$ に対し、
\begin{aligned}
\hyper_{i'}(2, 2) &= \hyper_{i'}(2, \hyper_{i' + 1}(2, 1)) \\
&= \hyper_{i' + 1}(2, 2)
\end{aligned}
が成立する。そして $\hyper_1(2, 2) = 2 + 2 = 4$ なので、したがって帰納的に $1$ 以上の任意の $i$ に対し $\hyper_{i}(2, 2) = 4$ である。(証明終)
とある $m'$ が存在して任意の $n$ に対し $\Ack(m', n) = \hyper_{m'}(2, n + 3) - 3$ であると仮定すると、
\begin{aligned}
\Ack(m' + 1, n) &= \Ack(m', \Ack(m' + 1, n - 1)) \\
&= \hyper_{m'}(2, \Ack(m' + 1, n - 1) + 3) - 3 & (\because \text{仮定より}) \\
&= \hyper_{m'}(2, \Ack(m', \Ack(m' + 1, n - 2)) + 3) - 3 \\
&= \hyper_{m'}(2, \hyper_{m'}(2, \Ack(m' + 1, n - 2) + 3) \cancel{- 3 + 3}) - 3 & (\because \text{仮定より}) \\
&= \cdots \\
&= \underbrace{\hyper_{m'}(2, \hyper_{m'}(2, \cdots \hyper_{m'}(2, \Ack(m' + 1, 0) + 3) \cdots ))}_{\text{$n$ $\hyper_{m'}(\cdot, \cdot)$s and $\Ack(\cdot)$}} - 3 \\
&= \underbrace{\hyper_{m'}(2, \hyper_{m'}(2, \cdots \hyper_{m'}(2, \Ack(m', 1) + 3) \cdots ))}_{\text{$n$ $\hyper_{m'}(\cdot, \cdot)$s and $\Ack(\cdot)$}} - 3 \\
&= \underbrace{\hyper_{m'}(2, \hyper_{m'}(2, \cdots \hyper_{m'}(2, \hyper_{m'}(2, 1 + 3) \cancel{- 3 + 3}) \cdots ))}_{\text{$n + 1$ $\hyper_{m'}(\cdot, \cdot)$s}} - 3 & (\because \text{仮定より}) \\
&= \underbrace{\hyper_{m'}(2, \hyper_{m'}(2, \cdots \hyper_{m'}(2, \hyper_{m'}(2, 4)) \cdots ))}_{\text{$n + 1$ $\hyper_{m'}(\cdot, \cdot)$s}} - 3
\end{aligned}
ここで $m' = 0$ の場合と $m' > 0$ の場合を考える。$m' = 0$ のときレベル 0 のハイパー演算 $\hyper_0$ は第 2 引数に $1$ を足すだけなので、
\begin{aligned}
& \underbrace{\hyper_{m'}(2, \hyper_{m'}(2, \cdots \hyper_{m'}(2, \hyper_{m'}(2, 4)) \cdots ))}_{\text{$n + 1$ $\hyper_{m'}(\cdot, \cdot)$s}} - 3 \\
={} & 4 + 1 \times (n + 1) - 3 \\
={} & n + 2 \\
={}& \hyper_1(2, n + 3) - 3
\end{aligned}
よって $m' = 0$ のときは $\Ack(m' + 1, n) = \hyper_{m' + 1}(2, n + 3) - 3$ が成立する。また $m' > 0$ のときは、
\begin{aligned}
& \underbrace{\hyper_{m'}(2, \hyper_{m'}(2, \cdots \hyper_{m'}(2, \hyper_{m'}(2, 4)) \cdots ))}_{\text{$n + 1$ $\hyper_{m'}(\cdot, \cdot)$s}} - 3 \\
={} & \underbrace{\hyper_{m'}(2, \hyper_{m'}(2, \cdots \hyper_{m'}(2, \hyper_{m'}(2, \hyper_{m'}(2, 2))) \cdots ))}_{\text{$n + 2$ $\hyper_{m'}(\cdot, \cdot)$s}} - 3 & (\because \text{補題より}) \\
={} & \hyper_{m' + 1}(2, n + 3) - 3
\end{aligned}
よって $m' > 0$ のときも $\Ack(m' + 1, n) = \hyper_{m' + 1}(2, n + 3) - 3$ が成立する。したがって任意の $m'$ に対し $\Ack(m' + 1, n) = \hyper_{m' + 1}(2, n + 3) - 3$ が成立する。
$m = 0$ のとき仮定が成立することは確認済みなので、よって帰納的に任意の $m$ に対し与命題は成立する。(証明終)
そんなわけでアッカーマン関数の一般項はハイパー演算で表せるとわかりました。またこのことからハイパー演算も非原始再帰的であることがわかります。言うまでもないことですが、もしハイパー演算が原始再帰的であるならばそれを使って表せるアッカーマン関数も原始再帰的ということになってしまいますからね。
もちろん足し算・掛け算・冪乗などの「各」ハイパー演算は原始再帰的ですが、それでも一般のレベルに対するハイパー演算は原始再帰的ではありません。各 $i$ に対する $\Ack_i$ は原始再帰的だったのにアッカーマン関数 $\Ack$ は原始再帰的でなかったのと同じことですね。
おわりに
知っていることは全部書いたのでこれで終わりです。オチとか思いつきませんでした。~おわり~