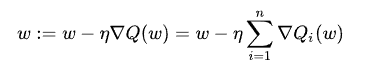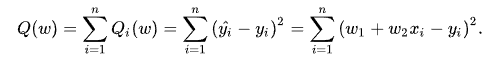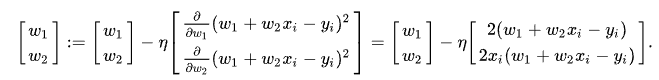強化学習のお勉強をしているのだが、どうやらSGDというのを学ばねばならぬと分かったのでやってみた。
数式萌の方は、上記の記事を読んで満足されたし。コードを書かねぇとよぉ、ぷろぐらまーはよぉ、ダメだぜぇ!というガテン系のあなたは、ここにきて正解だぞ!
確率的勾配降下法
みんな、覚えているかい?世間がディープラーニング、ディープラーニングと騒いでいた時のことを…あれはそう、たぶん4~5年前だっけか。そのくらいの時期だった気がする。グーグル猫というのが話題になり、猫も杓子もディープラーニング、ディープラーニングとか言っちゃって、このままだと人類はスカイネットに滅ぼされる、そんな雰囲気でした。
そのとき、陰の立役者として名を馳せていたのがご存じSGD(確率的勾配降下法)でした。当初はどんな高等なアルゴリズムなのか…と私も好奇心いっぱいで、主にsklearnのSGDRegresstionとかを使って、分かった気になっていました。まー、一時の熱に浮かされただけの、なんだ、俺もちょっと「ディープラーニング」の流行に乗り遅れちゃヤバイし、みたいな、そういう…ね。ただ、仕事になりそうなのはReactだよね!あとVue.jsね!
というわけで、SGDの数式を見てみよう:
これが、SGDだぜ!思ったより簡単そうじゃん、と思ったそこのあなた——その通り、思ったより簡単である。コードにすると、次の通り:
import numpy as np
import matplotlib.pyplot as plt
# w - パラメータのベクトル
# xs - なんかのデータ
# alpha - 学習率
# grad - これは…皆さんも大好きなでんでんむしのあれ
def sgd(grad, xs, w, alpha):
for x in xs:
w = w - alpha * grad(x, w)
return w
マジで、こんだけである。いやー、こんなことなら、早く勉強して、6年くらい前にディープラーニング、ディープラーニングって言っとけばよかったわ。と、現実はそんなに甘くなく、実はSGDは簡単でも、このgradと言うやつがそれほど簡単ではない。そう、皆さんもご存じの、でんでんむしである。
さて、日本語版WikipediaだとこのQが何だかさっぱり分からないんだけど、英語版を見ると簡単な例が載っているので分かるぞ!Qとは、こんなやつ!
この場合、いわゆる「せんけいかいき」の問題なので、Qはこのような形になるが、どんな最適化をしたいのか?によってQの形は変わるので要注意だ。そして、Qは線形和でなければならないそうなので「のんりにあ」な誤差関数の最適化には使えないぞ。
一応、念のため説明するが、式の形を見ての通り、これは二乗誤差になります。最適化しようとしている関数の関数形は、この場合線形回帰なのでy = a*x + bです、念のため。推定したい関数、想定しているモデル、なんでも良いが、そっちじゃなくて、それとデータの差を取って二乗した誤差の関数ね。で、gradで計算するのは…
ぐは!でんでんむし。というわけで、Qをパラメータwについて偏微分したものが、gradで計算されるものなので注意しような!もちろん、「にゅーらるねっと」のようなモデルに対してこんなものを計算したら、でんでんむしが大量発生して正気を失ってしまいます。だから、イケイケのお姉さんやお兄さんたちはChainerとか、Tensor Flowとかを使って、そういう計算を自動でコンピューターにやらせてるんだね。でも、僕ら小市民はそんな大きな問題をとけるほど、性能がいいマシンは持っていない。それになにより、白クマさんたちのことを考えなければ!
温暖化の危機にさらされている「ほっきょくのしろくま」さんたちは、君が無駄にCPUを回して、無駄に電力を消費するのを止める日を、心待ちにしている!
あと、ちょっと本題から外れるけど、マイクロソフト、おまえな!Compatibility Telemetryとかいう変なプログラム動かして、ホッキョクグマを死に追いやるのはやめろな!温暖化対策に協力しますとか、口だけ言ってさ。あとグーグル!お前らも、エコなお兄さん、お姉さんですって顔してるけど、Chorome入れたら変なプログラム(SoftwareReporter.exe)走ってCPU凄いまわるよ?全世界だからな、全世界。無駄な電気使うなよな!アンタらが回したCPU代はうちの電気代に計上されるんだからさ。エクスペリエンスなんて向上させなくていいから、CPU無駄に回すのやめれ。
あー、これはSGDじゃないや、SDGSか。なんか、つい、人類の未来を案ずるあまり、心の叫びが出てしまったわ。
線形回帰してみる
さて、SGDの何がうれしいのかというと、嬉しいことがいくつかある。
- 見ての通り、簡単。予測に活かすデータ分析って本で、樋口先生って方が「複雑なアルゴリズムは性能よくてもあんましつかわれねーな」とおっしゃっていたが、まさにその通りだと思う。実装が、簡単。改造も簡単。
- いっぺんにデータを入れなくともよい。いわゆる、オンライン型のアルゴリズム。
- 見ての通り、大した計算はしていないので、はやい
というわけで、いいとこづくめのアルゴリズムなのだ!では、さっそく線形回帰してみるなり。
# さっきと同じ。trに最適化のトレースを記録するようにしただけ。
def sgd2(grad, xs, w, alpha=0.01):
tr = []
for x in xs:
w = w - alpha * grad(x, w)
tr.append(w)
return w, tr
# でんでんむしの計算
# δy^2/δa、δy^2/δbのように二乗誤差を(xとかyでなくて)パラメータで偏微分した式。
def grad(xs, w):
a, b = w
x, y = xs
xgrad = -2 * xs[0] * (y-(a*x+b))
ygrad = -2 * (y-(a*x+b))
return np.array([xgrad, ygrad])
a = 5
b = -4
xs, ys = [], []
# y = 5*x - 4 を生成。適当なノイズをのせとく。
for x in np.arange(-1, 1, 0.001):
noise = np.random.normal(0.0, 1.0)
xs.append(x)
ys.append(a * x + b + noise)
# パラメータwはax+bなのでa,bで二つ!初期値は両方ゼロ!
w = np.array([0.0, 0.0])
# データの整形と、シャッフル
xsys = np.vstack([xs,ys]).T
np.random.shuffle(xsys)
# 最適化!
w, tr = sgd(grad, xsys, w)
tr = np.array(tr)
f, ax = plt.subplots(1,2)
ax[0].plot(tr[:,0], tr[:,1])
ax[1].plot(tr[:,0])
ax[1].plot(tr[:,1])
ax[1].set_xscale('log')
plt.show()
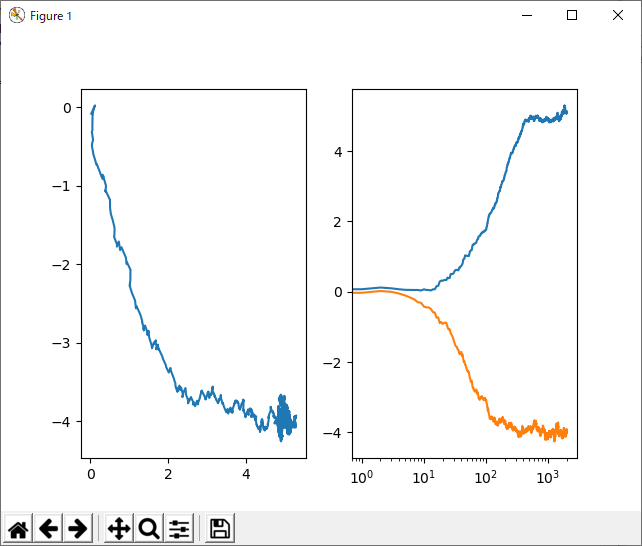
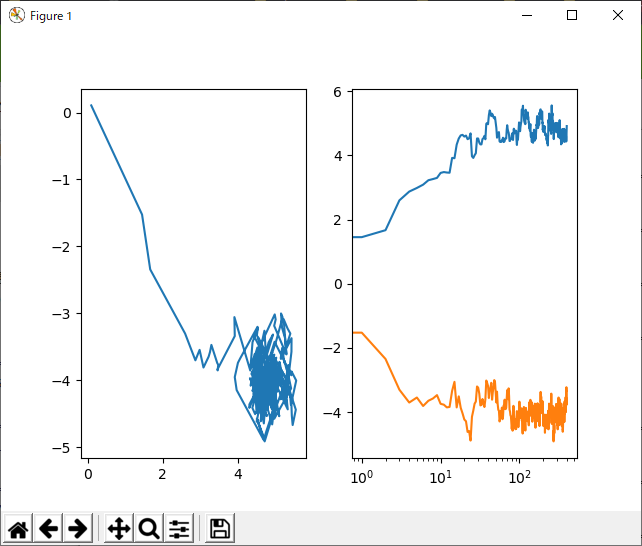
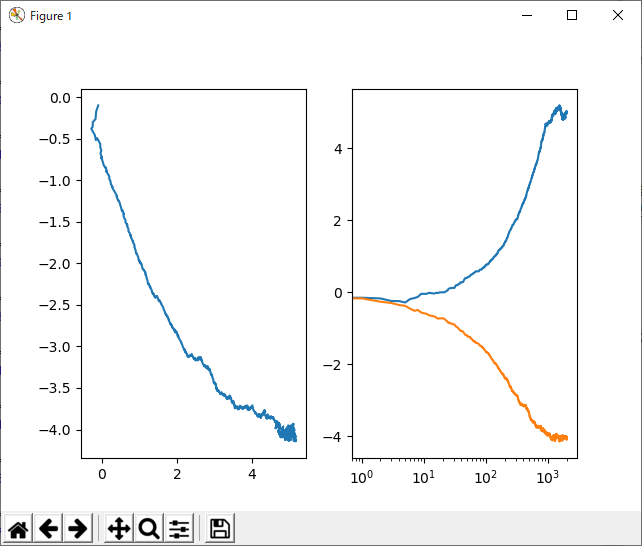
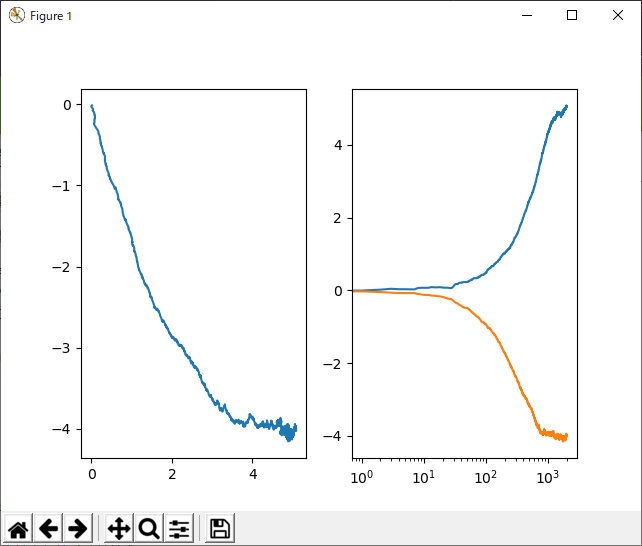
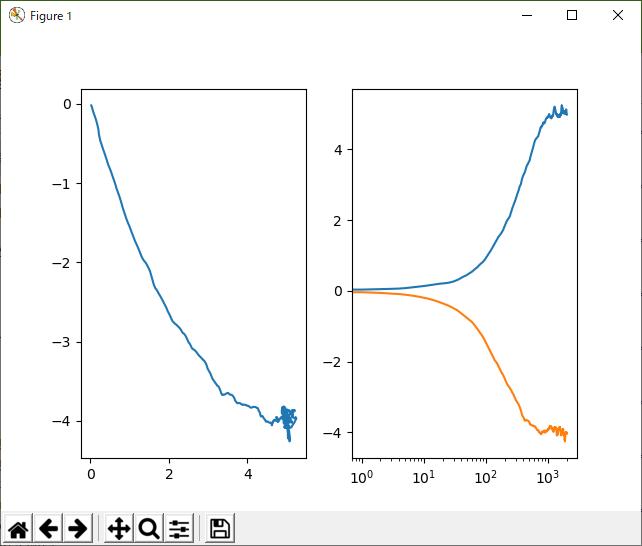
おもむろにこのコードを走らせると、得られるのがこれだ!
例によって、格好つけてX軸は対数だぜ。左のグラフが縦軸にパラメータb横軸にパラメータaを取ったもので、右のグラフが、パラメータaとパラメータbの変化をそれぞれプロットしたもの。なんか、うにょうにょーって感じでパラメータが収束してますな。どれどれ。
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 5.00185944 -3.94859574]
>>>
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 5.12171416 -4.02644124]
>>>
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 4.90653372 -3.82161245]
>>>
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 5.01539247 -3.98697468]
>>>
分散1の正規分布からノイズを乗せているにしては、良い方?なのかなぁ。ただデータ数が結構あるからね。データを減らしてみよう(1000→400)
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 4.63100686 -4.23340308]
>>>
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 4.77784148 -4.07638642]
>>>
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 4.52422703 -4.06309402]
>>>
============= RESTART: D:/Project/python/finance/tstools/sgd.py =============
[ 4.65238286 -3.85758399]
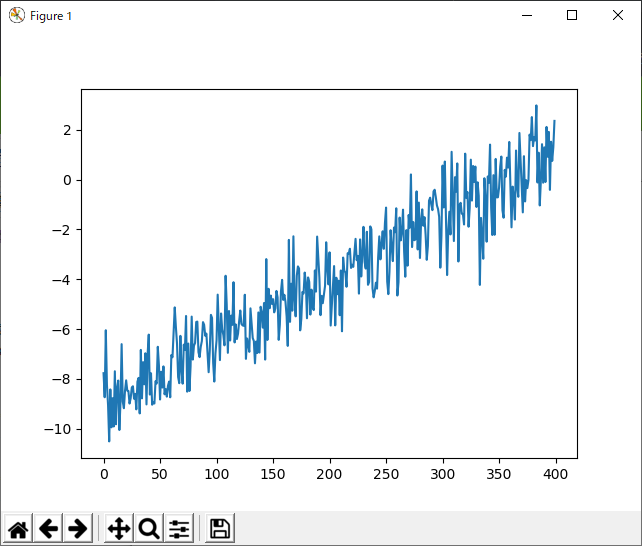
あー、結構ばらつくね。結構だわ。あれ、これもしかしてノイズに弱い?どうだろう?普通に、ペナルティかけて線形回帰とかしたら、もっと安定しそうな気がする。少ないとはいえ400点だからね。でも、これは無印のSGDなので、こんなもんでも仕方がない。ちなみに、データ自体を図示するとこんな感じ。
言うほどノイジーでもないか。まぁ、こんなもんです。
学習率
さて、素のSGDのパラメータは、一個!素晴らしい。ということで、その一個(学習率)をいじってみましょう。デフォルトのα=0.01からα=0.1に変更してみたいと思います。
ようするに、収束に必要な時間は短くなるけど、収束後のパラメータの分散が大きくなると、まぁ、そんな感じ。予想通りといえば、予想通りですな!というわけで、反復と共にこの学習率を小さくするような工夫をすれば、もっと良くなりそう(たしかそれがAdam)
Momentum
まず、SGDに対する最も簡単な改良を行ってみる。その名もモーメンタム(ここでエコー…いや、エコーかけるほどのものではないか)。普通なら、ここで数式を見ながら、講釈をたれるのだろうが、面倒なので実装から。
def sgd3(grad, xs, w, alpha, mu):
tr = []
vt = np.zeros(xs.shape[1])
for x in xs:
vt = mu * vt + grad(x, w)
w = w - alpha * vt
tr.append(w)
return w, tr
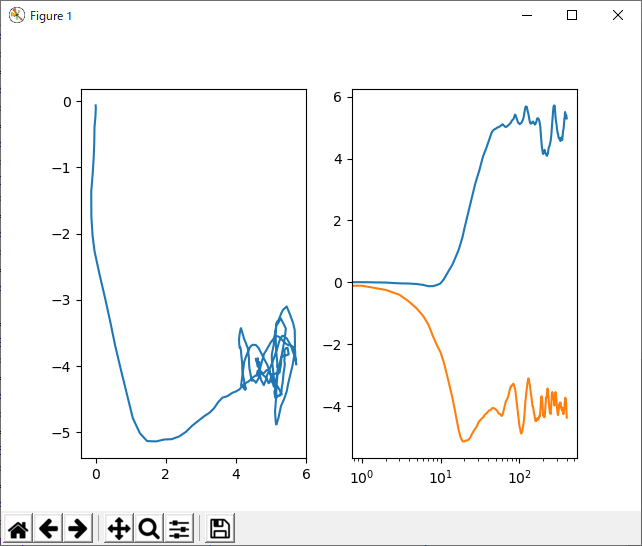
変わったのは、vtという要素が増えたことですな!このvtってのはいわゆる慣性のような働きをするらしい。そうかなぁ…慣性には見えないな。どっちかって言うと、勾配の指数平均を取っているような感じに見えるね。でも、まぁ、これで性能が向上するらしい。学習率α=0.01、モメンタム0.9にして効果を見てみる。
滑らかになったね!パラメータの動きが!ただ、これホントにうれしいのかなぁ。
AdaGrad
というわけで、次は有名どころAdaGrad。
def ada(grad, xs, w, eta0=0.001, eps=1e-8):
tr = []
h = np.ones(xs.shape[1]) * eps
for x in xs:
g = grad(x, w)
h = h + g * g
eta = eta0 / np.sqrt(h)
w = w - eta * g
tr.append(w)
return w, tr
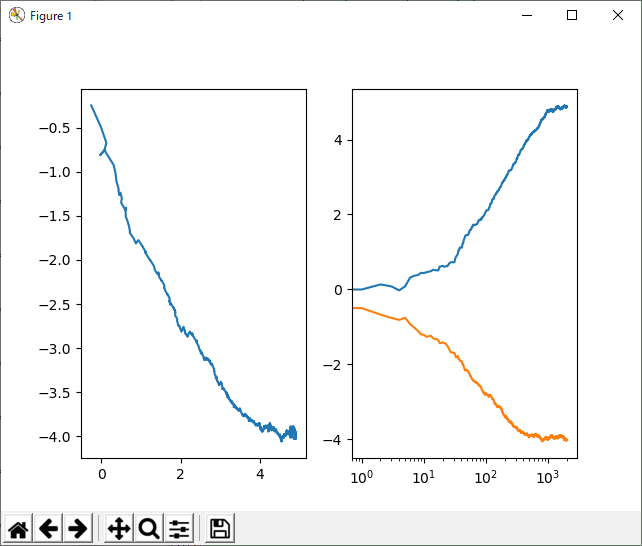
パラメータはeta0 = 0.25、eps=0.01本来は、eta0=0.01、eps=1e-8とかのオーダーらしいのだが、今回の問題では、それじゃ全然収束する気配がなかったので、パラメータ変更。また、データ数も二倍に増やした。
前の二つに比べてゆーっくり動く感じである。ただ、安定性(?)はよさそうかも。あんまりバタバタしない感じ。
RMStop
AdaGradの改良バージョンらしい。
def rmstop(grad, xs, w, eta0=0.01, alpha=0.99, eps=1e-8):
tr = []
h = np.zeros(xs.shape[1])
for x in xs:
g = grad(x, w)
h = alpha*h + (1-alpha)*g*g
eta = eta0 / (np.sqrt(h) + eps)
w = w - eta * g
tr.append(w)
return w, tr
いや、こんなもん、片っ端から実装しても時間の無駄にしかならんのは分かってるんだけどさ。いやね、どんどんパラメータが増えてませんか??一応、こういうアルゴリズムも種々の「ろんぶん」などで提案されたものであり、そこそこの根拠があるのは分かってるんだけどさ。そんなに変わんねーって、こんな小手先のチューニングしたところでさ。
ね。問題による、っていう人もいるけど、ほんとそうかなぁ。一般的に言う「問題による」というより、「このアルゴリズムを開発した人の問題」にたいして最適化されてるだけじゃないのかなぁ。たいして違いねーもん。
AdaDelta
たいしていうことはないぜ!
def adadelta(grad, xs, w, rho=0.95, eps=10e-6):
tr = []
h = np.zeros(xs.shape[1])
s = np.zeros(xs.shape[1])
for x in xs:
g = grad(x,w)
h = rho*h + (1-rho)*g*g
v = g*np.sqrt(s+eps)/np.sqrt(h+eps)
s = rho*s + (1-rho)*v*v
w = w - v
tr.append(w)
return w, tr
じゃっかん、なめらか。ただ、乱数のあたり目とかもあるからなぁ。AdaGrad以降はあんまり変化がない気がします。
Adam
これが一時、ディープラーニング、ディープラーニングとか言ってる人たちの間で話題になってたよね!高性能みたいな。
def adam(grad, xs, w, alpha=0.02, beta1=0.9, beta2=0.999, eps=10e-8):
tr = []
m = np.zeros(xs.shape[1])
v = np.zeros(xs.shape[1])
for x, t in zip(xs, range(len(xs))):
g = grad(x,w)
m = beta1*m + (1-beta1)*g
v = beta2*v + (1-beta2)*g*g
m_hat = m / (1-pow(beta1,t+1))
v_hat = v / (1-pow(beta2,t+1))
w = w - alpha*m_hat/(np.sqrt(v_hat)+eps)
tr.append(w)
return w, tr
ちょっと自信がないんだけど、m_hatとかv_hatの更新のところ、分母は累乗でいいんだよね!?一応「ろんぶん」も観てみたんだけど、指数的に減衰って書かれてたから、これでいいと思うんだけど。beta1なんでステップ数進んだらほとんど、ずーっと1のまんまですぜ。いやね、パラメータ増やしたからって性能上がるかなぁ。一応、二次モーメントまで見てるから、どうのという理屈が書かれていたけど、そもそもさ、パラメータ数がアホみたいに多い最適化アルゴリズムってのもね。それって、性能悪いってことじゃないのぉ?だって、あれこれいじらないとダメなんでしょ?性能のいいアルゴリズムなら、あれこれいじらなくともバシッと最適化できるでしょ(謎のdisり)。
なめらか。ただ、推定結果や収束時間がAdaGradにくらべてそれほどいいとは思わない。これって、滑らかだといいことあるのかな?ニューラルネットとかを学習する場合。あれって、誤差がどんどん伝播していくから、「なめらか」なほうがいいとかあるのかもしれないね。知らんけど。
結論
一時期話題になったSGDのいろいろなアルゴリズムをやってみた。
- SGD、Momentum、AdaGradは全然違う。
- RMStop、AdamとかはAdaGradを滑らかにしたやつ。
- 線形回帰というアホ単純な問題であればAdaGrad以降はあまり違いなし。
というわけで、ディープラーニングとかはともかく、SGDを単なる最適化目的で使うのであれば、なんとか、みたいなアルゴリズムはなくてもいいみたい。普通にやればできる。ただし、話題になった系のやつらは、どうも収束までの経路を「なめらか」にしようと頑張っているように見える。もしかすると、ディープラーニングなどの場合、こういうノイズのない感じに収束していく方がいいとか、あるのかもしれない。
以上です。