運搬経路問題（配送最適化問題，Vehicle Routing Problem) をPuLPで解く

巡回セールスマン問題を一般化した問題である「運搬経路問題」を，最適化問題を簡単に実装できるライブラリであるPythonの「PuLP」を使って解いてみました．

運搬経路問題(VRP)を解く　混合整数計画編 を参考にさせて頂きました．

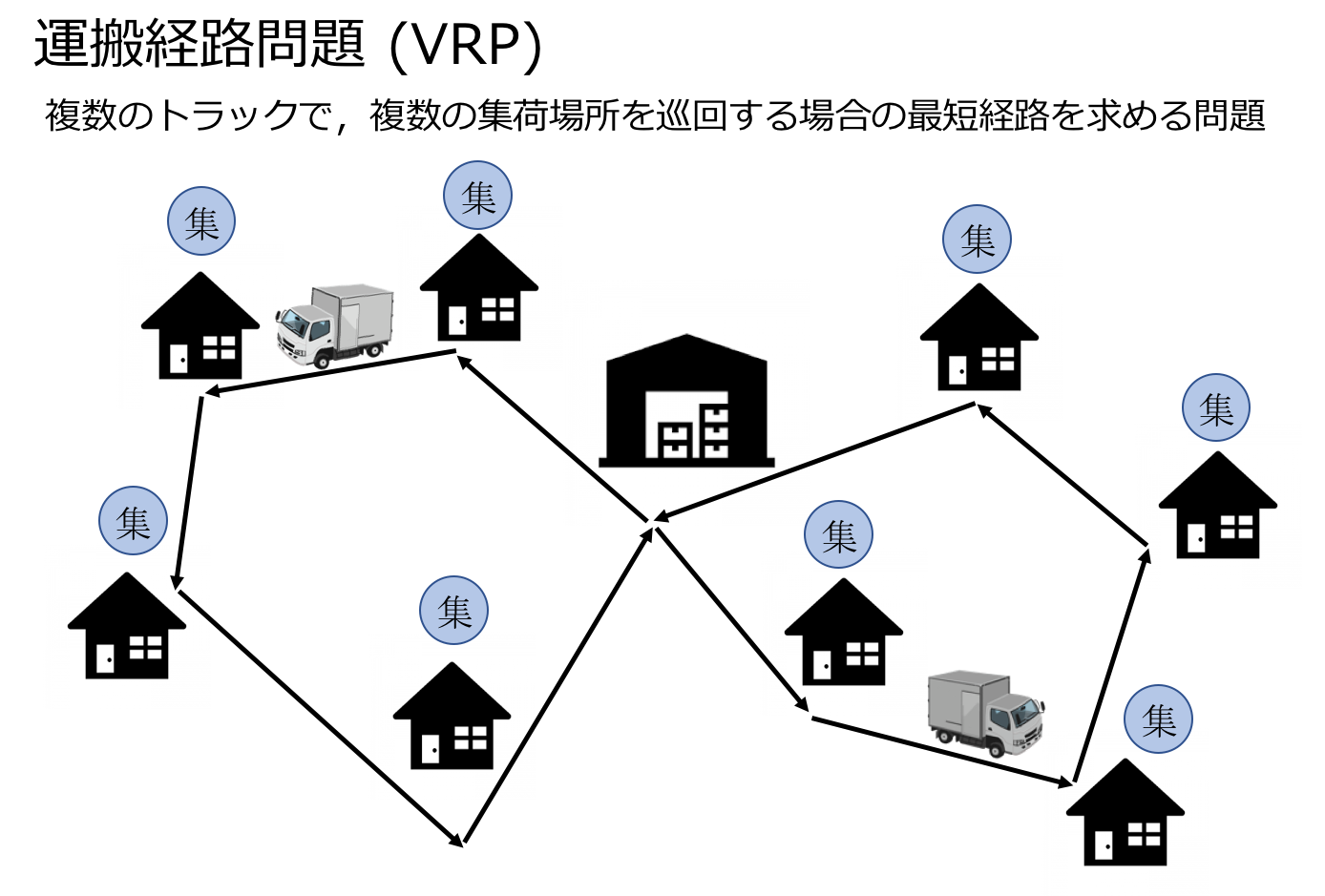
#運搬経路問題 (VRP)とは
運搬経路問題は，複数の車両で複数の顧客のいる場所に訪れ，荷物の集荷or配達をするときに，その移動コストを最小化するような経路を求める問題です． Vehicle Routing Problem (VRP)や車両配送問題，配送最適化問題とも呼ばれます．

車両が一つで車両の容量や時間の制約が無い場合は，巡回セールスマン問題と同じです．なお，訪れる顧客を予めクラスタリングして，クラスタ毎に巡回セールスマン問題を解くことで，全ての顧客を最小コストで訪れる経路を求める方法（クラスター先・ルート後法）や，最初に全ての顧客を対象に巡回セールスマン問題を解いた後で，それらをクラスタリングする方法（ルート先・クラスター後法）もあります．

VRP研究

1959年にGeorge DantzigによってVRPが定義されました．George Dantzigは，線形計画法の一つである単体法の提案や，アメリカの49都市の巡回セールスマン問題を解いたことで有名な数学者です．その後，1964年にClarkeとWrightがセービング法（効率的な貪欲法）というDantigらの手法を改良したものを提案したり，1970年代にMITでWilsonらが人の送迎を行う場合のVRP (DARP)の研究に発展させたり，より複雑な問題設定や定式化，それを解くアルゴリズムの提案がされています．

VRPの種類・派生

VRPは制約の有無や問題設定によって次のような分類がされています．

略称	名称	制約・問題設定
CVRP	Capacitated VRP	車両に載せることができる荷物の容量の制約付き
VRPTW	VRP with Time Windows	何時から何時の間に集荷or配達して欲しいという顧客の希望の時間帯の制約付き
DCVRP	Distance Constrained VRP	車両が走行できる距離の制約付き
HVRP	Heterogeneous fleet VRP	車両の種類が異なる場合のVRP
MDVRP	Multi Depots VRP	車両が出発・到着する車両倉庫(depot)が複数ある場合のVRP
VRPB	VRP with Backhaul	車両に載せている荷物を全て配達し終わった後に，集荷に向かう場合のVRP
VRPPD	VRP with Pick-up and Delivery	集荷および配達を行う場合のVRP．荷物の集荷が配達より先という制約が付く．
PDP	Pick-up and Delivery Problem	VRPPDと同じような問題設定で，荷物の特性1で区別されることがありますが，定義はあいまい．
DARP	Dial a Ride Problem	運ぶのが人の場合のPDP．オンデマンド型交通の配送最適化問題．人の移動時間についての制約や目的関数が追加される．

今回は，容量制約付きの運搬経路問題，CVRPを実装します．
#CVRPの定式化

問題

複数の車両で複数の顧客のいる場所に訪れ，荷物の集荷をするときに，その移動コストを最小化するような経路を求めよ.なお，集荷する荷物の量が車両の容量を超えてはいけない．

記号の説明

• $G=(V,E)$：顧客の場所および経路を表すグラフ．（ここでは無向グラフ）
• $V=\{0,1,...,n\}$：ノードの集合．depot（車両の倉庫）を表すノード$0$と各顧客を表すノード$\{1,...,n\}$から成る．
• $E$：各ノード間を結ぶエッジ$e_{ij}=(i,j)$の集合
• $K=\{1,2,...,|K|\}$：車両の集合
• $d_i(\geqq0)$：各顧客$i$の荷物の量
• $Q(\geqq0)$：各車両$k \in K$の最大容量
• $c_{ij}$：顧客$i$と$j$間の移動コスト（ここでは直線距離）

決定変数

ここで知りたいのは，車両$k$が経路$e_{ij}$を通るかどうかなので，決定変数を次のように定義します．

x_{ij}^{k} = \left\{
\begin{array}{ll}
1 & (車両kが経路e_{ij}を通るとき) \\
0 & (それ以外)
\end{array}
\right.

目的関数

全ての車両の移動コストの総和⇒最小化

制約

• 各顧客の場所に訪れるのは1台の車両で1度
• depotから出発して，depotに戻ってくる
• 車両の最大容量を超えてはいけない

これを踏まえて，CVRPを次のように定式化します．

Min \sum_{k\in K} \sum_{(i,j)\in E}c_{ij} x_{ij}^k \tag{1}

subject to

\sum_{k \in K} \sum_{i \in V, i \neq j} x_{i j}^{k}=1  \qquad \qquad \forall j \in V \setminus \{0\} \tag{2} 

\sum_{j \in V \setminus \{0\}} x_{0j}^{k}=1 \qquad \qquad \forall k \in K \tag{3} 

\sum_{i \in V, i \neq j}x_{ij}^{k} - \sum_{i \in V} x_{ji}^{k} =0 \qquad \qquad \forall j \in V, \forall k \in K \tag{4} 

\sum_{i \in V} \sum_{j \in V \setminus \\{0\\}, i \neq j} q_{j} x_{i j}^{k} \leq Q \qquad \qquad  \forall k \in K \tag{5} 

\sum_{k \in V} \sum_{(i,j) \in E, i \neq j} x_{ij}^{k} \leq |S| - 1  \qquad \qquad  S \subseteq V \setminus \{0\} \tag{6} 

x_{i j}^{k} \in\{0,1\} \qquad \qquad  \forall k \in K, \forall(i, j) \in E \tag{7}

(1)式は，目的関数である全車両の移動コストを最小化することを表しています．
(2)式は，各顧客の場所に訪れるのは1台の車両で1度であるという制約．(3)式はdepotから出発するという制約．(4)式はある顧客の場所に来る車両数と出る車両数が同じであるという制約．(5)式は各車両において容量が超えないようにする制約です．(6)式はdepotから繋がれていない経路を除去するための制約（部分巡回路除去制約）です．(7)式は決定変数の制約です．

部分巡回路除去制約とは，下図のような部分巡回路を除去するための制約です．巡回セールスマン問題の制約としても使われます．（藤江哲也先生のスライド 整数計画法チュートリアル：モデリングと解法から引用）

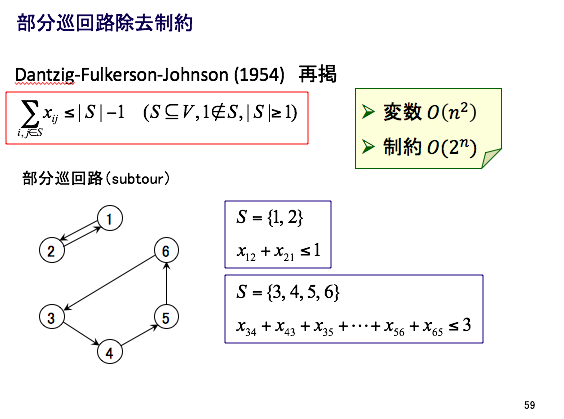
部分巡回路除去制約は様々な方法（他に有名なのはMTZ制約）が提案されていますが，今回はこのスライドのDFJ(Dantzig-Fulkerson-Johnson)制約を用います．
depotを含まないノード$\{1,...,n\}$の組合せからなる集合$S$定義します．そのようなノードからなる部分巡回路を車両が通るとき，制約不等式の左辺が，右辺（$|S|$-1）よりも大きくなります．これを用いて部分巡回路を除去します．

実装

インプット

まず，顧客の位置や荷物の量，車両数などのデータを作成します．（追記：コスト計算の部分を修正しました．2022/3/36）

import numpy as np
import pandas as pd
import pulp
from scipy.spatial import distance_matrix
import itertools
import matplotlib.pyplot as plt
%matplotlib inline #Jupyterの場合

customer_count = 10 #顧客数（id=0はdepot）
vehicle_count = 4 #車両数
vehicle_capacity = 50 #車両容量

np.random.seed(seed=32)

#各顧客のx,y座標をDataFrameとして作成
df = pd.DataFrame({"x":np.random.randint(0,100, customer_count), 
                   "y":np.random.randint(0, 100, customer_count), 
                   "demand":np.random.randint(5, 20, customer_count)})

#id=0はdepotなので，demand=0にする
df.iloc[0].x = 50
df.iloc[0].y = 50
df.iloc[0].demand = 0

#コストとしてノード間の直線距離を求める

#修正前
#cost = pd.DataFrame(distance_matrix(df.values, df.values), index=df.index, columns=df.index).values
#修正後
cost = pd.DataFrame(distance_matrix(df.loc[:,["x","y"]].values, df.loc[:,["x","y"]].values), index=df.index, columns=df.index).values

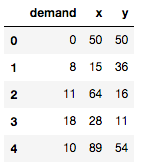
df.head()

各顧客の位置と荷物量(deamand)は，こんな感じになります．

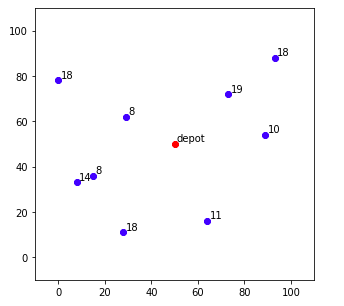
# depotと顧客の位置の可視化．添え字は荷物の量
plt.figure(figsize=(5,5))
for i in range(customer_count):    
    if i == 0:
        plt.scatter(df.x[i], df.y[i], c='r')
        plt.text(df.x[i]+1, df.y[i]+1, "depot")
    else:
        plt.scatter(df.x[i], df.y[i], c='b')
        plt.text(df.x[i]+1, df.y[i]+1, str(df.demand[i]))
plt.xlim([-10, 110])
plt.ylim([-10, 110])

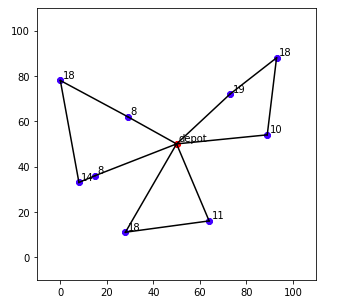
depotと顧客の位置の可視化を可視化したものです．添え字は荷物量です．

定式化＆解計算

上記の定式化を，最適化問題を簡単にモデリングできるライブラリ「PuLP」を用いて実装します．必要な車両数は少ないほうが良いので，最適解が出たら終了するようにしました．

for vehicle_count in range(1,vehicle_count+1):
    # 問題の宣言
    problem = pulp.LpProblem("CVRP", pulp.LpMinimize)

    # 決定変数
    x = [[[pulp.LpVariable("x%s_%s,%s"%(i,j,k), cat="Binary") if i != j else None for k in range(vehicle_count)]for j in range(customer_count)] for i in range(customer_count)]

    # 目的関数
    problem += pulp.lpSum(cost[i][j] * x[i][j][k] if i != j else 0
                          for k in range(vehicle_count) for j in range(customer_count) for i in range (customer_count))

    # 制約
    # (2)式，各顧客の場所に訪れるのは1台の車両で1度である
    for j in range(1, customer_count):
        problem += pulp.lpSum(x[i][j][k] if i != j else 0 for i in range(customer_count) for k in range(vehicle_count)) == 1 

    #(3)式, depotから出発して，depotに戻ってくる
    for k in range(vehicle_count):
        # デポを出発した運搬車が必ず 1つの顧客から訪問を開始することを保証する制約条件
        problem += pulp.lpSum(x[0][j][k] for j in range(1,customer_count)) == 1
        # 必ず 1 つの顧客から運搬車がデポへ到着すること保証する制約条件
        problem += pulp.lpSum(x[i][0][k] for i in range(1,customer_count)) == 1

    #(4)式, ある顧客の所に来る車両数と出る車両数が同じ
    for k in range(vehicle_count):
        for j in range(customer_count):
            problem += pulp.lpSum(x[i][j][k] if i != j else 0 for i in range(customer_count)) -  pulp.lpSum(x[j][i][k] for i in range(customer_count)) == 0

    #(5)式, 各車両において最大容量を超えない
    for k in range(vehicle_count):
        problem += pulp.lpSum(df.demand[j] * x[i][j][k] if i != j else 0 for i in range(customer_count) for j in range (1,customer_count)) <= vehicle_capacity 


    #(6)式, 部分巡回路除去制約
    subtours = []
    for i in range(2,customer_count):
         subtours += itertools.combinations(range(1,customer_count), i)

    for s in subtours:
        problem += pulp.lpSum(x[i][j][k] if i !=j else 0 for i, j in itertools.permutations(s,2) for k in range(vehicle_count)) <= len(s) - 1
    
    #最適化問題を解く
    #最適解が出たら終了
    if problem.solve() == 1:
        print('車両数:', vehicle_count)
        print('目的関数値:', pulp.value(problem.objective))
        break

車両数: 3
目的関数値: 416.15357538029696

となったので，全顧客をまわるのに車両が3台必要であることがわかりました．

結果の可視化

最適化された車両の経路を可視化します．

plt.figure(figsize=(5,5))
for i in range(customer_count):    
    if i == 0:
        plt.scatter(df.x[i], df.y[i], c='r')
        plt.text(df.x[i]+1, df.y[i]+1, str(i)+",depot")
    else:
        plt.scatter(df.x[i], df.y[i], c='b')
        plt.text(df.x[i]+1, df.y[i]+1, str(i)+"("+str(df.demand[i])+")")
plt.xlim([-10, 110])
plt.ylim([-10, 110])

for k in range(vehicle_count):
    for i in range(customer_count):
        for j in range(customer_count):
            if i != j and pulp.value(x[i][j][k]) == 1:
                plt.plot([df.x[i], df.x[j]], [df.y[i], df.y[j]], c="black")

このようになりました．

まとめ

今回は，容量制約付き「運搬経路問題」の定式化と，「PuLP」を使った実装について紹介しました．今後は，より複雑な制約や条件の問題についても理解・実装していきたいと思っています．

参考

• 物流における最適化問題
• 運搬経路問題(VRP)を解く　混合整数計画編
• [容量制約有りの配送計画問題(CVRP)を量子アニーリングで解く] (https://qiita.com/snhrhdt/items/d69e6b2dae5d4b439563)
• [A Review of Dynamic Vehicle Routing
  Problems] (https://www.researchgate.net/publication/257196300_A_review_of_dynamic_vehicle_routing_problems)
• Two models of the capacitated vehicle routing problem
• 整数計画法チュートリアル：モデリングと解法

1. 荷物がお金の場合，集荷は1,000円で，配達は700円のようにペアになってなくて良いですが，通常は集荷した荷物をそのまま配達するのでペアになっています．PDPは集荷・配達がペアになっているという問題設定が多いです． ↩