QunaSysでインターンを行っているヒデトです。
今回は「容量制約有りの配送計画問題(以下CVRP)を量子アニーリングで解いた」という論文を読んだのでそれについてまとめたいと思います。
読んだ論文
[1] A Hybrid Solution Method for the Capacitated Vehicle Routing Problem Using a Quantum Annealer
https://arxiv.org/abs/1811.07403
前回まとめた、交通最適化と同様にVolkswagenが行った研究論文になります。
概要
概要はCVRPを古典と量子のハイブリッドで解いたというものになります。
どこに量子アニーリングを使うかというと、古典コンピュータでCVRPを複数の巡回セールスマン問題(TSP)に帰着させ、TSPを量子アニーリングを用いて解いています。
論文の内容としては、まずCVRPのどこに量子アニーリングを使うかを議論し定式化を行い、実際にベンチマーク問題で結果の比較を行っています。
前回のVolkswagenの論文と比べて
1.問題設定が現実問題に大きく近づいた
2.通常のPCで解かれた最新の結果と比較している
という2点で以前の交通最適化より大分進歩していると感じました。
CVRPとは
CVRPという問題について説明します。
配送計画問題(VRP)とは、荷物の集積所(デポ)から各顧客へトラックで荷物を届ける際に、なるべくコスト(時間や距離)を小さくするようなトラックのルートを見つける問題です。
この問題は、巡回セールスマン問題の一般化に当たります。つまり、トラック1台かつ1つのルートで全ての顧客を回るという特殊ケースが巡回セールスマン問題に当たります。
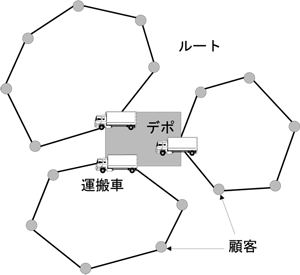
*ORwikiより
このVRPにおいて、トラックの容量(一度にトラックに荷物を詰められる上限)が決まっている際、容量制約有り配送計画問題(CVRP)と呼びます。
このCVRPはNP困難という解くのが難しい問題に分類されます。
CVRPのインプットとして、頂点(V)と枝(E)からなるグラフ$G=(V,E)$が与えられます。
頂点集合$V= \{ 1,....,n \}$は、デポと訪問する顧客を表しています。頂点1がトラックが出発・到着するデポです。
枝$(i,j)\in E$には、非負のコスト$c_{ij}$がついており、これは現実における顧客$i$から顧客$j$までの距離などに対応します。
また、それぞれの顧客は異なる需要量$q$を持っており、トラックでデポからトラックの最大容量$Q$を超えないように、配達しなくては行けません。
与えられるグラフは通常完全グラフです。すなわち、どの頂点間も行き来が可能というように問題設定されています。
求めるもの(アウトプット)は、総コストがなくべく小さくなるような、それぞれのトラックのルートです。
今回のトラックは区別がなく、全てのトラックは同じ最大容量$Q$を持っています。
本論文はこのCVRPに関するものになっています。
量子アニーリングを用いたアルゴリズム
VRPに関する研究は現在盛んに行われており、様々な解の求め方(アルゴリズム)が提案されています。
NP困難な問題なので、通常ヒューリスティックなアルゴリズムを使用します。
今回は、2-Phase-Heuristicsという古典コンピュータでも使われているアルゴリズムを使います。これはどういうものかというと、以下の2段階より答えを求めます。
1.距離が近い同士の頂点をトラックの最大容量$Q$を超えないようにまとめます(クラスタリング、下の図b)
2.クラスタリングされた頂点集合内で、コストが最小となるようなルートを求めます(巡回セールスマン問題、下の図c)
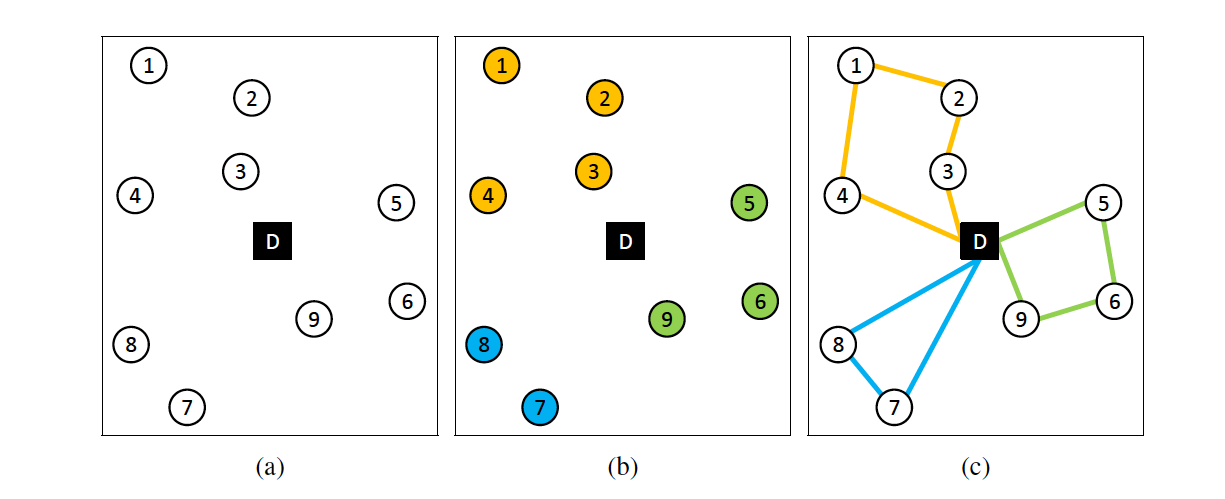
*1より
1のクラスタリングはナップザック問題(KP)になります。
一つのクラスターにトラックの最大容量$Q$を超えないように、なるべく多くの近い頂点を入れていくといった具合です。
2で、その一つのクラスター内でコスト最小のルートを求めます。
これは巡回セールスマン問題(TSP)になります。
この時以下の図のようにアニーリングの使いどころに関して、3つのパターンに分けてみます。
(1)ナップザック問題(KP)と巡回セールスマン問題(TSP)を別々に量子アニーリングで解く(下図の左)
(2)KPとTSPを同時に量子アニーリングで解く(下図の真ん中)
(3)KPは古典的に解き、TSPは量子アニーリングで解く(下図の右)
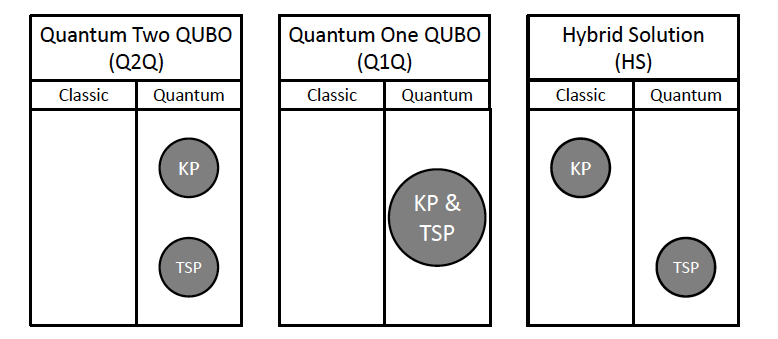
*1より
今回の論文によると、(1)と(2)は上手くいかなかったそうですが、あまり詳しくは言及されていませんでした。
(1)は、KPを量子アニーリングで解くのが難しいみたいです。
近い頂点同士をクラスタリングするので、枝のコスト$c_{ij}$が非常に小さいもの同士のQUBOにおけるパラメーター調整が難しいようです。
(2)ではKPとTSPがお互いを邪魔し合ってしまいます。
というのも目的関数がKPに関するものとTSPに関するものと2つ存在するため、実行可能だけれどもコストの大きいルート、実行不能でコストの小さいルートが出てきてしまうそうです。
ということで今回は
(3)KPは古典コンピュータ、TSPは量子アニーリング
を採用しています。
Phase 1 - クラスタリング
クラスタリングは古典コンピュータを用いて、以下の手順で行います。
① 1つの頂点を選ぶ
② クラスタリングされた顧客の需用量$q$の総和がトラックの最大容量$Q$を超えるまで、近くの頂点をクラスタリングする
③ あるクラスター内の頂点を別の頂点に移動させてみてる
もう少し詳細に見て行きます。
①で、まず1つの頂点を選びます。この1つの頂点をどう選ぶかというと、デポから一番遠い距離にある頂点や一番需用量$q$が大きい頂点を選びます。
これらの頂点を最初に選ぶ理由は、経験的にこれらの頂点が問題に与える影響が大きいということで、確固たる理由がある訳ではありません。
②では、①で選んだ頂点の周りの点をクラスタリングしていきます。近くの点の基準は、これまでクラスタリングされた頂点の中間地点から一番距離が近い点です。
よって、以下のように中間地点(座標)を定義します。
$$
CC(m_k) =
\left(
\sum^n_{i=0} \frac{v_{i}^x}{n} , \sum^n_{i=0} \frac{v_{i}^y}{n}
\right)
$$
$m_{k}$はk番目のクラスター、$v_{i}^x,v_{i}^y$は$i$番目にクラスタリングされた頂点の$x$座標及び$y$座標です。また、ここでの$n$は、$m_{k}$にクラスタリングされた頂点の個数です。
一通りクラスタリングが終わったら、③でクラスター内の頂点を入れ替えて改善を行います。
$u \in m_{k}$の頂点を$m_{j}$に入れてみて、 容量$Q$を超えないかつ$CC(m_{j})$から$u$の距離が$CC(m_{k})$の距離よりも小さくなれば、$u \in m_{j}$とします。
これを所定の回数行い、改善を行います。
Phase 2 - ルーティング
Phase1のクラスタリングが終わったら、1つのクラスター内でコスト最小のルートを求めます。
これは先にも述べた通りそれぞれが量子アニーリングよく解かれている、巡回セールスマン問題(TSP)になります。
ということでTSPを量子アニーリングが解けるQUBOの形に定式化します。
そのために以下の変数を用意しましょう。
$$
x_{ij}=
\left\{
\begin{array}{}
1 & ( 頂点i をj番目に訪問する時) \
0 & ( それ以外)
\end{array}
\right.
$$
このように変数を用意すれば、目的関数のコスト関数は1番目に訪問する頂点から、$n$番目に訪問する頂点までの枝に張られた重み$c_{ij}$の和になります。
よって、コスト関数は以下のようになります。
$$
H_{cost} = \lambda \sum_{j=1} ^n c_{ui} x_{u,j}x_{i,j+1}
$$
$\lambda$はコスト関数とペナルティー関数の重みを調整するパラメーターです。
次に制約条件をペナルティー関数として目的関数に入れます。
今回の制約は、以下の2つですね。
① 1度に訪れられる頂点は1つのみ
② 全ての頂点は必ず1度ずつ訪れなくてはいけない
①を式で表すと
$$
\sum _ {j=1}^n x_{i,j} = 1
$$
②を式で表すと
$$
\sum _ {i=1} x_{i,j} = 1
$$
全ての頂点、全ての順番に対して、これらの制約を破った時に目的関数が大きくなるようにペナルティー関数を以下のようにします。
$$
H_{penalty} = \mu \sum_{i=1}^n
\left(
1- \sum_{j=1}^n x_{i,j}
\right)^2
+
\mu \sum_{j=1}^n
\left(
1- \sum_{i=1}^n x_{ij}
\right)^2
$$
$\mu$は、$\lambda$同様、ペナルティー関数とコスト関数の重みを調整するパラメーターです。
結果
今回は数値実験を実際に行なっています。今回必要なqubit数は頂点の二乗$n^2$になるため、D-waveのqubit数では足りない場合が出てきます。その時は、QBSolveを使って、問題を分割して解いています。
また、TSPとCVRP両方それぞれをベンチマーク問題と比較しています。
巡回セールスマン問題(TSP)の結果
量子アニーリングでの測定を100回行なって、最も良い値と、知られている最も良い値からの偏差を出しています。
また、$\lambda , \mu $のパラメーター調整を250回行なっています。
TSPのみを量子アニーリングで解いた結果が以下のようになっています。
左から、ベンチマーク問題の名前、問題サイズ、知られている最も良い解の値、量子アニーリングの一番良い値、量子アニーリング100回測定の偏差です。
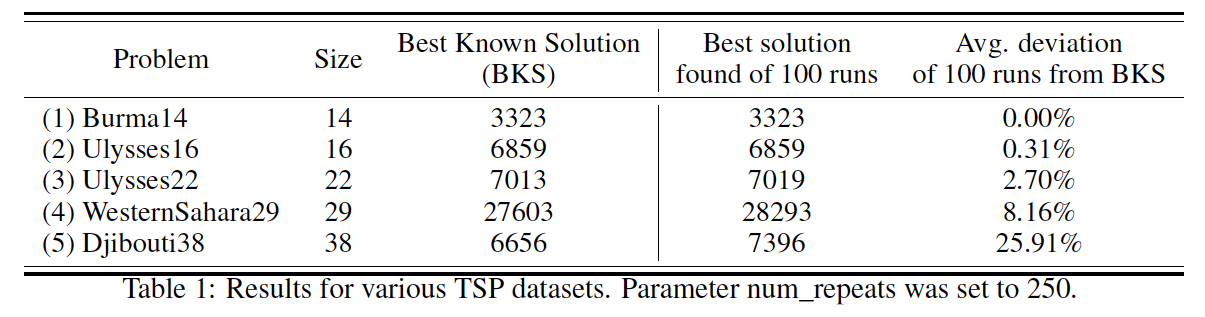
*1より
結果から、問題サイズが小さい時は、最適解が低い偏差で得られていることがわかります。
しかし一方で、問題サイズが大きくなってくると、BKSよりも悪い値しか得られず、偏差も大きくなっています。
また、パラメーター調整を250回より下げてしまうと、より悪い結果が出てくるという結果もありました。
容量制約有り配送計画問題(CVRP)の結果
クラスタリングを古典コンピュータで行い、経路を決定する(TSP)を量子アニーリングで行うというアルゴリズムでCVRPを解いた際の結果を示します。
またクラスタリングの際、どういう基準で最初の頂点を選ぶかというのを、一番遠い頂点を選ぶ(max_distance)と一番需用量の大きい頂点を選ぶ(max_request)と両方行なっています。
左から、ベンチマーク問題の名前、知られている最も良い解の値、max_distanceでクラスタリングを行なった際の量子アニーリングの最も良い値、max_requestでクラスタリングを行なった際の量子アニーリングの最も良い値、max_distanceにおけるBKSと量子アニーリングの偏差、max_requestにおけるBKSと量子アニーリングの偏差です。
ベンチマーク問題の名前の見方ですが、
(用いたデータセット) - n(与えられる頂点数) - k(解くのに必要最低限のトラックの数) という形式で表しています。
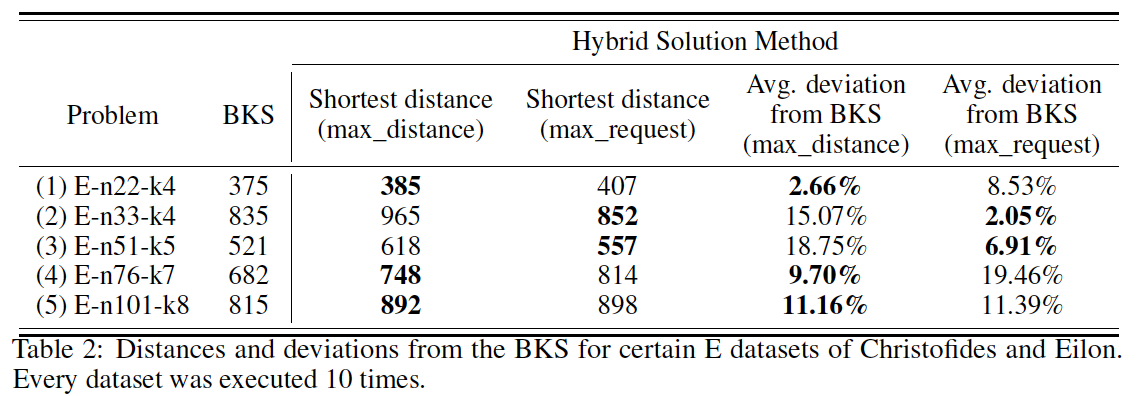
*1より
結果より、最初のクラスタリングのフェーズでmax_distanceかmax_requestかどちらを選んだ方が良いかというのはわからないということがわかります。
次に古典コンピュータのいくつかのアルゴリズムとの比較も行なっています。その結果が次のようになります。
一番右のHybrid Methodが今回アニーリングを用いた結果です。
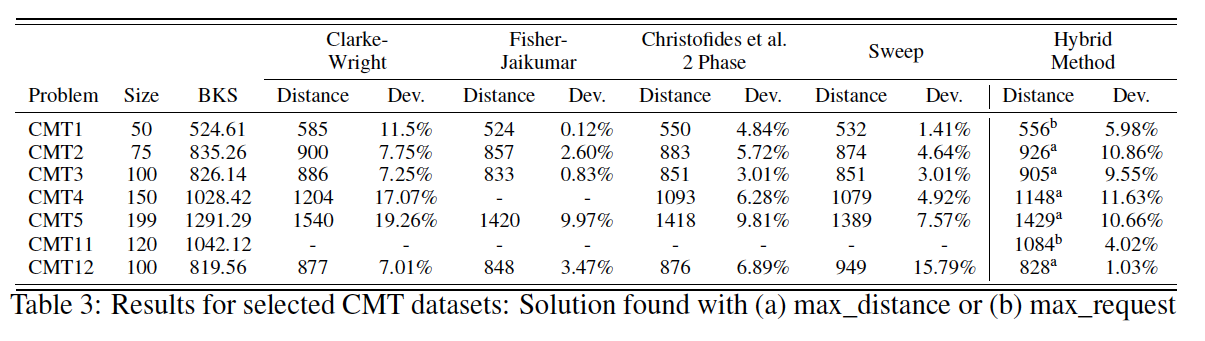
*1より
特出して良い結果という訳でも悪い結果という訳でもないですね。
計算時間に関してですが、上記表の一番目のCMT1についての計算時間の結果が示されています。
古典的なアルゴリズムを用いた際の時間が約1.474秒に対し、量子アニーリング及びQBSolveを用いた計算時間は15.792秒になります。
QBSolveは古典コンピュータを用いており、それと量子アニーリングの通信の時間などに大幅な時間がかかっていると考えられます。
量子アニーリングのみで考えれば、解を得られるのにマイクロセカンドのオーダーで得られます。
考察
言ってしまえば、今回の論文は量子アニーリングで巡回セールスマン問題を解いているだけです。
しかし他に良いアニーリングの使い方があるかと聞かれると確かに頭を悩ませてしまいます。
気になるのが詳しく言及されていなかった、クラスタリングが量子アニーリングで出来なかった理由です。クラスタリングもアニーリングで出来てしまえば、将来的に問題サイズが非常に大きくなった時にとても有利に感じます。
クラスタリングもどうにかアニーリングで出来ないか考えてみると結果がまた変わってくると思いますし、面白いと思います。
また今回の結果ですが、あまりパッとしません。
問題サイズが大きくなると偏差が結構大きくなるのが気になります。量子アニーリングの一つのモチベーションとして、古典コンピュータでは計算時間が莫大になるようなサイズの問題を解きたいというものがあると思います。
しかしこの結果から、推測すると問題サイズが大きくなっても多項式時間で解ける古典のアルゴリズムを越えることは出来ないのではないかという懸念が出てきます。
そしてやはりハードの面がとても重要です。
量子コンピュータが膨大な数のqubitを扱えるようになれば、古典コンピュータとの通信時間もなくなり、マイクロセカンドのオーダーでなんとなく良い解を瞬時に出してくれます。
これは問題サイズが大きくなれば、非常にありがたいものです。
そしてもう一つ重要なのが、制約条件をどうやってつけるかです。
今回は、容量制約しかなかったのでクラスタリングすればどうにかなりましたが、現実世界の配送問題を考えると、時間的な制約は必ずつけなくてはいけません。
これらをどうやって扱うかがこれから重要な問題になってくると思います。