QunaSysでインターンを行っているヒデトです。
今回は量子アニーリングを使って交通最適化を行った論文を読んだので、それについてまとめたいと思います。
読んだ論文
Traffic Flow Optimization Using a Qunatum Annealer
https://arxiv.org/pdf/1708.01625.pdf
VolkswagenがD-Waveと共同で行った研究論文になります。
Quantum Computing at Volkswagen: Traffic Flow Optimization using the D-Wave Quantum Annealer
https://www.dwavesys.com/sites/default/files/VW.pdf
D-Wave作成の、上記論文の発表資料です。具体例がわかりやすいので、これを中心に説明したいと思います。
概要
この研究は 「実社会における問題に対して量子アニーリングを使用する」 というのがモチベーションとなっています。
具体的に何をしたかと言うと、交通流の最適化を量子アニーリングを使って解いています。
交通流を最適化するために行ったのが、「混雑の最小化」です。すなわち、混雑している道路にいる車を、他のルート(道路)へ割り振ることによって混雑を解消しています。
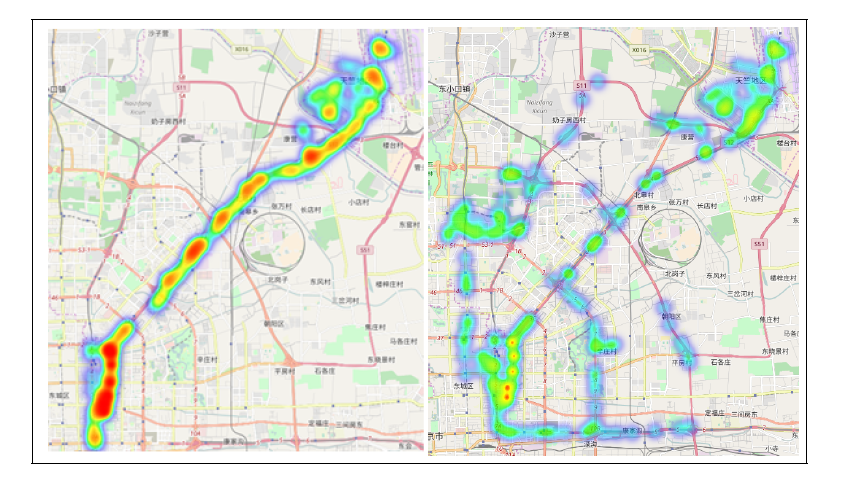
実際に北京の空港と市内を行き来する車について最適化を行った結果が次になります。
左図の状態に今回の最適化を行った結果が右図になります。
内容
今回行った最適化のオーバーフローは以下のようになります。「古典」は古典的な普通なコンピュータによる処理、「量子」は量子アニーリングを使う処理を表します。
- 古典:地図と車のGPSデータを用意
- 古典:混雑が行っているルートを特定
- 古典:それぞれの車に対して、代わりのルートを決定
- 古典:混雑の最小化をQUBOの形に定式化
5. 古典&量子:QUBOの解を見つける(混雑が解消されるような代わりのルートを見つける) - 古典:車のルートを再配置
- 2~6を混雑が解消するまで行う
QUBOについては後述します。
それぞれのステップについて説明していきます。
古典アニーリングでの処理
任意の2地点を繋ぐ道の連なりをルートと言います。
まずPythonのパッケージであるOSMnxを使って、地図を枝(道)と頂点(道と道の繋ぎ目)から成るグラフに変換します。
以下が実際に北京の地図を変換したグラフになります。
そして、T-Drive Trajectoryデータベースにある車のGPSデータを使い、車の現在地に対応するグラフの頂点に車を配置します。
次に、それぞれの車に対して、現在地、目的地、現在試用しているルートを特定します。
全ての車の現在使用しているルートから、混雑している道路を特定します。同じ道路を何台の車を使用するかによって、混雑度を評価しています。
今回は、10台以上が同じ道を使用するとき、混雑している道路と判断しています。
最後にそれぞれの車に対して、現在とは違うルートを2つ決めます。今回は代わりのルートは2つだけですが、2つ以上のルートへの拡張も可能です(変数の数が多くなりますが)。
QUBO(Quadratic Unconstrained Binary Optimization)
量子アニーリングが扱える最適化問題は、2次形式の制約なし0-1変数問題(変数の値が0 or 1)です。実際に式にすると
$$ \boldsymbol{x}^t ・Q・\boldsymbol{x}$$
ここで、$\boldsymbol{x}$はN個の0-1変数ベクトル、tは転置、Qは変数間の関係を表すN×N行列です。アニーリングはこのQUBOを最小化するようなベクトル$\boldsymbol{x}$を求めてくれます。
ここからは、具体例を使って
「0-1変数を使って混雑の最小化問題の定式化」
↓
「上記の問題をQUBOの行列形式に変形」
という形で説明していきます。
最小化問題の定式化
この問題は混雑を最小化する問題です。ですので、混雑表す式を作る必要があります。ここでは、混雑を表す指標として、「同じ道路を何台の車が使用するか」というのを使います。
では式を作るために0-1変数を定義しましょう。
$$
Q_{ij}=
\left\{
\begin{array}{}
1 & ( 車i がルートjを通るとき) \
0 & ( それ以外)
\end{array}
\right.
$$
このように0-1変数を定義すると、最小化する目的関数は以下で表されます。
$$
\sum_{s \in S}
\left(
\sum_i
\sum_j
\sum_{s \in S_{j}}
Q_{ij}
\right)^2
+
K
\sum_i
\left(
\sum_j
Q_{ij}
-1
\right)^2
$$
第一項はコスト関数と言い道路sを通る車の台数の二乗の和、第二項はペナルティー関数と言いそれぞれの車は唯一のルートしか取れないという制約を表しています。
どういうことが具体例を使って説明します。
具体例:車2台の最適化
・車2台がA地点を出発し、B地点に向かうルートについての最適化について考えます。
【目標】
2台の車が通る道がなるべく重複しないようにルートを振り分ける(混雑の最小化)
コスト関数
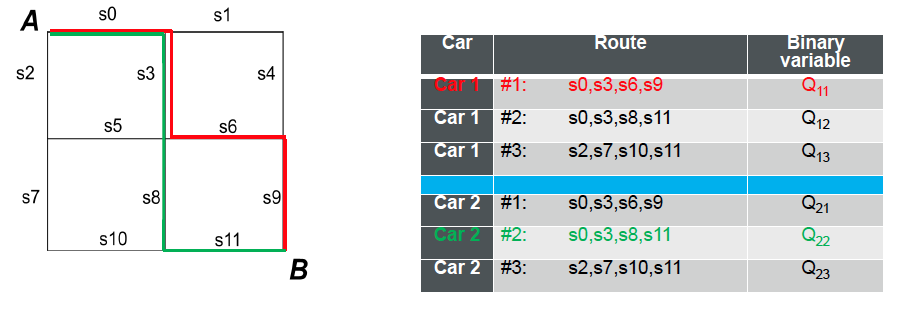
グラフの辺であるsは道を、A→Bへの道の連なりがルートです。今、車1が赤線のルートを、車2が緑線のルートを通っているとします。それぞれの車に対するそれぞれのルートを$Q_{ij}$に割り当てます。
2台の車がどれだけ同じ道を使うかを考えたいので、ある道を使う車の台数の二乗を考えてみましょう。二乗で考えることによって、道が重複している時ほど大きな値をとります。これをコスト関数と名付けます。
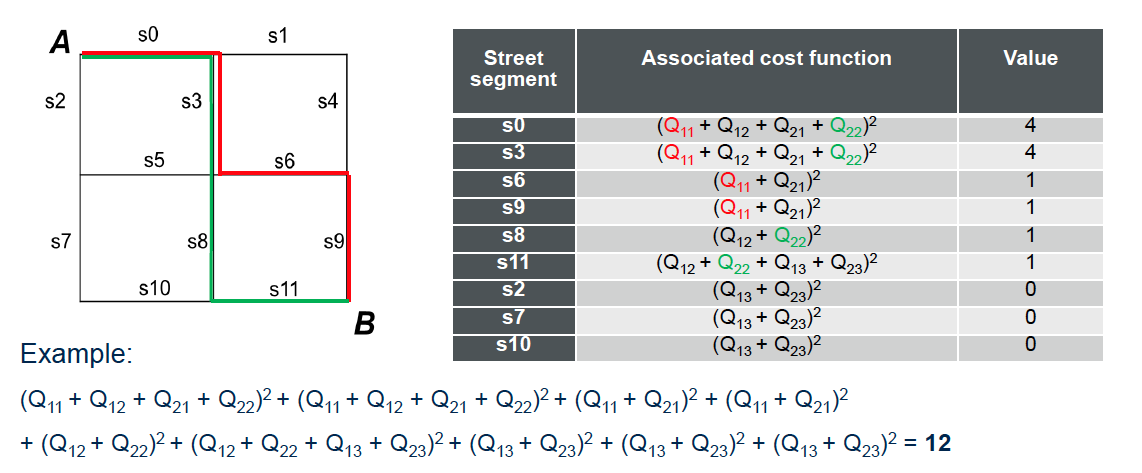
それぞれの道を使用するルートを足して二乗します。実際に現在使用している$Q_{11},Q_{22}$に1を、それ以外に0を代入することによって、今回のコストの総和は12になります。
では2台の車が同じ道を全く使用しない場合に、本当にコストが下がるのかを確認しましょう。
車1が赤線ルート($Q_{11}$)、車2が緑線ルート($Q_{23}$)を使用しているとき、図からわかるように道の重複は起こっていません。
この時コストの総和は8となり、上の例よりも下がっていることが確認できます。
以上のことを一般化すると、道の重複度(混雑度)を表すコスト関数は以下のようにすれば良さそうです。
$$
\sum_{s \in S}
\left(
\sum_i
\sum_j
\sum_{s \in S_{j}}
Q_{ij}
\right)^2
$$
制約条件(ペナルティー関数)
量子アニーリングは制約式を入れることができないので、制約を破った時に目的関数の値が大きくなるようにペ、制約式をナルティー関数として目的関数の中に入れてしまいます。
今回の制約は車の取るルートは1つのみというものです。そこで先ほどの具体例では以下の式をペナルティー関数とすれば良さそうです。
$$
K・(Q_{11}+Q_{12}+Q_{13}-1)^2-K・(Q_{21}+Q_{22}+Q_{23}-1)^2
$$
ここで、Kはコスト関数とペナルティー関数の重さを調節するハイパーパラメータです。
これを一般化するとペナルティー関数は以下のようになります。
$$
K
\sum_i
\left(
\sum_j
Q_{ij}
-1
\right)^2
$$
よって、目的関数は次のような形になります。
$$
\sum_{s \in S}
\left(
\sum_i
\sum_j
\sum_{s \in S_{j}}
Q_{ij}
\right)^2
+
K
\sum_i
\left(
\sum_j
Q_{ij}
-1
\right)^2
$$
QUBOの行列形式への変形
目的関数を$Q_{ij}$のまま展開すると、$Q_{ij}$に関する2次式となります。よって、行列形式では以下のように書くことができます。

ここで真ん中の行列は$Q_{ij},Q_{i'j'}$の係数となっています。
この行列のアルゴリズム的な作り方は、以下のように行います。
コスト関数の成分
- 道sを使用するルートjを提案されている対角成分に(+1)
- 道路sを使用するルートjを提案されている車$i_{1},i_{2}$の係数成分に(+2)
ペナルティー関数の成分 - 全ての対角成分に(-K)
- $Q_{ij},Q_{ij'}$の係数成分に(+2K)
実験
北京の空港と市内を行き来する418台のタクシーのデータを使い、実際に最適化を行いました。
T-Drive TrajectoryデータベースのGPSデータを用いています。
またそれぞれの車に対して、選択肢として3つのルートが存在するので、解の組み合わせの総数は$3^{418}$通りになります。
QUBOを解き、車を再配置するのを計50回行いました。
また、使用したハードはD-Wave2X QPU(1,152qubit)です。
しかし今回の変数の数が、418台×3ルート=1,254個になるのでbit数が足りません。そこで、qusolvというライブライりを用いて、問題を分割して逐次最適化を行っています。
結果
数値実験を行った結果についてです。
まず計算時間ですが、量子と古典とのやりとりなどのクラウド処理を除いた計算時間は約22秒でした。今回の実験結果を車のルートをランダムに割り当てる場合と比較しています。
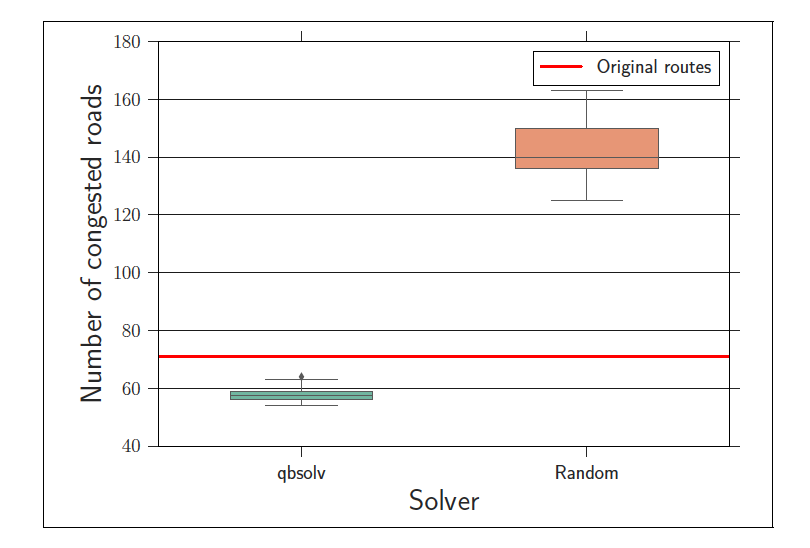
以下が実験結果のランダムとの比較です。縦軸は混雑している道路の数です。
オレンジがランダムにルートを割り当てた場合、赤線が元々存在する混雑道路数、緑が量子アニーリングを用いた結果です。
有意に混雑が改善されていることがわかります。
結果を可視化した図は次のようになります。左が元々のグラフ、右が混雑解消後のグラフです。
考察
「量子アニーリングは実行解が全然出てこない」という話を聞いていたのですが、それが何故かこの論文でよくわかりました。
このハイパーパラメータK(論文中では$\lambda$)の調節が非常に難しいことによると思います。
「量子アニーリングで社会問題を解く」という初期段階の論文なので仕方がないとは思いますが、モデルがかなり現実問題とかけ離れている気がします。
例えば、道の幅などが全く考慮されていない点や、交通流の最適化の目的に対して同じ道路を使う車の台数の最小化のみを行っているなどです。
交通最適化は最適化の分野でも盛んに研究が行われている分野です。その中でもこのようなモデル化はほとんど行われていません。
古典でよく行われているのが、車の流れをひとまとまりに見て流体として表すことです。このようにモデル化することで、解の総数を減らしながらも現実に近いモデルを表すことができたりします。
目的関数についても今回のようにしないで、「目的地までの平均到達時間の最小化」と目的をそのまま直接設定してしまい、解の評価をシミュレーションで行うことが多いです。
このように個別の車に経路を提案するモデル化だと、一定時間ごとに逐次最適経路を提案する、といったものがあります。
また今回の元の地図の混雑を可視化した図を見ると、割当先の道路における車の数を考慮していないように思えます。それら全ての道路の混み具合を考慮したほうが良いと感じました。
しかしながら、量子アニーリングの強みはこのように解の総数が莫大になるような個々の車に着目できることにあると思います。古典的な研究に習って、古典コンピュータによるシミュレーションを同時に行うと面白いのではないかと思いました。車の流れを古典コンピュータでシミュレーションし、ある一定の時間間隔で量子コンピュータで最適化を繰り返します。このように、空いてる道路と混雑している道路を逐次アップデートすることによってより現実に近いことができそうです。
現状のままでは、とても現実社会で使えるようなものではないのでこれからの研究に期待したいです。