運搬経路問題(VRP)を解く 混合整数計画編

ロジスティクス（物流）関連の有名問題を勉強がてらpythonで解いていこうと思い立つ。
ということで、初回は運搬経路問題を整数計画法で解いてみる。

運搬経路問題とは？

英語名Vehicle Routing Problem(VRP)。
ORWiki 運搬経路問題に詳しい説明が記載されている。
簡単に言うと、デポと呼ばれる拠点に所属する運搬車を用い、複数顧客の需要を満たすための最小コストを求める問題である。分かりづらければ、ヤマト宅急便のトラック総運行距離を最小化するように計画を作成すると考えたら良い。（可哀そうに、彼らの場合は不在のための再配送があるので、数理問題に落とし込むのが激難、、というか無理。）
配送を行っている会社は、どこも自動化を目指してシステム導入を目指すけど、完全な自動化はなかなか難しい。突然のオーダ変更やら、サイズの分からない商品などがあるためです。大体の会社は職人がExcelで作成している印象。

問題の種類

• VRPは、下記のような条件の有無で問題が種別される。市場に出ているソフトは大体の制約に対応してる。今回はトラック容量のみを制約として考える。
  • PickUP and Delivery（VRPPD)
    • 積み地が複数。デポ1つではない。
  • LIFO
    • 後入れ・先出し制約。トラックの奥に積んだ荷物を手前の荷物をどけて取り出すのは手間になるため。現実の輸送計画では重要。
  • 時間枠(VRPTW)
    • 顧客ごとの配送希望時間帯制約。
  • トラック容量(CVRP)
    • トラックに容量制約がある

定式化

VRPはNP困難なため、市販ソフトはヒューリスティック解法を採用しています。今回は勉強がてら、MIP(混合整数計画）で解きます。説明はソースの中に。不親切ですいません。pulpというライブラリを使っていますが、よく知らない方はpulpの使い方がいまいちという方のために、以下の記事をリンクします。
PuLP による線型計画問題の解き方ことはじめ
ちなみに、今回はVRPの英語Wikiに紹介されているDFJの拡張版を実装。

ソース

CVRPwithMIP.py

import pulp
import pandas as pd
import numpy as np
import networkx as nx
import itertools
import matplotlib.pyplot as plt
num_client = 15 #顧客数（id=0,1,2,...14と番号が振られていると考える。id=0はデポ。）
capacity = 50　#トラックの容量
randint = np.random.randint

seed = 10
# 各顧客のx,y座標と需要（どのくらいの商品が欲しいか）をDataFrameとして作成
df = pd.DataFrame({"x":randint(0,100,num_client),
                   "y":randint(0,100,num_client),
                   "d":randint(5,40,num_client)})
#0番目の顧客はデポ（拠点）とみなす。なので、需要=0, 可視化の時に真ん中に来るよう、
#x,yを50に。
df.ix[0].x = 50
df.ix[0].y = 50
df.ix[0].d = 0
# costは顧客数✖️顧客数の距離テーブル。np.arrayで保持。
cost = create_cost()
# subtoursはデポ（id=0)を除いた顧客の全部分集合。これがなんの役に立つかは後ほど。
subtours = []
for length in range(2,num_client):
     subtours += itertools.combinations(range(1,num_client),length)

# xは顧客数✖️顧客数のbinary変数Array。Costテーブルと対応している。1ならばその間をトラックが走ることになる。
# num_vは必要なトラック台数変数。
x = np.array([[pulp.LpVariable("{0}_{1}".format(i,j),0,1,"Binary")
               for j in range(num_client)]
              for i in range(num_client)])
num_v = pulp.LpVariable("num_v",0,100,"Integer")

#問題の宣言と目的関数設定。目的関数は、総距離最小化。
problem = pulp.LpProblem('vrp_simple_problem', pulp.LpMinimize)
problem += pulp.lpSum([x[i][j]*cost[i][j]
                       for i in range(num_client)
                      for j in range(num_client)])

# 顧客1から顧客1に移動といった結果は有り得ないので除外
for t in range(num_client):
    problem += x[t][t] == 0

# 顧客から出て行くアーク（トラック）と入っていくアーク（トラック）はそれぞれ必ず１本
for t in range(1,num_client):
    problem += pulp.lpSum(x[:,t]) == 1
    problem += pulp.lpSum(x[t,:]) == 1

# デポ（ここでは、id=0)に入ってくるアーク（トラック）と出て行くアーク（トラック）の本数は必ず一緒。
problem += pulp.lpSum(x[:,0]) == num_v
problem += pulp.lpSum(x[0,:]) == num_v

# ここは肝。上記までの制約だと、デポに戻らない孤立閉路が出来てしまう。ここでやっているのは、
# subtour eliminate制約。さらに、需要も見て、ここでCapacity制約も追加している。興味がある
# 方は、subtour eliminateで検索してください。
for st in subtours:
    arcs = []
    demand = 0
    for s in st:
        demand += df_dpsts["d"][s]
    for i,j in itertools.permutations(st,2):
        arcs.append(x[i][j])
    print(len(st) - np.max([0,np.ceil(demand/capacity)]))
    problem += pulp.lpSum(arcs) <= np.max([0,len(st) - np.ceil(demand/capacity)])

#計算及び結果の確認
status = problem.solve()
print("Status", pulp.LpStatus[status])
for i in range(num_client):
    for j in range(num_client):
        print(i,j,x[i][j].value())

output_image(G,x)

可視化

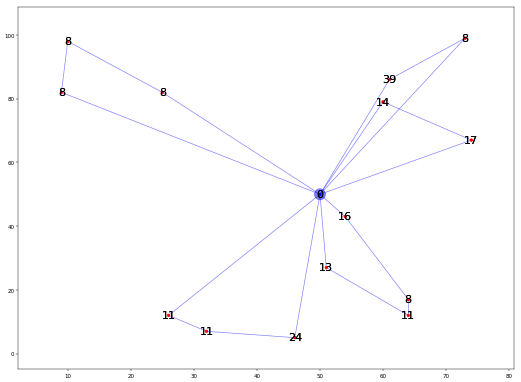
解の可視化。青点がデポで、赤点が顧客（数値は需要。）
トラックは５台必要なことがわかる。それぞれの閉路の総需要がトラックのキャパシティ（=50)を超えていないことに注目。

結論

解けた！上記の定式化は、特にSubtour eliminationの制約数が顧客数と共に爆発的に増えるので、、、あと少し顧客数増えたら解けなくなります。ここらは一工夫あるのですが、今回は紹介せず。
次回はヒューリスティック（厳密解ではないが良い解を求める）な方法を書いてみようかと。