1.5ビットの残差

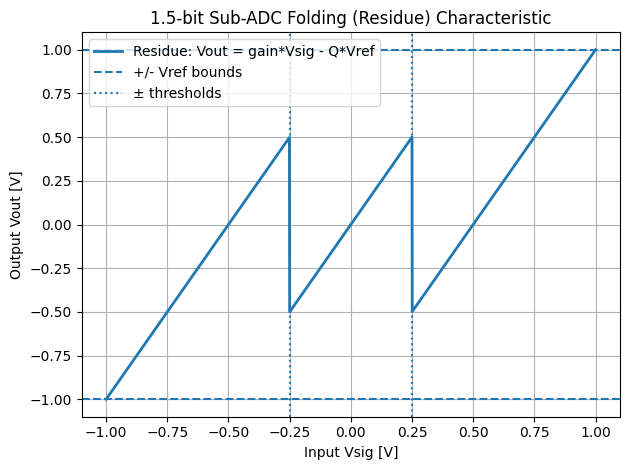
1. 基本式（折り返し残差）

$$
V_{\text{out}} = 2V_{\text{sig}} - Q(V_{\text{sig}}),V_{\text{ref}}
$$

ここで

• $V_{\text{sig}}$：入力信号
• $V_{\text{ref}}$：基準電圧
• $Q(V_{\text{sig}}) \in {-1, 0, +1}$：量子化コード

---

2. 区間ごとの展開

(a) $V_{\text{sig}} < -\frac{V_{\text{ref}}}{4}$ のとき

このとき $Q = -1$。

$$
V_{\text{out}} = 2V_{\text{sig}} - (-1),V_{\text{ref}} = 2V_{\text{sig}} + V_{\text{ref}}
$$

• 出力は傾き 2 の直線で、入力が小さいほど大きく負方向に進む。
• ただしシフト $+V_{\text{ref}}$ があるため、$-V_{\text{ref}}$ で折り返す。

---

(b) $-\frac{V_{\text{ref}}}{4} \leq V_{\text{sig}} \leq +\frac{V_{\text{ref}}}{4}$ のとき

このとき $Q = 0$。

$$
V_{\text{out}} = 2V_{\text{sig}}
$$

• 原点を通る直線、傾きは 2。
• 入力がゼロのとき残差もゼロ。

---

(c) $V_{\text{sig}} > +\frac{V_{\text{ref}}}{4}$ のとき

このとき $Q = +1$。

$$
V_{\text{out}} = 2V_{\text{sig}} - V_{\text{ref}}
$$

• 出力は傾き 2 の直線だが、$-V_{\text{ref}}$ だけシフトされる。
• $,+V_{\text{ref}}$ で折り返す。

---

3. 全体のイメージ

• 各区間で 傾き = 2 の直線 だが、判定に応じて $\pm V_{\text{ref}}$ の補正が入る。
• その結果、入力範囲 $[-V_{\text{ref}}, +V_{\text{ref}}]$ を常に $[-V_{\text{ref}}, +V_{\text{ref}}]$ に収める折り返し波形 となる。
• 図の「ジグザグの青線」はこの式そのものを表している。

---

4. 最終まとめ

$$
V_{\text{out}} =
\begin{cases}
2V_{\text{sig}} + V_{\text{ref}}, & V_{\text{sig}} < -\tfrac{V_{\text{ref}}}{4} \
2V_{\text{sig}}, & -\tfrac{V_{\text{ref}}}{4} \leq V_{\text{sig}} \leq +\tfrac{V_{\text{ref}}}{4} \
2V_{\text{sig}} - V_{\text{ref}}, & V_{\text{sig}} > +\tfrac{V_{\text{ref}}}{4}
\end{cases}
$$

# Program Name: folding_1p5bit.py
# Creation Date: 20250821
# Overview: Simulate a 1.5-bit sub-ADC folding (residue) characteristic and plot Vout versus Vsig, plus a time-domain ramp test.
# Usage: Run this script as-is. Adjust parameters in the "User parameters" section to change Vref, gain, thresholds, sweep range, and ramp settings.

# If needed in notebooks like Colab, uncomment the next line:
# !pip install numpy matplotlib -q

import numpy as np
import matplotlib.pyplot as plt

# =========================
# User parameters / パラメータ一元管理
# =========================

Vref: float = 1.0            # Reference voltage [V] / 基準電圧[V]
gain: float = 2.0            # Interstage gain (folding slope) / 折り返し部の傾き(段間ゲイン)
th_ratio: float = 1.0/4.0    # Threshold ratio (±Vref/4) / しきい値の比率（±Vref/4）
vmin: float = -1.0           # Input sweep min normalized to Vref=1 / 入力最小（Vref=1基準）
vmax: float =  1.0           # Input sweep max normalized to Vref=1 / 入力最大（Vref=1基準）
Npts: int   = 2001           # Number of sweep points / サンプル点数
show_grid: bool = True       # Show grid or not / グリッド表示
linewidth_main: float = 2.0  # Plot line width / 線幅

# Ramp test parameters / ランプ波パラメータ（時間領域テスト）
T_ramp: float = 1.0          # Ramp duration [s] / ランプ継続時間
fs_time: float = 20000.0     # Time sampling rate [Hz] / 時間サンプリング周波数
include_q_trace: bool = True # Plot q*Vref in the time plot / 時間波形に q*Vref も表示

# =========================
# Derived values / 派生値
# =========================

Vth_pos: float =  th_ratio * Vref   # +threshold / 正のしきい値
Vth_neg: float = -th_ratio * Vref   # -threshold / 負のしきい値

# =========================
# Quantizer & residue definitions / 量子化器と残差の定義
# =========================

def q_1p5bit(vsig: np.ndarray, vref: float, vth_pos: float, vth_neg: float) -> np.ndarray:
    """
    1.5-bit 3-level quantizer: returns {-1, 0, +1}
    1.5ビット3値量子化器：{-1, 0, +1} を返す
    """
    q = np.zeros_like(vsig, dtype=np.int8)
    q[vsig >  vth_pos] = +1
    q[vsig <  vth_neg] = -1
    return q

def residue(vsig: np.ndarray, vref: float, gain_: float, q: np.ndarray) -> np.ndarray:
    """
    Folding residue: Vout = gain * Vsig - q * Vref
    折り返し残差：Vout = ゲイン*入力 - 量子化コード*Vref
    """
    return gain_ * vsig - q.astype(float) * vref

# =========================
# Sweep & compute / 掃引して計算（静特性）
# =========================

Vsig = np.linspace(vmin * Vref, vmax * Vref, Npts)   # Input sweep / 入力掃引
Q     = q_1p5bit(Vsig, Vref, Vth_pos, Vth_neg)       # Quantized code / 量子化コード
Vout  = residue(Vsig, Vref, gain, Q)                 # Residue output / 残差出力

# =========================
# Piecewise check (optional) / 区間ごとの検算（任意）
# =========================
# (a) Vsig < -Vref/4 -> Vout = 2*Vsig + Vref
# (b) -Vref/4 <= Vsig <= +Vref/4 -> Vout = 2*Vsig
# (c) Vsig > +Vref/4 -> Vout = 2*Vsig - Vref

# =========================
# Plot 1: Static residue characteristic / 静特性プロット
# =========================

plt.figure()
plt.plot(Vsig, Vout, linewidth=linewidth_main, label="Residue: Vout = gain*Vsig - Q*Vref")
plt.axhline(+Vref, linestyle="--", label="+/- Vref bounds")
plt.axhline(-Vref, linestyle="--")
plt.axvline(+Vth_pos, linestyle=":", label="± thresholds")
plt.axvline( Vth_neg, linestyle=":")
plt.title("1.5-bit Sub-ADC Folding (Residue) Characteristic")
plt.xlabel("Input Vsig [V]")
plt.ylabel("Output Vout [V]")
plt.legend(loc="best")
if show_grid:
    plt.grid(True)
plt.tight_layout()

# =========================
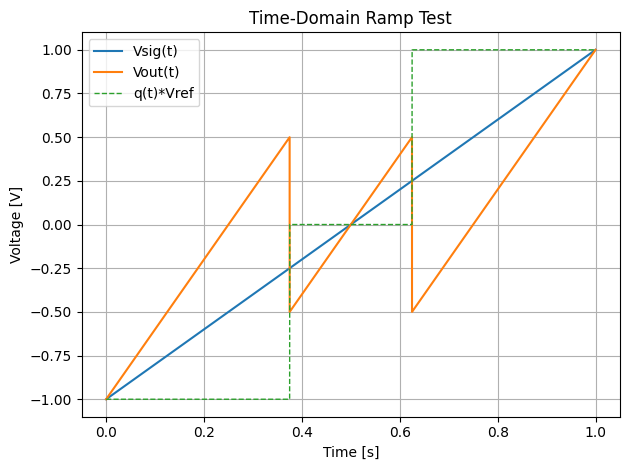
# Time-domain ramp test / 入力ランプ波テスト（時間領域）
# =========================

# Create a single ramp from vmin*Vref to vmax*Vref over T_ramp seconds
t = np.arange(0.0, T_ramp, 1.0/fs_time)
Vsig_ramp = np.linspace(vmin * Vref, vmax * Vref, t.size)

Q_ramp    = q_1p5bit(Vsig_ramp, Vref, Vth_pos, Vth_neg)
Vout_ramp = residue(Vsig_ramp, Vref, gain, Q_ramp)

plt.figure()
plt.plot(t, Vsig_ramp, linewidth=1.5, label="Vsig(t)")
plt.plot(t, Vout_ramp, linewidth=1.5, label="Vout(t)")
if include_q_trace:
    plt.plot(t, Q_ramp.astype(float)*Vref, linewidth=1.0, linestyle="--", label="q(t)*Vref")
plt.title("Time-Domain Ramp Test")
plt.xlabel("Time [s]")
plt.ylabel("Voltage [V]")
plt.legend(loc="best")
if show_grid:
    plt.grid(True)
plt.tight_layout()

plt.show()

# =========================
# Numeric sanity check prints / 数値チェック出力
# =========================

test_points = np.array([vmin*Vref, Vth_neg*1.1, 0.0, Vth_pos*1.1, vmax*Vref])
test_Q = q_1p5bit(test_points, Vref, Vth_pos, Vth_neg)
test_Vout = residue(test_points, Vref, gain, test_Q)
for v, q, r in zip(test_points, test_Q, test_Vout):
    print(f"Vsig={v:+.4f} V, Q={int(q):+d}, Vout={r:+.4f} V")

# End of script