はじめに
SAR ADC(逐次比較型 A/D コンバータ)はシンプルかつ低消費電力なアーキテクチャですが、量子化ノイズやコンパレータノイズが性能を制約します。
これに対して ノイズシェーピング (Noise Shaping) を導入することで、ノイズを高周波に押し上げ、低周波帯域の分解能を改善することが可能です。
本記事では、FIR フィルタと IIR フィルタを組み合わせた FIR-IIR ループフィルタ方式によるノイズシェーピング SAR ADC を解説します。
システム構成
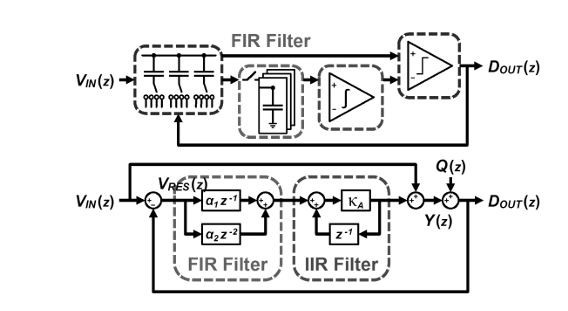
システムは以下のように構成されます:
-
入力信号 $V_{IN}(z)$
SAR ADC に入力されるアナログ信号の離散時間表現。 -
残差電圧 $V_{RES}(z)$
比較器や DAC による逐次近似の過程で生じる誤差信号。 -
FIR フィルタ
- 2タップ構成
- 係数:$\alpha_1, \alpha_2$
- 残差信号を整形し、ゼロ配置を制御する役割を持つ。
-
IIR フィルタ
- 積分器で構成される
- 品質因子(ゲイン)$\kappa_A$ が性能を決定
- ノイズを高周波に押し上げる「シェーピング効果」の中心。
-
量子化器
フィルタ出力 $Y(z)$ と入力信号が加算され、量子化器によりデジタル出力 $D_{OUT}(z)$ が得られる。
数式表現
システム全体の出力は次のように表されます:
$$
D_{OUT}(z) = V_{IN}(z) + \frac{1 - \kappa_A z^{-1}}{1 - \kappa_A (\alpha_1 - 1) z^{-1} + \kappa_A \alpha_2 z^{-2}} Q(z)
$$
ここで:
- $V_{IN}(z)$:入力信号
- $Q(z)$:量子化ノイズ
- $\alpha_1, \alpha_2$:FIR フィルタの係数
- $\kappa_A$:IIR フィルタ(積分器)のパラメータ
ノイズシェーピング効果
この式は 信号伝達関数 (STF) と ノイズ伝達関数 (NTF) に分けて解釈できます:
-
信号伝達関数 (STF)
$$
STF(z) = 1
$$→ 入力信号 $V_{IN}(z)$ は忠実に通過する。
-
ノイズ伝達関数 (NTF)
$$
NTF(z) = \frac{1 - \kappa_A z^{-1}}{1 - \kappa_A (\alpha_1 - 1) z^{-1} + \kappa_A \alpha_2 z^{-2}}
$$→ 量子化ノイズ $Q(z)$ の周波数特性を決定。
→ 分子の $1 - \kappa_A z^{-1}$ によって、**低周波でのノイズ抑圧(ノイズゼロ配置)**が実現される。
FIR/IIR の役割分担
-
FIR フィルタ:
ゼロ配置を調整して 低周波でのノイズ除去性能を制御。 -
IIR フィルタ:
極配置を決め、システムの安定性とノイズシェーピング強度を調整。
これらを組み合わせることで、シンプルな一次ノイズシェーピングに比べて より急峻なノイズスペクトルの減衰が可能になります。
ポイントまとめ
- FIR の係数 $\alpha_1, \alpha_2$ によってゼロ配置を調整し、低周波帯域のノイズを最小化。
- IIR のパラメータ $\kappa_A$ によって極の位置を制御し、ノイズシェーピング効果を強化。
- このハイブリッド方式により、帯域幅と分解能のトレードオフを改善。
- 高分解能・低消費電力 ADC 設計における有力な手法の一つ。
import numpy as np
import matplotlib.pyplot as plt
from scipy.signal import lfilter, freqz
# ==============================
# Parameters
# ==============================
fs = 100e3 # Sampling frequency [Hz]
T = 1/fs # Sampling period [s]
N = 1024 # Number of samples
f_in = 1e3 # Input sine frequency [Hz]
alpha1 = 0.7 # FIR coeff 1
alpha2 = 0.2 # FIR coeff 2
kappaA = 0.9 # IIR integrator quality
# ==============================
# Input signal (sine wave)
# ==============================
n = np.arange(N)
x = np.sin(2*np.pi*f_in*n*T) # Input sine
# ==============================
# Quantization noise (simulate as white noise)
# ==============================
Q = 0.01 * np.random.randn(N)
# ==============================
# Noise Transfer Function (NTF)
# H(z) = (1 - kappaA z^-1) / (1 - kappaA(alpha1-1)z^-1 + kappaA alpha2 z^-2)
# ==============================
b = [1, -kappaA] # Numerator
a = [1, -kappaA*(alpha1-1), kappaA*alpha2] # Denominator
# Filter only the noise path
y_noise = lfilter(b, a, Q)
# Output = input + shaped noise
dout = x + y_noise
# ==============================
# Plot time-domain signals
# ==============================
plt.figure(figsize=(10,5))
plt.plot(n*T*1e3, x, label="Input (sine)")
plt.plot(n*T*1e3, dout, label="Output (signal + shaped noise)", alpha=0.7)
plt.xlabel("Time [ms]")
plt.ylabel("Amplitude")
plt.title("Noise-Shaping SAR ADC (FIR+IIR Feedback)")
plt.grid(True)
plt.legend()
plt.show()
# ==============================
# Plot NTF frequency response
# ==============================
w, h = freqz(b, a, worN=512)
f = w / (2*np.pi) * fs
plt.figure(figsize=(8,5))
plt.semilogx(f, 20*np.log10(abs(h)))
plt.title("Noise Transfer Function (NTF) Frequency Response")
plt.xlabel("Frequency [Hz]")
plt.ylabel("Magnitude [dB]")
plt.grid(True, which="both", ls="--")
plt.show()